Частота найквиста как найти

Частота Найквиста — в цифровой обработке сигналов частота, равная половине частоты дискретизации. Названа в честь Гарри Найквиста.

Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том случае, если (спектральная плотность) наивысшая частота полезного сигнала равна половине или меньше частоты дискретизации (в англоязычной литературе под обозначением половины частоты дискретизации употребляют термин частота Найквиста). В противном случае при восстановлении аналогового сигнала будет иметь место наложение спектральных «хвостов» (подмена частот, маскировка частот, алиасинг), и форма восстановленного сигнала будет искажена. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то сигнал может быть (теоретически) продискретизирован и затем восстановлен без искажений. Фактически «оцифровка» сигнала (превращение аналогового сигнала в цифровой) сопряжена с квантованием отсчётов — каждый отсчёт записывается в виде цифрового кода конечной разрядности, в результате чего к отсчётам добавляются ошибки квантования (округления), при определённых условиях рассматриваемые как «шум квантования».

Реальные сигналы конечной длительности всегда имеют бесконечно широкий спектр, более или менее быстро убывающий с ростом частоты. Поэтому дискретизация сигналов всегда приводит к потерям информации (искажению формы сигнала при дискретизации—восстановлении), как бы ни была высока частота дискретизации. При выбранной частоте дискретизации искажение можно уменьшить, если обеспечить подавление спектральных составляющих аналогового сигнала (до дискретизации), лежащих выше частоты Найквиста, для чего требуется противоподменный фильтр очень высокого порядка, чтобы избежать наложения «хвостов». Практическая реализация такого фильтра весьма сложна, так как амплитудно-частотные характеристики фильтров имеют не прямоугольную, а гладкую форму, и образуется некоторая переходная полоса частот между полосой пропускания и полосой подавления. Поэтому частоту дискретизации выбирают с запасом, к примеру, в аудио компакт-дисках используется частота дискретизации 44100 Герц, в то время как высшей частотой в спектре звуковых сигналов, которую может услышать человек, считается частота 20000 Гц. Запас по частоте Найквиста в 44100 / 2 — 20000 = 2050 Гц позволяет избежать подмены частот при использовании реализуемого фильтра невысокого порядка.

Ссылки[править | править код]

• H. Nyquist, “Certain topics in telegraph transmission theory, ” Trans. AIEE, vol. 47, pp. 617—644, Apr. 1928

Частота
Найквиста —
в цифровой обработке сигналов частота,
равная половине частоты дискретизации.
Названа в честь Гарри Найквиста. Из
теоремы Котельникова следует, что при
дискретизации сигнала полезную информацию
будут нести только частоты ниже частоты
Найквиста. Частоты выше частоты Найквиста
являются зеркальным отображением нижних
частот. Если спектр сигнала не имеет
составляющих выше частоты Найквиста,
то он может быть оцифрован и затем
восстановлен без искажений.

К
примеру, в аудио компакт-дисках
используется частота дискретизации
44100 герц. Частота Найквиста для них —
22050 герц, она ограничивает верхнюю полосу
частот, до которой звук может быть
воспроизведён без искажений.

Но
это – теоретический предел. На практике
есть некоторые нюансы. При оцифровке
аналогового сигнала с широким спектром
необходимо обеспечить срез спектра
аналогового сигнала на частоте Найквиста
при помощи фильтра очень высокого
порядка, чтобы избежать зеркального
отражения спектра для частот, лежащих
выше частоты Найквиста. Практическая
реализация такого фильтра весьма сложна,
так как амплитудно-частотные характеристики
фильтров имеют не прямоугольную, а
колоколообразную форму и образуется
некоторая полоса “затухания”.
Поэтому максимальную частоту спектра
дискретизуемого сигнала принимают
несколько ниже частоты Найквиста, чтобы
обеспечить надёжное подавление фильтром
спектра дискретизуемого сигнала.

Теоре́ма
Коте́льникова
(в англоязычной
литературе — теорема Найквиста —
Шеннона или теорема отсчётов) гласит,
что, если аналоговый сигнал

имеет ограниченный спектр, то он может
быть восстановлен однозначно и без
потерь по своим дискретным отсчётам,
взятым с частотой строго большей
удвоенной максимальной частоты спектра
:

где
—
-верхняя
частота в спектре, или (формулируя
по-другому) по отсчётам, взятым с периодом
, чаще полупериода максимальной частоты
спектра
:

Пояснение

Такая
трактовка рассматривает идеальный
случай, когда сигнал начался бесконечно
давно и никогда не закончится, а также
не имеет во временно́й характеристике
точек разрыва. Именно это подразумевает
понятие «спектр, ограниченный частотой
».

Разумеется,
реальные сигналы (например, звук на
цифровом носителе) не обладают такими
свойствами, так как они конечны по
времени и, обычно, имеют во временно́й
характеристике разрывы. Соответственно,
их спектр бесконечен. В таком случае
полное восстановление сигнала невозможно
и из теоремы Котельникова вытекают 2
следствия:

Любой
аналоговый сигнал может быть восстановлен
с какой угодно точностью по своим
дискретным отсчётам, взятым с частотой
,
где
—
максимальная частота, которой ограничен
спектр реального сигнала.

Если
максимальная частота в сигнале превышает
половину частоты дискретизации, то
способа восстановить сигнал из дискретного
в аналоговый без искажений не существует.

Говоря
шире, теорема Котельникова утверждает,
что непрерывный сигнал
можно представить в виде интерполяционного
ряда

где

—
функция sinc. Интервал дискретизации
удовлетворяет ограничениям
Мгновенные значения данного ряда есть
дискретные отсчёты сигнала
.

стория
открытия

Хотя
в западной литературе теорема часто
называется теоремой Найквиста со ссылкой
на работу 1928 года «Certain topics in telegraph
transmission theory», в этой работе речь идёт
лишь о требуемой полосе линии связи для
передачи импульсного сигнала (частота
следования должна быть меньше удвоеной
полосы). Таким образом, в контексте
теоремы отсчётов справедливо говорить
лишь о частоте Найквиста. Примерно в
это же время Карл Купфмюллер получил
тот же результат.[1] О возможности полной
реконструкции исходного сигнала по
дискретным отсчётам в этих работах речь
не идёт. Теорема была предложена и
доказана В. А. Котельниковым в 1933 году
в работе «О пропускной способности
эфира и проволоки в электросвязи», в
которой, в частности, была сформулирована
одна из теорем следующим образом[2][3]:
«Любую функцию f(t), состоящую из частот
от 0 до fc, можно непрерывно передавать
с любой точностью при помощи чисел,
следующих друг за другом через секунд».
Независимо от него эту теорему в 1949
(через 16 лет!) году доказал Клод Шеннон[4],
поэтому в Западной литературе эту
теорему часто называют теоремой Шеннона.
В 1999 году Международный научный фонд
Эдуарда Рейна (Германия) признал приоритет
В. А. Котельникова, наградив его премией
в номинации «за фундаментальные
исследования» за впервые математически
точно сформулированную и доказанную в
аспекте коммуникационных технологий
теорему отсчётов.[5] Исторические
разыскания показывают, однако, что
теорема отсчётов как в части утверждения
возможности реконструкции аналогового
сигнала по дискретным отсчётам, так и
в части способа реконструкции,
рассматривалась в математическом плане
многими учеными и ранее. В частности,
первая часть была сформулирована ещё
в 1897 году Борелем.[6]

Соседние файлы в папке лекции

• #
• #
• #
• #
• #
• #

The theoretical minimal sampling rate at which a finite bandwidth signal can be sampled to retain all information and reconstructed from its sample without any distortion is called the Nyquist sampling rate (f_n). The other term for the Nyquist rate is the minimum sampling rate. That means when the sampling rate becomes exactly equal to 2f_m samples per second then is called as Nyquist sampling rate. For a bandwidth of span C, the Nyquist frequency is just 2C.

The significance of the Nyquist rate is that it helps to avoid the aliasing problem which is the overlapping of two signals.

Nyquist Rate, f_{n = 2fm}

Where f_m is the maximum frequency component that is present in the signal.

1. If the signal is sampled at a rate greater than Nyquist rate (f_n) then the signal is known as oversampled.
2. If the signal is sampled at a rate less than Nyquist rate (f_n) then the signal is known as under-sampled.

Nyquist Interval

The maximum sampling interval is called the Nyquist interval. That means the rate of sampling is equal to the Nyquist rate, then the time interval between any two adjacent samples is represented as the Nyquist interval. The Nyquist interval can be represented by,

  1/f_n=1/2fm

Now to determine the Nyquist rate and Nyquist interval for the following signal.

x(t)=(2000πt) + 3sin(6000πt) + 8cos(12000πt)

Nyquist Rate:

Now, we have to find the three frequencies:

Highest frequency component in term 2000πt = ω_m1t  is  2000π

fm = ωm1/2π
  = 2000π/2π
  = 1000 hz

  The highest frequency component in the term sin 6000πt = ω_m2t  is  6000π

fm = ωm2/2π
  = 6000π/2π
  = 3000 hz

 The highest frequency component in the term cos 12000πt =ω_m3t  is  12000π

fm = ωm3/2π
  = 12000π/2π
  = 6000 hz

Therefore, the maximum frequency component present in the signal is 6000 hz. Thus, the minimum sampling rate to avoid aliasing i.e., Nyquist rate is  f_n= 2f_m

 = 2 × 6000 hz
 = 12000 hz

 Nyquist interval                                

Now, the Nyquist interval is = 1/f_n

=  1/12000
=   8.3 sec

Last Updated :
16 Feb, 2023

Like Article

Save Article

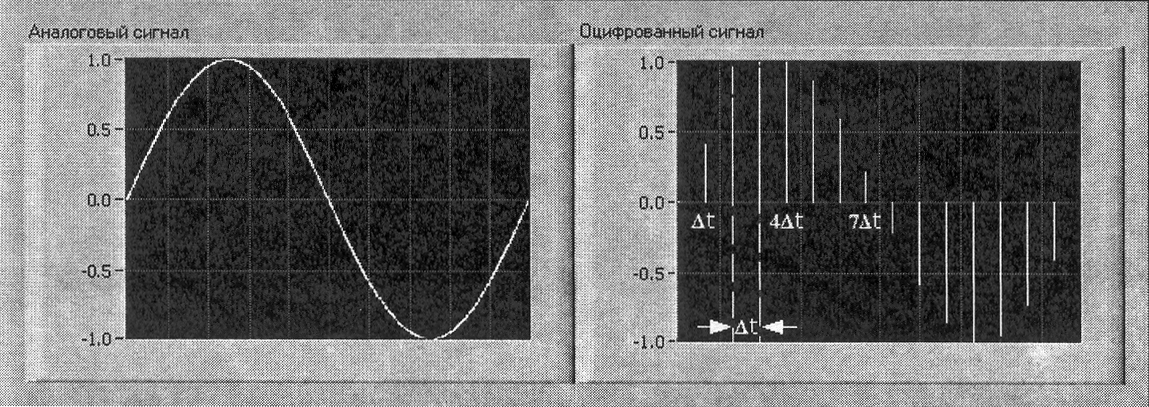
Аналоговый ввод Аналоговое и цифровое представление сигнала 4. Аналоговый ввод Цифровая обработка сигналов обладает многими преимуществами. В связи с этим перед обработкой в компьютере аналоговые сигналы преобразуются в цифровую форму. Цифровым сигналом называется такой сигнал, который может принимать ограниченный ряд значений зависимых и независимых переменных. Независимыми переменными обычно являются время или координаты, а зависимыми – амплитуда. Цифровые (дискретные) сигналы окружают нас повсюду. Телефонные компании используют цифровые сигналы для представления человеческого голоса. Радио, телевизионные и высококачественные звуковые системы – все используют поэтапное преобразование сигнала в цифровую форму из-за ее безукоризненной точности воспроизведения, подавления шумов и больших возможностей обработки сигналов. Снимки NASA удаленных планет и космического пространства часто подвергаются цифровой обработке для удаления шумов и выделения полезной информации. Данные в экономической области, результаты переписи населения и цены акций на фондовой бирже – все это доступно в цифровом виде. Дискретизация сигналов Для получения аналогового сигнала вы, прежде всего, должны преобразовать его в дискретное представление. На практике под этим понимается использование аналого- цифрового преобразователя (АЦП). Рассмотрим аналоговый сигнал х(t), который дискретизируется каждые t секунд. Временной интервал t называют интервалом дискретизации или периодом дискретизации. Обратная величина, 1/t, известна как частота дискретизации или частота выборки с единицей измерения – количество выборок в секунду. Каждое из дискретных значений x(t) в моменты времени t = 0, t, 2t, 3t и т.д. называются выборками. Таким образом, х(0), x(t), х(2t), … образуют полный набор выборок. Сигнал х(t) может быть представлен дискретным набором выборок, как это показано в следующем уравнении: {x(0), х(t), x(2t), x(3t), …,x(kt), …} Следующий рисунок демонстрирует аналоговый сигнал и соответствующую ему оцифрованную версию. Выборки заданы в дискретные моменты времени. 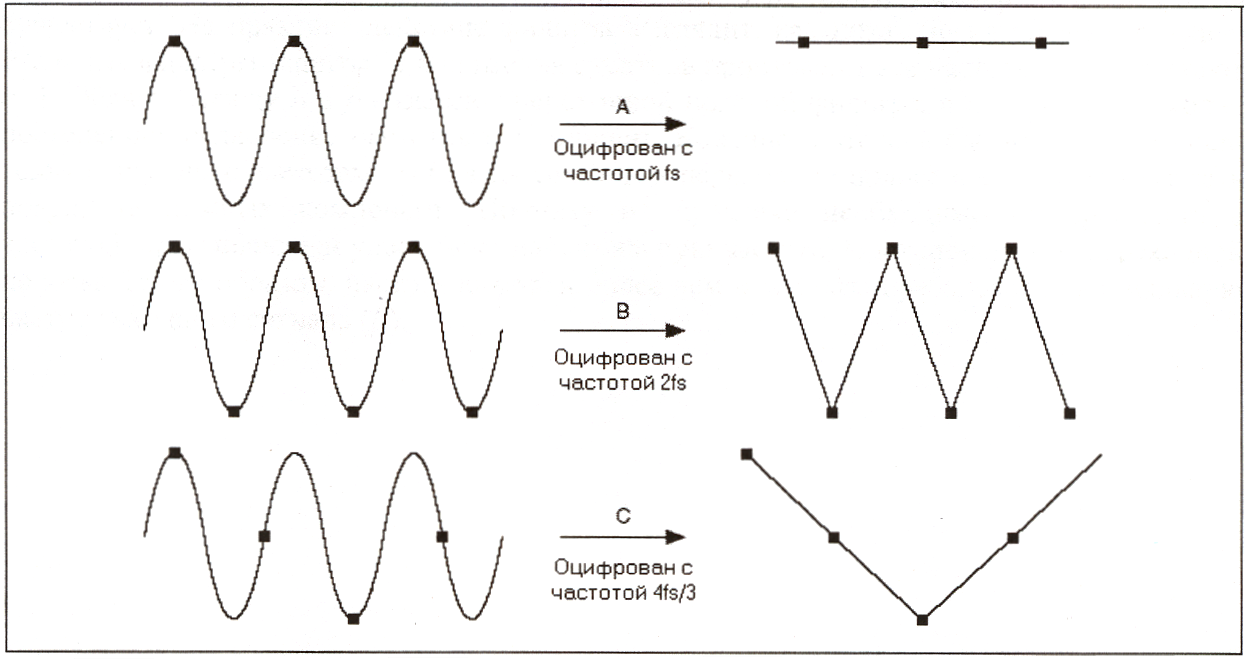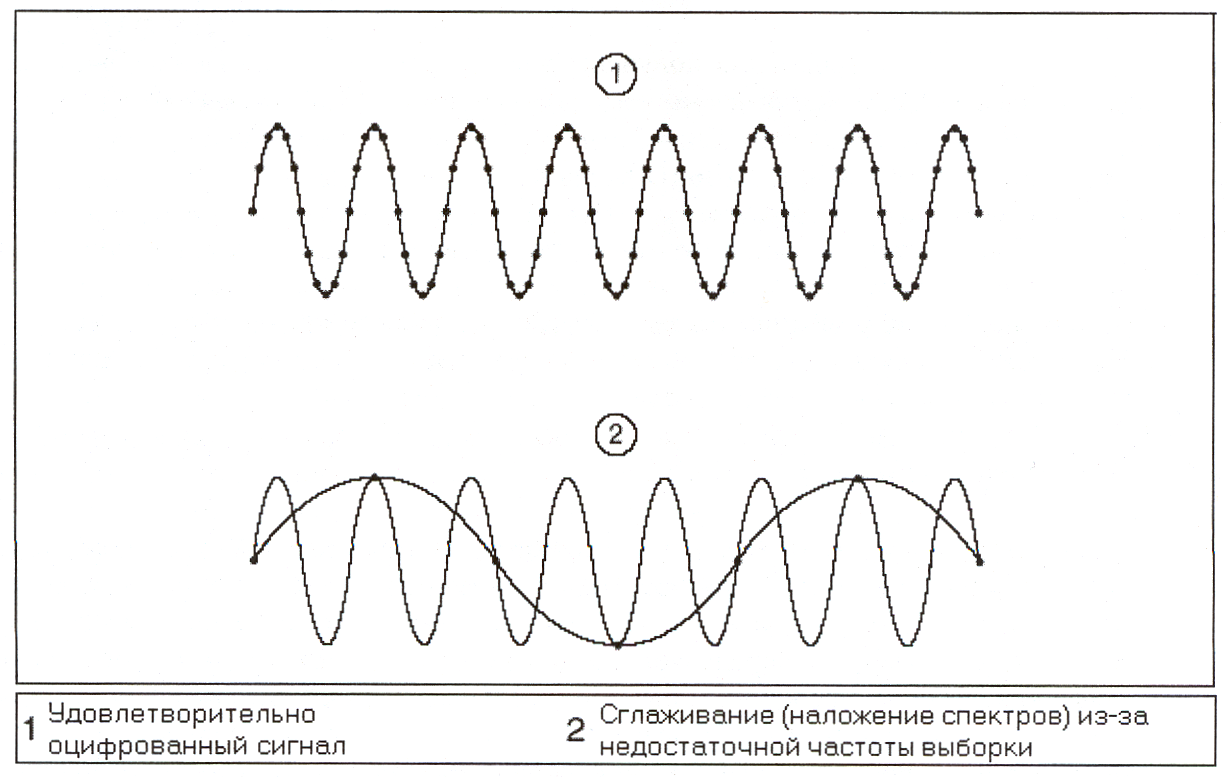Частота выборки Один из наиболее важных параметров измерительной системы с аналоговым вводом или выводом является частота, с которой измерительное устройство производит выборку входного сигнала или генерацию выходного. Частота сканирования или частота выборки в АЦП определяет, насколько часто имеет место аналого-цифровое или цифро-аналоговое преобразование. При большей частоте выборки собирается больше точек за данное время, что позволяет построить лучшее представление исходного сигнала, чем при низкой частоте выборки. Генерация одногерцового сигнала с использованием 1000 точек на период при частоте 1000 выборок в секунду создает гораздо более точное представление, чем использование 10 точек на период при частоте 10 Выб/сек. Наложение частот Слишком низкая частота выборки приводит к такому явлению, как наложение частот (aliasing), что вызывает искажение в представлении аналогового сигнала. Недостаточная скорость оцифровки является причиной того, что сигнал выглядит так, как будто его частота отлична от действительной. Чтобы избежать наложения частот оцифровку производят с частотой, большей частоты самого сигнала. Следующая иллюстрация показывает удовлетворительно оцифрованный сигнал и эффект наложения частот из-за недостаточной частоты выборки. Для точного представления частоты сигнала при измерениях вы должны производить выборки с частотой, большей удвоенной максимальной частотной компоненты сигнала, в соответствии с теоремой Найквиста. Частота Найквиста – это максимальная частота сигнала, при которой его можно точно представить без эффекта наложения частот с данной частотой выборки. Частота Найквиста равна половине частоты выборки. В сигналах, имеющих частотные компоненты, превышающие частоту Найквиста, появятся ложные низкочастотные составляющие. Частота этой составляющей равна по модулю разности между частотой входного сигнала и наиболее близкой частотой, равной целому числу, умноженному на частоту выборки. Например, положим, что частота выборки fs равна 100 Гц. Предположим также, что входной сигнал содержит компоненты с частотами: 25 Гц, 70 Гц, 160 Гц и 510 Гц, как показано на следующем рисунке. 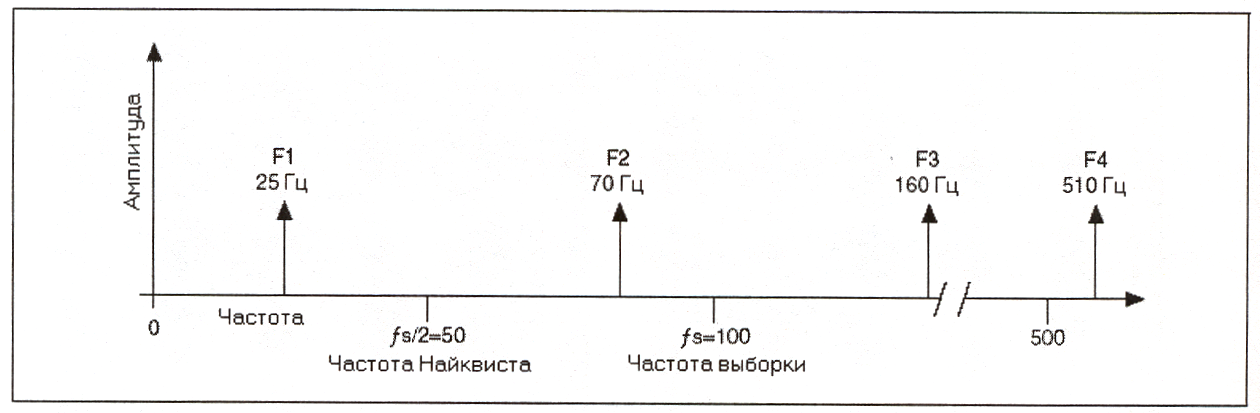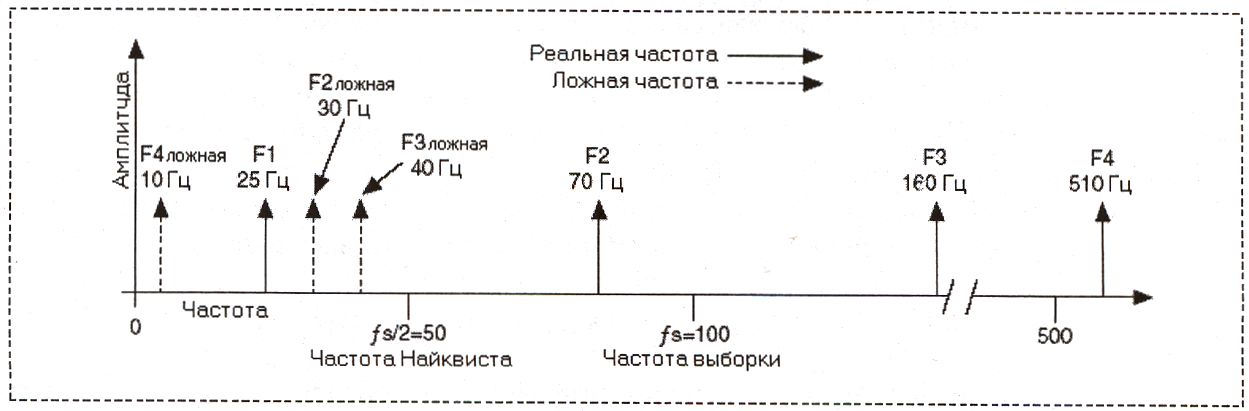Частотные компоненты ниже частоты Найквиста (fs/2 = 50 Гц) оцифровываются правильно. Это показано на следующей иллюстрации. Частотные компоненты выше частоты Найквиста появляются как побочные. Например, F1 (25 Гц) появляется на правильной частоте, a F2 (70 Гц), F3 (160 Гц) и F4 (510 Гц) имеют низкочастотные ложные компоненты на частотах 30 Гц, 40 Гц и 10 Гц, соответственно. Для вычисления ложных частот используйте следующее выражение: Ложная частота = Абсолютное значение (Наиболее близкая частота, равная целому числу, умноженному на частоту выборки – Частота входного сигнала). Например, ложная F2 = |100 – 70| = 30 Гц; ложная F3 = |(2) 100 – 160| = 40 Гц; ложная F4 = |(5)100 – 510| = 10 Гц. Определение частоты выборки Возможно, вы захотите осуществлять выборку с максимально возможной частотой для данного измерительного устройства. Однако если вы оцифровываете очень быстро в течение длительных промежутков времени, то вам может не хватить оперативной памяти или дискового пространства для накопления данных. Следующая иллюстрация показывает влияние различных частот оцифровки на принимаемый сигнал. Пример А: оцифровка синусоидального сигнала частотой f и с такой же частотой дискретизации fs. В результате, полученные выборки образуют постоянный сигнал. Однако если вы увеличите частоту оцифровки до 2fs, то оцифрованная осциллограмма будет иметь ту же частоту (или то же количество циклов), что и исходная осциллограмма, но будет выглядеть как треугольный сигнал, что показано на Примере В. Значительно увеличивая частоту дискретизации по сравнению с fs, вы можете более точно воспроизвести осциллограмму. В Примере С частота выборки равна 4fs/3. Поскольку в этом случае частота Найквиста меньше fs, (4fs/3 х 1)/2 = 2fs/3), то будет воспроизводиться осциллограмма с неправильной частотой и формой. Теорема Найквиста является отправной точкой при выборе достаточной частоты выборки – она должна в два раза превышать максимальную частотную компоненту в сигнале. К сожалению, этой частоты обычно не хватает для практических целей. Сигналы, встречающиеся в реальных приложениях, часто содержат составляющие, лежащие выше частоты Найквиста. Это приводит к добавлению ложных компонент в точно оцифрованный сигнал, что создает искаженные цифровые данные. Поэтому, на практике, выборку производят с частотой, многократно превышающей частоту входного сигнала. Для промышленных приложений является обычным превышение в 5-10 раз.

Смотреть видео >>> Смотреть всё видео

Алиасинг при дискретизации сигналов

Содержание

Обнаружили ошибку?
Выделите ее мышью
и нажмите

Вводные замечания

В предыдущих параграфах мы неоднократно говорили, что при дискретизации аналогового сигнала  происходит бесконечное периодическое копирование спектральной плотности сигнала  c периодом, равным частоте дискретизации  рад/с.

Тогда спектральная плотность  дискретного сигнала

принимает вид:

(1)

В результате,  становится периодической функцией частоты , и при соблюдении условий теоремы Котельникова, копии  не перекрываются, что дает возможность произвести восстановление исходного аналогового сигнала  по дискретному . Однако в общем случае, в результате копирования   по частоте, может наблюдаться эффект наложения спектра сигнала, который носит название алиасинга [1, стр. 197].

В данном разделе мы проанализируем данный эффект и рассмотрим пути подавления алиасинга при дискретизации сигналов.

Частотные зоны Найквиста

Ввиду того, что спектральная плотность  после дискретизации становится периодической, с периодом равным  рад/с, мы можем разбить ось частот на зоны шириной  как это показано на рисунке 1

Рисунок 1. Разбиение оси частот на зоны Найквиста

Частотные зоны, обозначенные римскими цифрами, разделяют ось частот  на полосы шириной  рад/с симметрично относительно нулевой частоты. В результате суммарная ширина каждой зоны равна частоте дискретизации , так как каждая зона состоит из полосы  как в положительной, так и в отрицательной полуоси частот.

Частотные зоны, показанные на рисунке 1, носят название зон Найквиста. При этом выделяют первую зону Найквиста, занимающую полосу  рад/с, а также высшие зоны: вторую, третью и т.д.

Частота , отделяющая границу первой зоны называется частотой Найквиста [2, стр. 169].

Дискретизация сигнала из высших зон Найквиста

Пусть исходный вещественный сигнал  имеет спектральную плотность , расположенную в одной из высших зон Найквиста, как это показано на рисунке 2а.

Рисунок 2. Дискретизация сигнала из третьей зоны Найвиста:
а — Спектральная плотность исходного сигнала;
б — Спектральная плотность дискретного сигнала

Тогда при копировании , в соответствии с (1), спектральная плотность дискретного сигнала  будет иметь вид, как это показано на рисунке 2б.

Можно видеть, что при дискретизации сигнала, спектральные компоненты  «размножаются» во все зоны Найквиста, в результате сигнал из высшей зоны (заштрихованные компоненты) отображается в первую зону. Такое «просачивание» сигнала из высшей зоны Найквиста в первую зону называется эффектом наложения [2, стр. 168], или алиасингом[1] [1, стр. 197].

Важно отметить, что по дискретному сигналу невозможно определить из какой зоны Найквиста исходный аналоговый сигнал был дискретизирован.

Если исходный аналоговый сигнал  будет представлен сразу в нескольких зонах Найквиста, то при дискретизации произойдет смешение спектральных компонент сигнала, как это показано на рисунке 3

Рисунок 3. Дискретизация сигнала, представленного
в нескольких зонах Найвиста:
а — Спектральная плотность исходного сигнала;
б — Спектральная плотность дискретного сигнала

Спектральная плотность  входного аналогового сигнала  представлена в первой и третьей зонах одновременно (рисунок 3а). Тогда на выходе АЦП мы будем иметь дискретный сигнал, чья спектральная плотность  показана на рисунке 3б. Копии спектральной плотности  из третье зоны Найквиста смешиваются с сигналом в первой зоне, и мы не сможем их разделить в цифровой области.

Разумеется, последний пример не выполняет условий теоремы Котельникова, в результате чего алиасинг вносит неустранимые искажения в дискретный сигнал на выходе АЦП. В большинстве случаев алиасинг вреден и требуется применять методы для его устранения при дискретизации сигналов.

Использование аналогового фильтра для устранения алиасинга на выходе АЦП

Подавить алиасинг на выходе АЦП можно при помощи аналогового ФНЧ с частотй среза равной частоте Найквиста (половине частоты дискретизации), как это показано на рисунке 4.

Рисунок 4. Подавление алиасинга на выходе АЦП при помощи ФНЧ

На верхнем графике показана спектральная плотность исходного сигнала (как на рисунке 3), содержащая компоненты в первой и третьей зонах Найквиста. Также показана АЧХ аналогового ФНЧ, который пропускает только сигнал в первой зоне Наквиста и подавляет сигнал во всех высших зонах. В результате вход АЦП не будет содержать компонент из высших зон Найквиста и на выходе АЦП алиасинг не будет наблюдаться.

Таким образом, ФНЧ перед АЦП призван гарантировать соблюдение условий теоремы Котельникова при дискретизации сигнала.

Разумеется, реальные ФНЧ не могут обеспечить полного подавления в полосе заграждения, но могут обеспечить подавление до заданного уровня, например до уровня шумов АЦП. При этом будут наблюдаться незначительные искажения сигнала в полосе пропускания ФНЧ в первой зоне Найквиста. Допустимый уровень искажений в полосе пропускания должны быть заданы при проектировании ФНЧ.

Демонстрация алиасинга во временно́й области

В предыдущих параграфах мы рассмотрели эффект алиасинга в частотной области, возникающий в результате копирования спектральной плотности  при дискретизации сигнала. В данном параграфе мы покажем эффект алиасинга во временно́й области.

Пусть исходный сигнал  имеет вид (см. рисунок 5а):

(2)

Спектральная плотность 

(3)

сигнала (2) показана на рисунке 5б. Пунктирная линия означает чисто мнимую спектральную плотность .

Возьмем дискретные отсчеты сигнала (2) с периодом  с. Тогда частота дискретизации  Гц, или  рад/с. Частота Найквиста равна половине частоты дискретизации, т.е.  рад/с.

Рисунок 5. Алиасинг во временно́й области
a — исходный сигнал во второй зоне Найквиста;
б — спектральная плотность исходного сигнала
в — дискретный сигнал на частоте  рад/с;
г — Спектральная плотность дискретного сигнала.

Поскольку сигнал  находится во второй зоне Найквиста, то при дискретизации мы будем иметь алиасинг, как это показано на рисунке 5в, и спектральная плотность будет иметь вид, показанный на рисунке 5г. Из рисунка 5г видно, что в первой зоне Найвиста появились компоненты на частотах  рад/с. Во временно́й области это огибающая на частоте   рад/с, причем по дискретному сигналу непонятно в какой зоне Найквиста находится исходный сигнал.

Дискретизации гармонических сигналов на границах зон Найквиста

В конце данного раздела рассмотрим любопытный эффект, возникающий при дискретизации гармонического сигнала, расположенного на границе зон Найквиста (если частота дискретизации точно равна удвоенной частоте сигнала ).

Пусть дано два сигнала  и . Продискретизируем оба сигнала с частотой дискретизации  рад/с (интервал дискретизации  с), как это показано на рисунке 6.

Рисунок 6. Дискретизация гармонических
сигналов на границе зон Найквиста:
a — сигнал ; б — сигнал .

Можно видеть, что дискретизация сигнала  произведена в точках максимума и минимума и аналоговый сигнал  может быть полностью восстановлен. Сигнал  дискретизирован в нулях, в результате, все отсчеты данного сигнала равны нулю и сигнал полностью потерян.

Чтобы понять данный эффект необходимо вновь обратиться к (1), а также вспомнить

выражения для спектральных плотностей  и  сигналов  и 

соответственно

(4)

При дискретизации сигналов  и , их спектральный плотности  и  будут копированы с периодом  рад/c и сложены со своими частотными копиями как это показано на рисунке 7.

Рисунок 7. Спектральные плотности
при дискретизации сигналов на границе зон Найквиста:
a — сигнал ; б — сигнал .

Тогда при дискретизации сигнала , копии спектральной плотности  будут попадать строго на одни и те же частоты и при сложении удвоятся. Используя идеальный фильтр нижних частот с АЧХ вида , мы можем восстановить исходный сигнал[2].

Для сигнала  копии  также попадают на одни и те же частоты, но при сложении взаимно уничтожаются, потому что имеют различные знаки. В результате спектральная плотность дискретного сигнала  становится тождественно равна нулю, что мы и видим во временной области.

Дискуссия

Приведенный пример демонстрирует эффект который возникает при попадании сигнала на границу зон Найквиста. Часто при формулировке теоремы Котельникова говорят [3, 4], что частота дискретизации должна быть больше или равна удвоенной верхней частоте сигнала. Такая формулировка неточна, так как не учитывает приведенный граничный эффект. Поэтому правильнее говорить, что частота дискретизации должна быть строго больше верхней частоты сигнала для исключения граничных эффектов. И тут, необходимо отметить, что термин верхняя частота также видится не вполне корректным. И вот почему.

Рассмотрим сигнал , где  рад/c, или проще говоря, частота гармонического сигнала равна 1 МГц. Тогда если руководствоваться понятием верхней частоты, что для представления данного сигнала необходима частота дискретизации больше 2 МГц. С другой стороны полоса самого сигнала  равна нулю, а это значит, что сам гармонический сигнал может быть описан всего тремя числами: амплитудой, начальной фазой и частотой. Но если отталкиваться от верхней частоты, то для его описания требуется более 2 миллионов отсчетов каждую секунду. Если мы увеличим частоту до 1 ГГц, то потребуется уже более 2 миллиардов отсчетов каждую секунду, в то время как мы лишь однократно изменили одно число, описывающее частоту колебания.

Таким образом, «синусоида» не несет никакой информации. Чтобы передавать информацию одной «синусоиды» недостаточно, необходимо какой-то параметр из трех менять во времени. Этот процесс мы называем модуляцией. Модуляция приводит к тому, что полоса модулированного сигнала уже не будет нулевой и станет зависеть от полосы модулирующего сигнала. При этом оказывается, что имея сигнал полосой , неважно на какой несущей частоте, мы можем всю полезную информацию получить при дискретизации данного сигнала с частотой, большей или равной данной полосе. Такой метод дискретизации носит название субдискретизации (или полосовая дискретизация), и он основан на доказанной В.А. Котельниковым теореме, которая в работе [5] обозначена как теорема 5.

В таком подходе термин верхняя частота перестает играть роль. Важна полоса сигнала, потому что она определяет количество информации в сигнале. Если вернуться к

теореме Котельникова,

то она
была изначально сформулирована в терминах полосы  видеосигнала, причем мы требовали чтобы  для исключения эффекта дискретизации на границах зоны Найквиста.

Если продолжать рассуждения, то можно пойти еще дальше, и не использовать полосу, а ставить частоту дискретизации напрямую в зависимость от количества информации в сигнале. Именно такой подход лег в основу техники дискретизации, которая носит название compressed sensing [6, 7] и является неким гибридным методом одновременной дискретизации и сжатия данных с возможностью полного восстановления и сокращения частоты отсчетов.

Выводы

В данном разделе мы рассмотрели эффект алиасинга, возникающий при дискретизации аналоговых сигналов, если не соблюдать условия теоремы Котельникова.

Мы ввели понятие зон Найквиста и показали, что при дискретизации сигналов, представленных в нескольких зонах Найквиста наблюдается смешение частотных компонент на выходе дискретизатора.

Также мы рассмотрели использование аналогового фильтра для ограничении полосы сигнала при дискретизации для устранения
эффекта алиасинга.

Алисаинг был продемонстрирован как во временной, так и в частотной областях.

В конце раздела мы продемонстрировали и пояснили краевой эффект при дискретизации гармонических сигналов на границе зон Найквиста.

Смотри также

Аналоговые, дискретные и цифровые сигналы
Теорема Котельникова

Примечания

[1] от англ. alias (псевдоним)

[2] Заметим, что мы в параграфе

«Спектральная плотность прямоугольного импульса»

доопределили функцию прямоугольного импульса в момент скачка до величины . В результате при прохождении дискретного сигнала через такой фильтр удвоенные компоненты на частотах  будут снова уменьшены в два раза.

Список литературы

[1]

The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

[2]

Оппенгейм А., Шаффер Р.
Цифровая обработка сигналов.
Москва, Техносфера, 2012. 1048 с. ISBN 978-5-94836-329-5

[3]

Баскаков, С.И.
Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[4]

Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.

[5]

Котельников В.А.
О пропускной способности эфира и проволоки в электросвязи.
Материалы к 1 Всесоюзному съезду по вопросам технической реконструкции дела связи и развития слаботочной промышленности,1933, Всесоюзный энергетический комитет.

[6]

Donoho, D., Vetterli, M., DeVore, R.A., Daubechies, I.
Data Compression and Harmonic Analysis
//IEEE TRANSACTIONS ON INFORMATION THEORY, Oct. 1998, №6, Vol. 44, pp 2435-2476.

[7]

Donoho, D.
Compressed Sensing
//IEEE TRANSACTIONS ON INFORMATION THEORY, Apr. 2006, №4, Vol. 52, pp. 1289-1305.

[8]

Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.

Последнее изменение страницы: 12.05.2022 (19:41:38)

Страница создана Latex to HTML translator ver. 5.20.11.14