Частота основного тона как найти

Для школьников.

Механические колебания тела и создаваемые ими волны частот от 16 Гц до 20 кГц, воспринимаемые человеческим ухом, называются звуковыми колебаниями и волнами.

Мы с удовольствием слушаем песню, игру пианиста или скрипача, духовой оркестр. Все эти звуки мы называем музыкальными звуками или музыкой. Другие звуки в виде визга, скрежета, грохота нам неприятны.

В науке музыкальным называется тот звук, в котором изменение акустического давления, воспринимаемого ухом, упорядочено и, кроме того, повторяется регулярно, через равные промежутки времени.

Звук перестаёт быть музыкальным, и его называют шумом, если звуковое давление изменяется в нём беспорядочно.

В каждом музыкальном звуке есть тон и тембр. Понятие звуковой тон ввёл в акустику Галилео Галилей.

Тон звука определяется частотой, с которой изменяется давление в звуковой волне. Низкая частота колебаний соответствует низкому тону, высокая частота колебаний соответствует высокому тону.

Если бы вибрирующие тела в каждый момент времени создавали только один тон, то мы не смогли бы отличить голос одного человека от голоса другого человека, а все музыкальные инструменты звучали бы для нас одинаково.

Всякое вибрирующее тело создаёт одновременно звуки нескольких тонов и при этом различной силы. Самый низкий из них называют основным тоном. Более высокие тона, сопровождающими основной, называют обертонами.

В совместном звучании основной тон и обертоны создают тембр звука.

Если этот процесс изображается синусоидой (является гармоническим), то тон называется простым или чистым. Источником простого (чистого) тона является, например, камертон.

Тон звука определяется частотой, с которой изменяется давление в звуковой волне. Низкая частота колебаний соответствует низкому тону, высокая частота колебаний – высокому тону.

Каждому музыкальному инструменту, каждому человеческому голосу присущ свой тембр, своя “окраска” звука.

Один тембр отличается от другого числом и силой обертонов. Чем больше обертонов в звучании основного тона, тем приятнее тембр звука.

Ухо человека способно анализировать звук (разбираться в совокупности тонов и обертонов), что позволяет ему отличить один тембр от другого.

Если высокие обертоны преобладают в человеческом голосе над низкими, то говорят, что в голосе слышится звучание металла. Когда же преобладают низкие обертоны, то голос называют мягким, бархатистым.

В музыкальных произведениях (симфониях, концертах) одновременно звучит не один тон, а несколько, и каждый из них сопровождается своими обертонами. Такое явление называется созвучием.

Самое простое созвучие – одновременное звучание двух тонов. У каждого из них своя частота колебаний. Отношение двух таких тонов называют интервалом. Если это отношение равно 1:1, то интервал будет унисоном, если отношение 1:2, то – октавой.

Теперь посмотрим на возможные звуковые колебания с точки зрения физики.

При изучении колебаний мы говорили, что самым простым видом колебаний являются гармонические колебания, графически изображаемые синусоидой. Такие колебания характеризуются частотой.

Источником гармонических звуковых колебаний является камертон. Чем короче ножка камертона, тем более высокий звук он излучает при колебании.

Музыкальные же инструменты издают сложные (негармонические) периодические звуковые колебания, имеющие период колебаний, но не имеющие определённой частоты.

На рисунке ниже показаны такие сложные периодические звуковые колебания, излучаемые разными инструментами (кларнетом, пианино и скрипкой).

Видим, что период этих сложных колебаний одинаков, а их вид (форма) разные. Вид колебаний зависит от материала и формы звучащего тела, от резонатора, которым служит корпус инструмента и др.

Согласно теореме Фурье сложное периодическое колебание представляет собой набор гармонических колебаний, что поясняется следующим рисунком.

Здесь сложное колебание г) разложено на гармонические колебания а), б) и в), каждое из которых характеризуется своей частотой.

Частота колебания а), называемого основным тоном, равна величине, обратной периоду 1/Т сложного колебания г).

Все другие гармонические колебания, имеющие свои более высокие частоты, называются обертонами.

Из рисунка видно, что частота обертона б) в три раза выше частоты основного тона. а частота обертона в) в пять раз выше частоты основного тона.

Чем сложнее звуковое колебание, тем из большего количества обертонов оно состоит. Одновременное звучание основного тона и обертонов определяет тембр (окраску) звука.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.

Предыдущая запись: Почему камертон излучает слабый звук и как усилить этот звук?

Следующая запись: Магнетизм вещества. Как наука объясняет это явление? Парамагнетики. Диамагнетики.

Ссылки на занятия до электростатики даны в Занятии 1 .

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .

Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.

Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .

Колебания струны, формула частоты колебаний

[ f = frac{1}{2l} sqrt{frac{F}{ρS}} ]

Формула определяет частоту основных колебаний струны (основного тона). Кроме того, возможны колебания с более высокими частотами (обертоны). Обертоны влияют на тембр звука, но не меняют частоты воспринимаемого тона.

Вычислить, найти частоту колебания струны по формуле (1)

В сфере распознавания эмоций голос – второй по важности после лица источник эмоциональных данных. Голос можно охарактеризовать по нескольким параметрам. Высота голоса – одна из основных таких характеристик, однако в сфере акустических технологий корректнее называть этот параметр частотой основного тона.

Частота основного тона имеет непосредственное отношение к тому, что мы называем интонацией. А интонация, например, связана с эмоционально-экспрессивными характеристиками голоса.

Тем не менее, определение частоты основного тона является не совсем тривиальной задачей с интересными нюансами. В этой статье мы обсудим особенности алгоритмов для ее определения и сравним существующие решения на примерах конкретных аудиозаписей.

Введение

Для начала вспомним, чем, по сути, является частота основного тона и в каких задачах она может понадобиться. Частота основного тона, которую еще обозначают как ЧОТ, Fundamental Frequency или F0 – это частота колебания голосовых связок при произнесении тоновых звуков (voiced). При произнесении нетоновых звуков (unvoiced), например говорении шепотом или произнесении шипящих и свистящих звуков, связки не колеблются, а значит эта характеристика для них не релевантна.

* Обратите внимание, что деление на тоновые и не тоновые звуки не эквивалентно делению на гласные и согласные.

Вариабельность частоты основного тона довольно велика, причем она может сильно отличаться не только между людьми (для более низких в среднем мужских голосов частота составляет 70-200 Гц, а для женских может достигать 400 Гц), но и для одного человека, особенно в эмоциональной речи.

Определение частоты основного тона применяется для решения широкого спектра задач:

• Распознавание эмоций, как мы уже сказали выше;
• Определение пола;
• При решении задачи сегментации аудио с несколькими голосами или разделения речи на фразы;
• В медицине для определения патологических характеристик голоса (например, с помощью акустических параметров Jitter and Shimmer). Например, определение признаков заболевания Паркинсона [1]. Jitter and Shimmer также могут быть использованы для распознавания эмоций [2].

Однако при определении F0 существует ряд сложностей. К примеру, часто можно перепутать F0 с гармониками, что может привести к так называемым эффектам pitch doubling/pitch halving [3]. А в аудиозаписи плохого качества F0 вычислить бывает довольно сложно, так как нужный пик на низких частотах практически исчезает.

Кстати, помните историю про Laurel и Yanny? Различия в том, какие слова слышат люди при прослушивании одной и той же аудиозаписи, возникли как раз из-за разницы в восприятии F0, на которую влияют много факторов: возраст слушающего, степень усталости, устройство воспроизведения. Так, при прослушивании записи в колонках с качественным воспроизведением низких частот, вы будете слышать Laurel, а в аудиосистемах, где низкие частоты воспроизводятся плохо, Yanny. Эффект перехода можно заметить и на одном устройстве, например здесь. А в этой статье в качестве слушателя выступает нейросеть. В другой статье можно почитать, как объясняется феномен Yanny/Laurel с позиций речеобразования.

Поскольку подробный разбор всех методов определения F0 был бы чересчур объемным, статья носит обзорный характер и может помочь сориентироваться в теме.

Методы определения F0

Методы определения F0 можно разделить на три категории: основанные на временной динамике сигнала, или time-domain; основанные на частотной структуре, или frequency-domain, а также комбинированные методы. Предлагаем ознакомиться с обзорной статьей по теме, где подробно разбираются обозначенные методы выделения F0.

Отметим, что любой из обсуждаемых алгоритмов состоит из 3 основных шагов:

Препроцессинг (фильтрация сигнала, разделение его на фреймы)
Поиск возможных значений F0 (кандидатов)
Трекинг — выбор наиболее вероятной траектории F0 (поскольку для каждого момента времени мы имеем несколько конкурирующих кандидатов, нам необходимо найти среди них наиболее вероятный трек)

Time-domain

Очертим несколько общих моментов. Перед применением методов time-domain сигнал предварительно фильтруют, оставляя только низкие частоты. Задаются пороги – минимальная и максимальная частоты, например от 75 до 500 Гц. Определение F0 производится только для участков с гармонической речью, поскольку для пауз или шумовых звуков это не только бессмысленно, но и может внести ошибки в соседние фреймы при применении интерполяции и/или сглаживании. Длину фрейма выбирают так, чтобы в ней содержалось как минимум три периода.

Основной метод, на базе которого впоследствии появилось целое семейство алгоритмов – автокорреляционный. Подход достаточно прост — необходимо рассчитать автокорреляционную функцию и взять ее первый максимум. Он и будет отображать самую выраженную частотную компоненту в сигнале. В чем может быть сложность в случае использования автокорреляции и почему далеко не всегда первый максимум будет соответствовать нужной частоте? Даже в близких к идеальным условиям на записях высокого качества метод может ошибаться из-за сложной структуры сигнала. В условиях близких к реальным, где помимо прочего мы можем столкнуться с исчезновением нужного пика на шумных записях или записях изначально низкого качества, число ошибок резко возрастает.

Несмотря на ошибки, автокорреляционный метод довольно удобен и привлекателен своей базовой простотой и логичностью, поэтому именно он взят за основу во многих алгоритмах, в том числе в YIN (Инь). Даже само название алгоритма отсылает нас к балансу между удобством и неточностью метода автокорреляции: “The name YIN from ‘‘yin’’ and ‘‘yang’’ of oriental philosophy alludes to the interplay between autocorrelation and cancellation that it involves.” [4]

Создатели YIN попытались исправить слабые места автокорреляционного подхода. Первое изменение – использование функции Cumulative Mean Normalized Difference, которая должна снизить чувствительность к амплитудным модуляциям, сделать пики более явными:

begin{equation}
d’_t(tau)=
begin{cases}
1, & tau=0 \
d_t(tau) bigg/ bigg[ frac{1}{tau} sumlimits_{j=1}^{tau} d_t(j) bigg], & text{otherwise}
end{cases}
end{equation}
Также YIN пытается избежать ошибок, возникающих в случаях, когда длина оконной функции не делится нацело на период колебания. Для этого используется параболическая интерполяция минимума. На последнем шаге обработки аудиосигнала выполняется функция Best Local Estimate для предотвращения резких скачков значений (хорошо это или плохо – вопрос спорный).

Frequency-domain

Если говорить о частотной области, то на первый план выходит гармоническая структура сигнала, то есть наличие спектральных пиков на частотах, кратных F0. “Свернуть” этот периодический паттерн в явный пик можно при помощи кепстрального анализа. Кепстр — преобразование Фурье от логарифма спектра мощности; кепстральный пик соответствует наиболее периодической компоненте спектра (про него можно почитать здесь и здесь).

Гибридные методы определения F0

Следующий алгоритм, на котором стоит остановиться поподробнее, имеет говорящее название YAAPT — Yet Another Algorithm of Pitch Tracking — и фактически является гибридным, потому что использует как частотную, так и временную информацию. Полное описание есть в статье, здесь мы опишем только основные этапы.

Рисунок 1. Схема алгоритма YAAPTalgo (ссылка).

YAAPT состоит из нескольких основных этапов, первым из которых является препроцессинг. На этом этапе значения изначального сигнала возводят в квадрат, получают вторую версию сигнала. Этот шаг преследует ту же цель, что и Cumulative Mean Normalized Difference Function в YIN – усиление и восстановление “затертых” пиков автокорреляции. Обе версии сигнала фильтруют — обычно берут диапазон 50-1500 Гц, иногда 50-900 Гц.

Затем по спектру преобразованного сигнала рассчитывается базовая траектория F0. Кандидаты на F0 определяются с помощью функции Spectral Harmonics Correlation (SHC).

begin{equation}
SHC(t,f) = sumlimits_{f’=-WL/2}^{WL/2} prodlimits_{r=1}^{NH+1}S(t,rf+f’)
end{equation}
где S(t,f) — магнитудный спектр для фрейма t и частоты f, WL — длина окна в Гц, NH — число гармоник (авторы рекомендуют использовать первые три гармоники). Также по спектральной мощности происходит определение фреймов voiced-unvoiced, после чего ищется наиболее оптимальная траектория, при этом учитывается возможность pitch doubling/pitch halving [3, Section II, C].

Далее, как для изначального сигнала, так и для преобразованного производится определение кандидатов на F0, и вместо автокорреляционной функции здесь используется Normalized Cross Correlation (NCCF).

begin{equation}
NCCF(m) = frac{sumlimits_{n=0}^{N-m-1} x(n)*x(n+m)}{sqrt{sumlimits_{n=0}^{N-m-1} x^2(n) * sumlimits_{n=0}^{N-m-1} x^2(n+m)}}text{,} hspace{0.3cm} 0 < m < M_{0}
end{equation}
Следующий этап — оценка всех возможных кандидатов и вычисление их значимости, или веса (merit). Вес кандидатов, полученных по аудио сигналу, зависит не только от амплитуды пика NCCF, но и от их близости к траектории F0, определенной по спектру. То есть частотный домен считается хоть и грубым в плане точности, но зато устойчивым [3, Section II, D].

Затем для всех пар оставшихся кандидатов рассчитывается матрица Transition Cost — цены перехода, по которой в итоге и находят оптимальную траекторию [3, Section II, E].

Примеры

Теперь применим все вышеописанные алгоритмы к конкретным аудиозаписям. В качестве отправной точки будем использовать Praat — инструмент, который является основным для многих исследователей речи. А затем на Python посмотрим реализацию YIN и YAAPT и сравним полученные результаты.

В качестве аудио-материала можно использовать любые доступные аудио. Мы взяли несколько отрывков из нашей базы RAMAS — мультимодального датасета, созданного при участии актеров ВГИК. Можно также воспользоваться материалом из других открытых баз, например LibriSpeech или RAVDESS.

Для наглядного примера мы взяли отрывки из нескольких записей с мужским и женским голосами, как нейтральными, так и эмоционально-окрашенными, и для наглядности соединили их в одну запись. Посмотрим на наш сигнал, его спектрограмму, интенсивность (оранжевый цвет), и F0 (синий цвет). В Praat это можно сделать при помощи Ctrl+O (Open — Read from file) и затем кнопки View & Edit.

Рисунок 2. Спектрограмма, интенсивность (оранжевый цвет), F0 (синий цвет) в Praat.

На аудио довольно четко видно, что при эмоциональной речи высота голоса повышается как у мужчин, так и у женщин. При этом F0 для эмоциональной мужской речи вполне может сравниться с F0 женского голоса.

Трекинг

Выберем в меню Praat вкладку Analyze periodicity – to Pitch (ac), то есть определение F0 при помощи автокорреляции. Появится окно для задания параметров, в котором есть возможность задать 3 параметра для определения кандидатов на F0 и еще 6 параметров для алгоритма поиска пути (path-finder), который выстраивает наиболее вероятную траекторию F0 среди всех кандидатов.

Подробное описание алгоритма можно найти в статье 1993 года.

Как выглядит результат работы трекера (path-finder) можно посмотреть, нажав ОК и затем просмотрев (View & Edit) получившийся файл Pitch. Видно, что помимо выбранной траектории были еще довольно значимые кандидаты с частотой ниже.

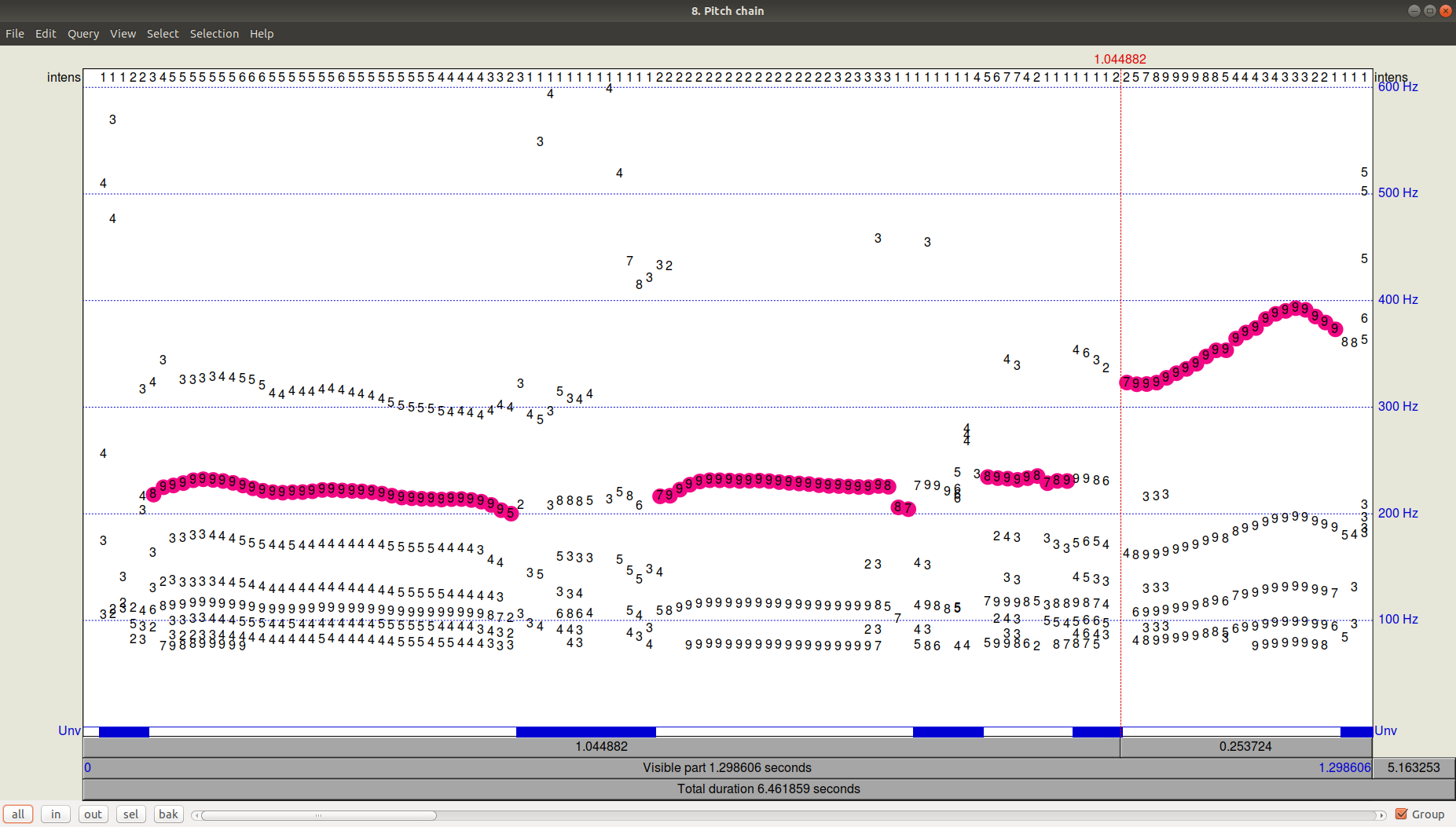
Рисунок 3. PitchPath для первых 1,3 секунд аудиозаписи.

А что же в Python?

Возьмем две библиотеки, предлагающих питч-трекинг – aubio, в которой алгоритмом по умолчанию является YIN, и библиотеку AMFM_decompsition, в которой есть реализация алгоритма YAAPT. В отдельный файл (файл PraatPitch.txt) вставим значения F0 из Praat (это можно сделать вручную: выбрать звуковой файл, нажать View & Edit, выделить весь файл и выбрать в верхнем меню Pitch-Pitch listing).

Теперь сравним результаты по всем трем алгоритмам (YIN, YAAPT, Praat).

import amfm_decompy.basic_tools as basic
import amfm_decompy.pYAAPT as pYAAPT
import matplotlib.pyplot as plt
import numpy as np
import sys
from aubio import source, pitch

# load audio
signal = basic.SignalObj('/home/eva/Documents/papers/habr/media/audio.wav')
filename = '/home/eva/Documents/papers/habr/media/audio.wav'

# YAAPT pitches
pitchY = pYAAPT.yaapt(signal, frame_length=40, tda_frame_length=40, f0_min=75, f0_max=600)

# YIN pitches
downsample = 1
samplerate = 0
win_s = 1764 // downsample # fft size
hop_s = 441 // downsample # hop size
s = source(filename, samplerate, hop_s)
samplerate = s.samplerate
tolerance = 0.8
pitch_o = pitch("yin", win_s, hop_s, samplerate)
pitch_o.set_unit("midi")
pitch_o.set_tolerance(tolerance)

pitchesYIN = []
confidences = []

total_frames = 0
while True:
    samples, read = s()
    pitch = pitch_o(samples)[0]
    pitch = int(round(pitch))
    confidence = pitch_o.get_confidence()
    pitchesYIN += [pitch]
    confidences += [confidence]
    total_frames += read
    if read < hop_s:
        break
        
# load PRAAT pitches
praat = np.genfromtxt('/home/eva/Documents/papers/habr/PraatPitch.txt', filling_values=0)
praat = praat[:,1]

# plot       
fig, (ax1,ax2,ax3) = plt.subplots(3, 1, sharex=True, sharey=True, figsize=(12, 8))
ax1.plot(np.asarray(pitchesYIN), label='YIN', color='green')
ax1.legend(loc="upper right")
ax2.plot(pitchY.samp_values, label='YAAPT', color='blue')
ax2.legend(loc="upper right")
ax3.plot(praat, label='Praat', color='red')
ax3.legend(loc="upper right")
plt.show()

Рисунок 4. Сравнение работы алгоритмов YIN, YAAPT и Praat.

Мы видим, что при заданных по умолчанию параметрах YIN довольно сильно выбивается, получая очень плоскую траекторию с заниженными относительно Praat значениями и полностью теряя переходы между мужским и женским голосом, а также между эмоциональной и не эмоциональной речью.

YAAPT зарезал совсем высокий тон при эмоциональной женской речи, но в целом справился явно лучше. За счет каких своих особенностей YAAPT работает лучше — сразу ответить точно, конечно, нельзя, но можно предположить, что роль играет получение кандидатов из трех источников и более скрупулезный расчет их веса, чем в YIN.

Заключение

Поскольку вопрос определения частоты основного тона (F0) в том или ином виде встает почти перед каждым, кто работает со звуком, путей для его решения достаточно много. Вопрос необходимой точности и особенности аудиоматериала в каждом конкретном случае определяют, насколько внимательно необходимо подбирать параметры, или в ином случае можно ограничиться базовым решения наподобие YAAPT. Принимая Praat за эталон алгоритма для обработки речи (все же им пользуется огромное количество исследователей), можно сделать вывод о том, что YAAPT в первом приближении надежнее и точнее, чем YIN, хотя и для него наш пример оказался сложноват.

Автор: Ева Казимирова, научный сотрудник Neurodata Lab, специалист по обработке речи.

Оффтоп: Понравилась статья? На самом деле у нас куча подобных интересных задач по ML, математике и программированию, и нам нужны мозги. Тебе такое интересно? Приходи к нам! E-mail: hr@neurodatalab.com

А.Н. Голубинский,

кандидат технических наук

РАСЧЁТ ЧАСТОТЫ ОСНОВНОГО ТОНА РЕЧЕВОГО СИГНАЛА НА ОСНОВЕ ПОЛИГАРМОНИЧЕСКОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

CALCULATION OF THE PITCH FREQUENCY OF A SPEECH SIGNAL ON THE BASIS OF POLYHARMONICAL MATHEMATICAL MODEL

Предложена методика расчёта оценки частоты основного тона речевого сиг -нала на основе минимума невязки коэффициентов корреляции. Проведено сравнение данного метода оценки частоты основного тона с амплитудным, корреляционным, спектральным и вейвлет методами.

The method of calculation of the pitch frequency estimation of a speech signal on the basis of minimum misalignment correlation coefficients is proposed. The comparison of the given method of the pitch frequency estimation with amplitude, correlation, spectral and wavelet methods is carried out.

Одним из актуальных практических направлений обработки сигналов в охранных системах является обработка звуковых и речевых сигналов. При этом важнейшим параметром речи, применительно к задачам кодирования, сжатия, идентификации и верификации по речевому сигналу, является частота основного тона речевого сигнала для вокализованных участков речи [1].

Однако на пути вычисления оценки частоты основного тона встаёт ряд трудностей, основными из которых являются:

– сложность алгоритмов получения оценки;

– низкая точность оценки;

– наличие ошибок, связанных с грубыми промахами (например, принятие за оценку частоты основного тона частоты первого или второго обертона);

– неустойчивость алгоритма вычисления оценки (например, к шумам или эмоциональной окраске речи).

Таким образом, представляет научный интерес разработка методов оценки частоты основного тона, которые лишены указанных недостатков.

Цель работы — разработка метода расчёта оценки частоты основного тона речевого сигнала на основе минимума невязки между коэффициентами корреляции, рассчитанными по экспериментальным данным и по специальной тестовой математической модели речевого сигнала.

Принято считать [2—5], что на участках вокализованного звука речевой тракт человека возбуждается периодическим колебанием связок. Период этого колебания называют периодом основного тона. Эта величина является индивидуальной характеристикой диктора. Она может меняться в зависимости от эмоциональной окраски речи, но в достаточно узких пределах. В процессе исследования речи установлено, что частота основного тона человека лежит в пределах 50—350 Гц.

Существуют следующие основные методы оценки частоты основного тона речевого сигнала :

1) методы, основанные на амплитудной селекции (амплитудные методы);

2) корреляционные методы;

3) методы, основанные на частотной селекции (спектральные методы);

4) методы на основе вейвлет-преобразования;

5) методы на основе кепстрального анализа;

6) методы на основе линейного предсказания.

Рассмотрим подробнее каждый из указанных методов.

В амплитудном методе на стационарном участке вокализованного звука при малом уровне шумов форма речевого колебания почти точно повторяется на каждом очередном периоде основного тона. Расстояние между глобальными максимумами (максимумами максиморумами) речевого сигнала можно приблизительно считать равным периоду основного тона. Основная трудность алгоритмов амплитудной селекции состоит в необходимости подавления локальных ложных максимумов. Этого можно добиться за счёт повышения порога срабатывания в схеме поиска максимумов. Однако при этом увеличивается вероятность пропуска истинного максимума. Очевидно, что как пропуск, так и потеря максимума может привести к существенным искажениям синтезированного звука. Повысить надёжность определения периода основного тона можно, например, добавив второй канал амплитудной селекции, выделяющий положение минимумов речевого сигнала. Главным достоинством устройств временной селекции является чрезвычайная простота реализации. Основные недостатки: низкая точность и неустойчивость определения основного тона (даже при относительно небольшом уровне шумов).

Корреляционные методы определения периода основного тона речевого сигнала базируются на оценке среднего значения периода пульсаций квазипериодической корреляционной функции [3] (или, в частном случае, вычислении первого глобального максимума корреляционной функции [6]). Частота основного тона /1 рассчитывается по соотношению:

/1=/-, (1)

Ир-1

где /^ — частота дискретизации; Ир _ — среднее число отсчётов корреляционной функции, через которое пульсации повторяются [7]; р — число глобальных максимумов корреляционной функции, взятых для усреднённой оценки Ир _1 .

В частном случае, основанном на поиске первого глобального максимума, применяется следующий подход. Пусть речевой сигнал представлен в виде последовательности отсчётов. Для вокализованных звуков можно считать, что временной вид речевого колебания почти точно повторяется на каждом очередном периоде основного тона. В качестве оценки периода основного тона Т = 1/ /1 , выраженной в числе отсчётов, выбирают значение, минимизирующее целевую функцию, которая определяется как сумма квадратов разностей между отсчётами сигнала и отсчётами сигнала, смещёнными на некоторое число отсчётов [6]. Если предположить, что энергия речевого сигнала не меняется на участке квазистационарности, то оценка периода основного тона должна максимизировать корреляционную функцию. Данный подход обеспечивает существенно более высокую достоверность определения периода основного тона по сравнению с методами временной селекции. При этом следует отметить значительную вычислительную сложность данного алгоритма. Существуют его модификации, основанные на вычислении взаимной корреляционной функции с подобранной функцией, которая клип-пирует речевой сигнал на три уровня {-1, 0, 1} (трёхуровневый ограничитель). Таким образом, можно упростить алгоритм, сделав его пригодным для аппаратной реализации, тогда вычислитель взаимной корреляционной функции можно построить без ум-

ножителя [8]. Рассмотренные корреляционные методы оценивания периода основного тона имеют общий недостаток: неустойчивую работу в случае, когда речевой сигнал модулирован по амплитуде. Энергия же реальной, т.е. эмоционально окрашенной речи изменяется даже на квазистационарных участках, соответствующих одной фонеме. В этом случае применяется модифицированная целевая функция, в которой смещённые отсчёты сигнала умножаются на некоторый параметр, имеющий смысл коэффициента усиления [8]. Метод позволяет получить достаточно точную оценку основного тона, которая плавно меняется во времени в соответствии с изменениями голоса. Поэтому данный алгоритм используется в стандарте 0.723, регламентирующем способ сжатия речевого сигнала для видеоконференций.

Спектральный метод основан на том, что при вокализованном возбуждении речевого тракта в спектре сигнала присутствуют пики на частотах, кратных частоте основного тона. Если построить дискретное преобразование Фурье с достаточно малым шагом дискретизации по частоте, то можно попытаться в качестве оценки частоты основного тона использовать частоту, соответствующую максимальному значению энергии спектра. Поиск максимума следует производить в интервале 50—350 Гц. Однако часто возникает ситуация, когда в указанной полосе лежит и вторая гармоника основного тона, иногда даже с большей энергией. В этом случае она будет ошибочно принята за оценку основного тона. Чтобы избежать этого, обычно ищут максимум не спектра, а некоторой нелинейной функции от спектра [8]. Эта функция, как правило, представляет собой сумму сжатых по частоте в несколько раз логарифмов спектра мощности. Суть идеи состоит в том [8], что для истинной частоты основного тона вторая гармоника второго слагаемого сложится с первой гармоникой первого слагаемого и усилит её. Аналогично для третьего слагаемого и т. д. В результате для вокализованного звука будет иметь место ярко выраженный пик функции (от спектра) на частоте основного тона, а для невокализованного звука суммирование будет иметь хаотический характер.

Заметим, что в общем случае оценка значений спектра является несостоятельной и может иметь большие погрешности. Для уменьшения ошибки оценки спектральных составляющих, например нормированной спектральной плотности мощности (также часто используют дискретное преобразование Фурье, или быстрое преобразование Фурье), применяют методику спектральных окон. Выбор спектрального окна (весовой функции) при анализе определяется в результате компромисса между разрешающими способностями по частоте и во времени [4, 9]. Следует отметить, что для спектральных методов применение нелинейного преобразования спектра и окон может вносить большие смещения, что существенно ухудшает точность оценки.

Относительно новый развивающийся метод (см., например, [10]) оценки частоты основного тона речевого сигнала на основе вейвлет-преобразования базируется на применении непрерывного или дискретного вейвлет-преобразования. Следует отметить положительную сторону данного метода: для генерированного эталонного четырёхгармонического сигнала относительная погрешность оценки частоты основного тона и формантных частот методом вейвлет-преобразования не превышала 0,38% [10]. Недостатки данного метода: необходимость корректировки окна преобразования под каждую оцениваемую частоту; сложность алгоритма реализации метода; большие вычислительные затраты.

Метод оценивания основного тона на основе кепстрального анализа состоит в вычислении и анализе кепстра — обратного преобразования Фурье логарифма спектра мощности сигнала [8]. Однако данный метод имеет ряд существенных недостатков, таких как: необходимость применения дополнительной методики для вычисления порога для оценки периода основного тона в области возможных значений; работа в нереальном масштабе времени; необходимость применения временных окон и операций сгла-

живания; низкая точность оценки при сильной узкополосности гармоники основного тона [8].

Среди методов оценки на основе линейного предсказания обычно используют метод обратной фильтрации (обратный линейный фильтр). При приближении частоты повторения в обратном фильтре к частоте основного тона происходит всё более и более сильное выравнивание спектра. Одна из трудностей — это постоянный расчёт спектра речевого сигнала при подстройке частоты повторения в обратном фильтре. Метод даёт удовлетворительные оценки, пока спектр выравнивается достаточно хорошо, однако здесь стоит новая задача определения степени равномерности спектра после обратной фильтрации. Также следует отметить, что при частотах основного тона выше 200 Гц данный метод оценки приводит к плохим результатам [6].

Суть предлагаемого метода расчёта оценки частоты основного тона речевого сигнала на основе минимума невязки коэффициентов корреляции при использовании полигармони-ческой математической модели заключается в следующем. Частоту основного тона будем оценивать на основе определения минимума невязки коэффициентов корреляции. Невязка определяется между значениями коэффициентов корреляции, полученных на основе экспериментальных данных, и коэффициентами тестовой (специальной для оценки основного тона) математической модели речи, содержащей вокализованные участки. Оценка /0 частоты основного тона /0 определяется как значение аргумента, при котором наблюдается наименьшее значение невязки еКТе&1 (/0) в диапазоне частот [3] от 50 до 350 Гц (с шагом, например, А/0 =0,1 Гц или менее, при необходимости большей точности оценки):

где ЯаТе81 (/’А, /0) — коэффициент корреляции тестовой математической модели речевого сигнала, применяемый для оценки частоты основного тона; Я/ — коэффициент корреляции центрированного речевого сигнала;

Звуковые платы ЭВМ, как правило, добавляют различные постоянные составляющие в речевой сигнал. В связи с этим для удобства последующей обработки речевого сигнала над отсчётами полученной реализации случайного процесса проводилась операция центрирования реализации:

/0 = arg inf [eRTest (/0)], здесь тестовая невязка (ошибка):

(2)

eRTest(/0) = 2(RaTest(JA,/0) -Rj j2 ,

J=1

(3)

(4)

здесь функция корреляции:

1 N _ / _

к/ = N 2 ( у > _ у )( у+/

i = 1

у), / = 0, J; J — число отсчётов коэффициентов корреля-

i =1

— ма-

(5)

тематическое ожидание начальных отсчётов речевого сигнала. Для центрированной реализации (5): у = 0 .

Запишем упрощённый вид коэффициента корреляции тестовой (трёхгармонической) математической модели речевого сигнала:

1 3

RaTest(у’Л, /о) = – ^ cos(2p/ fo j А) . (6)

3 /=0

Используя данную оригинальную методику, можно довольно просто (без применения сложных алгоритмов вычисления) получить высокоточную оценку частоты основного тона fo речевого сигнала, содержащего вокализованные участки речи. Следует отметить, что увеличение количества гармоник более трёх не приводит к существенному увеличению точности оценки.

Более общий вид коэффициента корреляции тестовой математической модели речевого сигнала рассчитывается на основе стохастического подхода при использовании квазидетерминированной математической модели речевого сигнала [11]:

L

u(t) = Mcos[2pFot + Фо]^U/ cos[2p/fot + j/], te[0;tM ], (7)

/ =0

где Ф 0 и j/ — случайные величины, не коррелированные между собой и равномерно

распределённые в интервале [0;2p]; F0 — частота модулирующего колебания; U/ — амплитуда /-й гармоники несущего колебания; f0 — частота основного тона; M — глубина модуляции; ти — длительность импульса. Можно показать, что данный случайный процесс является стационарным в широком смысле и эргодическим.

Таким образом, общий вид коэффициента корреляции тестовой математической модели речевого сигнала:

M2 L

Ku(t) =—cos(2pF0t)^U/2cos(2p/f0T) . (8)

2 /=0

Для дискретных отсчётов функции корреляции t = j Л, j = 1, J:

M 2 L

KaTest( jA f0 ) = cos(2 pF0 j A)^ U/ cos(2 p/ f j Л); (9)

2 /=0

ЯаТеЯСта,/о) = КТ15А1‘В= сов(2Р0;Д)^Ц?со8(2р/./оТ А) / Ги1 ■ (10)

КаТезКО,,/о) ¡=0 / ¡=0

При равенстве всех амплитуд р единице для количества гармоник в полигармониче-ской модели, равного трём (¿=3, трёхгармоническая модель), если положить Fo = 0 (случай отсутствия модуляции несущих гармоник — нет информационного сигнала, который не описывает индивидуальные особенности голоса [11]), тестовая математическая модель упрощается, и коэффициент корреляции принимает вид (6).

Для расчёта оценки частоты основного тона речевого сигнала будем использовать персональную ЭВМ, ввод речевого сигнала в которую выполняется с помощью звуковой платы, со стандартной частотой дискретизации /^ =6000 Гц. Данная частота была выбрана вследствие того, что первые 3-4 форманты находятся в области до 3000—3600 Гц [3, 4]. При увеличении частоты дискретизации возможно повышение точности оценки частоты основного тона при одновременном увеличении ресурсов обработки массивов данных.

Определим число отсчётов КК J, достаточное для анализа характеристик математической модели. Проведённый анализ речевых сигналов различных дикторов показал, что все значения КК заходят в доверительные границы, полученные по методу Бартлетта [12] ± 3s до 200-го отсчёта (для fd =6000 Гц), таким образом, выберем J =200.

В результате исследования зависимости eRTest (f0) было выяснено, что аргумент f0 (оценка частоты основного тона) глобального минимума inf [eRTest (f0)], если использовать в коэффициенте корреляции (10) только три слагаемых суммы — тестовая трёхгармоническая модель (6), имеет достаточно хорошую точность оценки. Дальнейшее увеличение количества гармоник приводит, как правило, к несущественному возрастанию точности оценки (относительная погрешность оценки основного тона для тестовых сигналов увеличивалась не более чем на 0,1%). Также было установлено, что если амплитудные коэффициенты положить равными единице, то оценка частоты основного тона практически не смещается (относительное смещение менее 0,05%).

Рис. 1 поясняет сущность предлагаемого метода на примере упрощённой тестовой математической модели, при использовании реального речевого сигнала (слово “он”). На рис. 1 сплошной линией показан график зависимости коэффициентов корреляции речевого сигнала (оценка частоты основного тона по разработанному методу составила f = 155,2 Гц) от номера отсчёта; штрихпунктирной, штриховыми и пунктирными линиями изображены зависимости коэффициентов корреляции тестовой трёхгармонической математической модели, при этом частоты основного тона тестовой модели были заданы соответственно: = 155,2 Гц, f0 = 155,2±5 Гц и f0 = 155,2± 10 Гц.

Из графиков коэффициентов корреляции, приведённых на рис. 1, видно, что даже при незначительной неточности оценки частоты основного тона происходит значительное увеличение тестовой ошибки из-за существенного рассогласования между коэффициентом корреляции, рассчитанным по экспериментальным данным (речевого сигнала), и коэффициентом корреляции тестовой математической модели.

Поэтому даже упрощённая тестовая математическая модель даёт результаты оценки частоты основного тона с высокой точностью. Следует отметить, что возможно применение и более общей тестовой математической модели (10), однако с одновременным увеличением точности оценки происходит усложнение алгоритма обработки в связи с необходимостью дополнительно адаптивно оценивать амплитуды гармоник.

Рис. 1. График коэффициентов корреляции речевого сигнала и тестовой трёхгармонической математической модели при различных значениях частоты основного тона для тестового сигнала

Для анализа качества работы предложенного метода оценки основного тона генерировались различные эталонные полигармонические сигналы. В данной работе приведены результаты анализа при использовании эталонного четырёхгармонического сигнала (с постоянной составляющей) следующего вида:

где иЭТ = 142; иЭТ = 14; и^ =14; иЭТ = 14; и^Т = 14. Параметры данного сигнала были выбраны такими же, как и в работе [10], для удобства сравнения точностных характеристик предлагаемого метода оценки частоты основного тона с методом, основанным на вейвлет-преобразовании.

В результате оценки частоты основного тона /0 генерированного эталонного че-

в диапазоне частот от 50 до 345 Гц), при использовании тестовой трёхгармонической математической модели было установлено, что модуль относительной погрешности оценки

не превышает 0,3%. Например, для значения частоты основного тона генерированного эталонного сигнала /0 = 155 Гц, оценка частоты основного тона имела значение

/о = 155,02 Гц, при этом модуль относительной погрешности оценки составил 0,013 %.

В качестве практической проверки разработанного метода оценки частоты основного тона речевого сигнала проводился расчёт оценки частоты основного тона для 5 произнесённых гласных звуков для 10 различных дикторов. Также проводилось сравнение точности оценки частоты основного тона с ранее известными другими четырьмя методами. В результате анализа оценок частоты основного тона было установлено, что точность разработанного метода оценки частоты основного тона речевого сигнала на основе минимума невязки коэффициентов корреляции при использовании полигармонической математической модели в подавляющем большинстве случаев является наибольшей по сравнению с ранее известными другими методами. При этом точность оценки, полученная на основе предлагаемого метода:

– оказывается одного порядка с точностью оценки методом, основанным на вейвлет-преобразовании;

– примерно превышает на порядок точность оценки корреляционным и спектральным методами;

– в основном превышает более чем на порядок точность оценки амплитудным методом.

Данное сравнение проводилось с использованием генерированных эталонных

ь

(11)

I =0

ЭТ

тырёхгармонического сигнала для 60 различных частот основного тона /0 (каждые 5 Гц

5 л = /0 м 10000,

/0

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

(12)

полигармонических сигналов.

В качестве примера зависимости тестовой ошибки от частоты тестового сигнала, приведём рис. 2 для одного из дикторов, произносящего вокализованный участок речи

— слово «он». Для данного случая глобальный минимум (оценка частоты основного тона речевого сигнала) наблюдался на частоте / = 155,2 Гц.

Рис. 2. Тестовая ошибка для реального речевого сигнала при использовании тестовой трёхгармонической математической модели

На основании проведённых расчётов по разработанному методу оценки частоты основного тона с использованием тестового сигнала и при сравнении с другими методами оценки можно заключить, что предлагаемый метод обеспечивает наибольшую точность оценки частоты основного тона, относительная погрешность при этом не превышает 0,3% при шаге А/0 =0,1 Гц.

Таким образом, разработан метод расчёта частоты основного тона речевого сигнала на основе минимума невязки между коэффициентами корреляции при использовании полигармонической математической модели. Предлагаемый метод оценки частоты основного тона является достаточно простым для реализации в виде алгоритмов расчёта при одновременном обеспечении высокой точности оценки.

ЛИТЕРАТУРА

1. Сорокин В.Н. Фундаментальные исследования речи и прикладные задачи речевых технологий / В.Н. Сорокин // Речевые технологии. — 2008. — № 1. — С. 18—48.

2. Прохоров Ю.Н. Статистические модели и рекуррентное предсказание речевых сигналов / Ю.Н. Прохоров. — М.: Радио и связь, 1984. — 240 с.

3. Назаров М.В. Методы цифровой обработки и передачи речевых сигналов / М.В. Назаров, Ю. Н. Прохоров. – М.: Радио и связь, 1985. — 176 с.

4. Фланаган Дж. Анализ, синтез и восприятие речи / Дж. Фланаган. — М.: Связь, 1968. — 392 с.

5. Фант Г. Анализ и синтез речи / Г. Фант.— Новосибирск: Наука, 1970. — 306 с.

6. Маркел Дж. Линейное предсказание речи / Дж. Маркел, А.Х. Грей. — М.: Связь, 1980. — 308 с.

7. Ролдугин С. В. Модели речевых сигналов для идентификации личности по

голосу / С. В. Ролдугин, А.Н. Голубинский, Т.А. Вольская // Радиотехника. — 2002.

— №11. — С. 79—81.

8. Рабинер Л.Р. Цифровая обработка речевых сигналов / Л.Р. Рабинер, Р.В. Шафер. — М.: Радио и связь, 1981. — 496 с.

9. Голубинский А.Н. Модель речевого сигнала в виде импульса АМ-колебания с несколькими несущими для верификации личности по голосу / А.Н. Голубинский // Системы управления и информационные технологии. — 2007. — № 4. — С. 86—91.

10. Рассказова С. И. Метод формантного анализа на основе вейвлет-преобразования в системах распознавания речи / С.И. Рассказова, А.И. Власов // Наукоемкие технологии и интеллектуальные системы: сборник трудов IX Научнотехнической конференции. — М.: МГТУ им. Н.Э. Баумана, 2007. — С. 38—43.

11. Голубинский А.Н. Разработка математической модели речевого сигнала в виде импульса АМ-колебания с несколькими несущими частотами, применительно к задаче верификации личности по голосу / А.Н. Голубинский; Воронежский институт МВД России. — Воронеж, 2008. — 29 с. — Деп. в ВИНИТИ 09.07.08, №591-В2008.

12. Бокс Дж. Анализ временных рядов. Прогноз и управление / Дж. Бокс, Г. Дженкинс. — М.: Мир, 1974.— Вып.2. — 408 с.