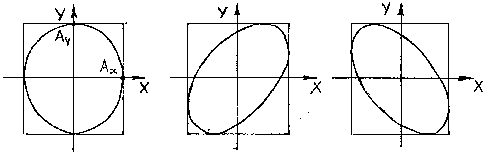Частота складываемых колебаний как найти

2.1. Сложение гармонических колебаний одного направления

2.2. Сложение взаимно перпендикулярных колебаний

Одно и то же тело может одновременно участвовать в двух и более движениях. Простым примером является движение шарика, брошенного под углом к горизонту. Можно считать, что шарик участвует в двух независимых взаимно перпендикулярных движениях: равномерном по горизонтали и равнопеременном по вертикали. Одно и то же тело (материальная точка) может участвовать в двух (и более) движениях колебательного типа.

Под сложением колебаний понимают определение закона результирующего колебания, если колебательная система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая – сложение колебаний одного направления и сложение взаимно перпендикулярных колебаний.

2.1. Сложение гармонических колебаний одного направления

1. Сложение двух колебаний одного направления (сонаправленных колебаний)

можно провести с помощью метода векторных диаграмм (Рисунок 9) вместо сложения двух уравнений.

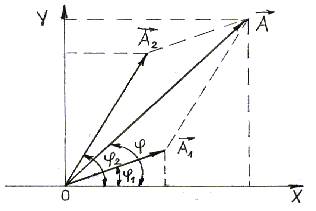
На Рисунке 2.1 показаны векторы амплитуд А₁(t) и А₂(t) складываемых колебаний в произвольный момент времени t, когда фазы этих колебаний соответственно равны и . Сложение колебаний сводится к определению . Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.

Результирующему колебанию соответствует на векторной диаграмме вектор амплитуды и фаза .

Рисунок 2.1 – Сложение сонаправленных колебаний.

Величина вектора А(t) может быть найдена по теореме косинусов:

.

Фаза результирующего колебания задается формулой:

.

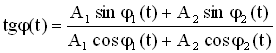
Если частоты складываемых колебаний ω₁ и ω₂ не равны, то и фаза φ(t), и амплитуда А(t) результирующего колебания будут изменяться с течением времени. Складываемые колебания называются некогерентными в этом случае.

2. Два гармонических колебания x₁ и x₂ называются когерентными, если разность их фаз не зависит от времени:

.

Но так как , то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты .

Амплитуда результирующего колебания, полученного при сложении сонаправленных колебаний с равными частотами (когерентных колебаний) равна:

.

Начальную фазу результирующего колебания легко найти, если спроектировать векторы А₁ и А₂ на координатные оси ОХ и ОУ (см. Рисунок 9):

.

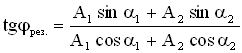
Итак, результирующее колебание, полученное при сложении двух гармонических сонаправленных колебаний с равными частотами, также является гармоническим колебанием .

3. Исследуем зависимость амплитуды результирующего колебания от разности начальных фаз складываемых колебаний.

Если , где n – любое целое неотрицательное число

(n = 0, 1, 2…), то , т.е. результирующая амплитуда будет минимальной. Складываемые колебания в момент сложения находились в противофазе. При результирующая амплитуда равна нулю .

Если , то , т.е. результирующая амплитуда будет максимальной. В момент сложения складываемые колебания находились в одной фазе, т.е. были синфазны. Если амплитуды складываемых колебаний одинаковы , то .

4. Сложение сонаправленных колебаний с неравными, но близкими частотами.

Частоты складываемых колебаний не равны , но разность частот много меньше и ω₁, и ω₂. Условие близости складываемых частот записывается соотношениями .

Примером сложения сонаправленных колебаний с близкими частотами является движение горизонтального пружинного маятника, жесткость пружин которого немного различна k₁ и k₂.

Пусть амплитуды складываемых колебаний одинаковы, а начальные фазы равны нулю . Тогда уравнения складываемых колебаний имеют вид: , .

Результирующее колебание описывается уравнением:

.

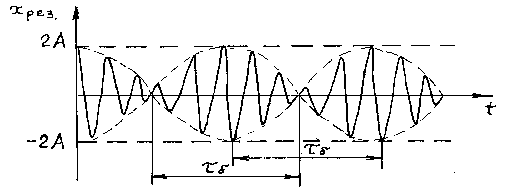
Получившееся уравнение колебаний зависит от произведения двух гармонических функций: одна – с частотой , другая – с частотой , где ω близка к частотам складываемых колебаний (ω₁ или ω₂). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями. Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.

Абсолютное значение косинуса взято потому, что амплитуда – величина положительная. Характер зависимости х_рез.при биениях показан на Рисунке 2.2.

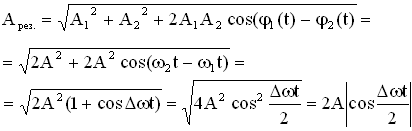
Рисунок 2.2 – Зависимость смещения от времени при биениях.

Амплитуда биений медленно меняется с частотой . Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τ_б, называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения:

.

Величина – период биений.

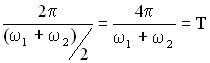
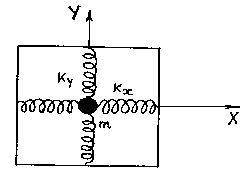
Величина есть период результирующего колебания (Рисунок 2.4).

1. Модель, на которой можно продемонстрировать сложение взаимно перпендикулярных колебаний, представлена на Рисунке 2.3. Маятник (материальная точка массой m) может совершать колебания по осям ОХ и ОУ под действием двух сил упругости, направленных взаимно перпендикулярно.

Рисунок 2.3

Складываемые колебания имеют вид:

.

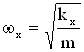
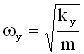
Частоты колебаний определяются как , , где , -коэффициенты жесткости пружин.

2. Рассмотрим случай сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами , что соответствует условию (одинаковые пружины). Тогда уравнения складываемых колебаний примут вид:

Когда точка участвует одновременно в двух движениях, ее траектория может быть различной и достаточно сложной. Уравнение траектории результирующего колебаний на плоскости ОХУ при сложении двух взаимно перпендикулярных с равными частотами можно определить, исключив из исходных уравнений для х и y время t:

.

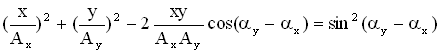
Вид траектории определяется разностью начальных фаз складываемых колебаний, которые зависят от начальных условий (см. § 1.1.2). Рассмотрим возможные варианты.

а) Если , где n = 0, 1, 2…, т.е. складываемые колебания синфазные, то уравнение траектории примет вид:

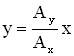
(Рисунок 2.3 а).

б) Если (n = 0, 1, 2 …), т.е. складываемые колебаний находятся в противофазе, то уравнение траектории записывается так:

(Рисунок 2.3б).

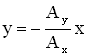
В обоих случаях ( а, б) результирующее движение точки будет колебание по прямой, проходящей через точку О. Частота результирующего колебания равна частоте складываемых колебаний ω₀, амплитуда определяется соотношением:

.

Угол, который прямая (траектория) составляет с осью ОХ, можно найти из уравнения:

(знак “плюс” – случай а, знак “минус” – случай б).

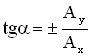
Результатом сложения взаимно перпендикулярных колебаний (случай а и б) является колебание, которое называется линейно поляризованным.

в) Если (n = 0, 1, 2 …), то уравнение траектории результирующего движения примет вид:

.

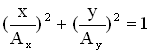
Это уравнение эллипса, его оси совпадают с осями координат ОХ и ОУ, а размеры его полуосей равны и (Рисунок 2.4 ).

Рисунок 2.4

Точка в результате участия в двух взаимно перпендикулярных колебаниях описывает эллипс за время, равное периоду складываемых колебаний .

3. Сложение взаимно перпендикулярных колебаний с кратными частотами.

Складываются взаимно перпендикулярные колебания, частоты которых не равны , но , , где a и b – целые числа.

Периоды колебаний вдоль осей ОХ и ОУ соответственно равны и . Отношение периодов .

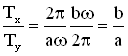
Траектория точки, участвующей во взаимно перпендикулярных колебаниях с кратными частотами, – замкнутая кривая, форма которой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Такие замкнутые траектории называются фигурами Лиссажу.

Под сложением колебаний понимают
нахождение закона результирующих
колебаний системы в тех случаях, когда
эта система одновременно участвует в
нескольких колебательных процессах.
Различают два предельных случая –
сложение колебаний одинакового
направления и сложение взаимно
перпендикулярных колебаний.

Сложение двух одинаково направленных
гармонических колебаний: 
 и 
 можно
произвести, воспользовавшись методом
векторных диаграмм. На рис. 9.1 показаны
векторы А1(t) и А2(t) амплитуд
первого и второго колебаний соответственно
в произвольный момент времени, когда
фазы этих колебаний равны: 
 и 
.
Результирующим колебаниям: 
 соответствует
вектор, проекция которого на вертикальную
ось 
 равна:

 
.                                                                  
                                 (9.1)

По теореме косинусов

 
,                                                       
              (9.2)

 а

 
.                                                           
                    (9.3)

Негармонические колебания, получающиеся
в результате наложения двух одинаково
направленных гармонических колебаний
с близкими частотами 
,
называются биениями. В этом случае
за начало отсчета времени 
 целесообразно
принять тот момент, когда фазы обоих
складываемых колебаний 
 и 
 совпадают
и равны 
.
Тогда 
 и 
,
где 
.
Результирующие колебания удовлетворяют
соотношению

 
,               

47.Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу. Физический смысл спектрального разложения.

Найдем результат сложения двух
гармонических колебаний одинаковой
частоты ω, которые происходят во взаимно
перпендикулярных направлениях вдоль
осей х и у. Начало отсчета для простоты
выберем так, чтобы начальная фаза первого
колебания была равна нулю, и запишем
это в виде 

 (1) 

где
α — разность фаз обоих колебаний, А и В
равны амплитудам складываемых колебаний.
Уравнение траектории результирующего
колебания определим исключением из
формул (1) времени t. Записывая складываемые
колебания как 

 

 

и
заменяя во втором уравнении 
 на 
 и 
 на 
 ,
найдем после несложных преобразований
уравнение эллипса, у которого оси
ориентированы произвольно относительно
координатных осей: 

 (2) 

Фигуры Лиссажу

Отношение частот складываемых колебаний
равно отношению числа пе-

ресечений фигур Лиссажу с прямыми,параллельными
осям координат. По

виду фигур можно определить неизвестную
частоту по известной или определить
отношение частот складываемых колебаний.
Поэтому анализ фигур Лиссажу — широко
используемый метод исследования
соотношений частот и разности фаз
складываемых колебаний, а также формы
колебаний.

Физический смысл

 Рассмотрим для примера
амплитудно-модулированное колебание

f(t) = ( a + 2b cos Ω t
) cos ω t.

     Здесь Ω – частота модуляции, ω –
«несущая» частота, a и b –
постоянные величины. Такое колебание
можно реализовать, например, на входе
радиоприёмника, если радиостанция
работает на частоте ω, а в радиостудии
издаётся звуковой сигнал на частоте Ω.

      Можно видеть, что

( a + 2b cos Ω t ) cos ω t = b cos(ω – Ω)t + a cos ω t + b cos
(ω + Ω) t.

     Что реально существует? Левая
или правая часть этого тождества?

     Если мы принимаем этот сигнал
с помощью радиоприёмника, мы не сможем
сказать, что реально на самом деле:
издаёт ли в радиостудии скрипач звук
на частоте Ω (например, звук «ля») или
работают три генератора на частотах ω –
Ω, ω, ω + Ω. Чтобы это узнать, надо
поехать на студию.

     Однако, если нас интересует,
как действует амплитудно-модулированное
колебание на набор остро настроенных
колебательных контуров, наиболее
целесообразным является представление,
даваемое правой частью тождества. Здесь
целесообразно говорить, что наше
колебание состоит из трёх синусоидальных
колебаний.

     Так в чём же истинное содержание
опытов Ньютона? На основании изложенного
можно сказать, что Ньютон доказал, что
призма есть спектральный прибор, что
она физически выделяет синусоидальные
составляющие, физически осуществляет
спектральное разложение света.
Представление солнечного света в виде
суммы синусоидальных волн является
адекватным, когда мы имеем дело со
спектральной аппаратурой.<p>

     Тем самым может показаться,
что опыты Ньютона с призмой не имеют
фундаментального значения для физики.
Это неверно. Опыты Ньютона показывают,
что солнечный свет действительно
несинусоидален, и позволяют узнать,
каков именно спектр солнечного света.
Из опытов Ньютона мы узнаём, что он
является весьма широким сплошным
спектром, в котором содержатся интенсивные
слагаемые всех видимых цветов, семи
цветов радуги – красного, оранжевого,
жёлтого, зелёного, голубого, синего,
фиолетового

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Для школьников.

Задача.

Даны уравнения одинаково направленных колебаний материальной точки:

Надо получить уравнение результирующего колебания точки.

Решение. Из уравнений видно, что складываемые колебания имеют одинаковую частоту, равную 5 рад/с.

Амплитуда результирующего колебания (см. рис 25):

Находим начальную фазу результирующего колебания точки:

отсюда

Тогда уравнение результирующего колебания имеет вид:

Таким образом, если материальная точка одновременно участвует в двух гармонических колебаниях одинаковой частоты и одного направления, то её результирующее колебание тоже будет гармоническим с той же частотой.

Если же материальная точка участвует одновременно в двух гармонических колебаниях одного направления, но частоты этих колебаний разные, то результирующее колебание уже не будет гармоническим (синусоидальным). Покажем это на рисунке.

Здесь пунктирными линиями показаны графики двух гармонических колебаний разных частот, в которых участвует материальная точка (горизонтальная линия соответствует её положению равновесия).

Алгебраическое сложение смещений в каждом из двух колебаний (в данный момент времени) даёт результирующее смещение материальной точки от её положения равновесия (АD = АВ + АС).

По полученным в результате сложения точкам построен график суммарного колебания материальной точки (сплошная линия), форма которой не является синусоидой.

Сплошная линия на рисунке есть график негармонического периодического суммарного колебания (его ещё называют формой периодического колебания или просто формой).

Период суммарного колебания (формы) равен периоду гармонического колебания с наиболее низкой частотой, называемой основной частотой (см. рисунок).

Определённой частоты у суммарного колебания нет.

Теперь рассудим наоборот. Пусть известна форма, т. е. график колебаний материальной точки (сплошная линия на рисунке).

Это сложное периодическое колебание (форму) можно разложить на набор гармонических колебаний (в рассматриваемом случае их два). В других случаях этот набор может включать в себя много гармонических колебаний (гармоник).

В этом заключается смысл теоремы Фурье: всякое периодическое колебание периода Т может быть представлено в виде суммы гармонических колебаний с периодами, равными T, Т/2, Т/3, Т/4 и т. д., т. е. с частотами, равными 1/Т, 2/Т, 3/Т, 4/Т и т. д.

Каждое из набора колебаний имеет определённую частоту.

Самая низкая (малая) частота называется основной частотой.

Частоты других гармонических колебаний (гармоник), на которые разложили периодическое сложное колебание (форму), в 2, 3, 4 и т. д. раз больше основной частоты.

Они называются второй, третьей, четвёртой и т. д. гармониками (высшими гармониками).

Такое действие – разложение сложного периодического колебания (формы) в гармонический ряд (на гармонические колебания) часто бывает нужно на практике и называется оно гармоническим анализом.

Гармонический анализ позволяет детально описать и проанализировать любой колебательный процесс.

С периодическими колебаниями (формами) мы встретимся ещё при рассмотрении звуковых колебаний.

Если частоты складываемых гармонических колебаний одного направления близки друг другу, то получается интересная картина.

Итак, нами рассмотрены примеры сложения гармонических колебаний. Говоря о сложении гармонических колебаний одного направления, но разных частот, приходим к выводу, что результирующее колебание (форма) уже не является гармоническим, но является периодическим. И ещё приходим к заключению, что любое сложное колебание можно разложить на совокупность гармонических колебаний (гармоник). Этим разложением, называемым гармоническим анализом, широко пользуются на практике.

https://yandex.ru/video/preview/?text=%D0%B4%D0%B5%D0%BC%D0%BE%D0%BD%D1%81%D1%82%D1%80%D0%B0%D1%86%D0%B8%D1%8F%20%D1%81%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5%20%D0%B3%D0%B0%D1%80%D0%BC%D0%BE%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85%20%D0%BA%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D0%B9&path=wizard&parent-reqid=1638617385109896-9444507951277324299-sas3-0841-245-sas-l7-balancer-8080-BAL-7543&wiz_type=vital&filmId=6200809953460406703

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Пример нахождения характеристик гармонического колебания материальной точки.

Следующая запись: Затухающие колебания.

Ссылки на занятия до электростатики даны в Занятии 1 .

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .

Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 5 8.

Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .