Частота среза ачх как найти

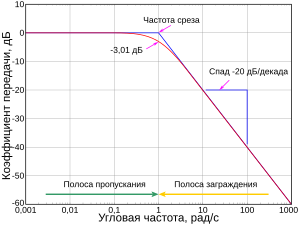
Пример ЛАЧХ фильтра Баттерворта 1-го порядка^[1] с отмеченной частотой среза −3 дБ.

Верхняя ( $f_{2}$ ) и нижняя ( f_1 ) частоты среза некоторого полосового фильтра.

Частота́ сре́за (частота отсе́чки) $f_{c}$ — частота, выше или ниже которой мощность выходного сигнала некоторого линейного частотно-зависимого объекта, например, электронной схемы, уменьшается в два раза^[2] от мощности в полосе пропускания при воздействии на вход неизменного по амплитуде сигнала.

Амплитудно-частотная характеристика на частоте среза имеет спад до уровня ${displaystyle -log _{10}2}$ (приблизительно −3 дБ) относительно уровня в полосе пропускания.

Содержание

1 Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка
2 См. также
3 Примечания
4 Ссылки

Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка[править | править код]

Фильтр нижних частот (ФНЧ) 1-го порядка имеет комплексную передаточную функцию H(s) вида:

${displaystyle H(s)={frac {1}{1+alpha s}},}$

где

— комплексная переменная преобразования Лапласа;

— параметр фильтра, константа.

В случае подачи на вход фильтра гармонического сигнала с частотой omega в установившемся режиме комплексная передаточная функция имеет вид:

${displaystyle H(jomega )={frac {1}{1+alpha jomega }},}$

где буквой

обозначена мнимая единица;

— угловая частота.

Эта функция имеет единственный полюс (частота, при которой знаменатель дроби обращается в 0) на частоте ${displaystyle omega _{c}=2pi f_{c}=1/{alpha },}$ $f_{c}$ — частота среза.

Модуль коэффициента передачи этого ФНЧ в зависимости от частоты (эту функцию принято называть амплитудно-частотной характеристикой) имеет вид:

${displaystyle left|H(jomega )right|=left|{frac {1}{1+alpha jomega }}right|={sqrt {frac {1}{1+alpha ^{2}omega ^{2}}}}.}$

Модуль коэффициента передачи на частоте полюса:

${displaystyle left|H(jomega _{mathrm {c} })right|={sqrt {frac {1}{1+alpha ^{2}omega _{mathrm {c} }^{2}}}}={frac {1}{sqrt {2}}}.}$

То есть, на частоте полюса коэффициент передачи уменьшается в В рассмотренном примере частота среза равна частоте полюса.

См. также[править | править код]

Фильтр нижних частот
Фильтр верхних частот
Постоянная времени
Круговая частота

Примечания[править | править код]

↑ Порядок фильтра равен порядку (степени алгебраического уравнения) знаменателя передаточной функции (ЛАФЧХ) фильтра. Как правило^{[уточнить]}, порядок фильтра равен количеству входящих в него сосредоточенных реактивных элементов.
↑ При этом амплитуда сигнала на частоте среза равна ${displaystyle {frac {1}{sqrt {2}}}approx 0,707}$ от амплитуды сигнала в полосе пропускания.

Ссылки[править | править код]

Преобразование частоты среза f_c и постоянной времени τ (англ.)
Основные характеристики и параметры фильтров

Это статья-заготовка об электронике. Помогите Википедии, дополнив эту статью, как и любую другую.

Источник

Частота среза

Частота среза
определяется как частота, на которой
значение АЧХ фильтра падает до 1/=
0.707 от своей величины в полосе
пропускания. Она также называется
«точкой 3 дБ» (поскольку 20lg (0.707) = -3).

Полоса пропускания, полоса задерживания и переходная полоса

Полоса пропускания
– это частотная область, внутри которой
сигналы проходят сквозь фильтр фактически
без затухания. Полоса
задерживания
выбирается проектировщиком такой, чтобы
обеспечить уровень затухания не ниже
заданного. Частотную область между
точкой 3 дБ и полосой задерживания
называют переходной
полосой.
Переходная полоса характеризуется
своей скоростью спада, которая обычно
выражается в дБ/декада.

Пульсации

АЧХ некоторых
фильтров имеют пульсации как в полосе
пропускания, так и в полосе задерживания.
Пульсации в полосе пропускания более
значимы, поскольку они вносят определенные
искажения в интересующий нас сигнал.
Некоторый уровень пульсаций в полосе
пропускания бывает допустимым, это
зависит от конкретной задачи. Можно
проектировать фильтры с произвольным
уровнем пульсаций, но, как правило, имеет
место компромисс между уровнем пульсаций
в полосе пропускания, скоростью спада
в переходной полосе и затуханием в
полосе задерживания.

Требования к характеристикам фильтра:

пульсации в полосе
пропускания,
скорость спада в
переходной полосе,
затухание в полосе
задерживания,
ФЧХ (наша следующая
тема).

ФЧХ

Вид ФЧХ является
одним из важнейших показателей фильтра
при принятии решения о его пригодности
для конкретного приложения. ФЧХ позволяет
определить временную задержку, вносимую
в сигнал.

Линейная и нелинейная фчх

Фильтр с линейной
ФЧХ задерживает все частоты на одно и
то же время. Следовательно, выходной
сигнал не искажается, а лишь задерживается
на соответствующее время. Поскольку
реальный сигнал содержит много частот,
задержка каждой частоты на разное время
приводит к искажению выходного сигнала.

В некоторых
приложениях, таких как музыка или видео,
нелинейная ФЧХ недопустима.

Линейная ФЧХ
исключительно важна в полосе пропускания,
поскольку тот диапазон, в котором
происходит выделение интересующих нас
частотных составляющих сигнала. Обычно
имеет место компромисс между линейной
ФЧХ в полосе пропускания и другими
требованиями к фильтру, такими как
крутизна спада и затухание в полосе
задерживания.

Практически используемые аналоговые фильтры

Существует много
схем аналоговых фильтров с различными
характеристиками АЧХ и ФЧХ. Рассмотрим
более подробно фильтр Баттерворта.

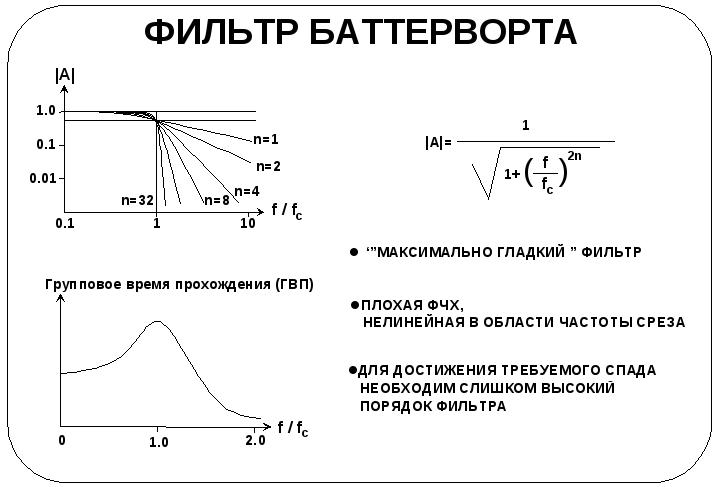
Фильтр Баттерворта

Этот тип фильтра
обычно называют «максимально гладким»
вследствие плавности АЧХ в полосе
пропускания. У фильтров Баттерворта
действительно нет пульсаций в полосе
пропускания, однако им присущи два
недостатка:

1. Нелинейная ФЧХ
в полосе пропускания исключает их
применение в тех приложениях, где
требуется линейная ФЧХ. График группового
времени прохождения (ГВП)^{^}⁾
в нормированной шкале частот иллюстрирует
нелинейность ФЧХ. Ненормированная
частота среза при этом равна f/f_c
= 1.0. Задержка, вносимая в сигнал,
существенно увеличивается, когда
значение нормированной частоты
приближается к частоте среза.

2. В переходной
полосе АЧХ фильтра Баттерворта имеет
пологий спад. Для того, чтобы достичь
заданной крутизны спада, потребуется
каскадное соединение большого числа
звеньев. На графике представлено
семейство АЧХ для фильтров Баттерворта
различного порядка.

Источник

Фильтры нижних и высших частот

Фильтр нижних частот (ФНЧ) – электрическая цепь, эффективно пропускающая частотный спектр сигнала ниже определённой частоты, называемой частотой среза, и подавляющая сигнал выше этой частоты.

Фильтр высших частот (ФВЧ) – электрическая цепь, эффективно пропускающая частотный спектр сигнала выше частоты среза, и подавляющая сигнал ниже этой частоты.

Рассмотрим в качестве фильтра простейшую цепь RC, принцип работы которой основан на зависимости реактивного сопротивления конденсатора от частоты сигнала.

Если к источнику переменного синусоидального напряжения U частотой f подключить последовательно резистор сопротивлением
R и конденсатор ёмкостью C, падение напряжения на каждом из элементов можно вычислить
исходя из коэффициента деления с импедансом Z.

Импеданс – комплексное (полное) сопротивление цепи для гармонического сигнала.
Z² = R² + X² ; Z = √(R² + X²) , где Х – реактивное сопротивление.

Тогда на выводах резистора напряжение U_R будет составлять:

X_C – реактивное сопротивление конденсатора, равное 1/2πfC

При равенстве R = X_C на частоте f, выражение упростится сокращением R и примет вид:

Следовательно, на частоте f равенство активного и реактивного сопротивлений цепочки RC обеспечит
одинаковую амплитуду переменного синусоидального напряжения на каждом из элементов в √2 раз меньше входного напряжения,
что составляет приблизительно 0.7 от его значения.
В этом случае частота f определится исходя из сопротивления R и ёмкости С выражением:

τ – постоянная времени цепи RC равна произведению RC

Повышение частоты уменьшит реактивное сопротивление конденсатора и падение напряжение на нём, тогда напряжение на выводах резистора возрастёт.
Соответственно, понижение частоты увеличит напряжение на конденсаторе и уменьшит на резисторе.

Зависимость амплитуды переменного напряжения от его частоты называют амплитудно-частотной характеристикой (АЧХ).

Если рассмотреть АЧХ напряжения на выводах конденсатора или резистора в RC цепи, можно наблюдать на частоте f = 1/(2π τ)
спад уровня до значения 0.7, что соответствует -3db по логарифмической шкале.

Следовательно, цепь RC может быть использована как фильтр нижних частот (ФНЧ) – красная линия на рисунке, или фильтр высших частот (ФВЧ) – синяя линия.

Ниже представлены схемы включения RC-цепочек в качестве фильтров соответственно ФНЧ и ФВЧ.

Частоту f = 1/(2π τ) называют граничной частотой f_гр или частотой среза f_ср фильтра.

Частоту среза фильтра можно посчитать с помощью онлайн калькулятора

Достаточно вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Пост. времени τ RC и частота среза RC-фильтра
τ = RC ; f_ср = 1/(2πτ)

Замечания и предложения принимаются и приветствуются!

Источник

Частота среза на диаграмме Найквиста

Добавлено 22 февраля 2020 в 23:21

Данная статья продолжает наше исследование диаграммы Найквиста, рассматривая взаимосвязь между кривой графика и частотой среза фильтра.

В предыдущей статье мы видели, что частотная характеристика системы может быть представлена графиком в полярной системе координат, на котором кривая показывает амплитуду и фазу при изменении частоты от нуля до бесконечности. Мы называем его графиком Найквиста (или диаграммой Найквиста), и это интересная альтернатива гораздо более распространенному графику Боде (логарифмическим амплитудно-частотной и фазо-частотной характеристикам).

Следующая диаграмма была представлена в конце предыдущей статьи и дает хороший визуальный обзор основной информации, которую мы можем извлечь из графика Найквиста для фильтра первого порядка.

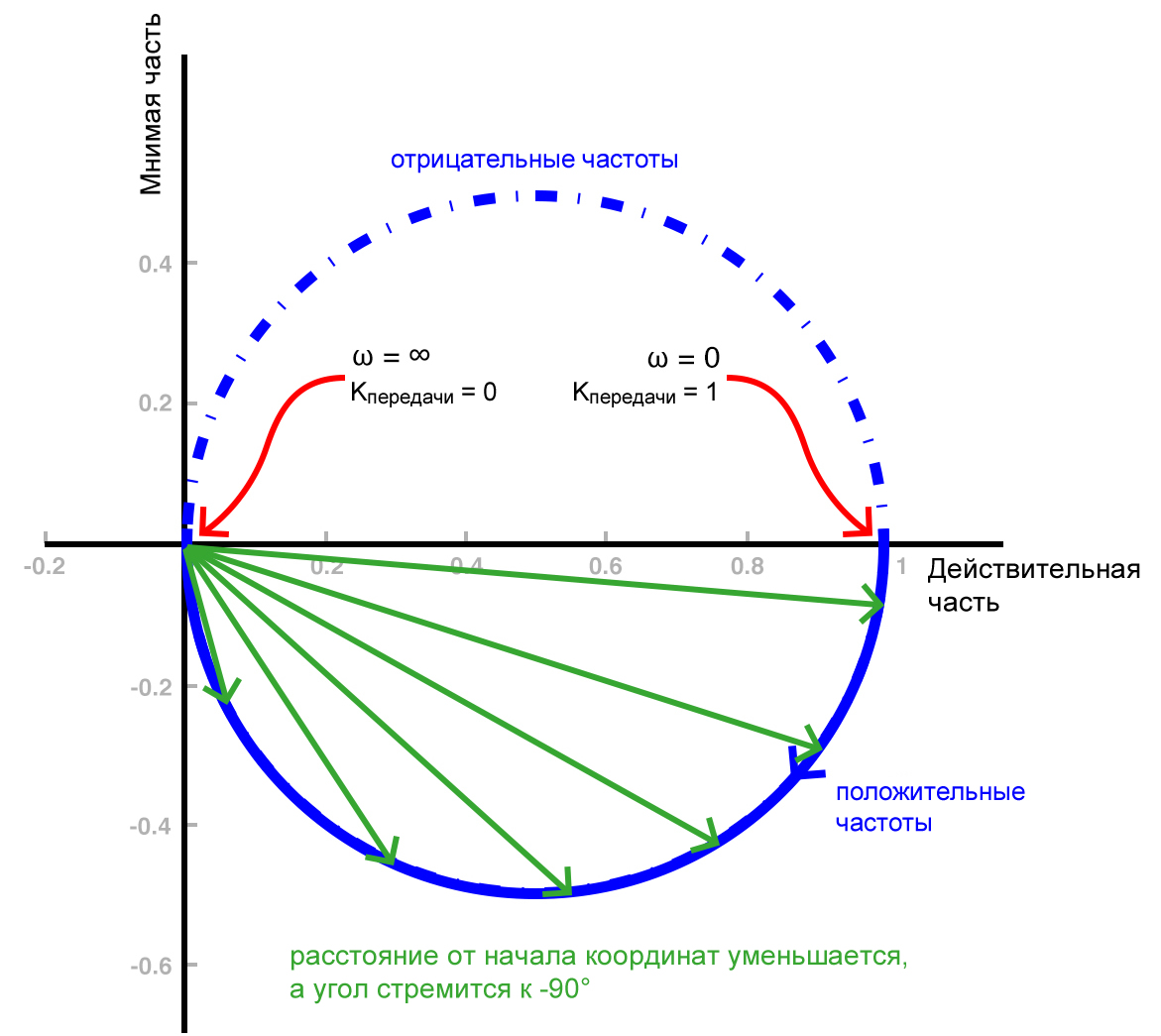
Рисунок 1 – Пояснения к диаграмме Найквиста

Важность частоты среза

Приведенная выше диаграмма не включает в себя одну очень важную деталь, а именно, частоту среза фильтра. Передаточная функция в s-области для фильтра нижних частот первого порядка может быть выражена следующим образом:

[T(s)=frac{K}{1+left(frac{s}{omega _{0}}right)}]

Эта формула говорит нам, что единственными отличительными характеристиками данного фильтра нижних частот являются K и ω₀. Параметр K – это коэффициент усиления фильтра при постоянном напряжении. Пассивные компоненты не способны усиливать сигнал, поэтому, если мы имеем дело только с RC фильтрами нижних частот первого порядка, мы можем игнорировать K, потому что он всегда будет равен 1. Оставшийся параметр ω₀ – это частота среза. Таким образом, мы можем полностью описать RC фильтр нижних частот, просто указав частоту среза.

Определение частоты среза

Кривая на диаграмме Найквиста, конечно, не имеет типового спада характеристики, который мы хорошо знаем из графиков амплитудно-частотных характеристик, и фактически график Найквиста не дает нам конкретной информации о частоте среза схемы фильтра. Однако изучение взаимосвязи между частотой среза и кривой Найквиста является хорошим способом укрепить понимание концепции частоты среза в целом, а также даст нам некоторое представление об ограничениях подхода Найквиста для визуального изображения частотной характеристики.

Во-первых, нам нужно подумать о том, что на самом деле происходит на частоте среза, с точки зрения как амплитудно-частотной, так и фазо-частотной характеристики.

Частота среза относительно амплитуды

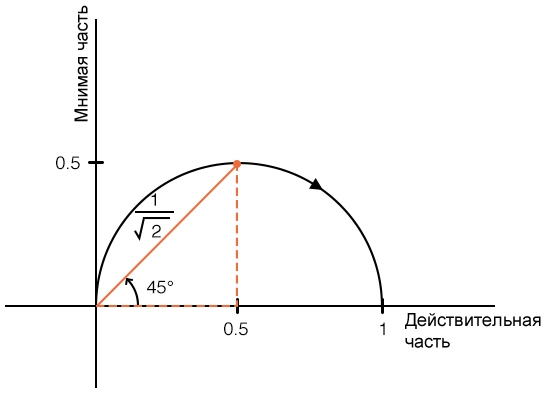
Вы, вероятно, знаете, что другое название для частоты среза – это «частота 3 дБ» (или –3 дБ), и это напоминает нам о том, что фильтр нижних частот первого порядка обеспечивает ослабление на 3 дБ (или, что эквивалентно, усилению –3 дБ), когда входная частота равна ω₀. Мы не используем децибелы на графике Найквиста, поэтому вместо –3 дБ мы используем соответствующий коэффициент передачи в разах, который равен (frac{1}{sqrt{2}})

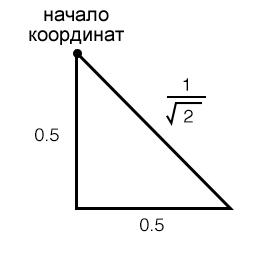
Когда мы работаем с графиком в полярной системе координат, мы всегда должны помнить о треугольниках; например, амплитуда (модуль) комплексного числа определяется как гипотенуза прямоугольного треугольника, два катета которого являются действительной и мнимой частями; а для вычисления фазы (угла) комплексного числа мы используем тригонометрические функции. Теперь, когда вы думаете с точки зрения треугольников, коэффициент (frac{1}{sqrt{2}}) дает вам какие-нибудь идеи?

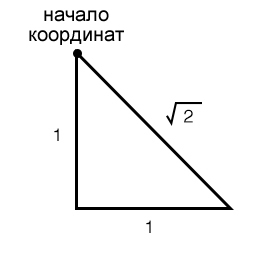
Рисунок 2 – Прямоугольный треугольник. Длина катетов равна 1

Как показано выше, коэффициент (sqrt{2}) вступает в игру всякий раз, когда у прямоугольного треугольника два катета равной длины. Если уменьшить длину катетов до 0,5, длина гипотенузы будет равна (sqrt{2} times 0,5), что то же самое, что (frac{1}{sqrt{2}}).

Рисунок 3 – Прямоугольный треугольник. Длина катетов равна 0,5

Итак, что же всё это значит? Рассмотрим следующий график Найквиста:

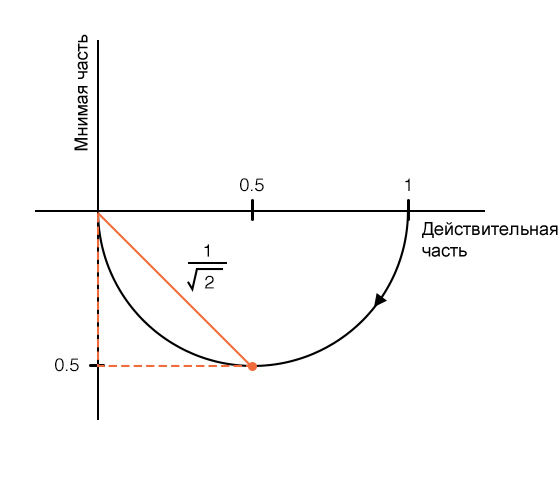
Рисунок 4 – Это график Найквиста для фильтра нижних частот первого порядка. Обратите внимание, что я не добавил часть графика, которая соответствует отрицательным частотам.

Как видите, в самой нижней точке кривой коэффициент усиления фильтра равен (frac{1}{sqrt{2}}), где абсолютное значение действительной части равно абсолютному значению мнимой части; это и есть местоположение частоты среза на графике Найквиста для фильтра нижних частот первого порядка. То же самое отношение применяется к фильтру верхних частот первого порядка, за исключением того, что в этом случае частота среза находится в самой высокой точке кривой:

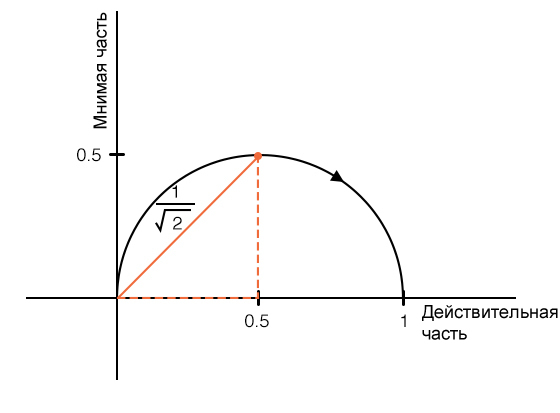
Рисунок 5 – Частота среза фильтра верхних частот первого порядка на диаграмме Найквиста

Разница заключается в том, что сдвиг фазы фильтра верхних частот с увеличением частоты изменяется от +90° до 0°, тогда как фаза фильтра нижних частот изменяется от 0° до –90°. Поскольку угол измеряется против часовой стрелки от положительной действительной оси, положительный сдвиг фазы отображается над действительной осью, а отрицательный сдвиг фазы отображается ниже действительной оси.

Также обратите внимание, что на этих двух графиках есть стрелки, указывающие в противоположных направлениях: на графике фильтра нижних частот стрелка указывает на начало координат, поскольку с увеличением частоты коэффициент усиления уменьшается; на графике фильтра верхних частот она указывает в сторону от начала координат, поскольку с увеличением частоты коэффициент усиления увеличивается.

Частота среза относительно сдвига фазы

Мы также можем найти частоту среза на графике Найквиста, если вспомнить, что сдвиг фазы на 90°, создаваемый фильтром первого порядка, центрирован относительно частоты среза. Другими словами, фазовый сдвиг при ω₀ составляет +45° или –45°. Вектор, нарисованный в комплексной плоскости, будет иметь угол +45° или –45°, если его действительная и мнимая части имеют одинаковые абсолютные значения, и это приводит нас к тем же геометрическим соотношениям, которые мы обнаружили при рассмотрении частоты среза с точки зрения амплитуды отклика.

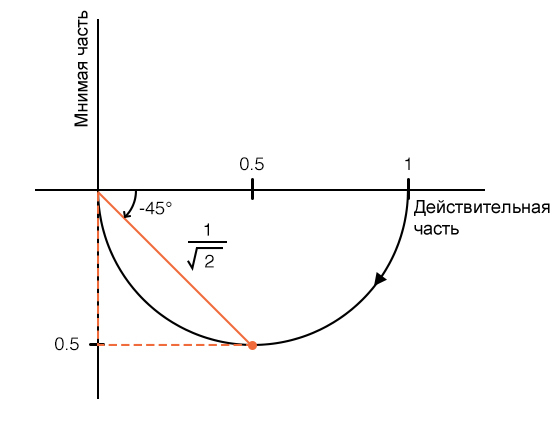
Рисунок 6 – Частота среза фильтра нижних частот первого порядка на диаграмме Найквиста

Рисунок 7 – Частота среза фильтра верхних частот первого порядка на диаграмме Найквиста

Заключение

Возможно, вы заметили, что расположение частоты среза на этих графиках Найквиста является чисто геометрическим. Вы не можете прикрепить фиксированное значение частоты к этому местоположению, так как это местоположение одинаково для каждого фильтра нижних частот первого порядка или для каждого фильтра верхних частот первого порядка. Диаграмма Найквиста явно не является заменой для обычных логарифмических амплитудно-частотной и фазо-частотной характеристик. Но тем не менее, она дает более прямой способ передачи информации о передаточной функции системы, и, как мы увидим в следующей статье, это удобный инструмент для анализа устойчивости (стабильности).

Эти понятия относятся к теории автоматического управления. Частота среза используется при анализе устойчивости системы управления. Чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы фаза разомкнутой системы не достигала −180° на частоте среза.

Частота среза имеет другое определение в обработке сигналов. Там под частотой среза подразумевают частоту сопряжения, а понятием частота сопряжения не пользуются. В обработке сигналов нет необходимости анализировать устойчивость системы.

Понятия раскрываются в книге Бесекерского и Попова «Теория систем автоматического регулирования» 2003 года. Приведу пару цитат, где вводятся эти понятия.

Первая цитата со страницы 59:

Точку пересечения прямой с осью нуля децибел (осью частот) можно найти, положив L(ω)=0 или, соответственно, A(ω)=1. Отсюда получаем так называемую частоту среза л. а. х.,

При этом в книге частота среза обозначается как ω_ср.

На странице 66 описывается апериодическое звено первого порядка:

Наиболее просто, практически без вычислительной работы, строится так называемая асимптотическая л. а. х. На стандартной сетке проводится вертикальная прямая через точку с частотой, называемой сопрягающей частотой ω=1/T.

При чем эта «вертикальная прямая» проводится в точке изменения наклона частотной характеристики.

Скриншот этой страницы с полным описанием:

Источник

Содержание

Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]