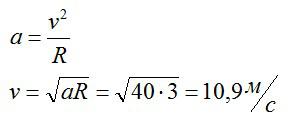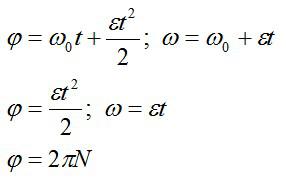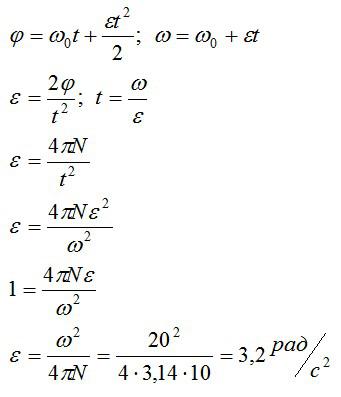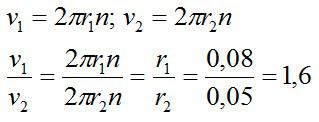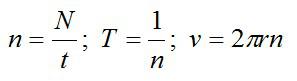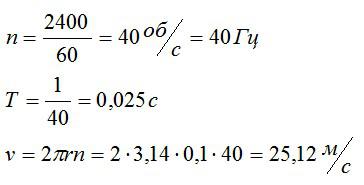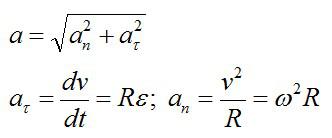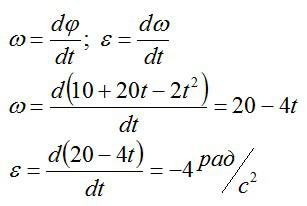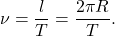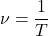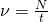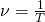Пример решения задачи по определению числа оборотов колеса маховика вращающегося равномерно с заданной угловой скоростью за время вращения t=5 минут.
Задача
Маховое колесо вращается равномерно с угловой скоростью 16 с-1.
Определить, сколько оборотов сделает колесо за 5 мин вращения.
Другие примеры решений >
Помощь с решением задач >
Решение
Рассмотрим два варианта решения задачи:
1) Находим угол поворота маховика в радианах (t = 5 мин =300 с):
Находим число оборотов маховика:
2) Возможно другое решение. Переведем угловую скорость в об/мин:
Уравнение равномерного вращательного движения можно представить так: N = nt, где N — в оборотах, n — об/мин и t — в мин.
Находим число оборотов маховика:
Другие примеры решения задач >>
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Лень разбираться с решением задач? Добро пожаловать к нам в телеграм, где собрана интересная и полезная информация для учащихся и не только.
Движение по окружности: определение, примеры
Движение по окружности – самый простой случай криволинейного движения.
Примеры движения по окружности:
- грузовик движется по мосту с радиусом кривизны R;
- атлет крутит шар в руке, перед тем как бросить его;
- космическая станция летает по кругу над поверхностью Земли;
- катафот вращается на раскрученном колесе велосипеда.
Приведем ниже кинематические соотношения для поступательного и вращательного движений:
Вопросы на движение по окружности
Вопрос 1. Как направлено центростремительное ускорение?
Ответ. Центростремительное ускорение направлено по радиус-вектору к центру окружности.
Вопрос 2. Велосипед катится по прямой. Как можно описать движение точки на ободе его колеса? Является ли это движение движением по окружности?
Ответ. Это одновременно поступательное движение и движение по окружности. Траекторией такого движения будет спираль.
Вопрос 3. Как направлено ускорение, если тело движется по окружности неравномерно?
Ответ. В таком случае к центростремительному (или нормальному) ускорению добавляется тангенциальное ускорение, направленное по касательной к окружности. Полное ускорение тела представляет собой векторную сумму тангенциального и нормального ускорений.
Вопрос 4. Что такое линейная и угловая скорость?
Ответ. Линейная скорость – это скорость точки, движущейся поступательно. Она измеряется в метрах в секунду. Угловая скорость – скорость, с которой меняется угол, на который поворачивается радиус-вектор точки при движении по окружности.
Вопрос 5. При поступательном движении мерой инерции является масса. А что является мерой инерции при вращательном движении?
Ответ. При вращательном движении мерой инерции является момент инерции. Это отдельная обширная тема, задачи на нахождение и использование момента инерции рассмотрены в других статьях по физике.
Задачи на движение по окружности
Как решать задачи на движение по окружности? Так же, как и все остальные! Для начала, вот памятка по решению физических задач и полезный список формул. Кстати! Для всех наших читателей действует скидка 10% на любой вид работы.
Задача №1. Нахождение линейной скорости при движении по окружности
Условие
Тело движется по окружности с ускорением 3 метра на секунду в квадрате по окружности радиусом 40 метров. Какова линейная скорость тела?
Решение
В данном случае ввиду имеется нормальное ускорение. Поэтому, для решения достаточно вспомнить всего одну формулу:
Ответ: 10,9 м/с.
Задача №2. Нахождение углового ускорения
Условие
Колесо, вращаясь с постоянным ускорением, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.
Решение
Запишем закон вращения, учитывая, что по условию начальная угловая скорость равна нулю:
Выразим угловое ускорение из первого уравнения, а время – из второго. Затем подставим выраженное время в выражение для ускорения и сократим:
Ответ: 3,2 радиан на секунду в квадрате.
Чтобы перевести угол из радианов в градусы достаточно запомнить соотношение: в одном полном обороте 2пи радиан, или 360 градусов. Следовательно, в одном радиане примерно 57,3 градуса.
Задача №3. Нахождение скорости движения по окружности
Условие
Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Решение
Две точки вращаются на одном колесе, а значит, с одинаковой частотой. Используем соотношения для скорости:
Ответ: скорость точки на ободе больше в 1,6 раза.
Задача №4. Нахождение периода и частоты при движении по окружности
Условие
Маховик равномерно вращается и за время t=1 мин совершает N=2400 оборотов. Какова частота вращения маховика, период обращения и линейная скорость точки, расположенной на расстоянии 10 сантиметров от центра маховика?
Решение
По определению:
Подставим значения, предварительно переведя все величины в систему СИ, и вычислим:
Ответ: 40 Гц; 0,025 с; 25,12 м/с.
Задача №5. Нахождение полного ускорения при движении по окружности
Условие
Тело вращается вокруг стационарной оси по закону фи=10+20t-2t^2. Нужно найти полное ускорение точки, находящейся на расстоянии 10 см от оси вращения в момент времени t=4c.
Решение
Полное ускорение – векторная сумма нормального и тангенциального ускорений.
Вспоминаем, что скорость и ускорение можно вычислить через производные, зная закон движения:
Подставляем значение t из условия и вычисляем:
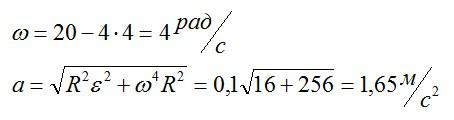
Ответ: 1,65 метра в секунду.
Нужна помощь в выполнении заданий? Обращайтесь в профессиональный студенческий сервис в любое время.
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Движение по окружности, период обращения и частота.
1. Равномерное движение по окружности
Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.
Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.
Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.
Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке.
Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.
2. Период вращения и вращающаяся частота
Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.
Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.
Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.
При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:
Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: 
Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:
частота вращения равна количеству полных оборотов за одну секунду.
Частота вращения и период обращения связаны следующим соотношением:
Частоту в СИ измеряют в
3. Вращательное движение
В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.
Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.
Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.
ПРОВЕРЬТЕ СЕБЯ
- Приведите два-три примера криволинейного движения.
- Приведите два-три примера равномерного движения по кругу.
- Что такое вращательное движение? Приведите примеры такого движения.
- Как направлена мгновенная скорость при движении по кругу Приведите два-три примера.
1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.
2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: 
3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.
[spoiler title=”источники:”]
http://repetitor.org.ua/dvizhenie-po-okruzhnosti-period-obrashheniya-i-chastota
[/spoiler]
Частота вращения (обращения) — это физическая величина, равная количеству оборотов, которые тело совершает за единицу времени (1 секунду).
Чтобы найти частоту вращения надо количество оборотов разделить на время совершения этих оборотов:
Частота вращения – величина, обратная периоду вращения:
Частота вращения показывает, сколько оборотов совершается за 1 с.
За единицу частоты вращения в СИ принимают частоту вращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: [1/с] или [с-1] (читается: секунда в минус первой степени). Единица частоты в СИ называется Герц [Гц].
Обозначения:
T — период обращения
ν — частота обращения
N — число оборотов
t — время, за которое тело совершило N оборотов по окружности
Если
угловая скорость постоянна (ω
= const), то
вращение называется равномерным,
при этом угловое перемещение тела
или
.
(8.5)
В
технике скорость равномерного вращения
часто определяют числом оборотов в
минуту, обозначая эту величину через
n, об/мин.
Существует
зависимость между n
и ω.
При одном обороте тело поворачивается
на угол 2π,
а при n
оборотах − на 2πn;
этот поворот делается за t
= 1мин = 60 с.
Из равенства (8.5) следует, что
.
(8.6)
Если
угловое ускорение тела постоянно (ε
= const), то
вращение называется
равнопеременным.
Найдём закон равнопеременного вращения,
считая, что в начальный момент времени
t0
= 0
угол φ0
= 0,
а угловая скорость ω
= ω0
(ω0
– начальная угловая скорость).
Из
формулы (8.4) имеем dω
= εdt.
Интегрируя левую часть от ω0
до ω,
а правую часть – в пределах от 0
до t,
найдём:
.
(8.7)
Представим
данное выражение в виде
или
.
Вторично
интегрируя, найдём закон равномерного
вращения:
.
(8.8)
Угловая
скорость этого вращения определяется
формулой (8.7). Если величины ω
и ε
имеют одинаковые знаки, то вращение
будет равноускоренным,
а если разные – равнозамедленным.
8.2.2. Скорости и ускорения точек вращающегося тела
Рассмотрим
какую-нибудь точку М
твёрдого тела, находящуюся на расстоянии
ρ
от оси вращения Az
(см.
рис. 8.2).
При вращении тела точка М
будет описывать окружность радиуса ρ,
плоскость которой перпендикулярна к
оси вращения, а центр С
лежит на самой оси. За время dt
произойдёт элементарный поворот тела
на угол dφ,
а точка М
совершит вдоль своей траектории
элементарное перемещение
.
Тогда скорость точки будет равна
.
(8.9)
Скорость
v
в отличие от угловой скорости тела
называют линейной
или
окружной скоростью точки
М.
Т
аким
образом,
линейная скорость точки вращающегося
твёрдого тела численно равна произведению
угловой скорости тела на расстояние от
этой точки до оси вращения.
Направлена
линейная скорость по касательной к
описываемой точкой М
окружности или перпендикулярно к
плоскости II,
проходящей через ось вращения и точку
М.
Т
ак
как для всех точек тела угловая скорость
ω
имеет в данный момент одно и то же
значение, то из формулы (8.9) следует, что
линейные скорости точек вращающегося
тела пропорциональны их расстояниям ρ
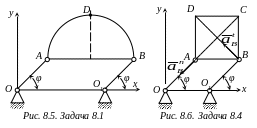
от оси вращения (рис.
8.4).
Для
определения ускорения точки М
воспользуемся формулами:
,
.
Подставляя
значение v
из равенства (8.9), получим
.
(8.10)
Касательное
(тангенциальное)
ускорение
направлено по касательной к траектории
(в сторону движения, если тело вращается
ускоренно, или в обратную сторону, если
тело вращается замедленно); нормальное
ускорение
всегда направлено по радиусу ρ
к оси вращения (рис.
8.4).
Полное
ускорение точки М
равно
.
(8.11)
Отклонение
вектора полного ускорения от радиуса
описываемой точкой окружности определяется
углом μ,
который находят по формуле
.
(8.12)
Из
формул (8.11) и (8.12) следует, что
ускорения всех точек вращающегося
твёрдого тела пропорциональны их
расстояниям от оси вращения и образуют
в данный момент времени один и тот же
угол μ
с радиусами описываемых ими окружностей.
Формулы
(8.9)…(8.12) позволяют определять скорость
и ускорение любой точки тела, если
известен закон вращения тела и расстояние
данной точки от оси вращения.
Простейшими
движениями твёрдого тела являются
поступательное
и вращательное движения.
Изучение
поступательного движения точки сводится
к задаче кинематики точки.
Основными
кинематическими характеристиками
вращательного движения твёрдого тела
являются его угловая скорость и угловое
ускорение. Вращение твёрдого тела может
быть равномерным и равнопеременным,
равноускоренным
и равнозамедленным.
Линейные
скорости и ускорения всех точек
вращающегося тела пропорциональны их
расстояниям от оси вращения. Линейные
скорости образуют прямой угол с радиусом
описываемой окружности, а ускорения −
некоторый угол, определяемый формулой
(8.12).
Задачи для
самостоятельного решения
З
адача
№ 8.1.
(Рис.
8.5).
При
вращении кривошипа OA
= О1В
= 0,16
м
угол φ
изменяется по закону φ
=
π t.
Определить
радиус r
кривизны траектории точки D
полукруга
ABD
при
t
= 2 с,
если АВ
= 0,25 м.
(Ответ:
r
=
0,16
м).
Задача
№ 8.2.
(Рис.
8.5).
При
вращении кривошипа OA
= О1В
= 0,10
м
угол φ изменяется по закону φ
=
2π t.
Определить
скорость vD
точки D
полукруга
ABD
при
t
= 2 с,
если АВ
= 0,25 м.
(Ответ:
vD
=
0,63
м/с).
Задача
№ 8.3. (Рис.
8.5).
При
вращении кривошипа OA
= О1В
= 0,10
м
угол φ
изменяется по закону φ
=
4π t.
Определить
ускорение аD
точки D
полукруга
ABD
при
t
= 2 с,
если АВ
= 0,25 м.
(Ответ:
аD
=
15,8
м/с2).
Задача
№ 8.4.
(Рис. 8.6).
Квадратная
пластина ABCD
совершает
поступательное движение в плоскости
Оху.
Определить
ускорение аС
точки С,
если
известно, что нормальное ускорение
точки
А,
а касательное ускорение точки
В
.
(Ответ:
ас
=
5
м/с2).
Задача
№ 8.5.
При
равномерном вращении маховик делает 4
оборота в секунду. За сколько секунд
маховик повернется на угол φ
= 24
π?
(Ответ:
3
с).
Задача
№ 8.6.
Угловая
скорость тела изменяется согласно
закону ω
= -8t.
Определить угол φ поворота тела в момент
времени t
= 3 с,
если при t0
= 0
угол поворота φ0
= 5 рад.
(Ответ:
φ
=
-31
рад.).
Задача
№ 8.7.
Тело
вращается вокруг неподвижной оси
согласно закону
φ
= t3
+ 2.
Определить
угловую скорость ω
тела в момент времени, когда угол поворота
φ
= 10 рад.
(Ответ:
ω
=
12
с-1).
Задача
№ 8.8.
Частота
вращения маховика за время t1
=
10 с
уменьшилась в 3
раза
и стала равной 30
об/мин.
Определить угловое ускорение ε
вала, если он вращался равнозамедленно.
(Ответ:
ε
=
– 0,628 с-2).
Задача
№ 8.9.
Угловое
ускорение тела изменяется согласно
закону ε
= 2t.
Определить угловую скорость ω
тела в момент времени t
= 4 с,
если
при t0
= 0
угловая скорость равна нулю. (Ответ:
ω
=
16 с-1).
Задача
№ 8.10.
Тело
вращается вокруг неподвижной оси
согласно закону
φ
= 2t2.
Определить нормальное ускорение
точки
тела на расстоянии r
= 0,2 м
от оси вращения в момент времени t=
2 с.
(Ответ:
=
12,8
м/с2).
Вопросы для
самопроверки
1.
Сформулируйте теорему, определяющую
свойства поступательного движения.
2.
Что называют
вращательным движением твёрдого тела
вокруг неподвижной оси?
3.
Ось вращения, угол поворота и закон
вращательного движения твёрдого тела.
4.
Угловая
скорость и
угловое
ускорение при вращательном движении
твёрдого тела.
5.
Равномерное и равнопеременное вращение.
Угловое перемещение.
6.
Чему равна
линейная скорость точки вращающегося
тела?
7.
Скорости и
ускорения точек вращающегося тела.
Окружная скорость.
8.
Нормальное, тангенциальное и полное
ускорения точки вращающегося тела.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #