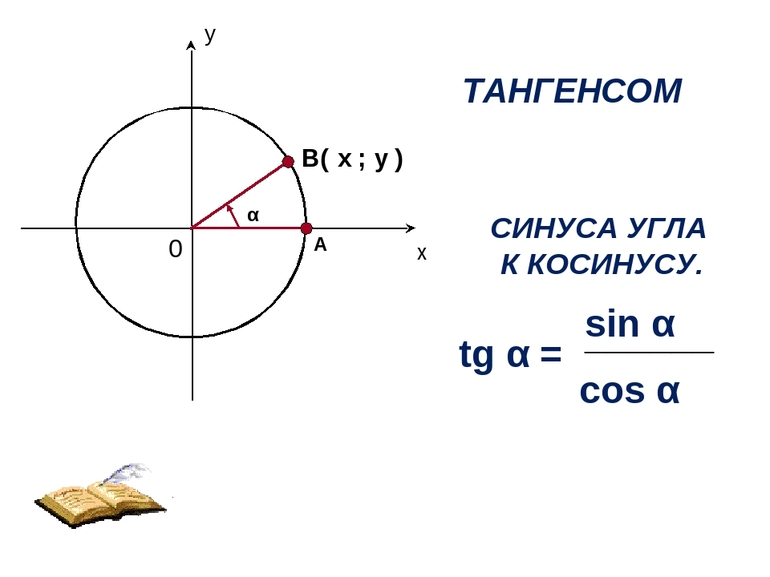
Четырехугольники, вписанные в окружность. Теорема Птолемея
Вписанные четырёхугольники и их свойства
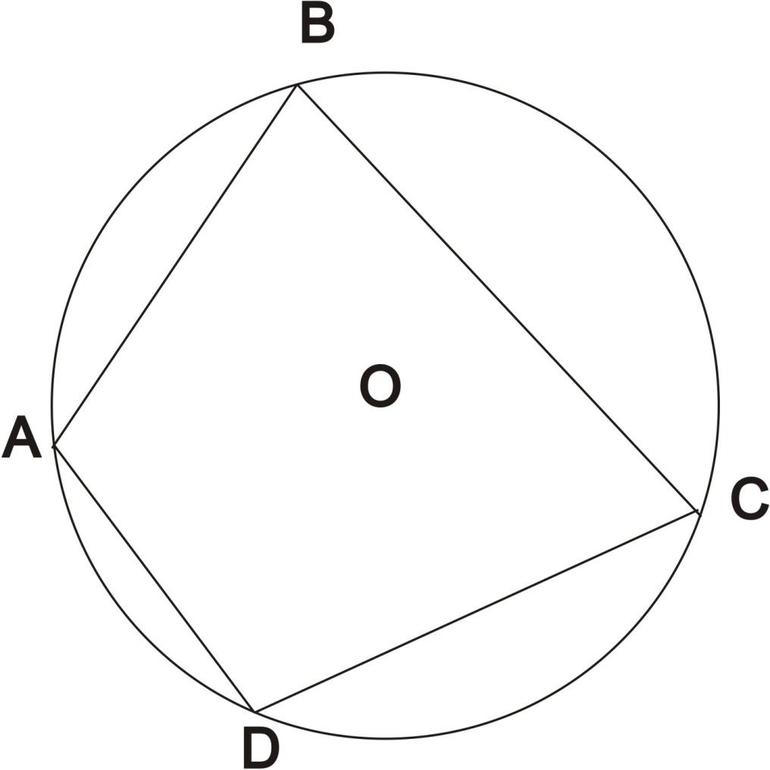
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .
Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .
Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
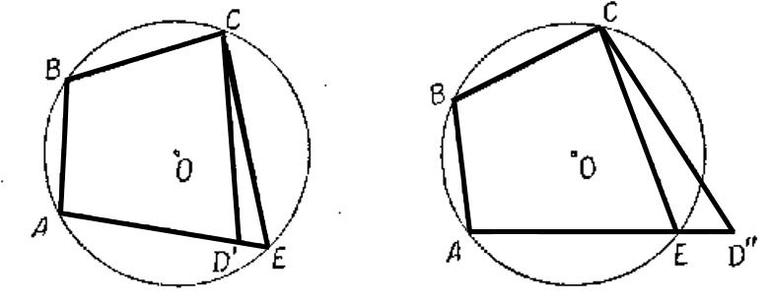
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
| Фигура | Рисунок | Свойство |
| Окружность, описанная около параллелограмма |  |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба |  |
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции |  |
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |  |
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник |  |
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
| Окружность, описанная около параллелограмма | |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба | |
 |
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции | |
 |
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида | |
 |
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник | |
 |
| Окружность, описанная около параллелограмма |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:


где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
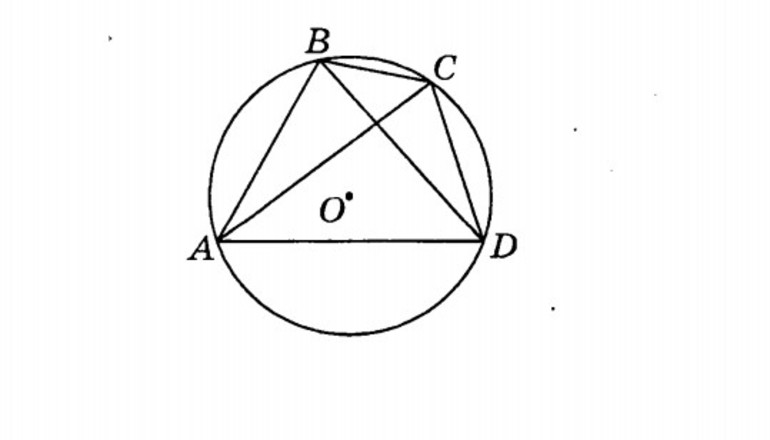
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:
 |
(1) |
Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
- Треугольник
- Выпуклый, правильный многоугольник
- Квадрат
- Равнобедренная трапеция
- Ромб
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
- В любой треугольник может быть вписана окружность, причем только один раз.
- Центр вписанной окружности — точка пересечения биссектрис треугольника.
- Вписанная окружность касается всех сторон треугольника.
- Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac<1><2>(a+b+c) cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
окружность и любая из сторон треугольника.
перпендикуляры к любой точке касания.
треугольника на 3 пары равных отрезков.
Поэтому, расстояние между центрами этих окружностей можно найти с помощью формулы Эйлера:
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
- Не во всякий четырехугольник можно вписать окружность.
- Если у четырехугольника суммы длин его противолежащих
сторон равны, то окружность, может быть, вписана (Теорема Пито). - Центр вписанной окружности и середины двух
диагоналей лежат на одной прямой (Теорема Ньютона, прямая Ньютона). - Точка пересечения биссектрис — это центр вписанной окружности.
- Точка касания — это точка, в которой соприкасается
окружность и любая из сторон четырехугольника. - Площадь четырехугольника, в который вписана окружность, можно рассчитать по такой формуле:
[ S = frac<1><2>(a+b+c+d)cdot r = pr ]
p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.
равноудалены от этой конца и начала этой стороны, то есть от его вершин.
Примеры вписанной окружности
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
- Радиус вписанной окружности в треугольник и радиус вписанной
в четырехугольник вычисляется по одной и той же формуле. Верное утверждение. - Любой параллелограмм можно вписать в окружность. Неверное утверждение.
- В любой четырехугольник можно вписать окружность. Неверное утверждение.
- В любой ромб можно вписать окружность. Верное утверждение.
- Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
- Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
- Угол вписанный в окружность равен соответствующему центральному
углу опирающемуся на ту же дугу. Неверное утверждение. - Радиус вписанной окружности в прямоугольный треугольник равен
половине разности суммы катетов и гипотенузы. Верное утверждение. - Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
- Вписанная окружность в треугольник имеет в общем
три общие точки со всеми сторонами треугольника. Верное утверждение.
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Вписанная в четырехугольник окружность
Описанный четырехугольник — это четырехугольник, все стороны которого касаются окружности. При этом окружность называется вписанной в четырехугольник.
Какими свойствами обладает вписанная в четырехугольник окружность? Когда в четырехугольник можно вписать окружность? Где находится центр вписанной окружности?
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противолежащих сторон равны.
В четырехугольник ABCD можно вписать окружность, если
И обратно, если суммы противоположных сторон четырехугольника равны:
то в четырехугольник ABCD можно вписать окружность.
Центр вписанной в четырехугольник окружности — точка пересечения его биссектрис.
O — точка пересечения биссектрис четырехугольника ABCD.
AO, BO, CO, DO — биссектрисы углов четырехугольника ABCD,
то есть ∠BAO=∠DAO, ∠ABO=∠CBO и т.д.
3. Точки касания вписанной окружности, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины.
AM=AN,
5. Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
где p — полупериметр четырехугольника.
Так как суммы противолежащих сторон описанного четырехугольника равны, полупериметр равен любой из пар сумм противолежащих сторон.
Например, для четырехугольника ABCD p=AD+BC или p=AB+CD и
Соответственно, радиус вписанной в четырехугольник окружности равен
[spoiler title=”источники:”]
http://colibrus.ru/vpisannaya-okruzhnost/
[/spoiler]
Задача
Четырехугольник ABCD со сторонами AB=40 и CD=10 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60º. Найти радиус окружности, описанной около этого четырёхугольника.
 Дано: ABCD — четырёхугольник, вписанный в окружность (O;R), AB=40, CD=10, AC∩BD=K, ∠AKB=60º
Дано: ABCD — четырёхугольник, вписанный в окружность (O;R), AB=40, CD=10, AC∩BD=K, ∠AKB=60º
Найти: R
Решение:
Радиус описанной около четырёхугольника окружности можно найти как радиус окружности, описанной около любого из треугольников, образованной вершинами четырёхугольника, например, около треугольника ABC. Если использовать формулу
![]()
для стороны AB, то искомый радиус
![]()
Длина AB известна. Значит, задача сводится к нахождению синуса угла ACB.
 Рассмотрим треугольники ABK и DCK.
Рассмотрим треугольники ABK и DCK.
1)∠ABK=∠DCK (как вписанные углы, опирающиеся на одну дугу AD);
2)∠AKB=∠DKC (как вертикальные).
Следовательно, треугольники ABK и DCK подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
![]()
Пусть CK=x, тогда BK=4x.
Рассмотрим треугольник BCK.
∠BKC+∠AKB=180º (как смежные), отсюда ∠BKC=180º-∠AKB=120º. По теореме косинусов
![]()
cos∠BKC=cos120º=-1/2,
![]()
![]()
По теореме синусов
![]()
![]()
sin∠BKC=sin120º=√3/2,
![]()
Следовательно,
![]()
Ответ: 10√7.

Примеры вписанных четырёхугольников.
Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.
Все треугольники имеют описанные окружности, но не все четырёхугольники.
Примером четырёхугольника, который нельзя вписать в окружность, может служить ромб (если только он не является квадратом). Секция «Свойства» ниже даёт необходимые и достаточные условия, чтобы вокруг четырёхугольника можно было описать окружность.
Специальные случаи[править | править код]
Любые квадраты, прямоугольники, равнобедренные трапеции или антипараллелограммы можно вписать в окружность. Дельтоид можно вписать в том и только в том случае, когда у него два угла прямые. Бицентричный четырёхугольник[en] — это вписанный четырёхугольник, который также является и описанным, а внешне бицентричный четырёхугольник — это вписанный четырёхугольник, который является также
внешне описанным[en].
Свойства[править | править код]
- Первый критерий вписанности четырёхугольника. Выпуклый невырожденный четырёхугольник является вписанным тогда и только тогда, когда четыре серединных перпендикуляра, проведённых к каждой из сторон, пересекаются в одной точке[1].
- Второй критерий вписанности четырёхугольника. Выпуклый четырёхугольник
является вписанным тогда и только тогда, когда противоположные углы в сумме дают 180°, то есть[2].
- Другой вариант первого критерия вписанности четырёхугольника. Теорема была Предложением 22 в книге 3 Евклида Начала[3]. Эквивалентно, выпуклый четырёхугольник является вписанным тогда и только тогда, когда смежный угол равен противоположному внутреннему углу.
- Третий критерий вписанности четырёхугольника. Около четырёхугольника можно описать окружность тогда и только тогда, когда любая пара его противоположных сторон антипараллельна.
- Четвертый критерий вписанности четырёхугольника. Другой критерий для того, чтобы выпуклый четырёхугольник
был вписанным, требует, чтобы угол между стороной и диагональю был равен углу между противоположной стороной и другой диагональю[4]. Например,
- Пятый критерий вписанности четырёхугольника. Неравенство Птолемея утверждает, что произведение длин двух диагоналей p и q четырёхугольника равно сумме произведений противоположных сторон, только если четырёхугольник вписан: [5]
.
- Шестой критерий вписанности четырёхугольника. Около четырёхугольника можно описать окружность тогда и только тогда, когда любая пара его противоположных сторон антипараллельна.Если две прямые, из которых одна содержит отрезок AC, а другая — отрезок BD, пересекаются в точке E, то четыре точки A, B, C, D лежат на окружности тогда и только тогда, когда[6]
Точка пересечения E может лежать как внутри, так и вне окружности. В первом случае это будет вписанный четырёхугольник ABCD, а во втором — вписанный четырёхугольник ABDC. Если пересечение лежит внутри, равенство означает, что произведение отрезков, на которые точка E делит одну диагональ, равно произведению отрезков другой диагонали. Это утверждение известно как теорема о пересекающихся хордах, поскольку диагонали вписанного четырёхугольника являются хордами описанной окружности.
- Седьмой критерий вписанности четырёхугольника. Выпуклый четырёхугольник ABCD является вписанным тогда и только тогда, когда [7]


ABCD – циклический четырехугольник, в котором E – точка пересечения диагоналей, F – точка пересечения продолжений сторон AD и BC, G – точка пересечения продолжений сторон AB и CD.(см. рис.) 

.

ABCD является циклическим четырехугольником. E – точка пересечения диагоналей, F – точка пересечения продолжений сторон BC и AD. 

(1) 




(2) 




- Замечание. Седьмой и восьмой критерии вписанности четырёхугольника очень похожи и рисунки у них очень похожи. Возможно, что это – один и тот же критерий вписанности четырёхугольника, взятый из разных первоисточников. На обоих рисунках
и
– точки Паскаля. Есть и другие сходные точки. Хотя формально звучат оба критерия по-разному.
- Десятый критерий вписанности четырёхугольника. Условие, при котором совмещение двух треугольников с одной равной стороной даёт четырёхугольник, вписанный в окружность[12]. Для того, чтобы два треугольника с тройками длин сторон соответственно (a, b, f) и (c, d, f) при их совмещении вдоль общей стороны с длиной, равной f, давали в итоге четырёхугольник, вписанный в окружность с последовательностью сторон (a, b, c, d), необходимо условие[13]:84
- Замечание. Последнее условие даёт выражение для диагонали f четырёхугольника, вписанного в окружность, через длины четырёх его сторон (a, b, c, d). Эта формула немедленно следует при перемножении и при приравнивании друг другу левых и правых частей формул, выражающих суть первой и второй теорем Птолемея.

Теорема Микеля-Штейнера для четырёхстронника
- Одиннадцатый критерий вписанности четырёхугольника. Выпуклый четырёхугольник (см. рис. справа), образованный четырьмя данными прямыми Микеля, вписан в окружность тогда и только тогда, когда точка Микеля M четырёхугольника лежит на прямой, соединяющей две из шести точек пересечения прямых (те, которые не являются вершинами четырёхугольника). То есть, когда M лежит на EF (см. рис. справа).
Площадь[править | править код]
Площадь S вписанного четырёхугольника со сторонами a, b, c, d задаётся формулой Брахмагупты[14]
где p, полупериметр, равен 
Вписанный четырёхугольник имеет максимальную площадь среди всех четырёхугольников, имеющих ту же последовательность длин сторон. Это другое следствие соотношения Бретшнайдера. Утверждение можно доказать с помощью математического анализа[15].
Четыре неравные длины, каждая из которых меньше суммы остальных трёх, являются сторонами трёх неконгруэнтных вписанных четырёхугольников[16], и по формуле Брахмагупты все эти треугольники имеют одинаковую площадь. В частности, для сторон a, b, c и d сторона a может быть противоположной любой из сторон b, c или d. Любые два из этих трёх вписанных четырёхугольников имеют диагональ одинаковой длины[17].
Площадь вписанного четырёхугольника с последовательными сторонами a, b, c, d и углом B между сторонами a и b можно выразить формулой[5]
или[18]
где θ — любой угол между диагоналями. Если угол A не является прямым, площадь можно выразить формулой [18]
Ещё одна формула площади [19]
где R — радиус описанной окружности. Прямым следствием будет [20]
,
и неравенство превращается в равенство в том и только в том случае, когда четырёхугольник является квадратом.
Диагонали[править | править код]
Во вписанном четырёхугольнике с вершинами A, B, C, D (в указанной последовательности) и сторонами a = AB, b = BC, c = CD и d = DA длины диагоналей p = AC и q = BD можно выразить через стороны [21][22][17]
и
что даёт равенство Птолемея
Согласно второй теореме Птолемея[21][22],
при тех же обозначениях, что и прежде.
Для суммы диагоналей имеем неравенство [23]
Неравенство становится равенством в том и только в том случае, когда диагонали имеют одинаковую длину, что можно показать, используя неравенство между средним арифметическим и средним геометрическим.
Более того[24],
В любом выпуклом четырёхугольнике две диагонали делят четырёхугольник на четыре треугольника. Во вписанном четырёхугольнике противоположные пары этих четырёх треугольников подобны.
Если M и N являются средними точками диагоналей AC и BD, то[25]
где E и F — точки пересечения противоположных сторон.
Если ABCD — вписанный четырёхугольник и AC пересекает BD в точке P, то [26]
Формулы углов[править | править код]
Для вписанного четырёхугольника со сторонами a, b, c, d, полупериметром p и углом A между сторонами a и d тригонометрические функции угла A равны[27]
Для угла θ между диагоналями выполняется[18]
Если продолжения противоположных сторон a и c пересекаются под углом 
где p — полупериметр[28]
Формула Парамешвары[править | править код]
Для вписанного четырёхугольника со сторонами 




Формула была выведена индийским математиком Ватассери Парамешварой[en] в 15 веке.
Используя формулу Брахмагупты, формулу Парамешвары можно преобразовать в
,
где 
Антицентр и коллинеарность[править | править код]
Четыре отрезка прямых, перпендикулярных одной стороне вписанного четырёхугольника и проходящих через середину противоположной стороны, пересекаются в одной точке[30][31]. Эта точка пересечения называется антицентром. Антицентр симметричен центру описанной окружности относительно “вершинного центроида”. Таким образом, во вписанном четырёхугольнике центр описанной окружности, “вершинный центроид” и антицентр лежат на одной прямой[31].
Если диагонали вписанного четырёхугольника пересекаются в точке P, а середины диагоналей — V и W, то антицентр четырёхугольника является ортоцентром треугольника VWP, а вершинный центроид находится в середине отрезка, соединяющего середины диагоналей [31].
Во вписанном четырёхугольнике “центроид площади” Ga, “центроид вершин” Gv и пересечение P диагоналей лежат на одной прямой. Для расстояний между этими точками выполняется равенство[32]
Другие свойства[править | править код]

- Теорема Монжа об ортоцентре вписанного четырехугольника. 4 отрезка прямых (4 антимедатрисы), проведенных из середин 4 сторон вписанного четырехугольника перпендикулярно к противолежащим сторонам, пересекаются в ортоцентре Н этого четырехугольника.[33],[34]
- Японская теорема о вписанном четырёхугольнике. Во вписанном четырёхугольнике ABCD центры вписанных окружностей треугольников ABC, BCD, CDA и DAB являются вершинами прямоугольника. Это одна из теорем, известных как японская теорема. Ортоцентры тех же четырёх треугольников являются вершинами четырёхугольника, равного ABCD. Центроиды этих четырёх треугольников являются вершинами другого вписанного четырёхугольника[4].
- Следствие теоремы о вписанном угле. Во вписанном четырёхугольнике ABCD с центром описанной окружности O пусть P — точка пересечения диагоналей AC и BD. Тогда угол APB является средним арифметическим углов AOB и COD. Это является прямым следствием теоремы о вписанном угле и теоремы о внешнем угле треугольника[en].
- Теорема о перпендикулярности внутренних биссектрис углов при вершинах E и F, образованных на пересечениях двух пар противоположных сторон вписанного четырёхугольника. Если противоположные стороны вписанного четырёхугольника продолжить до пересечения в точках E и F, то внутренние биссектрисы углов в E и F перпендикулярны[16].
- Теорема о числовом четырехугольнике. Не существует вписанных четырёхугольников с рациональной площадью и неравными рациональными сторонами, образующими арифметическую, либо геометрическую прогрессию[36].
- Теорема о числовом четырехугольнике. Если вписанный четырёхугольник имеет длины сторон, образующие арифметическую прогрессию, то четырёхугольник является также внешне описанным[en].
Четырёхугольники Брахмагупты[править | править код]
Четырёхугольник Брахмагупты[37] — это вписанный четырёхугольник с целочисленными длинами сторон, целочисленными длинами диагоналей и целочисленной площадью.
Все четырёхугольники Брахмагупты со сторонами a, b, c, d, диагоналями e, f, площадью S, и радиусом описанной окружности R можно получить путём избавления от знаменателя в следующих выражениях (при рациональных параметрах t, u и v):
Свойства ортодиагональных вписанных четырёхугольников[править | править код]
Площадь и радиус описанной окружности[править | править код]
Пусть для вписанного четырёхугольника, являющегося также ортодиагональным (т.е. имеющим перпендикулярные диагонали), пересечение диагоналей делит одну диагональ на отрезки длиной p1 и p2, а другую делит на отрезки длиной q1 и q2. Тогда[38] (первое равенство является Предложением 11 в книге Архимеда «Леммы»)
,
где D — диаметр описанной окружности. Равенство выполняется ввиду того, что диагонали являются перпендикулярными хордами окружности. Отсюда следует, что радиус описанной окружности R удовлетворяет равенству
или, через стороны четырёхугольника
Отсюда также следует, что
Таким образом, согласно формуле Эйлера, радиус можно выразить через диагонали p и q и расстояние x между серединами диагоналей
Формула для площади K вписанного ортодиагонального четырёхугольника можно получить непосредственно через стороны, если скомбинировать теорему Птолемея (см. выше) и формулу площади ортодиагонального четырёхугольника. В результате получим
Другие свойства[править | править код]
- Во вписанном ортодиагональном четырёхугольнике антицентр совпадает с точкой пересечения диагоналей[39].
- Теорема Брахмагупты утверждает, что во вписанном четырёхугольнике, являющемся также ортодиагональным, перпендикуляр от любой стороны через точку пересечения диагоналей делит противоположную сторону пополам[39].
- Если вписанный четырёхугольник является также ортодиагональным, расстояние от центра описанной окружности до любой стороны равно половине длины противоположной стороны [39].
- Во вписанном ортодиагональном четырёхугольнике расстояние между серединами диагоналей равно расстоянию между центром описанной окружности и точкой пересечения диагоналей [39].
См. также[править | править код]
- Теорема о бабочке
- Описанная окружность
- Степень точки относительно окружности
- Таблица хорд Птолемея[en]
- Пятиугольник Роббинса
- Внеописанный четырёхугольник
- Четырёхугольник
Примечания[править | править код]
- ↑ Usiskin, 2008, с. 63–65, Глава 10. Cyclic quadrilaterals.
- ↑ Usiskin, 2008, с. 63–65.
- ↑ Joyce, 1997, с. Book 3, Proposition 22.
- ↑ 1 2 Andreescu, Enescu, 2004, с. 2.3 Cyclic quads.
- ↑ 1 2 Durell, Robson, 2003, с. 25.
- ↑ Bradley, 2007, с. 179.
- ↑ Hajja, 2008, с. 103–6.
- ↑ Fraivert, David. New points that belong to the nine-point circle (англ.) // The Mathematical Gazette (англ.) (рус. : journal. — 2019. — July (vol. 103, no. 557). — P. 222—232. — doi:10.1017/mag.2019.53.
- ↑ Fraivert, David. New applications of method of complex numbers in the geometry of cyclic quadrilaterals (англ.) // International Journal of Geometry : journal. — 2018. — Vol. 7, no. 1. — P. 5—16. Архивировано 7 июня 2019 года.
- ↑ 1 2 3 Fraivert, David; Sigler, Avi & Stupel, Moshe (2020), Necessary and sufficient properties for a cyclic quadrilateral, International Journal of Mathematical Education in Science and Technology, <https://doi.org/10.1080/0020739X.2019.1683772> Архивная копия от 10 июня 2020 на Wayback Machine
- ↑ 1 2 Фрейверт, Д. М. (2019), Новая тема в евклидовой геометрии на плоскости: теория «точек Паскаля», формируемых с помощью окружности на сторонах четырехугольника, Математическое образование: современное состояние и перспективы : материалы Международной научной конференции, <http://libr.msu.by/handle/123456789/9675> Архивная копия от 10 ноября 2019 на Wayback Machine
- ↑ См. подраздел «Диагонали» статьи «Вписанный четырёхугольник»
- ↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ. Co., 2007
- ↑ Durell, Robson, 2003, с. 24.
- ↑ Peter, 2003, с. 315–6.
- ↑ 1 2 Coxeter, Greitzer, 1967, с. 57, 60.
- ↑ 1 2 Johnson, 2007, с. 84.
- ↑ 1 2 3 Durell, Robson, 2003, с. 26.
- ↑ Prasolov, 2006, с. 86, Задача 4.44.
- ↑ Alsina, Nelsen, 2009, с. 64.
- ↑ 1 2 Durell, Robson, 2003, с. 25,.
- ↑ 1 2 3 Alsina, Nelsen, 2007, с. 147–9.
- ↑ Crux, 2007, с. 123, # 2975.
- ↑ Crux, 2007, с. 64, #1639.
- ↑ ABCD is a Cyclic quadrilateral. Let M, N be midpoints of diagonals AC, BD respectively… (недоступная ссылка — история). Art of Problem Solving (2010).
- ↑ A. Bogomolny, An Identity in (Cyclic) Quadrilaterals, Interactive Mathematics Miscellany and Puzzles,
[1] Архивная копия от 28 мая 2019 на Wayback Machine, Accessed 18 March 2014. - ↑ Siddons, Hughes, 1929, с. 202.
- ↑ Durell, Robson, 2003, с. 31.
- ↑ Hoehn, 2000, с. 69–70.
- ↑ Altshiller-Court, 2007, с. 131.
- ↑ 1 2 3 Honsberger, 1995, с. 35–39, 4.2 Cyclic quadrilaterals.
- ↑ Bradley, 2011.
- ↑ Замечательные точки и линии четырехугольников// https://math.mosolymp.ru/upload/files/2018/khamovniki/geom-10/2018-04-17-Zam_pr_ch-ka.pdf Архивная копия от 6 сентября 2022 на Wayback Machine
- ↑ Теорема Монжа// https://bambookes.ru/stuff/reshenie_zadach/geometrija/4-1-0-8264 Архивная копия от 6 сентября 2022 на Wayback Machine
- ↑ Вокруг задачи Архимеда. Архивная копия от 29 апреля 2016 на Wayback Machine Упр. 7, рис. 11, следствие, c. 5
- ↑ Buchholz, MacDougall, 1999, с. 263–9.
- ↑ Sastry, 2002, с. 167–173.
- ↑ Posamentier, Salkind, 1970, с. 104–5.
- ↑ 1 2 3 4 Altshiller-Court, 2007, с. 131,137-8.
Литература[править | править код]
- Claudi Alsina, Roger Nelsen. When Less is More: Visualizing Basic Inequalities, Сhapter 4.3 Cyclic, tangential, and bicentric quadrilaterals. — Mathematical Association of America, 2009. — ISBN 978-0-88385-342-9.
- Claudi Alsina, Roger B. Nelsen. On the diagonals of a cyclic quadrilateral // Forum Geometricorum. — 2007. — Т. 7.
- Nathan Altshiller-Court. College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. — 2nd. — Courier Dover, 2007. — ISBN 978-0-486-45805-2. (org. 1952)
- =Titu Andreescu, Bogdan Enescu. Mathematical Olympiad Treasures. — Springer, 2004. — ISBN 978-0-8176-4305-8.
- Christopher Bradley. Three Centroids created by a Cyclic Quadrilateral. — 2011.
- Christopher J. Bradley. The Algebra of Geometry: Cartesian, Areal and Projective Co-Ordinates. — Highperception, 2007. — ISBN 1906338000.
- R. H. Buchholz, J. A. MacDougall. Heron quadrilaterals with sides in arithmetic or geometric progression // Bulletin of the Australian Mathematical Society. — 1999. — Т. 59, вып. 2. — doi:10.1017/S0004972700032883.
- Harold Scott MacDonald Coxeter, Samuel L. Greitzer. Geometry Revisited. 3.2 Cyclic Quadrangles; Brahmagupta’s formula. — Mathematical Association of America, 1967. — ISBN 978-0-88385-619-2. Перевод Г. С. М. Коксетер, С. Л. Грейтцер. Новые встречи с геометрией. 3.2 Вписанные четырёхугольники; Теорема Брахмагупты. — Москва: «Наука», 1978. — (Библиотека математического кружка).
- Crux Mathematicorum. Inequalities proposed in Crux Mathematicorum. — 2007.
- D. Fraivert. The theory of an inscribable quadrilateral and a circle that forms Pascal points // Journal of Mathematical Sciences: Advances and Applications. — 2016. — Т. 42. — P. 81–107. — doi:10.18642/jmsaa_7100121742.
- C. V. Durell, A. Robson. Advanced Trigonometry. — Courier Dover, 2003. — ISBN 978-0-486-43229-8. (orig. 1930)
- Mowaffaq Hajja. A condition for a circumscriptible quadrilateral to be cyclic // Forum Geometricorum. — 2008. — Т. 8.
- Larry Hoehn. Circumradius of a cyclic quadrilateral // Mathematical Gazette. — 2000. — Т. 84, вып. 499 March. — JSTOR 3621477.
- Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. — Cambridge University Press, 1995. — Т. 37. — (New Mathematical Library). — ISBN 978-0-88385-639-0.
- Roger A. Johnson. Advanced Euclidean Geometry. — Dover Publ, 2007. (orig. 1929)
- Thomas Peter. Maximizing the area of a quadrilateral // The College Mathematics Journal. — 2003. — Т. 34, вып. 4 September. — JSTOR 3595770.
- Alfred S. Posamentier, Charles T. Salkind. Challenging Problems in Geometry. — 2nd. — Courier Dover, 1970. — ISBN 978-0-486-69154-1. Глава: Solutions: 4-23 Prove that the sum of the squares of the measures of the segments made by two perpendicular chords is equal to the square of the measure of the diameter of the given circle.
- , <http://students.imsa.edu/~tliu/Math/planegeo.pdf> Архивная копия от 21 сентября 2018 на Wayback Machine Перевод с русского издания В.В. Прасолов. Задачи по планиметрии. Учебное пособие. — 5-е. — Москва: МЦНМО OAO «Московские учебники», 2006. — ISBN 5-94057-214-6.
- K.R.S. Sastry. Brahmagupta quadrilaterals // Forum Geometricorum. — 2002. — Т. 2.
- A. W. Siddons , R. T. Hughes. Trigonometry. — Cambridge University Press, 1929.
- Zalman Usiskin, Jennifer Griffin, David Witonsky, Edwin Willmore. The Classification of Quadrilaterals: A Study of Definition. — IAP, 2008. — (Research in mathematics education). — ISBN 978-1-59311-695-8.
- D. E. Joyce. Euclid’s Elements. — Clark University, 1997.
- D. Fraivert. Pascal-points quadrilaterals inscribed in a cyclic quadrilateral // The Mathematical Gazette. — 2019. — Т. 103, вып. 557.
Внешние ссылки[править | править код]
- Derivation of Formula for the Area of Cyclic Quadrilateral
- Incenters in Cyclic Quadrilateral at cut-the-knot
- Four Concurrent Lines in a Cyclic Quadrilateral at cut-the-knot
- Weisstein, Eric W. Cyclic quadrilateral (англ.) на сайте Wolfram MathWorld.
- Euler centre and maltitudes of cyclic quadrilateral at Dynamic Geometry Sketches, interactive dynamic geometry sketch.
Свойства вписанных и описанных четыехугольников
Содержание:
- Вписанный четырехугольник, особенности, основные свойства фигуры
- Описанный четырехугольник, особенности, основные свойства фигуры
- Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
- Чему равна сумма противоположных углов вписанного в окружность четырехугольника
- Как найти радиус вписанного в окружность четырехугольника, формула
Вписанный четырехугольник, особенности, основные свойства фигуры
Вписанный в окружность четырехугольник является таким четырехугольником, каждая из вершин которого принадлежит описанной около него окружности.
Вписанный в окружность четырехугольник изображен на рисунке:
Здесь около четырехугольника ABCD описана окружность, а сам этот четырехугольник можно назвать вписанным в данную окружность. Этот вывод можно сделать на основании определения, рассмотренного ранее, так как точки A, B, C, D являются одновременно и вершинами четырехугольника, и принадлежат описанной около него окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Теорема 1
Какой-либо четырехугольник может быть вписан в некую окружность при условии, что его противолежащие углы в сумме дают 180°.
Теорема 2
В том случае, когда противолежащие углы некого четырехугольника в сумме составляют 180°, данный четырехугольник может быть вписан в окружность.
На примере рисунка запишем смысл изложенной теоремы:
(left. begin{array}{l} angle A + angle C = {180^o}\ angle B + angle D = {180^o} end{array} right} Leftrightarrow ABCD) треугольник вписан в окружность.
Следствие 1
Не каждый параллелограмм допустимо вписывать в окружность, лишь прямоугольники — в том числе квадраты.
Если какой-то четырехугольник вписан в окружность, то ее центральная точка совпадет с точкой, в которой пересекаются диагонали вписанного четырехугольника. При этом радиус описанной около четырехугольника окружности составит половину от длины его диагонали, то есть:
(R = frac{1}{2}BD)
Радиус, окружности, описанной около некого четырехугольника с прямыми углами, можно вычислить с помощью следующей формулы, содержащей стороны прямоугольника:
(R = frac{1}{2}sqrt {A{B^2} + A{D^2}}.)
Представим, что прямоугольник имеет стороны, которые равны a и b. Тогда справедливо следующее соотношение:
(R = frac{1}{2}sqrt {{a^2} + {b^2}})
Следствие 2
Допустимо вписать в окружность лишь такую трапецию, которая является равнобедренной.
Выведем формулу для вычисления радиуса окружности, которая описана около равнобедренной трапеции. Искомая величина равна радиусу окружности, описанной около одного из треугольников, имеющего те же вершины, что и рассматриваемая трапеция:
ABC, ABD, ACD или BCD.
Описанный четырехугольник, особенности, основные свойства фигуры
Описанным четырехугольником называют такую геометрическую фигуру с четырьмя углами, каждая из сторон которой является касательной к окружности. Данная окружность считается вписанной в рассматриваемый четырехугольник.
Теорема 3
В любой четырехугольник допустимо вписать какую-либо окружность при условии, что его противолежащие стороны в сумме равны.
Заметим, что в данном случае соблюдено условие:
AB+CD=BC+AD
На основе теоремы можно сформулировать обратное утверждение. В том случае, когда противоположные стороны четырехугольника в сумме равны, то есть AB+CD=BC+AD, в такой четырехугольник ABCD допустимо вписать какую-либо окружность.
Теорема 4
Центральная точка окружности, вписанной в четырехугольник, совпадает с точкой, в которой пересекаются биссектрисы данной геометрической фигуры.
Заметим, что на рисунке биссектрисами углов, которые имеет четырехугольник ABCD, являются следующие отрезки:
- AO;
- BO;
- CO;
- DO.
В результате:
(angle BAO = angle DAO)
(angle ABO = angle CBO) и так далее.
Теорема 5
Точки, в которых вписанная окружность касается описанного четырехугольника, расположены на сторонах с началом, совпадающим с одной вершиной, и находятся на одинаковом удалении от данной вершины.
Рассмотрим рисунок. Заметим, что:
BM=BK;
CK=CF;
DF=DN.
Записанные равенства вытекают из того факта, что это отрезки касательных, которые проведены из одной точки.
Запишем следующие соотношения:
(OM bot AB);
(OK bot BC);
(OF bot CD);
(ON bot AD).
Данные соотношения верны, так как включают в себя радиусы, которые проведены в точки касания окружности и описанного четырехугольника.
Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
В том случае, когда в четырехугольник вписана окружность, его площадь определяется по формуле:
(S = p cdot r)
Здесь p обозначает полупериметр четырехугольника.
Вспомним, что противолежащие стороны четырехугольника, в который вписана окружность, в сумме равны. Исходя из данного утверждения, можно сделать вывод: полупериметр такого четырехугольника равен какой-либо из пар сумм противолежащих сторон.
Если рассмотреть некий четырехугольник ABCD, то можно записать формулу для вычисления полупериметра этой геометрической фигуры:
p=AD+BC
p=AB+CD.
Тогда площадь четырехугольника, в который вписана окружность, будет вычислена таким образом:
({S_{ABCD}} = (AD + BC) cdot r;)
({S_{ABCD}} = (AB + CD) cdot r.)
В результате для определения радиуса окружности, которая вписана в некий четырехугольник, можно воспользоваться следующей формулой:
(r = frac{S}{p}.)
В том случае, если рассматривается описанная около четырехугольника ABCD окружность, то формула для вычисления ее радиуса примет вид:
(r = frac{{{S_{ABCD}}}}{{AD + BC}};)
(r = frac{{{S_{ABCD}}}}{{AB + CD}}.)
Чему равна сумма противоположных углов вписанного в окружность четырехугольника
Теорема 6
Если четырехугольник вписан в некую окружность, то его противолежащие углы в сумме дают .
Заметим, что на рисунке изображен четырехугольник ABCD, вписанный в окружность (O; R). Требуется доказать, что:
(angle A+angle C=180^o;)
(angle B+angle D=180^o.)
Представим доказательства. По условию:
(angle A) — угол вписанного четырехугольника, опирается на дугу BCD;
(angle C) — угол, который опирается на дугу DAB.
Зная, что вписанный угол составляет ½ часть дуги, которая является его опорой, запишем:
(angle A = frac{1}{2} cup BCD,)
(angle C = frac{1}{2} cup DAB.)
В результате:
(angle A + angle C = frac{1}{2} cup BCD + frac{1}{2} cup DAB = frac{1}{2}( cup BCD + cup DAB) = frac{1}{2} cdot 360^o = 180^o.)
Аналогичным образом запишем, что:
(angle B + angle D = frac{1}{2}( cup CDA + cup ABC) = frac{1}{2} cdot 360^o = 180^o.)
Теорема доказана.
Теорема 7
Если имеется такой четырехугольник, в котором противолежащие углы в сумме составляют (180^o), то около него можно описать окружность.
Представим, что имеется некий четырехугольник ABCD.
Сумма его противолежащих углов равна: (angle B+angle D=180^o).
Попробуем доказать, что около рассматриваемого четырехугольника можно описать окружность.
В первую очередь построим окружность около треугольника ABC таким образом, чтобы точка D принадлежала данной окружности. Построим доказательства, двигаясь «от обратного».
Допустим, что точка D не принадлежит окружности, которая описана около треугольника ABD. В таком случае точка D должна располагаться во внутренней области, ограниченной данной окружностью, или за пределами окружности.
В том случае, когда точка D расположена во внутреннем пространстве, ограниченном окружностью, какой-то луч AD имеет точку пересечения с окружностью. Обозначим ее, как Е. Заметим, что если вокруг четырехугольника ABCE описана окружность, то его противолежащие углы в сумме составляют (180^o):
(angle B+angle E = 180^o.)
Согласно данным из условия задачи:
(angle B+angle D=180^o.)
Таким образом:
(angle D=angle E.)
С другой стороны, угол D является внешним углом треугольника DCE при его вершине D. Исходя из этого, запишем:
(angle ADC=angle DEC+angle DCE.)
В результате получается, что угол D не равен углу E. Это утверждение противоречиво. Таким образом, точка D не расположена во внутреннем пространстве, ограниченном окружностью, описанной около треугольника ABC.
Луч AD имеет точку пересечения с окружностью, обозначенную буквой Е. В таком случае, ABCE представляет собой вписанный в окружность четырехугольник, а также:
(angle B+angle E=180^o)
Согласно условию задачи:
(angle B+angle D=180^o.)
Тогда:
(angle D=angle E.)
Однако угол Е является внешним углом треугольника ECD и расположен при вершине E.
Таким образом: (angle AEC=angle EDC+angle DCE.)
В результате недопустимо равенство углов D и E. В том случае, когда точка D расположена за пределами окружности, возникает противоречие. Таким образом, остается единственно верный вариант расположения этой точки, согласно которому она принадлежит окружности, описанной около четырехугольника. Теорема доказана.
Согласно свойству и признаку четырехугольника, вписанного в окружность, необходимым и достаточным условием вписанного четырехугольника является следующая теорема.
Теорема 7
Около четырехугольника допустимо описать окружность лишь в том случае, когда его противолежащие углы в сумме составляют 180 градусов.
Как найти радиус вписанного в окружность четырехугольника, формула
Допустим, что имеется некий четырехугольник, стороны которого обозначены, как a, b, c, d, а полупериметр равен p. В таком случае описанная около данного четырехугольника окружность имеет радиус, который можно рассчитать по формуле как отношение:
(R={frac {1}{4}}{sqrt {frac {(ab+cd)(ac+bd)(ad+bc)}{(p-a)(p-b)(p-c)(p-d)}}}.)
Примечание
Формулу радиуса окружности, которая описана около четырехугольника, ввел индийский математик Ватассери Парамешвара в XV веке.
Рассмотрим еще одну закономерность, которую называют формулой Брахмагупты. С ее помощью можно определить площадь S четырехугольника, который вписан в окружность и имеет стороны, равные a, b, c, d:
(S={sqrt {(p-a)(p-b)(p-c)(p-d)}}.)
В данном случае p является полупериметром, то есть в два раза меньше, чем периметр, и определяется как:
(p={tfrac {1}{2}}(a+b+c+d).)
С помощью формулы Брахмагупты представляется возможным изменить форму записи формулы Парамешвары:
(4SR={sqrt {(ab+cd)(ac+bd)(ad+bc)}}.)
Здесь S определяется, как площадь четырехугольника, вписанного в окружность. Диаметр равен двум радиусам и проходит через центр окружности.
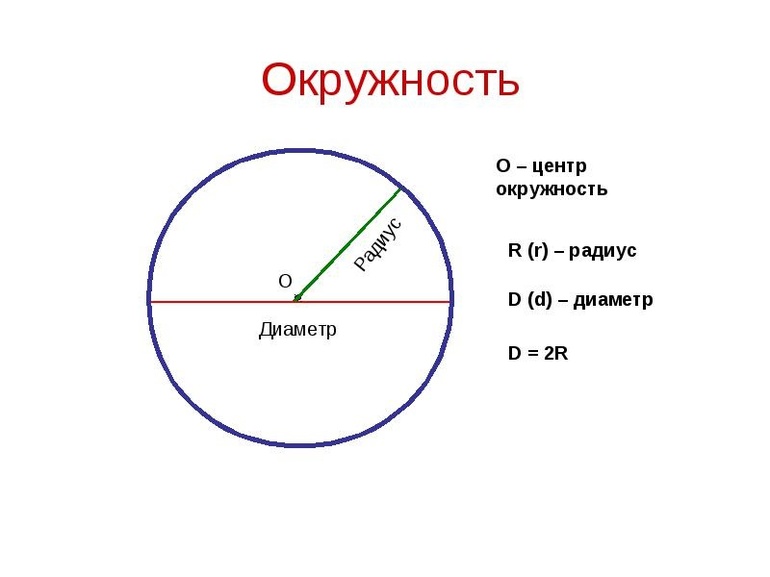
Общие сведения
Фигура является вписанной в окружность, когда все ее вершины лежат на ней. Произвести вписание в окружность четырехугольника можно только в том случае, когда он выпуклый. Все его точки находятся по одну сторону от произвольной прямой, которая проходит через соседние вершины фигуры. Нужно отметить, что в этом случае окружность является описанной вокруг фигуры. Если в параллелограмм вписана окружность, то ее центр совпадает с центром окружности, которая описана вокруг него.
Четырехугольники бывают самопересекающимися. Они также могут быть вписанными, однако это встречается крайне редко. Не каждую фигуру можно вписать в круг, поскольку существуют определенные законы. Например, вокруг ромба нельзя описать круг — исключение составляет случай, когда ромб является квадратом.
Основные правила
Выпуклый четырехугольник можно вписать в окружность. Однако для этого существуют некоторые правила (критерии) или признаки. Некоторые задачи сформулированы таким образом, что нужно знать основные критерии, а также уметь доказывать возможность вписывать или описывать окружность. Около четырехугольника можно описать окружность, если выполняются следующие условия:
- Сумма углов, которые являются противоположными, соответствует 180 градусам.
- Соблюдается равенство смежного и противоположного углов.
- Угол между стороной и диагональю равен углу между противоположной стороной и диагональю.
- Произведение двух диагоналей соответствует размерности суммы произведений противоположных сторон.
- Четыре точки лежат на окружности, когда две прямые АС и BD, образующие диагонали, пересекаются в некоторой точке P, а также выполняется следующее равенство: AP * PC = BP * PD.
- Произведения тангенсов половины двух противоположных углов равны 1. Кроме того, значения произведений эквивалентны друг другу (tg (A/2) * tg (C/2) = tg (B/2) * tg (D/2) = 1).
Четвертое утверждение является теоремой Птолемея. Все эти правила являются следствиями, полученными при доказательстве различных гипотез. Правила можно применять в зависимости от условия поставленной задачи. Любой параллелограмм можно вписать в окружность, когда он является прямоугольником или квадратом.
Свойства и утверждения
При решении можно воспользоваться некоторыми свойствами, которые были доказаны. Это нужно для того, чтобы не тратить время на выведение какой-либо формулы. Применяется методика для оптимизации вычислений. К ним можно отнести следующие:
- Если вокруг четырехугольника описана окружность, то центры окружностей, которые вписанных в треугольники, образованные диагоналями фигуры, являются вершинами прямоугольника.
- Не бывает четырехугольников, вписанных в окружность, с рациональной площадью и сторонами, которые образуют арифметический или геометрический тип прогрессии.
- При продолжении сторон до точек пересечения Y и Z, внутренние биссектрисы углов Y и Z являются перпендикулярными.
Данные утверждения применяются не всегда. В некоторых случаях можно ограничиться формулами и основными соотношениями — они позволяют легко и быстро искать нужные величины.
Формулы и соотношения
Очень часто необходимо перерыть горы информации для поиска нужной формулы. Это сказывается на оптимизации решения. Кроме того, некоторые соотношения могут содержать ошибки, поскольку материал излагается неквалифицированными специалистами.
Педагоги утверждают, что обучение какой-либо дисциплине с физико-математическим уклоном должно быть основано на алгоритмах. Кроме того, рекомендуется прочитать условие задачи несколько раз до полного его понимания. В основном необходимо находить площадь, диагонали и углы четырехугольника.
Периметр и полупериметр
Периметром выпуклого четырехугольника со сторонами a, b, c и d называется сумма длин всех его сторон. Величина обозначается литерой «Р», и вычисляется по следующей формуле: P = a + b + c +d. Кроме того, в некоторых формулах встречается величина, которая называется полупериметром. Обозначается она литерой «р». Для ее нахождения применяется такое соотношение: p = P / 2 = (a + b + c +d) / 2. Единицей измерения полупериметра являются метрические величины: мм, см, дм, м и т. д.
Для квадрата формула периметра имеет вид: P = 4 * a. Равенство легко доказывается для фигуры со стороной а. Из определения периметра получается соотношение: P = a + a + a + a. Если привести подобные слагаемые, то результирующая формула имеет вид: P = 4 * a. У прямоугольника противоположные стороны равны. Чтобы найти его периметр, нужно воспользоваться равенством: P = a + b + a + b = 2 * (a + b). Необходимо отметить, что квадрат является правильным четырехугольником, поскольку его стороны равны между собой.
Понятие площади
Площадь двумерных фигур — понятие геометрии, которое показывает ее численную характеристику или размер. Очень часто она обозначается литерой S. Измеряется величина в квадратных единицах (см 2 , м 2 и т. д. ). Фигура, имеющая характеристику S, называется квадратируемой.
Для нахождения S применяется интегральный метод, но существуют частные случаи, при которых интегрировать необязательно. Очень часто возникает необходимость перевода одной единицы в другую. Для этого существует простой алгоритм, позволяющий корректно выполнить данную операцию. Например, нужно перевести м 2 в см 2 . Необязательно заучивать единицы площади и их эквивалентность другим. Достаточно выполнить следующие действия:
- Определить базовую единицу: м и см.
- Выполнить перевод одной метрической величины в другую: 1 м = 100 см.
- Возвести обе части выражения во втором пункте в квадрат: 1 м 2 = 100 2 см 2 = 10000 см 2 .
Однако бывают и другие единицы, которые применяются для измерения размерности земельных участков: 1 ар (сокращенно а) = 1 сотке = 100 м 2 и 1 гектар (га) = 10000 м 2.

Когда известны все стороны четырехугольника (a, b, c и d), который вписан в окружность, можно найти его S. Для этого нужно знать еще одну величину. Она называется полупериметром. Расчет выполняется по формуле: S = [(p — a) * (p — b) * (p — c) * (p — d)]^(½). Соотношение называется формулой Брахмагупты.
Необходимо отметить, что вписанный четырехугольник обладает максимальным значением S среди остальных эквивалентных фигур. Если известны четыре стороны, которые являются последовательными (a, b, c и d), а также угол В между a и b, то можно воспользоваться более упрощенной формулой: S = [(a * b + c * d) * sin (B)] / 2. В случае, когда известны все стороны и любой угол (Y) между диагоналями, соотношение можно записать таким образом: S = [(a * с + и * d) * sin (Y)] / 2.
Площадь можно выразить и другим соотношением, когда известны все стороны и угол А, который не является прямым: S = [(a 2 — b 2 — c 2 + d 2 ) * tg (A)] / 4. При известном радиусе описанной окружности и углах (A, B и Y) можно воспользоваться такой формулой: S = 2 * R^(2) * sin (A) * sin (B) * sin (Y). Следствием из последнего соотношения является S <= 2 * R 2 . Если четырехугольник является квадратом, то неравенство преобразуется в равенство, т. е. S = 2 * R 2.
Диагонали и углы
Для вписанного четырехугольника ABCD существуют определенные соотношения, по которым можно найти его диагонали. Для фигуры со сторонами a = AB, b = BC, c = CD и d = DA диагонали (s = АС и t = DA) находятся таким образом: s = [((a * c + b * d) * (a * d + b * c)) / (a * b + c * d)]^(½) и t = [((a * c + b * d) * (a * b + d * c)) / (a * d + c * b)]^(½). Если умножить диагональ s на t и привести подобные слагаемые, то в результате получится формула Птолемея: s * t = a * c + b * d.
При отношении двух диагоналей получается вторая теорема Птолемея: s / t = (a * d + b * c) / (a * b + d * c). Сумма диагоналей — есть неравенство такого вида: s + t >= 2 * [a * c + b * d]^(½). Неравенство преобразуется в равенство, когда диагонали равны. Однако в этом случае можно воспользоваться следующим выражением: [s + t]^(½) >= [a * c]^(2) + [b * d]^(2).
Необходимо отметить, что в произвольном выпуклом четырехугольнике диагонали делят его на 4 треугольника, которые являются между собой подобными по парам. Кроме того, при пересечении двух диагоналей AC и BD в некоторой точке М, справедливо следующее соотношение: AM / CM = (AB * AD) / (CB * CD).
Можно находить и некоторые углы фигуры. Для этого существуют определенные соотношения. Во вписанном четырехугольнике со сторонами, которые соответствуют значениям a, b, c и d, углом A между сторонами a и d, а также полупериметром p, функции тригонометрического типа для А вычисляются таким образом:
- cos (A) = (a 2 + d 2 — b 2 — c 2 ) / (2 * (a * d + b + c)).
- sin (A) = [(p — a) * (p — b) * (p — c) * (p — d)]^(½) / (a * d + b + c).
- tg (A/2) = [((p — a) * (p — d)) / ((p — b) * (p — c))]^(½).
В некоторых случаях нужно вычислить значение тангенса для угла Y, который находится между диагоналями, по формуле: tg (Y/2) = [((p — b) * (p — d)) / ((p — a) * (p — c))]^(½).
В геометрии существует вписанный четырехугольник, стороны которого являются целыми числами. Кроме того, целочисленными являются также его диагонали и площадь. Он называется четырехугольником Брахмагупты. Однако для преобразования любого четырехугольника в данную фигуру необходимо выполнить некоторые математические операции. Пусть он имеет следующие целочисленные параметры:
- Стороны: a, b, c и d.
- Диагонали: s и t.
- Площадь: S.
- Радиус описанной окружности: R.
В некоторых случаях возникает необходимость избавиться от рациональных значений в знаменателе. При значениях дробных параметров k, l и m нужно использовать такие соотношения:
- a = [k * (l + m) + (1 — (l * m))] * [l + m — k * (1 — (l * m))].
- b = (1 — l 2 ) * (m — k) * (1 + k * m).
- c = k * (1 + l 2 ) * (1 + m 2 ).
- d = (1 + m 2 ) * (l — k) * (1 + k * l).
- s = l * (1 + k 2 ) * (1 + m 2 ).
- t = m * (1 + k 2 ) * (1 + l 2 ).
- S = l * m * [2 * k * (1 — l * m) — (l + m) * (1 — k 2 )] * [2 * k (l + m) + (1 — l * m) * (1 — k 2 )].
- 4 * R = (1 + l 2 ) * (1 + m 2 ) * (1 + k 2 ).
Существуют также соотношения для описанной вокруг четырехугольника окружности. Математики утверждают, что при комбинации двух и более геометрических фигур время поиска некоторых параметров увеличивается.
Параметры для окружности
Радиус окружности R для четырехугольника c полупериметром р и со сторонами a, b, c, d находится по формуле Парамешвары: R = (¼) * [((a * b + c * d) * (a * c + b * d) * (a * d + b * c)) / ((p — a) * (p — b) * (p — c) * (p — d))]^(½). Соотношение было выведено в XV веке математиком из Индии Ватассери Парамешварой.
При комбинации данной формулы с соотношением Брахмагупты можно получить следующее соотношение: 4 * S * R = [(a * b + c * d) * (a * c + b * d) * (a * d + b *c)]^(½). Следует отметить, что величина S является площадью вписанного четырехугольника. Для ортогонального четырехугольника с перпендикулярными диагоналями, которые делятся на отрезки s1, s2, t1 и t2, существует некоторое соотношение, позволяющее найти диаметр окружности (D): D 2 = (s1)^2 + (s2)^2 + (t1)^2 + (t2)^2 = a 2 + c 2 = b 2 + d 2.
Радиус в этом случае находится таким образом: R = D / 2 = [(s1)^2 + (s2)^2 + (t1)^2 + (t2)^2] / 2 = [a 2 + c 2 ] / 2 = [b 2 + d 2 ] / 2. Если выполнить сложение квадратов сторон, то получится такое равенство: 8 * R = a 2 + b 2 + c 2 + d 2 . По формуле Эйлера R можно также выразить через диагонали (s и t) и расстояние v между их серединами: R = [(s 2 + t 2 + 4 * v 2 ) / 8]^(½).
Таким образом, специалисты рекомендуют на начальных этапах обучения использовать уже готовые формулы для вычисления основных параметров выпуклого четырехугольника, вписанного в окружность.
























![a=[t(u+v)+(1-uv)][u+v-t(1-uv)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cd163fbbbaa9656bd5676b09a171e5cbbb85e5b)





![{displaystyle S=uv[2t(1-uv)-(u+v)(1-t^{2})][2(u+v)t+(1-uv)(1-t^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01ea51bbbcf3ed1c6507e1656e0682cdc672ddd4)






