Число беспорядков как найти

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 декабря 2021 года; проверки требуют 7 правок.

У этого термина существуют и другие значения, см. Беспорядок.

В комбинаторике беспорядком называется перестановка без неподвижных точек.

Примеры[править | править код]

Проверка работ[править | править код]

Допустим, профессор дал четырём студентам (назовём их A, B, C и D) контрольную, а затем предложил им проверить её друг у друга. Естественно, ни один студент не должен проверять свою контрольную. Сколько у профессора вариантов распределения контрольных, в которых ни одному студенту не достанется своя работа? Из всех 24 перестановок (4!) для возврата работ, нам подходят только 9 беспорядков:

   BADC, BCDA, BDAC,
   CADB, CDAB, CDBA,
   DABC, DCAB, DCBA.

В любой другой перестановке этих 4 элементов как минимум один студент получает свою контрольную на проверку.

Задача о письмах[править | править код]

Вычисление количества беспорядков является популярной задачей в олимпиадной математике, которая встречается в разных формулировках таких как задача о беспорядке, задача о письмах, задача о встречах и так далее.

Если писем случайным образом положить в различных конвертов, то какова вероятность, что какое-нибудь из писем попадёт в свой конверт?

Ответ даётся выражением

Таким образом, ответ слабо зависит от количества писем и конвертов и примерно равен константе .

Количество беспорядков[править | править код]

Количество всех беспорядков порядка n может быть вычислено с помощью принципа включения-исключения и дается выражением

которое называется субфакториалом числа n.

Количество беспорядков удовлетворяет рекурсивным соотношениям

и

где и .

Ввиду того, что , значение с ростом ведёт себя как . Более того, при его можно представить как результат округления числа .

См. также[править | править код]

• Парадокс дней рождения

Примечания[править | править код]

Ссылки[править | править код]

• Р. Стенли. Перечислительная комбинаторика. — М.: Мир, 1990. — С. 107-108.

Пусть имеется конечное упорядоченное
множество элементов {1,…, n}. Из этих
элементов могут быть образованы
перестановки a₁,…, a_n
(a_i{1,…,n}).
Число всех возможных перестановок –
n!. Среди этих n! перестановок
есть такие, что ни один элемент не стоит
на своём месте (a_ii,
i=
).
Иначе говоря, элемент номер 1 не стоит
на 1-ом месте, элемент номер 2 не стоит
на 2-м месте, и т.д., элемент номер n
не стоит на n-м месте.
Такие перестановки называются
беспорядками.

Число беспорядков из n элементов
обозначается D_n (ясно, что
D_n<n!).

Теорема. Число беспорядков из n
элементов равно:

.

# Обозначим через свойство p_i
– «i-й элемент стоит на i-м месте».
Тогда по формуле решета

.

Общее число перестановок n
элементов – n! Число
перестановок, где i-й элемент стоит
на i-м месте, равно (n-1)! (ставим
i-й
элемент на i-е
место, а оставшиеся n-1
элементы переставляем (n-1)!
способами). При этом сам i-й элемент
можно выбрать

способами. Таким образом, число
перестановок, где хотя бы по одному
элементу стоит на своём месте, равно

.

Число перестановок, где i-й элемент
стоит на i-м месте, а j-й на j-м
(ij), равно
(n-2)!, при этом i-й и j-й элементы
можно выбрать

способами. Таким образом, число
перестановок, где хотя бы два элемента
стоят на своих местах –

.

Аналогично, число перестановок, где на
своих местах стоят хотя бы три элемента
–

.
Число перестановок, где на своих местах
стоят хотя бы r элементов
–

.
Число перестановок, где все элементы
стоят на своих местах

.
Подставляем в формулу решета:

#

Следствие 1.

Так как

,

то

.

Следствие 2.

Так как

,
то

.

Следствие 3.

Рекуррентная формула для числа
беспорядков:

.

#

#

Следствие 4.

# По рекуррентной формуле из следствия
3 получаем

или

.
При n=1 получаем

.
По формуле из следствия 1 получаем

.
Следовательно,

.
#

Следствие 5.

Ещё одна рекуррентная формула для числа
беспорядков:

.

# Рассмотрим n элементов x₁,
x₂, … , x_n.
Переставим их так, чтобы получить
беспорядок. Начнём с x₁: возьмём
x₁ и подставим его на место
i-го элемента (i1).
Тогда x_i можно поставить
на либо на первое место, либо на какое-то
другое, кроме i-го. Если x₁
стоит на i-м месте, а x_i
– на 1-ом, то число таких беспорядков –
D_n-2 (т.е. число
беспорядков оставшихся n-2 элементов).
Если x₁ не стоит на первом
месте, то такой беспорядок определяется
условием:

x₂ не стоит на 2-м месте,

x₃ не стоит на 3-м месте,

…

x_i-1 не
стоит на (i-1)-м месте,

x_i не стоит
на 1-м месте,

x_i+1
не стоит на (i+1)-м месте,

…

x_n не стоит
на n-м месте.

Всего здесь n-1 элемент,
то есть число таких беспорядков – D_n-1.

Итак, если x₁ стоит на i-ом
месте, то число таких беспорядков
D_n-1+D_n-2.
Но x₁ можно поставить на любое
из (n-1) мест (кроме 1-го). Для каждой
установки x₁ справедливы
приведённые выше рассуждения.

Таким образом, общее число беспорядков
– (n-1)(D_n-1+D_n-2).
#

Для проверки полученной формулы вычислим
количество беспорядков для некоторых
значений n по рекуррентной
и прямой формулам. По следствию 4, D₀=1,
D₁=0.

Рекуррентная формула	Нерекуррентная формула

Для строгого доказательства правильности
рекуррентной формулы, проверим ее в
общем виде.

.

Из следствия 3

,
следовательно,

.
Тогда

.
Подставим этот результат в рекуррентную
формулу:

.
Получили формулу из следствия 3.

Обозначим через D_n,r число
перестановок, в которых на своих местах
остаются r элементов,
а остальные (n-r) образуют беспорядок.
Ясно, что D_n,n=1 (все элементы
на своих местах), и D_n,0=D_n
(ни одного элемента нет на своём месте).

Теорема.

.

# r элементов, стоящих на своём месте,
можно выбрать из n элементов

способами. Для каждой такой выборки
остальные (n-r) элементов образуют
беспорядки, число которых D_n-r.
Следовательно, всего таких перестановок

.

С другой стороны, (n-r) элементов,
образующих беспорядки, можно выбрать

способами. Следовательно,

.
В силу симметричности биномиальных
коэффициентов

,
обе формулы дают один и тот же результат.

#

Пример. Выстраиваем 5 человек в
определённом порядке, после чего 3 из
них переставляем так, чтобы они не стояли
на своих местах. Сколько таких перестановок?

Ответ: если трое не стоят на своих местах,
то оставшиеся двое стоят на своих местах,
т.е.

.

Следствие.

.

# Из n элементов можно образовать
n! перестановок без повторений.

Среди них будет D_n,0 таких,
где ни один элемент не стоит на своём
месте;

D_n,1 таких, где по
одному элементу стоит на своём месте;

D_n,2 таких, где по паре
элементов стоит на своих местах;

и т.д.;

D_n,n=1 таких, где все элементы
стоят на своих местах.

Следовательно, общее число перестановок
(n!) равно сумме этих чисел. #

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Приветствую Вас, уважаемые Читатели! Сегодня хочу рассказать вам об одной математической операции, название которой кажется до боли знакомым, да и обозначение “!n” также никак не уводит в сторону от известного всем факториала n! = 1*2*3*…*n. Однако, у субфакториала есть свои особенности, да и смысл его использования в комбинаторике совсем другой. Посмотрим подробнее. Поехали!

Итак, если факториал определяет количество перестановок, возможных в наборе из n объектов, то субфакториал характеризует количество беспорядков в таком же наборе. Проще всего понять, что такое факториал на жизненном примере. Возьмем некоторое количество писем и конвертов и пронумеруем их:

Теперь наша задача в том, чтобы создать максимальный беспорядок, а именно сделать так, чтобы каждое письмо оказалось не в том конверте, для которого предназначено. На рисунке я показал один из способов такого распределения.

Вы уже, наверное, догадались, что именно субфакториал определит количество таких возможных перестановок, в комбинаторике называемых смещениями.

Формула для вычисления субфакториала сложностью не отличается:

Единственное, что восклицательный знак ставится перед переменной. Для примера вычислим !4:

Еще одна интерпретация задачи: профессор дал тест 4 студентам – 1, 2, 3 и 4 – и хочет, чтобы они оценили тесты друг друга. Конечно, ни один студент не должен оценивать свой собственный тест. Сколько существует способов, чтобы никто не получил обратно свой собственный тест для проверки?

Судя по формуле, субфакториал всегда меньше факториала, ведь в скобках величина всегда меньшая, чем 1/2 для n>3. Поразительно, но факториал и субфакторила лаконично связаны через постоянную Эйлера, и это действительно очень красиво:

Ну и напоследок еще одно феноменальное совпадение – единственное известное математикам число-субфакторион:

Спасибо за внимание! Не переставайте узнавать новое и тянуться к знаниям, даже если в этом нет сиюминутной практической пользы.

Читайте также:

Формула включения-исключения

Определение:

Формула включения-исключения (англ. Inclusion-exclusion principle) — комбинаторная формула, выражающая мощность объединения конечных множеств через мощности всех множеств и мощности всех их возможных пересечений.

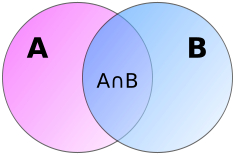
Для случая из двух множеств формула включения-исключения имеет следующий вид:

В силу того, что в сумме элементы пересечения учтены дважды, то уменьшаем текущее значение суммы на мощность пересечения, чтобы каждый элемент был подсчитан ровно один раз. Для наглядности воспользуемся диаграммой Эйлера—Венна для двух множеств, приведенной на рисунке справа.

Для случая с большим количеством рассматриваемых множеств процесс нахождения количества элементов объединения состоит в поочередном включений ошибочно исключенного и исключений ошибочно включенного. Отсюда и происходит название формулы.

Сформулируем и докажем теорему для нахождения мощности объединения произвольного количества множеств.

Теорема:

Пусть , тогда по формуле включения-исключения: Причем . Здесь за обозначим множество всех непустых подмножеств .

Доказательство:

Приведем два разноплановых доказательства теоремы. I. Комбинаторное доказательство теоремы. Рассмотрим некоторый элемент . Пусть . Тогда найдем число вхождений элемента в правую часть формулы. Докажем, что В силу того, что , имеем , то равенство доказано. Таким образом, , то есть каждый элемент подсчитан в правой части формулы ровно один раз, то теорема доказана. II. Доказательство теоремы по индукции. Пусть — это количество множеств, мощность пересечения которых мы ищем. Для случая равенство обращается в тривиальное ( — истинно). Для случая справедливость теоремы пояснена выше. Таким образом, — база индукции. Предположим, что для равенство верно. Докажем, что равенство истинно для Пусть — объединение множеств. Очевидно, что . Пусть ; . Исходя из предположения индукции, имеем, что Кроме того, так как формула верна для (из базы индукции), то верно равенство . Найдем : Очевидно, что Опираясь на предположение индукции и равенство имеем, что Подставим полученные значения в : Докажем, что Равенство справедливо, потому что все наборы можно разбить на две группы : Это означает, что в наборе точно не будет присутствовать индекс , а будут все различные варианты индексов остальных множеств, т.е. . , где Аналогично предыдущему, только в наборе будет индекс . Как видно из равенства, первое и третье слагаемое “отвечают” за вторую группу, а второе слагаемое за первую группу. Значит, равенство истинно и . Таким образом, для мы доказали, что равенство верно. Значит, индукционный переход верен, то есть теорема доказана.

Беспорядки

Определение:

Беспорядок (англ. Derangement) — это перестановка чисел от до , в которой ни один элемент не стоит на своём месте.

Явная формула с использованием принципа включения-исключения

Теорема:

Количество беспорядков порядка равно субфакториалу [1] числа (обозначение: ) и вычисляется по формуле:

Доказательство:

Воспользуемся принципом включения-исключения: обозначим за — количество перестановок из элементов, в каждой из которых -ый элемент стоит на своём месте. Тогда по формуле включения-исключения имеем: , где универсум — множество из всех перестановок порядка . — количество перестановок, в каждой из которых -ый элемент стоит не на своём -ом месте. Таким образом — количество всех перестановок, в каждой из которых -ый элемент ,то есть количество искомых беспорядков. , так как -ая позиция занята числом . — количество способов выбрать одну -ую позицию Рассмотрим , где . Так как некоторые позиций заняты соответствующими числами, то количество способов расставить остальные чисел равно . То есть Количество всех способов выбрать позиций равно . Таким образом получаем, что: Подставляя соответствующие значения мощностей множеств в формулу включения-исключения, получаем: Раскрывая по общеизвестной формуле, получим требуемое выражение, то есть количество беспорядков порядка .

Рекурретное соотношение для нахождения количества беспорядков

Утверждение:

Количество беспорядков удовлетворяет рекурсивным соотношениям: и , где , а

1) Докажем второе соотношение: Так как , то можно переписать эту формулу, как По формуле субфакториала 2) Докажем первое соотношение: У нас есть чисел и столько же мест. Мы должны найти количество способов разместить эти числа так, что ни одно из чисел не оказалось на месте с таким же номером. Предположим, что первое число оказалось на месте с номером . Это можно сделать способами, так как первое число может оказаться на любом месте, кроме первого. Теперь есть 2 варианта, зависящие от того, окажется ли число с номером на первом месте или нет. Число на первом месте. Остается мест и чисел. То есть количество беспорядков от Число не может оказаться на первом месте. Это эквивалентно решению задачи с местами и числами (первое число уже заняло место, а остальные еще нет): у каждого числа будет одно запрещенное место (у числа с номером запрещенным будет первое место). Получается количество беспорядков от . Эти 2 случая не пересекаются и поэтому суммируются. В первом случае число занимает первое место, затем идет распределение остальных чисел, не зависящее от первого и -го чисел. Во втором же случае число с номером попасть на первое место не может, а значит займет какое-то другое место, и распределение остальных чисел уже будет другое. В итоге получается необходимая формула.

Задача о перестановках

Сколько есть перестановок чисел от до таких, что первый элемент больше , а последний меньше ?

Посчитаем количество “плохих” перестановок, то есть таких, у которых первый элемент (множество таких перестановок обозначим ) и/или последний (множество таких перестановок обозначим ).

Тогда количество “плохих” перестановок по формуле включений-исключений равно:

Проведя несложные комбинаторные вычисления, получим:

Отнимая это число от общего числа перестановок , получим ответ.

Задача о нахождении числа взаимно простых четвёрок

Дано чисел: . Необходимо посчитать количество способов выбрать из них четыре числа так, что они будут взаимно простыми, то есть их НОД равен единице.

Посчитаем число “плохих” четвёрок, то есть таких, в которых все числа делятся на число .

Воспользуемся формулой включений-исключений, суммируя количество четвёрок, делящихся на (но, возможно, делящихся и на больший делитель).

,

где — это количество простых в факторизации числа , — количество четвёрок, делящихся на .

Чтобы посчитать функцию , надо просто посчитать количество чисел, кратных , и с помощью биномиальных коэффициентов посчитать число способов выбрать из них четвёрку.

Таким образом, с помощью формулы включений-исключений мы суммируем количество четвёрок, делящихся на простые числа, затем отнимаем число четвёрок, делящихся на произведение двух простых, прибавляем четвёрки, делящиеся на три простых, и т.д.

См. также

• Производящая функция
• Лемма Бёрнсайда и Теорема Пойа

Примечания

Источники информации

• Википедия — Беспорядок
• Wikipedia — Derangement
• Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика, Изд. 4-е, исправленное – МЦНМО, 2013 ISBN 978-5-4439-0052-0
• Р. Стенли, Перечислительная комбинаторика. — М.: Мир, 1990. — С. 107-108.

Задача о беспорядках и встречах