Компонентой связности неориентированного графа называется подмножество вершин, достижимых из какой-то заданной вершины. Как следствие неориентированности, все вершины компоненты связности достижимы друг из друга.
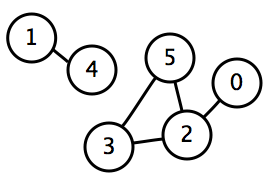
Дан неориентированный граф $G$ с $n$ вершинами и $m$ рёбрами. Требуется найти в нём все компоненты связности, то есть разбить вершины графа на несколько групп так, что внутри одной группы можно дойти от одной вершины до любой другой, а между разными группами путей не существует.
Для решения задачи модифицируем обход в глубину так, чтобы запустившись от вершины какой-то компоненты, от пометил все вершины этой компоненты — то есть все достижимые вершины — заданным номером этой компоненты. Для этого можно массив used заменить массивом номеров компонент для каждой вершины, изначально заполненный нулями:
const int maxn = 1e5;
int component[maxn]; // тут будут номера компонент
void dfs(int v, int num) {
component[v] = num;
for (int u : g[v])
if (!component[u]) // если номер не присвоен, то мы там ещё не были
dfs(u, num);
}
Теперь проведем серию обходов: сначала запустим обход из первой вершины, и все вершины, которые он при этом обошёл, образуют первую компоненту связности. Затем найдём первую из оставшихся вершин, которые ещё не были посещены, и запустим обход из неё, найдя тем самым вторую компоненту связности. И так далее, пока все вершины не станут помеченными.
Записывается это очень компактно:
int num = 0;
for (int v = 0; v < n; v++)
if (!component[v])
dfs(v, ++num);
После этого переменная num будет хранить число компонент связности, а массив component — номер компоненты для каждой вершины, который, например, можно использовать, чтобы быстро проверять, существует ли путь между заданной парой вершин.
Итоговая асимптотика составит $O(n + m)$, потому что такой алгоритм не будет запускаться от одной и той же вершины дважды, и каждое ребро будет просмотрено ровно два раза (с одного конца и с другого).
Вершины
xi
и xj
слабо связны,
если существует
путь (xi,
xj)
в графе
G=(X,E).
Вершины
xi
и
xj
сильно
связны,
если
существуют пути (xi,
xj)
и
(xj,
xi).
Если
в графе нет путей из xi
в xj
и нет обратного пути из xj
в xi,
то вершины xi
и xj
несвязны.
Для
неориентированного графа
имеет смысл только понятие сильной
связности.
Отношение
связности
рефлексивно,
симметрично, транзитивно,
т.
е. является
отношением
эквивалентности, и
однозначно разбивает множество вершин
графа на
компоненты связности: максимальные
подмножества сильно связанных между
собой вершин.
Пример
3.4: Задан
граф (рис.3.4). Найти его компоненты
связности.
Данный граф
может быть разбит на следующие компоненты
связности:
1){x1,x2,x3,x4};
2){x5,x6,x7};
3){x8}
Между компонентами
– только слабая связность: есть пути из
вершин 1-ой компоненты в вершины 2-ой и
3-ей компоненты, а также из вершин 2-ой
компоненты в вершину 3-ей.

Рис.
3.4
Алгоритм построения
компонент связности в неориентированном
графе
1.
i=0.
Все вершины графа не отмечены.
2.
i=i+1. Выбираем
очередную неотмеченную вершину, отмечаем
её и все связанные с нею вершины значением
индекса i
с помощью распространения волны отметок
по ребрам, идущих от уже отмеченных
индексом i
вершин. Таким
образом выделяется i
компонента связности. Если есть ещё
неотмеченные вершины, то выполняется
п.2, иначе выделение компонент связности
закончено.
8
Пример 3.9.

Рис.
3.9
3.5.1. Алгоритм построения произвольного остова
1.
Для каждой компоненты
i графа
выполняем пункты 2 и 3.
2. Строим
частичный подграф, содержащий все ni
вершин
i-й
компоненты и не содержащий ребер (0-
граф).
3.
Если в текущий частичный граф включены
уже ni–1
ребер, то
остов для компоненты i
построен, иначе выбираем очередное
ребро компоненты и пытаемся его включить
в текущий граф.
Если в текущем
графе это не приводит к образованию
цикла, то включаем ребро, иначе – не
включаем.
Ребро считаем
рассмотренным.
Выполняем пункт
3.
13
Пример
3.7
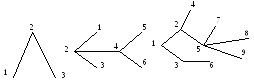
Рис.
3.7
Остов
– это подграф
(частичный граф), который может быть
построен из графа удалением некоторых
ребер и который является деревом.
В общем случае для
графа можно построить несколько остовов.
Для приведенного ниже графа построен
один из возможных вариантов остова.
Пример 3.8.

Рис.
3.8
Для несвязного
графа рассматриваются отдельные его
компоненты. Остов такого графа –
совокупность его компонент.
12
Пример
3.5

Рис. 3.5
Решение:
1. i=0
2.
i=1. Отмечаем индексом i=1 вершину
x1
и связанные с ней вершины
x3,
x7
и
x9.
Получена первая компонента связности:
k1
{x1,x3,x7,x9
}
2.
i=2.
Отметим индексом i=2
вершину x2
и вершины x6,x10![]() .
.
Построена вторая компонента связности:k2
{x2,x6,x10}
2.
i=3.
Отмечаются индексом i=3
вершины x4
и x8
. Построена третья компонента связности:
k3
{x4,
x8
}.
2.
i=4.
Отмечаются индексом i=4
вершину
x5,
которая формирует четвертую компоненту
связности – k4
{x5}
3.4. Алгоритмы
нахождения подграфов
Циклом
называется
замкнутый маршрут в неориентированном
графе. Для ориентированного графа
определяется аналогично понятие контур
– замкнутый
путь.
9
Пример
3.6.
В графе
(рис.3.6) каждому ребру присвоен свой
номер. Выделим соответствующее ему
число циклов. Для нашего примера циклами
Ci
являются замкнутые маршруты, образованные
ребрами :
C1={1,
2, 5, 4}, C2={5,
6, 7}, C3={3,
6, 2}, C4={1,
2, 6, 7, 4} и т. д. Среди этих циклов найдутся
такие, которые включают в себя другие
циклы. Так, цикл C4
состоит из
циклов C1
и C2 ,
у которых имеется общее ребро 5, не
вошедшее в цикл 4. Говорят, что цикл 4
получен линейной комбинацией циклов 1
и 2, т. е. является линейно зависимым от
них.
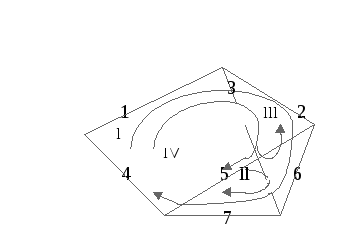
Рис. 3.6
Линейнозависимым
от некоторой совокупности других циклов
называется цикл,
который
можно построить линейной
комбинацией циклов
в этой совокупности.
П рисвоим
рисвоим
каждому ребру графа номерj,
j=1,m
и сопоставим
каждому циклу Сi
двоичный
m-разрядный
вектор Vi
,
компоненты
vij
которого
определяются следующим образом:
vij
=
0, если
ребро j
не входит в цикл
Ci
, vij
= 1 – в противном случае.
Тогда
линейной комбинацией векторов Vi
является
результат векторной
операции сложения по модулю два
этих векторов.
Поскольку
Vi
–
отношение принадлежности рёбер графа
циклу
Ci
,
а Ci
–
это множество
рёбер,
то в
результате применения векторной операции
![]() мы получаем совокупность рёбер, входящих
мы получаем совокупность рёбер, входящих
в циклы, составляющих линейную комбинацию
за исключением общих для этих циклов
рёбер.
10
На
языке теории множеств это означает
объединение множеств Ci
без их
пересечения, что соответствует операции
«симметрическая
разность»
двух множеств.
|
j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
V1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|||||||
|
V2 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
V4 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
В нашем примере
общим является ребро 5, которое исключено
из цикла 4.
Линейно-независимым
от совокупности
других циклов называется цикл, который
не может быть построен линейной
комбинацией этих циклов.
Максимальное
множество линейно-независимых циклов
образует систему
независимых циклов;
мощность
этого
множества называется цикломатическим
числом. Это
число определяется по формуле Эйлера
=m-n+p
(3.2)
Соседние файлы в папке XLAM
- #
- #
Рассмотрим базовую задачу.
Условие:
Дан неориентированный граф G, имеющий N вершин и M ребер. Чтобы все рассмотренные подходы имели практических смысл, ограничим N<=1000.
Необходимо найти количество компонент связности данного графа. Формат входных данных: В первой строке входного файла находятся N и M, разделенные пробелом. Далее идет M строк, содержащих пару вершин, между которыми находится ребро. Вершины нумеруются с 1.
Формат выходных данный: В единственной строке выдать количество компонент связности графа.
Пример: 
input.txt
15 11
1 2
2 3
2 11
10 11
11 12
11 15
4 12
12 13
8 14
7 14
5 6
output.txt
4
Компонента связности неориентированного графа является подграф, в котором для любой пары вершин v и u существует путь. Между двумя различными компонентами связности не существует пути.
Задача стара, как мир. Но тем не менее сегодня покажу несколько подходов по ее решению.
1. Поиск в глубину(DFS)
Самое классическое решение. Даже комментировать особо нечего.
- const int SIZE = 1e3 + 10;
- vector<int> adj[SIZE];
- bool usd[SIZE];
- ...
- void dfs(int cur) {
- usd[cur] = true;
- for (int i=0;i<adj[cur].size();++i) {
- int nxt = adj[cur][i];
- if (!usd[nxt])
- dfs(nxt);
- }
- }
- int connected_components_amount_dfs() {
- int cnt = 0;
- for (int i=1; i<=n; ++i) {
- if (!usd[i]) {
- dfs(i);
- ++cnt;
- }
- }
- return cnt;
- }
* This source code was highlighted with Source Code Highlighter.
Граф храним в виде списка смежности(строка 2). Общая сложность решения $latex O(N + M)$.
Решение
2. DSU подобная структура(ленивый подход)
Будем делать конденсацию компоненты в одну вершину. Идея следующая: будем последовательно обрабатывать ребра. Каждая компонента связности будет представлена одной своей вершиной(титульная). При этом неважно какой. По ходу обработки ребер титульная вершина компонент может меняться.
В итоге для нахождения количества компонент связности нужно найти количество титульных вершин.
- const int SIZE = 1e3 + 10;
- int p[SIZE];
- bool usd[SIZE];
- ...
- int connected_components_amount_dsu() {
- scanf("%d %d", &n, &m);
- for (int i=1;i<=n;++i) {
- p[i] = i;
- }
- for (int i=0;i<m;++i) {
- scanf("%d %d", &f, &s);
- int par = p[f];
- for (int j=1;j<=n;++j) {
- if (p[j] == par)
- p[j] = p[s];
- }
- }
- for (int i=1;i<=n;++i)
- usd[p[i]] = true;
- int cnt = 0;
- for (int i=1;i<=n;++i) {
- if (usd[i]) ++cnt;
- }
- return cnt;
- }
* This source code was highlighted with Source Code Highlighter.
Заметим, что сам граф непосредственно вообще никак не хранится. Общая сложность $latex O(M*N)$
Решение
3. Система непересекающихся множеств (DSU)
Реализацию, представленную выше можно существенно усовершенствовать. При добавлении нового ребра будем “мерджить меньшее подмножество к большему” + сжимать пути. У emaxx’а рассматривается доказательство того, что ассимптотика обработки одного ребра равна $latex O(alpha (N))$, где $latex alpha (N)$ – обратная функция Аккермана.
- const int SIZE = 1e3 + 10;
- int p[SIZE];
- int size[SIZE];
- int par(int x) {
- return p[x] == x ? x : p[x] = par(p[x]);
- }
- int connected_components_amount_dsu() {
- scanf("%d %d", &n, &m);
- for (int i=1;i<=n;++i) {
- p[i] = i;
- size[i] = 1;
- }
- for (int i=0;i<m;++i) {
- scanf("%d %d", &f, &s);
- f = par(f); s = par(s);
- if (f != s) {
- if (size[f] > size[s])
- swap(f,s);
- p[f] = s;
- size[s] += size[f];
- }
- }
- bool usd[SIZE];
- memset(usd, 0, sizeof(usd));
- for (int i=1;i<=n;++i)
- usd[par(i)] = true;
- int cnt = 0;
- for (int i=1;i<=n;++i) {
- if (usd[i]) ++cnt;
- }
- return cnt;
- }
* This source code was highlighted with Source Code Highlighter.
Как и прежде сам граф не хранится в виде матрицы смежности. Общая сложность $latex O(M * alpha (N))$
4. Алгоритм Флойда.
Этот подход для самых ленивых, правда он требует хранить граф явно в виде матрицы смежности.
Запускаем алгоритм Флойда и строим матрицу достижимости для каждой пары вершин. В результате если первоначально adj[u][v] указывало на наличие ребра между u и v, то после работы алгоритма adj[u][v] будет указывать на наличие пути между u и v. После чего можно написать DFS двумя вложенными циклами.
- const int SIZE = 1e3 + 10;
- int adj[SIZE][SIZE];
- bool usd[SIZE];
- ...
- int connected_components_amount_floyd() {
- for (int k=1;k<=n;++k){
- for (int i=1;i<=n;++i){
- for (int j=1;j<=n;++j){
- if (adj[i][k] + adj[k][j] == 2)
- adj[i][j] = 1;
- }
- }
- }
- int cnt = 0;
- for (int i=1;i<=n;++i) {
- if (!usd[i]) {
- ++cnt;
- usd[i] = true;
- for (int j=1;j<=n;++j) {
- if (adj[i][j] && !usd[j])
- usd[j] = true;
- }
- }
- }
- return cnt;
- }
* This source code was highlighted with Source Code Highlighter.
Алгоритм ужасно долгий, но зато пишется довольно просто. Общая сложность $latex O({ N }^{ 3 }) $
Решение
Собственно пока и все. Мы рассмотрели 3 принципиально разных подхода. На маленьких ограничениях можно выбрать тот из них, что больше по душе.
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Число компонент связности
|
|
26/11/13 |
Здравствуйте.
|
|
|
|
|
Mihr |
Re: Число компонент связности
|
||
18/09/14 |
Этой информации совершенно не достаточно.
|
||
|
|
|||
|
ИСН |
Re: Число компонент связности
|
||
18/05/06 |
Нашёл: три.
|
||
|
|
|||
|
MAKSUS_87 |
Re: Число компонент связности
|
|
26/11/13 |
|
|
|
|
|
ИСН |
Re: Число компонент связности
|
||
18/05/06 |
Серьёзно? Максимум – число вершин, минимум – число вершин минус число рёбер, но не меньше одной.
|
||
|
|
|||
|
Mihr |
Re: Число компонент связности
|
||
18/09/14 |
MAKSUS_87 ,
|
||
|
|
|||
|
MAKSUS_87 |
Re: Число компонент связности
|
|
26/11/13 |
ИСН Ну допустим 10 вершин, 30 ребер, тогда ваше утверждение не верно.
|
|
|
|
|
ИСН |
Re: Число компонент связности
|
||
18/05/06 |
Моё утверждение верно, только оценка в нём – нестрогая . Вам строгую надо? Вам действительно надо это, а не число километров до Юпитера? Если да, то можно измыслить.
|
||
|
|
|||
|
ratay |
Re: Число компонент связности
|
|
21/08/13 |
А что такое компонента связности? Связность – это я понимаю. А компонента связности – это отдельный связный кусок? То есть и у дерева, и у цикла по одной компоненте? Растолкуйте. И мне полезно, и вам вреда не будет.
|
|
|
|
|
MAKSUS_87 |
Re: Число компонент связности
|
|
26/11/13 |
ИСН Да. Мне нужно при 10 вершинах и 30 ребрах. Подтолкните меня, пожалуйста, на правильную волну.
|
|
|
|
|
provincialka |
Re: Число компонент связности
|
||
18/01/13 |
ratay , вас в гугле забанили? Не надо отвлекать человека.
|
||
|
|
|||
|
ИСН |
Re: Число компонент связности
|
||
18/05/06 |
При 10 вершинах и 30 ребрах у нас компонент связности будет либо одна, либо две. Нижнюю границу я назвал точно: это
|
||
|
|
|||
|
provincialka |
Re: Число компонент связности
|
||
18/01/13 |
(to ИСН) ИСН , вы как-то необычайно конкретны. А где подход? Намек? У меня сеть барахлит, только собралась подсказку сформулировать – а тут такое!
|
||
|
|
|||
|
MAKSUS_87 |
Re: Число компонент связности
|
|
26/11/13 |
ИСН Честно говоря, не понял.
|
|
|
|
|
provincialka |
Re: Число компонент связности
|
||
18/01/13 |
MAKSUS_87 . Предположим, вы построили искомый граф с
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
 . Верхняя – что-то типа
. Верхняя – что-то типа  (это тоже не совсем точно, но уже почти).
(это тоже не совсем точно, но уже почти). компонентами связности. Внутри каждой компоненты можете добавить ребер, чтобы она стала полным графом. Общее число ребер графа не уменьшится, то есть будет не менее 30.
компонентами связности. Внутри каждой компоненты можете добавить ребер, чтобы она стала полным графом. Общее число ребер графа не уменьшится, то есть будет не менее 30. 