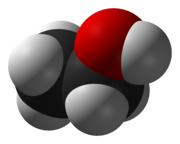
Изображение атома гелия, где плотность вероятности нахождения электрона представлена серым цветом, более тёмные области соответствуют большей плотности.
Ра́диус а́тома — расстояние между атомным ядром и самой дальней из стабильных орбит электронов в электронной оболочке этого атома. Поскольку, согласно квантовой механике, атомы не имеют четких границ, а вероятность найти электрон, связанный с ядром данного атома, на определённом расстоянии от этого ядра быстро убывает с увеличением расстояния, атому приписывают некоторый определённый радиус, полагая, что в шаре этого радиуса заключена подавляющая часть электронной плотности (порядка 90 процентов). Существуют различные определения радиуса атома[⇨], три наиболее широко используемых: радиус Ван-дер-Ваальса, ионный радиус и ковалентный радиус.
В зависимости от определения термин «радиус атома» может применяться либо только к изолированным атомам, либо также к атомам в конденсированной среде, ковалентно связанным в молекулах или в ионизированном и возбужденном состояниях; его значение может быть получено путем экспериментальных измерений или вычислено из теоретических моделей. Значение радиуса может зависеть от состояния атома и окружающей среды[1].
Электроны не имеют четко определённых орбит или границ. Скорее, их положения могут быть описаны как распределения вероятностей, которые постепенно сужаются по мере удаления от ядра без резкого сокращения. Кроме того, в конденсированном веществе и молекулах электронные облака атомов обычно в некоторой степени перекрываются, и некоторые из электронов могут перемещаться в области, охватывающей два или более атомов («принадлежать» нескольким атомам одновременно).
Согласно большинству определений, радиусы изолированных нейтральных атомов колеблются в диапазоне от 30 до 300 пм (или от 0,3 до 3 ангстрем), в то время как радиусы атомных ядер находятся пределах от 0,83 до 10 фм[2]. Следовательно, радиус типичного атома примерно в 30 тысяч раз больше радиуса его ядра.
Во многих случаях форма атома может быть аппроксимирована сферой. Это лишь грубое приближение, но оно может дать количественные представления и выступить в качестве базовой модели для описания для многих явлений, таких как плотность жидкостей и твердых веществ, диффузия жидкостей через молекулярные сита, расположение атомов и ионов в кристаллах, а также размер и форма молекул.
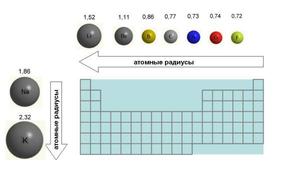
Радиусы атомов изменяются, подчиняясь определённым закономерностям периодической таблицы химических элементов. Например, радиусы атомов обычно уменьшаются при перемещении слева направо вдоль каждого периода (строки) таблицы, от щелочных металлов до благородных газов, и возрастают по мере продвижения сверху вниз в каждой группе (столбце). Радиусы атомов резко возрастают при переходе между благородным газом в конце каждого периода и щелочным металлом в начале следующего периода. Эти тенденции изменения радиусов атомов (наряду с другими химическими и физическими свойствами элементов) могут быть объяснены с точки зрения теории электронной оболочки атома, а также представляют доказательства подтверждения квантовой теории. Радиусы атомов уменьшаются в периодической таблице, потому что с увеличением атомного номера увеличивается число протонов в атоме, а дополнительные электроны добавляются в одну и ту же квантовую оболочку. Следовательно, эффективный заряд атомного ядра по отношению к внешним электронам увеличивается, притягивая внешние электроны. В результате электронное облако сжимается и атомный радиус уменьшается.
История[править | править код]
В 1920 году, вскоре после того, как стало возможным определять размеры атомов с помощью рентгеноструктурного анализа, было высказано предположение, что все атомы одного и того же элемента имеют одинаковые радиусы[3]. Однако в 1923 году, когда было получено больше данных о кристаллах, было обнаружено, что аппроксимация атома сферой не всегда корректна при сравнении атомов одного и того же элемента в разных кристаллических структурах[4].
Определения[править | править код]
Широко используемые определения радиуса атома включают:
- Радиус Ван-дер-Ваальса, Вандерваальсовы радиусы[5] — эта величина соответствует половине межъядерного расстояния между ближайшими одноимёнными атомами, не связанными между собой химической связью и принадлежащими разным молекулам (например, в молекулярных кристаллах).[6].
- Ионный радиус: номинальный радиус ионов элемента в определённом состоянии ионизации, выведенный из расстояния между атомными ядрами в кристаллических солях, которые включают эти ионы. В принципе, расстояние между двумя соседними противоположно заряженными ионами (длина ионной связи между ними) должно равняться сумме их ионных радиусов[6].
- Ковалентный радиус: номинальный радиус атомов элемента, когда они ковалентно связаны с другими атомами, выводится из расстояния между атомными ядрами в молекулах. В принципе, расстояние между двумя атомами, которые связаны друг с другом в молекуле (длина этой ковалентной связи), должно равняться сумме их ковалентных радиусов[6].
- Металлический радиус: номинальный радиус атомов элемента, когда они соединены с другими атомами металлическими связями.
- Боровский радиус: радиус орбиты электрона с наименьшей энергией, предсказанный Боровской моделью атома (1913)[7][8]. Он применим только к атомам и ионам с одним электроном, таким как водород, однократно ионизованный гелий и позитроний. Хотя сама модель в настоящее время устарела, радиус Бора для атома водорода считается одной из фундаментальных физических постоянных.
Измерение радиуса атома опытным путём[править | править код]
В таблице приведены измеренные опытным путём ковалентные радиусы для элементов, опубликованные американским химиком Д.Слейтером в 1964 году[9]. Значения приведены в пикометрах (пм или 1 × 10-12 м) с точностью около 5 пм. Оттенки цвета ячеек варьируются от красного до жёлтого по мере увеличения радиуса; серый цвет — отсутствие данных.
| Группы (столбцы) |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Периоды (строки) |
||||||||||||||||||
| 1 | H 25 |
He 31 |
||||||||||||||||
| 2 | Li 145 |
Be 105 |
B 85 |
C 70 |
N 65 |
O 60 |
F 50 |
Ne 38 |
||||||||||
| 3 | Na 180 |
Mg 150 |
Al 125 |
Si 110 |
P 100 |
S 100 |
Cl 100 |
Ar 71 |
||||||||||
| 4 | K 220 |
Ca 180 |
Sc 160 |
Ti 140 |
V 135 |
Cr 140 |
Mn 140 |
Fe 140 |
Co 135 |
Ni 135 |
Cu 135 |
Zn 135 |
Ga 130 |
Ge 125 |
As 115 |
Se 115 |
Br 115 |
Kr |
| 5 | Rb 235 |
Sr 200 |
Y 180 |
Zr 155 |
Nb 145 |
Mo 145 |
Tc 135 |
Ru 130 |
Rh 135 |
Pd 140 |
Ag 160 |
Cd 155 |
In 155 |
Sn 145 |
Sb 145 |
Te 140 |
I 140 |
Xe |
| 6 | Cs 260 |
Ba 215 |
* |
Hf 155 |
Ta 145 |
W 135 |
Re 135 |
Os 130 |
Ir 135 |
Pt 135 |
Au 135 |
Hg 150 |
Tl 190 |
Pb 180 |
Bi 160 |
Po 190 |
At |
Rn |
| 7 | Fr |
Ra 215 |
** |
Rf |
Db |
Sg |
Bh |
Hs |
Mt |
Ds |
Rg |
Cn |
Nh |
Fl |
Mc |
Lv |
Ts |
Og |
| Лантаноиды | * |
La 195 |
Ce 185 |
Pr 185 |
Nd 185 |
Pm 185 |
Sm 185 |
Eu 185 |
Gd 180 |
Tb 175 |
Dy 175 |
Ho 175 |
Er 175 |
Tm 175 |
Yb 175 |
Lu 175 |
||
| Актиноиды | ** |
Ac 195 |
Th 180 |
Pa 180 |
U 175 |
Np 175 |
Pu 175 |
Am 175 |
Cm |
Bk |
Cf |
Es |
Fm |
Md |
No |
Lr |
||
Объяснение общих тенденций[править | править код]
Изменение радиуса атома с увеличением зарядового числа можно объяснить расположением электронов в оболочках с постоянной ёмкостью. Оболочки обычно заполнены в порядке увеличения радиуса, поскольку отрицательно заряженные электроны притягиваются положительно заряженными протонами атомного ядра. Поскольку зарядовое число увеличивается вдоль каждой строки периодической таблицы, дополнительные электроны входят в ту же самую внешнюю оболочку, а её радиус постепенно сжимается из-за увеличения заряда ядра. В атомах инертных газов внешняя оболочка полностью заполнена; следовательно, дополнительный электрон следующего элемента — щелочного металла — перейдет в следующую внешнюю оболочку, что объясняет внезапное увеличение атомного радиуса.
Увеличивающийся заряд ядра частично уравновешивается ростом числа электронов, это явление известно как экранирование[en]; он объясняет, почему размер атомов обычно увеличивается в каждом столбце периодической таблицы. Из этой закономерности есть важное исключение, известное как лантаноидное сжатие: меньшие, по сравнению с ожидаемыми, величины ионных радиусов химических элементов, входящих в группу лантаноидов (атомный номер 58—71), которое происходит из-за недостаточного экранирования заряда ядра электронами 4f-орбитали.
По существу, атомный радиус уменьшается на протяжении периодов из-за увеличения количества протонов в ядре. Соответственно, большее количество протонов создает более сильный заряд и сильнее притягивает электроны, уменьшая размер радиуса атома. При движении сверху вниз по столбцам (группам) периодической таблицы атомный радиус увеличивается, поскольку есть больше энергетических уровней и, следовательно, больше расстояние между протонами и электронами. Кроме того, электронное экранирование ослабляет притяжение протонов, поэтому оставшиеся электроны могут удаляться от положительно заряженного ядра. Таким образом, размер (радиус атома) увеличивается.
В следующей таблице приведены основные факторы, влияющие радиус атома:
| Фактор | Закон | Возрастает с… | как правило | Влияние на радиус атома |
|---|---|---|---|---|
| Электронные оболочки | Квантовая механика | Главным и азимутальным квантовым числом | Увеличивает радиус атома | Возрастает сверху вниз в каждой колонке |
| Атомный заряд | Притяжение электронов протонами ядра атома | Зарядовым числом | Сокращает радиус атома | Сокращается в течение всего периода |
| Экранирование | Отталкивание внешних электронов внутренними электронами | Количеством электронов во внутренних оболочках | Увеличивает радиус атома | Снижает эффект второго фактора |
Лантаноидное сжатие[править | править код]
У химических элементов группы лантаноидов электроны в 4f-подоболочке, которая постепенно заполняется от церия (Z = 58) до лютеция (Z = 71), не особенно эффективны для экранирования увеличивающегося заряда ядра. Элементы, следующие непосредственно за лантаноидами, имеют радиусы атомов, которые меньше, чем можно было бы ожидать, и которые почти идентичны атомным радиусам элементов, находящихся непосредственно над ними[10]. Следовательно, гафний имеет практически тот же атомный радиус (и химические свойства), что и цирконий, а тантал имеет радиус атома, как у ниобия, и так далее. Эффект лантаноидного сжатия заметен вплоть до платины (Z = 78), после чего он нивелируется релятивистским эффектом, известным как эффект инертной пары[en].
Лантаноидное сжатие даёт 5 следующих эффектов:
- Размер ионов Ln3 + регулярно уменьшается с атомным номером. Согласно правилам Фаянса[en], уменьшение размера ионов Ln3+ увеличивает ковалентную связь и уменьшает основную связь между ионами Ln3+ и OH− в Ln(OH)3 до такой степени, что Yb(OH)3 и Lu(OH)3 с трудом растворяются в горячем концентрированном NaOH. Отсюда порядок размера ионов Ln3+:
La3+ > Ce3+ > …, … > Lu3+. - Наблюдается регулярное уменьшение ионных радиусов.
- Наблюдается регулярное снижение способности ионов действовать в качестве восстановителя с увеличением атомного номера.
- Второй и третий ряды переходных элементов d-блока довольно близки по свойствам.
- Эти элементы встречаются вместе в природных минералах и их трудно разделить.
d-сжатие[править | править код]
d-сжатие[en] менее выражено, чем лантаноидное сжатие, но возникает по той же причине. В этом случае плохая экранирующая способность 3d-электронов влияет на атомные радиусы и химические свойства элементов, следующих непосредственно за первым рядом переходных металлов, от галлия (Z = 30) до брома (Z = 35)[10].
Вычисленные радиусы атомов[править | править код]
В таблице приведены значения радиусов атомов, рассчитанные по теоретическим моделям, опубликованные итальянским химиком Энрико Клементи[en] и другими в 1967 году[11]. Значения даны в пикометрах (пм).
| Группы (столбцы) |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Периоды (строки) |
||||||||||||||||||
| 1 | H 53 |
He 31 |
||||||||||||||||
| 2 | Li 167 |
Be 122 |
B 87 |
C 67 |
N 56 |
O 48 |
F 42 |
Ne 38 |
||||||||||
| 3 | Na 190 |
Mg 145 |
Al 118 |
Si 111 |
P 98 |
S 88 |
Cl 79 |
Ar 71 |
||||||||||
| 4 | K 243 |
Ca 194 |
Sc 184 |
Ti 176 |
V 171 |
Cr 166 |
Mn 161 |
Fe 156 |
Co 152 |
Ni 149 |
Cu 145 |
Zn 142 |
Ga 136 |
Ge 125 |
As 114 |
Se 103 |
Br 94 |
Kr 98 |
| 5 | Rb 265 |
Sr 219 |
Y 212 |
Zr 206 |
Nb 198 |
Mo 190 |
Tc 183 |
Ru 178 |
Rh 173 |
Pd 169 |
Ag 165 |
Cd 161 |
In 156 |
Sn 145 |
Sb 133 |
Te 123 |
I 115 |
Xe 108 |
| 6 | Cs 298 |
Ba 253 |
* | Hf 208 |
Ta 200 |
W 193 |
Re 188 |
Os 185 |
Ir 180 |
Pt 177 |
Au 174 |
Hg 171 |
Tl 156 |
Pb 154 |
Bi 143 |
Po 135 |
At 127 |
Rn 120 |
| 7 | Fr |
Ra |
** | Rf |
Db |
Sg |
Bh |
Hs |
Mt |
Ds |
Rg |
Cn |
Nh |
Fl |
Mc |
Lv |
Ts |
Og |
| Лантаноиды | * | La 226 |
Ce 210 |
Pr 247 |
Nd 206 |
Pm 205 |
Sm 238 |
Eu 231 |
Gd 233 |
Tb 225 |
Dy 228 |
Ho 226 |
Er 226 |
Tm 222 |
Yb 222 |
Lu 217 |
||
| Актиноиды | ** | Ac |
Th |
Pa |
U |
Np |
Pu |
Am |
Cm |
Bk |
Cf |
Es |
Fm |
Md |
No |
Lr |
||
См. также[править | править код]
- Боровский радиус
- Ковалентный радиус
- Радиус Ван-дер-Ваальса
- Ионный радиус
- Химическая связь
Примечания[править | править код]
- ↑
Cotton, F. A.; Wilkinson, G. Advanced Inorganic Chemistry (неопр.). — 5th. — Wiley, 1988. — С. 1385. — ISBN 978-0-471-84997-1. - ↑
Basdevant, J.-L.; Rich, J.; Spiro, M. Fundamentals in Nuclear Physics (неопр.). — Springer, 2005. — С. 13, fig 1.1. — ISBN 978-0-387-01672-6. - ↑
Bragg, W. L. The arrangement of atoms in crystals (англ.) // Philosophical Magazine : journal. — 1920. — Vol. 6, no. 236. — P. 169—189. — doi:10.1080/14786440808636111. - ↑
Wyckoff, R. W. G. On the Hypothesis of Constant Atomic Radii (англ.) // Proceedings of the National Academy of Sciences of the United States of America : journal. — 1923. — Vol. 9, no. 2. — P. 33—38. — doi:10.1073/pnas.9.2.33. — Bibcode: 1923PNAS….9…33W. — PMID 16576657. — PMC 1085234. - ↑ Такое написание даёт «Русский орфографический словарь: около 200 000 слов / Российская академия наук. Институт русскоrо языка им. В. В. Виноградова / Под ред. В. В. Лопатина, О. Е. Ивановой. — Изд. 4-е, испр. и доп. — М.: АСТ-ПРЕСС КНИГА, 2013. — 896 с. — (Фундаментальные словари русскою языка). — с. 68. — ISBN 978-5-462-01272-3».
- ↑ 1 2 3
L.; Pauling. The Nature of the Chemical Bond (неопр.). — 2nd. — Cornell University Press, 1945. - ↑
Bohr, N. On the Constitution of Atoms and Molecules, Part I. – Binding of Electrons by Positive Nuclei (англ.) // Philosophical Magazine : journal. — 1913. — Vol. 26, no. 151. — P. 1—24. — doi:10.1080/14786441308634955. - ↑
Bohr, N. On the Constitution of Atoms and Molecules, Part II. – Systems containing only a Single Nucleus (англ.) // Philosophical Magazine : journal. — 1913. — Vol. 26, no. 153. — P. 476—502. — doi:10.1080/14786441308634993. - ↑
Slater, J. C. Atomic Radii in Crystals (англ.) // Journal of Chemical Physics : journal. — 1964. — Vol. 41, no. 10. — P. 3199—3205. — doi:10.1063/1.1725697. — Bibcode: 1964JChPh..41.3199S. - ↑ 1 2
W. L.; Jolly. Modern Inorganic Chemistry (неопр.). — 2nd. — McGraw-Hill Education, 1991. — С. 22. — ISBN 978-0-07-112651-9. - ↑
Clementi, E.; Raimond, D. L.; Reinhardt, W. P. Atomic Screening Constants from SCF Functions. II. Atoms with 37 to 86 Electrons (англ.) // Journal of Chemical Physics : journal. — 1967. — Vol. 47, no. 4. — P. 1300—1307. — doi:10.1063/1.1712084. — Bibcode: 1967JChPh..47.1300C.
Литература[править | править код]
- Рабинович В. А., Хавин З.Я. Краткий химический справочник. Изд. 2-е, испр. и доп. — Л.: Химия, 1978. — 392 с.
Как определить радиус атома
Под радиусом атома понимается расстояние между ядром данного атома и его самой дальней электронной орбитой. На сегодняшний день общепринятой единицей измерения атомного радиуса является пикометр(пм). Определить радиус атома очень легко.

Вам понадобится
- Периодическая таблица Менделеева
Инструкция
Первым делом, под рукой должна иметься обычная таблица Менделеева, в которой по порядку расставлены все известные человечеству химические элементы. Найти эту таблицу очень легко в любом справочнике по химии, школьном учебнике, либо же ее можно приобрести отдельно, в ближайшем книжном магазине.
В правом верхнем углу у каждого из химических элементов указан его порядковый номер. Этот номер полностью совпадает с атомным радиусом данного атома.
Например, порядковый номер хлора (Cl) – 17. Это означает, что расстояние от ядра атома хлора до самой дальней его орбиты движения стабильного электрона равно 17 пм. Если требуется найти не только атомный радиус, но и распределение электронов по электронным орбитам, то эти данные можно подчеркнуть из столбика цифр, расположенного справа от названия химического элемента.
Обратите внимание
Благодаря таблице Менделеева, очень легко найти не только атомный радиус, но и атомную массу, молекулярную массу, период и ряд того или иного элемента, а также и распределение электронов по электронным орбитам вместе с количеством орбит.
Наиболее популярной моделью атома является модель, принятая в 1913 году Нильсом Бором. Также она известна как планетарная модель. Связано это с тем, что электроны, подобно планетам Солнечной системы, движутся вокруг Солнца – ядра атома. Орбиты движения электронов постоянны. Разработка данной модели дала толчок к развитию нового направления в теоретической физике – квантовой механике.
Самый первый радиус орбиты движения электрона называется боровским радиусом, а энергия электронов на первой орбите называется энергией ионизации атома.
Полезный совет
Стоит отметить, что радиус любого атома обратно пропорционален количеству протонов в его ядре, а также равен заряду его ядра.
Источники:
- как изменяется радиус атома
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
From Wikipedia, the free encyclopedia
Diagram of a helium atom, showing the electron probability density as shades of gray.
The atomic radius of a chemical element is a measure of the size of its atom, usually the mean or typical distance from the center of the nucleus to the outermost isolated electron. Since the boundary is not a well-defined physical entity, there are various non-equivalent definitions of atomic radius. Four widely used definitions of atomic radius are: Van der Waals radius, ionic radius, metallic radius and covalent radius. Typically, because of the difficulty to isolate atoms in order to measure their radii separately, atomic radius is measured in a chemically bonded state; however theoretical calculations are simpler when considering atoms in isolation. The dependencies on environment, probe, and state lead to a multiplicity of definitions.
Depending on the definition, the term may apply to atoms in condensed matter, covalently bonding in molecules, or in ionized and excited states; and its value may be obtained through experimental measurements, or computed from theoretical models. The value of the radius may depend on the atom’s state and context.[1]
Electrons do not have definite orbits nor sharply defined ranges. Rather, their positions must be described as probability distributions that taper off gradually as one moves away from the nucleus, without a sharp cutoff; these are referred to as atomic orbitals or electron clouds. Moreover, in condensed matter and molecules, the electron clouds of the atoms usually overlap to some extent, and some of the electrons may roam over a large region encompassing two or more atoms.
Under most definitions the radii of isolated neutral atoms range between 30 and 300 pm (trillionths of a meter), or between 0.3 and 3 ångströms. Therefore, the radius of an atom is more than 10,000 times the radius of its nucleus (1–10 fm),[2] and less than 1/1000 of the wavelength of visible light (400–700 nm).
For many purposes, atoms can be modeled as spheres. This is only a crude approximation, but it can provide quantitative explanations and predictions for many phenomena, such as the density of liquids and solids, the diffusion of fluids through molecular sieves, the arrangement of atoms and ions in crystals, and the size and shape of molecules.[citation needed]
History[edit]
In 1920, shortly after it had become possible to determine the sizes of atoms using X-ray crystallography, it was suggested that all atoms of the same element have the same radii.[3] However, in 1923, when more crystal data had become available, it was found that the approximation of an atom as a sphere does not necessarily hold when comparing the same atom in different crystal structures.[4]
Definitions[edit]
Widely used definitions of atomic radius include:
- Van der Waals radius: In the simplest definition, half the minimum distance between the nuclei of two atoms of the element that are not otherwise bound by covalent or metallic interactions.[5] The Van der Waals radius may be defined even for elements (such as metals) in which Van der Waals forces are dominated by other interactions. Because Van der Waals interactions arise through quantum fluctuations of the atomic polarisation, the polarisability (which can usually be measured or calculated more easily) may be used to define the Van der Waals radius indirectly.[6]
- Ionic radius: the nominal radius of the ions of an element in a specific ionization state, deduced from the spacing of atomic nuclei in crystalline salts that include that ion. In principle, the spacing between two adjacent oppositely charged ions (the length of the ionic bond between them) should equal the sum of their ionic radii.[5]
- Covalent radius: the nominal radius of the atoms of an element when covalently bound to other atoms, as deduced from the separation between the atomic nuclei in molecules. In principle, the distance between two atoms that are bound to each other in a molecule (the length of that covalent bond) should equal the sum of their covalent radii.[5]
- Metallic radius: the nominal radius of atoms of an element when joined to other atoms by metallic bonds.[citation needed]
- Bohr radius: the radius of the lowest-energy electron orbit predicted by Bohr model of the atom (1913).[7][8] It is only applicable to atoms and ions with a single electron, such as hydrogen, singly ionized helium, and positronium. Although the model itself is now obsolete, the Bohr radius for the hydrogen atom is still regarded as an important physical constant.
Empirically measured atomic radius[edit]
The following table shows empirically measured covalent radii for the elements, as published by J. C. Slater in 1964.[9] The values are in picometers (pm or 1×10−12 m), with an accuracy of about 5 pm. The shade of the box ranges from red to yellow as the radius increases; gray indicates lack of data.
| Group (column) |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| Period (row) |
|||||||||||||||||||
| 1 | H 25 |
He |
|||||||||||||||||
| 2 | Li 145 |
Be 105 |
B 85 |
C 70 |
N 65 |
O 60 |
F 50 |
Ne |
|||||||||||
| 3 | Na 180 |
Mg 150 |
Al 125 |
Si 110 |
P 100 |
S 100 |
Cl 100 |
Ar |
|||||||||||
| 4 | K 220 |
Ca 180 |
Sc 160 |
Ti 140 |
V 135 |
Cr 140 |
Mn 140 |
Fe 140 |
Co 135 |
Ni 135 |
Cu 135 |
Zn 135 |
Ga 130 |
Ge 125 |
As 115 |
Se 115 |
Br 115 |
Kr |
|
| 5 | Rb 235 |
Sr 200 |
Y 180 |
Zr 155 |
Nb 145 |
Mo 145 |
Tc 135 |
Ru 130 |
Rh 135 |
Pd 140 |
Ag 160 |
Cd 155 |
In 155 |
Sn 145 |
Sb 145 |
Te 140 |
I 140 |
Xe |
|
| 6 | Cs 260 |
Ba 215 |
* |
Lu 175 |
Hf 155 |
Ta 145 |
W 135 |
Re 135 |
Os 130 |
Ir 135 |
Pt 135 |
Au 135 |
Hg 150 |
Tl 190 |
Pb 180 |
Bi 160 |
Po 190 |
At |
Rn |
| 7 | Fr |
Ra 215 |
** |
Lr |
Rf |
Db |
Sg |
Bh |
Hs |
Mt |
Ds |
Rg |
Cn |
Nh |
Fl |
Mc |
Lv |
Ts |
Og |
| * |
La 195 |
Ce 185 |
Pr 185 |
Nd 185 |
Pm 185 |
Sm 185 |
Eu 185 |
Gd 180 |
Tb 175 |
Dy 175 |
Ho 175 |
Er 175 |
Tm 175 |
Yb 175 |
|||||
| ** |
Ac 195 |
Th 180 |
Pa 180 |
U 175 |
Np 175 |
Pu 175 |
Am 175 |
Cm |
Bk |
Cf |
Es |
Fm |
Md |
No |
|||||
Explanation of the general trends[edit]
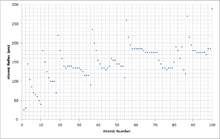
A graph comparing the atomic radius of elements with atomic numbers 1–100. Accuracy of ±5 pm.
The way the atomic radius varies with increasing atomic number can be explained by the arrangement of electrons in shells of fixed capacity. The shells are generally filled in order of increasing radius, since the negatively charged electrons are attracted by the positively charged protons in the nucleus. As the atomic number increases along each row of the periodic table, the additional electrons go into the same outermost shell; whose radius gradually contracts, due to the increasing nuclear charge. In a noble gas, the outermost shell is completely filled; therefore, the additional electron of next alkali metal will go into the next outer shell, accounting for the sudden increase in the atomic radius.
The increasing nuclear charge is partly counterbalanced by the increasing number of electrons, a phenomenon that is known as shielding; which explains why the size of atoms usually increases down each column. However, there is one notable exception, known as the lanthanide contraction: the 5d block of elements are much smaller than one would expect, due to the weak shielding of the 4f electrons.
Essentially, the atomic radius decreases across the periods due to an increasing number of protons. Therefore, there is a greater attraction between the protons and electrons because opposite charges attract, and more protons create a stronger charge. The greater attraction draws the electrons closer to the protons, decreasing the size of the particle. Therefore, the atomic radius decreases. Down the groups, atomic radius increases. This is because there are more energy levels and therefore a greater distance between protons and electrons. In addition, electron shielding causes attraction to decrease, so remaining electrons can go farther away from the positively charged nucleus. Therefore, the size, or atomic radius, increases.
The following table summarizes the main phenomena that influence the atomic radius of an element:
| factor | principle | increase with… | tend to | effect on radius |
|---|---|---|---|---|
| electron shells | quantum mechanics | principal and azimuthal quantum numbers | increase down each column | increases the atomic radius |
| nuclear charge | attractive force acting on electrons by protons in nucleus | atomic number | increase along each period (left to right) | decreases the atomic radius |
| shielding | repulsive force acting on outermost shell electrons by inner electrons | number of electrons in inner shells | reduce the effect of the 2nd factor | increases the atomic radius |
Lanthanide contraction[edit]
The electrons in the 4f-subshell, which is progressively filled from lanthanum (Z = 57) to ytterbium (Z = 70), are not particularly effective at shielding the increasing nuclear charge from the sub-shells further out. The elements immediately following the lanthanides have atomic radii which are smaller than would be expected and which are almost identical to the atomic radii of the elements immediately above them.[10] Hence lutetium is in fact slightly smaller than yttrium, hafnium has virtually the same atomic radius (and chemistry) as zirconium, and tantalum has an atomic radius similar to niobium, and so forth. The effect of the lanthanide contraction is noticeable up to platinum (Z = 78), after which it is masked by a relativistic effect known as the inert-pair effect.[citation needed]
Due to lanthanide contraction, the 5 following observations can be drawn:
- The size of Ln3+ ions regularly decreases with atomic number. According to Fajans’ rules, decrease in size of Ln3+ ions increases the covalent character and decreases the basic character between Ln3+ and OH− ions in Ln(OH)3, to the point that Yb(OH)3 and Lu(OH)3 can dissolve with difficulty in hot concentrated NaOH. Hence the order of size of Ln3+ is given:
La3+ > Ce3+ > …, … > Lu3+. - There is a regular decrease in their ionic radii.
- There is a regular decrease in their tendency to act as a reducing agent, with an increase in atomic number.
- The second and third rows of d-block transition elements are quite close in properties.
- Consequently, these elements occur together in natural minerals and are difficult to separate.
d-block contraction[edit]
The d-block contraction is less pronounced than the lanthanide contraction but arises from a similar cause. In this case, it is the poor shielding capacity of the 3d-electrons which affects the atomic radii and chemistries of the elements immediately following the first row of the transition metals, from gallium (Z = 31) to bromine (Z = 35).[10]
Calculated atomic radius[edit]
The following table shows atomic radii computed from theoretical models, as published by Enrico Clementi and others in 1967.[11] The values are in picometres (pm).
| Group (column) |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| Period (row) |
|||||||||||||||||||
| 1 | H 53 |
He 31 |
|||||||||||||||||
| 2 | Li 167 |
Be 112 |
B 87 |
C 67 |
N 56 |
O 48 |
F 42 |
Ne 38 |
|||||||||||
| 3 | Na 190 |
Mg 145 |
Al 118 |
Si 111 |
P 98 |
S 88 |
Cl 79 |
Ar 71 |
|||||||||||
| 4 | K 243 |
Ca 194 |
Sc 184 |
Ti 176 |
V 171 |
Cr 166 |
Mn 161 |
Fe 156 |
Co 152 |
Ni 149 |
Cu 145 |
Zn 142 |
Ga 136 |
Ge 125 |
As 114 |
Se 103 |
Br 94 |
Kr 88 |
|
| 5 | Rb 265 |
Sr 219 |
Y 212 |
Zr 206 |
Nb 198 |
Mo 190 |
Tc 183 |
Ru 178 |
Rh 173 |
Pd 169 |
Ag 165 |
Cd 161 |
In 156 |
Sn 145 |
Sb 133 |
Te 123 |
I 115 |
Xe 108 |
|
| 6 | Cs 298 |
Ba 253 |
* |
Lu 217 |
Hf 208 |
Ta 200 |
W 193 |
Re 188 |
Os 185 |
Ir 180 |
Pt 177 |
Au 174 |
Hg 171 |
Tl 156 |
Pb 154 |
Bi 143 |
Po 135 |
At 127 |
Rn 120 |
| 7 | Fr |
Ra |
** |
Lr |
Rf |
Db |
Sg |
Bh |
Hs |
Mt |
Ds |
Rg |
Cn |
Nh |
Fl |
Mc |
Lv |
Ts |
Og |
| * |
La 226 |
Ce 210 |
Pr 247 |
Nd 206 |
Pm 205 |
Sm 238 |
Eu 231 |
Gd 233 |
Tb 225 |
Dy 228 |
Ho 226 |
Er 226 |
Tm 222 |
Yb 222 |
|||||
| ** |
Ac |
Th |
Pa |
U |
Np |
Pu |
Am |
Cm |
Bk |
Cf |
Es |
Fm |
Md |
No |
See also[edit]
- Atomic radii of the elements (data page)
- Chemical bond
- Covalent radius
- Bond length
- Steric hindrance
- Kinetic diameter
Notes[edit]
- Difference between empirical and calculated data: Empirical data means “originating in or based on observation or experience” or “relying on experience or observation alone often without due regard for system and theory data”.[12] In other words, the data are measured through physical observation, and vetted by other experiments generating similar results. Calculated data, on the other hand, are derived from theoretical models. Such predictions are especially useful for elements whose radii cannot be measured experimentally (e.g. those that have not been discovered, or that have too short of a half-life).
References[edit]
- ^
Cotton, F. A.; Wilkinson, G. (1988). Advanced Inorganic Chemistry (5th ed.). Wiley. p. 1385. ISBN 978-0-471-84997-1. - ^
Basdevant, J.-L.; Rich, J.; Spiro, M. (2005). Fundamentals in Nuclear Physics. Springer. p. 13, fig 1.1. ISBN 978-0-387-01672-6. - ^
Bragg, W. L. (1920). “The arrangement of atoms in crystals”. Philosophical Magazine. 6. 40 (236): 169–189. doi:10.1080/14786440808636111. - ^
Wyckoff, R. W. G. (1923). “On the Hypothesis of Constant Atomic Radii”. Proceedings of the National Academy of Sciences of the United States of America. 9 (2): 33–38. Bibcode:1923PNAS….9…33W. doi:10.1073/pnas.9.2.33. PMC 1085234. PMID 16576657. - ^ a b c
Pauling, L. (1945). The Nature of the Chemical Bond (2nd ed.). Cornell University Press. LCCN 42034474. - ^
Federov, Dmitry V.; Sadhukhan, Mainak; Stöhr, Martin; Tkatchenko, Alexandre (2018). “Quantum-Mechanical Relation between Atomic Dipole Polarizability and the van der Waals Radius”. Physical Review Letters. 121 (18): 183401. arXiv:1803.11507. Bibcode:2018PhRvL.121r3401F. doi:10.1103/PhysRevLett.121.183401. PMID 30444421. S2CID 53564141. Retrieved 9 May 2021. - ^
Bohr, N. (1913). “On the Constitution of Atoms and Molecules, Part I. – Binding of Electrons by Positive Nuclei” (PDF). Philosophical Magazine. 6. 26 (151): 1–24. Bibcode:1913PMag…26….1B. doi:10.1080/14786441308634955. Archived (PDF) from the original on 2011-09-02. Retrieved 8 June 2011. - ^
Bohr, N. (1913). “On the Constitution of Atoms and Molecules, Part II. – Systems containing only a Single Nucleus” (PDF). Philosophical Magazine. 6. 26 (153): 476–502. Bibcode:1913PMag…26..476B. doi:10.1080/14786441308634993. Archived (PDF) from the original on 2008-12-09. Retrieved 8 June 2011. - ^
Slater, J. C. (1964). “Atomic Radii in Crystals”. Journal of Chemical Physics. 41 (10): 3199–3205. Bibcode:1964JChPh..41.3199S. doi:10.1063/1.1725697. - ^ a b
Jolly, W. L. (1991). Modern Inorganic Chemistry (2nd ed.). McGraw-Hill. p. 22. ISBN 978-0-07-112651-9. - ^
Clementi, E.; Raimond, D. L.; Reinhardt, W. P. (1967). “Atomic Screening Constants from SCF Functions. II. Atoms with 37 to 86 Electrons”. Journal of Chemical Physics. 47 (4): 1300–1307. Bibcode:1967JChPh..47.1300C. doi:10.1063/1.1712084. - ^ “Definition of EMPIRICAL”.
Чтобы разобраться в вопросе, что в современной науке называется радиусом атома, вспомним, что из себя представляет сам атом. По классическим представлениям в центре атома находится ядро, состоящее из протонов и нейтронов, а вокруг ядра каждый на своей орбите вращаются электроны.
Содержание:
- Радиус атома в физике
- Атомный радиус в химии и кристаллографии
- Какие бывают виды
- Как зависит от типа химической связи
- Видео
Радиус атома в физике
Поскольку в данной модели строения атома электроны являются пространственно ограниченными частицами, т. е. корпускулами, логично считать атомным радиусом (а. р.) расстояние от его ядра до самой дальней, или внешней, орбиты, по которой вращаются так называемые валентные электроны.
Однако по современным, квантовомеханическим представлениям, определить данный параметр нельзя так однозначно, как это делается в классической модели. Здесь электроны уже не представляются в виде частиц-корпускул, а получают свойства волн, т. е. пространственно-неограниченных объектов. В такой модели точно определить положение электрона просто невозможно. Здесь эта частица уже представляется в виде электронной орбитали, плотность которой меняется, в зависимости от расстояния до ядра атома.
Итак, в современной модели строения атома его радиус нельзя определить однозначно. Поэтому в квантовой физике, общей химии, физике твердого тела и других смежных науках эту величину сегодня определяют как радиус сферы, в центре которой находится ядро, внутри которой сосредоточено 90-98% плотности электронного облака. Фактически это расстояние и определяет границы атома.
Если рассмотреть Периодическую таблицу химических элементов (таблицу Менделеева), в которой приведены атомные радиусы, можно увидеть определенные закономерности, которые выражаются в том, что в пределах периода эти числа уменьшаются слева направо, а в пределах группы они увеличиваются сверху вниз. Такие закономерности объясняются тем, что внутри периода при движении слева направо заряд атома возрастает, что увеличивает силу притяжения им электронов, а при движении внутри группы сверху вниз все больше заполняется электронных оболочек.
Атомный радиус в химии и кристаллографии
Какие бывают виды
Данная характеристика сильно варьируется, в зависимости от того, в какой химической связи состоит атом. Поскольку все вещества в природе в подавляющем своем большинстве состоят из молекул, понятие а. р. используют для определения межатомных расстояний в молекуле. А данная характеристика зависит от свойств входящих в молекулу атомов, т. е. их положения в Периодической системе химических элементов. Обладая разными физическими и химическими свойствами, молекулы образуют все огромное разнообразие веществ.
По сути, эта величина очерчивает сферу действия силы электрического притяжения ядра атома и его внешних электронных оболочек. За пределами этой сферы в действие вступает сила электрического притяжения соседнего атома. Существует несколько типов химической связи атомов в молекуле:
- ковалентная;
- ионная;
- металлическая;
- ван-дер-ваальсова.
Соответственно этим связям таким же будет и атомный радиус.
Как зависит от типа химической связи
При ковалентной связи АР определяется как половина расстояния между соседними атомами в одинарной химической связи Х—Х, причем Х — это неметалл, ибо данная связь свойственна неметаллам. Например, для галогенов ковалентный радиус будет равен половине межъядерного расстояния Х—Х в молекуле Х2, для молекул селена Se и серы S — половине расстояния Х—Х в молекуле Х8, для углерода С он будет равен половине кратчайшего расстояния С—С в кристалле алмаза.
Данная химическая связь обладает свойством аддитивности, т. е. суммирования, что позволяет определять межъядерные расстояния в многоатомных молекулах. Если связь в молекуле двойная или тройная, то ковалентный АР уменьшается, т. к. длины кратных связей меньше одинарных.
При ионной связи, образующейся в ионных кристаллах, используют значения ионного АР для определения расстояния между ближайшими анионом и катионом, находящимися в узлах кристаллической решетки. Такое расстояние определяется как сумма радиусов этих ионов.
Существует несколько способов определения ионных радиусов, при которых отличаются значения у индивидуальных ионов. Но в результате эти способы дают примерно одинаковые значения межъядерных расстояний. Эти способы или системы были названы в честь ученых, проводивших в этой области соответствующие исследования:
- Гольдшмидта;
- Полинга;
- Белова и Бокия;
- других ученых.
При металлической связи, возникающей в кристаллах металлов, АР принимаются равными половине кратчайшего расстояния между ними. Металлический радиус зависит от координационного числа К. При К=12 его значение условно принимается за единицу. Для координационных чисел 4, 6 и 8 металлические радиусы одного и того же элемента соответственно будут равны 0.88, 0.96 и 0.98.
Если взять два разных металла и сравнить металлические радиусы их элементов, то близость этих значений друг к другу будет означать необходимое, но недостаточное условие взаимной растворимости этих металлов по типу замещения. Например, жидкие калий К и литий Li в обычных условиях не смешиваются и образуют два жидких слоя, потому что их металлические радиусы сильно различаются (0.236 нм и 0.155 нм соответственно), а калий К с цезием Cs образуют твердый раствор благодаря близости их радиусов (0.236 нм и 0.268 нм).
Ван-дер-ваальсовы АР используют для определения эффективных размеров атомов благородных газов, а также расстояний между ближайшими одноименными атомами, принадлежащими разным молекулам и не связанными химической связью (пример — молекулярные кристаллы). Если такие атомы сблизятся на расстояние, меньшее суммы их ван-дер-ваальсовых радиусов, между ними возникнет сильное межатомное отталкивание. Эти радиусы определяют минимально допустимые границы контакта двух атомов, принадлежащих соседним молекулам.
Кроме того, данные АР используют для определения формы молекул, их конформаций и упаковки в молекулярных кристаллах. Известен принцип “плотной упаковки”, когда молекулы, образующие кристалл, входят друг в друга своими “выступами” и “впадинами”. На основе этого принципа интерпретируются данные кристаллографии и предсказываются структуры молекулярных кристаллов.
Видео
Это полезное видео поможет вам понять, что такое радиус атома.
Ну, что ж, в рамках предыдущих 10! серий (вы можете найти их на канале) мы осветили тему строения атома, причём ровно в таком объёме, какой позволит нам без труда понять абсолютно все базовые химические закономерности.
Следующей супер важной темой на нашем пути станет тема атомного радиуса, именно она призвана внести в наше сознание понимание того, почему те или иные атомы ведут себя так, а не иначе при образовании более сложных соединений. Кроме того, атомный радиус – это первое понятие, которое раскроет перед нами ценность Периодической системы химических элементов Менделеева, обо всё этом ниже!
Если в математике радиус – это расстояние от центра до границы окружности, то в химии центром будет ядро, а границей окружности – электроны на внешнем энергетическом уровне.
Итак
* Атомный радиус – это условная величина, характеризующая удалённость электронов на внешнем энергетическом уровне от ядра. (условная, т.к. мы не будем использовать никаких единиц измерения).
Почему это важно? Вспоминайте, мы уже говорили с Вами, что именно электроны участвуют в образовании химической связи, причем чаще всего это электроны именно внешнего энергетического уровня, и такие электроны мы будем называть валентными.
А теперь попробуем понять следующую мысль: почему систему Менделеева называют периодической? Дело в том, что химические свойства атомов химических элементов изменяются совершенно определённым (периодическим) образом.
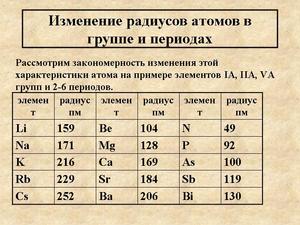
Чтобы прочувствовать этот момент обратимся к самой таблице: у нас есть периоды и группы, попробуем сравнить атомные радиусы двух соседних по подгруппе элементов – натрия Na и калия K.
Для этого рассмотрим их электронные формулы:
Довольно очевидно, что электроны на внешнем – четвёртом! – энергетическом уровне атома калия K более удалены от ядра, чем электроны на внешнем – третьем – энергетическом уровне атома натрия Na. Это значит, что атомный радиус К больше, чем атомный радиус Na, что мы можем обозначить следующим образом: r(Na) < r(K). Казалось бы, что из этого вытекает? Но! Так как данные атомы являются соседями по главной подгруппе первой группы, то из данного конкретного примера мы можем выделить закономерность изменения атомного радиуса в рамках любой подгруппы во всей таблице Менделеева!
Действуем! Атомный радиус возрастает от одного соседа по подгруппе Na к другому соседу K (сверху вниз), значит:
В переделах подгруппы в ПСХЭ (периодической системе химических элементов), сверху вниз, атомный радиус возрастает!
это довольно просто понять, учитывая, что в пределах одной подгруппы увеличивается номер периода каждого элемента, то есть увеличивается число энергетических уровней, соответственно электроны на внешнем энергетическом уровне оказываются всё более удалены от ядра.
Эта закономерность уже совсем скоро обозначит нам своё влияние на химические свойства атомов данных химических, а пока мы продолжаем:
А как быть в следующем случае: попробуем рассмотреть изменение атомного радиуса в пределах периода, для этого рассмотрим соседей по периоду: атомы Na и Mg:
Нам понадобятся их электронные формулы:
Число энергетических уровней у данных атомов одинаково, и разница в атомных радиусах уже не столь очевидна, верно? Вы можете даже подумать, что атомные радиусы данных атомов одинаковы, но это не так! Чтобы это понять, давайте подумаем, какие силы действуют между положительно заряженным ядром и отрицательно заряженными электронами, как между разноимённо заряженными частицами? Конечно! Силы притяжения. Вспоминаем закон Кулона: разноимённо заряженные частицы притягиваются, причём сила их взаимного притяжения прямо пропорциональна зарядам этих частиц и обратно пропорциональна расстоянию между ними. То есть, чем выше заряд ядра, тем сильнее оно притягивает электроны! Возвращаемся к нашему примеру – заряд ядра Na равен +11, а заряд ядра Mg = +12, значит, ядро атома Mg по сравнению с ядром атома Na сильнее тянет на себя электроны, как итог по сравнению с атомом Na, атом Mg как бы сжимается, и мы получаем, что
r (Na) > r (Mg) (если необходимо, вернитесь к ходу моих мыслей).
То есть, атомный радиус натрия оказывается больше, чем атомный радиус магния. Отсюда можем сделать вывод: если от одного соседа по третьему периоду, атома Na, к другому соседу по третьему периоду, атому Mg, (слева направо) атомный радиус уменьшается, значит можно сформулировать новую закономерность:
* в пределах любого периода (слева направо) атомный радиус будет уменьшаться!
Эта закономерность тоже уже очень скоро найдёт отражение в рассматриваемых нами химических свойствах, а пока подведём итог:
На этом наш текущий разговор подходит к концу.
В следующей серии мы выясним, какими интересами руководствуются атомы, образуя химические связи, и какую роль при этом играет атомный радиус.
А чтобы работать в этом направлении, следить за развитием нашей химической мысли, предлагаю подписаться на канал. Спасибо.