Биномиальный коэффициент — коэффициент перед членом разложения бинома Ньютона 








для натуральных степеней 
Биномиальные коэффициенты могут быть также определены для произвольных действительных показателей 


,
где в случае неотрицательных целых 


В комбинаторике биномиальный коэффициент 






Биномиальные коэффициенты часто возникают в задачах комбинаторики и теории вероятностей. Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.
Явные формулы[править | править код]
Вычисляя коэффициенты в разложении 

Для всех действительных чисел 

,
где 

Для неотрицательных целых 

.
Для целых отрицательных показателей коэффициенты разложения бинома 
.
Треугольник Паскаля[править | править код]


Визуализация биномиального коэффициента до 4 степени
Тождество:
позволяет расположить биномиальные коэффициенты для неотрицательных целых чисел 

.
Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от той, что выписана здесь, поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, Омару Хайяму).
Если в каждой строке треугольника Паскаля все числа разделить на 

Свойства[править | править код]
Производящие функции[править | править код]
Для фиксированного значения 

.
Для фиксированного значения 

.
Двумерной производящей функцией биномиальных коэффициентов 

, или
.
Делимость[править | править код]
Из теоремы Люка следует, что:
Основные тождества[править | править код]
.
.
(правило симметрии).
(вынесение за скобки).
(замена индексов).
.
Бином Ньютона и следствия[править | править код]
а более общем виде
.
Свёртка Вандермонда и следствия[править | править код]
Свёртка Вандермонда:
,
где 








Следствие свёртки Вандермонда:
.
Более общее тождество:
, если
.
Ещё одним следствием свёртки является следующее тождество:

Другие тождества[править | править код]
.
Также имеют место равенства:
Откуда следует:
,
где 


Матричные соотношения[править | править код]
Если взять квадратную матрицу, отсчитав 

В матрице 


,
где 

.
Таким образом, можно разложить обратную матрицу к 
, где
,
,
,
.
Элементы обратной матрицы меняются при изменении её размера и, в отличие от матрицы 







при
, где
многочлен степени
.
Если произвольный вектор длины 



Используя тождество выше и равенство единицы скалярного произведения нижней строки матрицы 

.
Для показателя большего 
,
где многочлен
.
Для доказательства сперва устанавливается тождество:
.
Если требуется найти формулу не для всех показателей степени, то:
.
Старший коэффициент 
для
.
Асимптотика и оценки[править | править код]
Непосредственно из формулы Стирлинга следует, что для 

Целозначные полиномы[править | править код]
Биномиальные коэффициенты 


В то же время стандартный базис 


Этот результат обобщается на полиномы многих переменных. А именно, если полином 

,
где 
Алгоритмы вычисления[править | править код]
Биномиальные коэффициенты можно вычислить с помощью рекуррентной формулы 










При фиксированном значении 





Если требуется вычислить коэффициенты 










Примечания[править | править код]
- ↑ Прасолов В. В. Глава 12. Целозначные многочлены // Многочлены. — М.: МЦНМО, 1999, 2001, 2003. Архивная копия от 21 января 2022 на Wayback Machine
- ↑ Ю. Матиясевич. Десятая проблема Гильберта. — Наука, 1993.
Литература[править | править код]
- Биномиальные коэффициенты // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17—25.
- Кузьмин О. В. Треугольник и пирамида Паскаля: свойства и обобщения // Соросовский Образовательный Журнал. — 2000. — Т. 6, № 5. — С. 101—109.
- Ландо С. К. Теневое исчисление // VIII летняя школа «Современная математика». — Дубна, 2008.
- Винберг Э. Б. Удивительные арифметические свойства биномиальных коэффициентов // Математическое просвещение. — 2008. — Вып. 12. — С. 33–42.
- Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Математические основы информатики = Concrete Mathematics. A Foundation for Computer Science. — 2-е. — М.: Мир; Бином. Лаборатория знаний; «Вильямс», 1998—2009. — 703, 784 с. — ISBN 95-94774-560-7, 78-5-8459-1588-7.
Бином Ньютона – формула
С натуральным n формула Бинома Ньютона принимает вид a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn, где имеем, что Cnk=(n)!(k)!·(n-k)!=n(n-1)·(n-2)·…·(n-(k-1))(k)!- биномиальные коэффициенты, где есть n по k, k=0,1,2,…,n, а “!” является знаком факториала.
В формуле сокращенного умножения a+b2=C20·a2+C21·a1·b+C22·b2=a2+2ab+b2
просматривается формула бинома Ньютона, так как при n=2 является его частным случаем.
Первая часть бинома называют разложением (a+b)n, а Сnk·an-k·bk – (k+1)-ым членом разложения, где k=0,1,2, …,n.
Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля
Представление биномиальных коэффициентов для различных n осуществляется при помощи таблицы, которая имеет название арифметического треугольника Паскаля. Общий вид таблицы:
| Показатель степени | Биноминальные коэффициенты | ||||||||||
| 0 | C00 | ||||||||||
| 1 | C10 | C11 | |||||||||
| 2 | C20 | C21 | C22 | ||||||||
| 3 | C30 | C31 | C32 | C33 | |||||||
| ⋮ | … | … | … | … | … | … | … | … | … | ||
| n | Cn0 | Cn1 | … | … | … | … | … | Cnn-1 | Cnn |
При натуральных n такой треугольник Паскаля состоит из значений коэффициентов бинома:
| Показатель степени | Биноминальные коэффициенты | ||||||||||||||
| 0 | 1 | ||||||||||||||
| 1 | 1 | 1 | |||||||||||||
| 2 | 1 | 2 | 1 | ||||||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| ⋮ | … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| n | Cn0 | Cn1 | … | … | … | … | … | … | … | … | … | Cnn-1 | Cnn |
Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.
Доказательство формулы бинома Ньютона
Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:
- коэффициента располагаются равноудалено от начала и конца, причем равны, что видно по формуле Cnp=Cnn-p, где р=0, 1, 2, …, n;
- Cnp=Cnp+1=Cn+1p+1;
- биномиальные коэффициенты в сумме дают 2 в степени показателя степени бинома, то есть Cn0+Cn1+Cn2+…+Cnn=2n;
- при четном расположении биноминальных коэффициентов их сумма равняется сумме биномиальных коэффициентов, расположенных в нечетных местах.
Равенство вида a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn считается справедливым. Докажем его существование.
Для этого необходимо применить метод математической индукции.
Для доказательства необходимо выполнить несколько пунктов:
- Проверка справедливости разложения при n=3. Имеем, что
a+b3=a+ba+ba+b=a2+ab+ba+b2a+b==a2+2ab+b2a+b=a3+2a2b+ab2+a2b+2ab+b3==a3+3a2b+3ab2+b3=C30a3+C31a2b+C32ab2+C33b3 - Если неравенство верно при n-1, тогда выражение вида a+bn-1=Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1
считается справедливым.
- Доказательство равенства a+bn-1=Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1, основываясь на 2 пункте.
Выражению
a+bn=a+ba+bn-1==(a+b)Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1
Необходимо раскрыть скобки, тогда получимa+bn=Cn-10·an+Cn-11·an-1·b+Cn-12·an-2·b2+…+Cn-1n-2·a2·bn-2++Cn-1n-1·a·bn-1+Cn-10·an-1·b+Cn-11·an-2·b2+Cn-12·an-3·b3+…+Cn-1n-2·a·bn-1+Cn-1n-1·bn
Производим группировку слагаемых
a+bn==Cn-10·an+Cn-11+Cn-10·an-1·b+Cn-12+Cn-11·an-2·b2+…++Cn-1n-1+Cn-1n-2·a·bn-1+Cn-1n-1·bn
Имеем, что Cn-10=1 и Cn0=1, тогда Cn-10=Cn0. Если Cn-1n-1=1 и Cnn=1, тогда Cn-1n-1=Cnn. При применении свойства сочетаний Cnp+Cnp+1=Cn+1p+1, получаем выражение вида
Cn-11+Cn-10=Cn1Cn-12+Cn-11=Cn2⋮Cn-1n-1+Cn-1n-2=Cnn-1
Произведем подстановку в полученное равенство. Получим, что
a+bn==Cn-10·an+Cn-11+Cn-10·an-1·b+Cn-12+Cn-11·an-2·b2+…++Cn-1n-1+Cn-1n-2·a·bn-1=Cn-1n-1·bn
После чего можно переходить к биному Ньютона, тогда a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn.
Формула бинома доказана.
Бином Ньютона – применение при решении примеров и задач
Для полного понятия использования формулы рассмотрим примеры.
Разложить выражение (a+b)5 , используя формулу бинома Ньютона.
Решение
По треугольнику Паскаля с пятой степенью видно, что биноминальные коэффициенты – это 1, 5, 10, 10, 5, 1. То есть, получаем, что a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 является искомым разложением.
Ответ: a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
Найти коэффициенты бинома Ньютона для шестого члена разложения выражения вида a+b10.
Решение
По условию имеем, что n=10, k=6-1=5. Тогда можно перейти к вычислению биномиального коэффициента:
Cnk=C105=(10)!(5)!·10-5!=(10)!(5)!·(5)!==10·9·8·7·6(5)!=10·9·8·7·61·2·3·4·5=252
Ответ: Cnk=C105=252
Ниже приведен пример, где используется бином для доказательства делимости выражения с заданным числом.
Доказать, что значение выражения 5n+28·n-1, при n, являющимся натуральным числом, делится на 16 без остатка.
Решение
Необходимо представить выражение в виде 5n=4+1n и воспользоваться биномом Ньютона. Тогда получим, что
5n+28·n-1=4+1n+28·n-1==Cn0·4n+Cn1·4n-1·1+…+Cnn-2·42·1n-2+Cnn-1·4·1n-1+Cnn·1n+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+n·4+1+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+32·n==16·(4n-2+Cn1·4n-3+…+Cnn-2+2·n)
Ответ: Исходя из полученного выражения, видно, что исходное выражение делится на 16.
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Бином Ньютона и треугольник Паскаля
18 декабря 2021
Сегодня мы детально разберём Бином Ньютона. Это формула, по которой можно раскрыть скобки ${{left( a+b right)}^{n}}$ и получить готовый многочлен. Сама формула выглядит так:
[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]
где $C_{n}^{k}$ — биноминальные коэффициенты (они же — «число сочетаний из $n$ по $k$»), которые считаются по формуле
[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]
Вот и всё. На этом можно было бы закончить, но есть одно но: большинство начинающих учеников не понимают эту формулу, не умеют пользоваться её, а уж чтобы доказать её — об этом даже речи не идёт.
Сегодня мы всё это исправим. Вы узнаете буквально всё, что нужно знать про Бином Ньютона:
- Постановка задачи — в чём вообще проблема?
- Формула бинома Ньютона — что значат все эти значки?
- Знак суммы — чрезвычайно полезный материал для всех, кто хочет понять математику.
- Биноминальные коэффициенты — минутка комбинаторики.
- Треугольник Паскаля — лайфхак для быстрых вычислений.
- Доказательство Бинома Ньютона — для тех, кто хочет познать Истину.:)
Материала много, но всё будет максимально понятно и — главное — чрезвычайно полезно. Погнали!
1. Постановка задачи
Итак, мы хотим быстро раскрывать скобки в конструкциях вида ${{left( a+b right)}^{n}}$. Начнём с того, что мы и так знаем. Например:
[{{left( a+b right)}^{1}}=a+b]
Спасибо, кэп. Теперь вспомним формулы сокращённого умножения. Квадрат суммы:
[{{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}]
И куб суммы:
[{{left( a+b right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}]
Видим, что с ростом степени растёт и количество слагаемых-одночленов: их всегда на одно больше, чем степень. Но это не проблема. Проблема в другом: у этих одночленов появляются некие коэффициенты, принцип вычисления которых не ясен. Пока не ясен…
Именно для нахождения этих коэффициентов придумали бином Ньютона.
2. Бином Ньютона
Пусть $nin mathbb{N}$. Тогда верно равенство
[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]
где $sum{left( … right)}$ — краткая запись суммы, $C_{n}^{k}$ — биноминальный коэффициент, который считается по формуле
[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]
В этой формуле прекрасно всё. Одних пугает знак суммы. Другие не понимают, что за $C_{n}^{k}$ такое (ещё раз: это объект из мира комбинаторики, читается «число сочетаний из $n$ по $k$»). Третьи более-менее понимают, о чём речь, но применить эту формулу на практике не могут.
Сегодня мы решим все эти проблемы. Начнём со знака суммы.
3. Знак суммы
Знак суммы — это краткая запись суммы нескольких однотипных слагаемых:
[sumlimits_{k=a}^{k=b}{fleft( k right)}]
Формула $fleft( k right)$ задаёт общий вид однотипных слагаемых, а нижний и верхний индексы $k=a$ и $k=b$ (сверху вместо $k=b$ обычно пишут просто $b$) определяют диапазон значений, которые «пробегает» $k$ и которые нужно подставить в $fleft( k right)$. Например:
[sumlimits_{k=3}^{5}{2k}=2cdot 3+2cdot 4+2cdot 5]
Более привычный формат:
[sumlimits_{k=1}^{n}{fleft( k right)=fleft( 1 right)+fleft( 2 right)+…+fleft( n right)}]
То же самое с индексами:
[sumlimits_{k=1}^{n}{{{a}_{k}}={{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}]
Обратите внимание: если $k$ пробегает значения от $k=a$ до $k=b$, то всего таких слагаемых будет ровно $b-a+1$:
[sumlimits_{k=a}^{b}{fleft( k right)=underbrace{fleft( a right)+fleft( a+1 right)+ldots +fleft( b right)}_{b-a+1text{ слагаемых!}}}]
Кроме того, полезно потренироваться и с обратным переходом — от полной записи к краткой:
[frac{1}{1}+frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}=sumlimits_{n=1}^{5}{frac{1}{2n-1}}]
[frac{2}{3}+frac{4}{9}+frac{6}{27}+frac{8}{81}=sumlimits_{n=1}^{4}{frac{2n}{{{3}^{n}}}}]
В приложении к уроку — куча задач для самостоятельной тренировки.
Но вернёмся к биному Ньютона. Распишем его без знака суммы:
[begin{align} {{left( a+b right)}^{n}} & =C_{n}^{0}cdot {{a}^{n}}{{b}^{0}}+C_{n}^{1}cdot {{a}^{n-1}}{{b}^{1}}+ \ & +ldots +C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}+ldots + \ & +C_{n}^{n-1}cdot {{a}^{1}}{{b}^{n-1}}+C_{n}^{n}cdot {{a}^{0}}{{b}^{n}} end{align}]
В целом, всё понятно: степени буквы $a$ уменьшаются с ${{a}^{n}}$ до ${{a}^{0}}$; одновременно степени буквы $b$ растут с ${{b}^{0}}$ до ${{b}^{n}}$. Сумма степеней этих букв в каждом одночлене равна $n$. Но что такое $C_{n}^{k}$?
4. Биноминальные коэффициенты
Немного комбинаторики.
Определение. Число сочетаний из $n$ по $k$ — это число способов, которыми можно выбрать $k$ элементов среди $n$ элементов, если порядок выбора не имеет значения. Обозначается $C_{n}^{k}$ и считается по формуле
[C_{n}^{k}=frac{n!}{k!left( n-k right)!}]
Обратите внимание: в числителе и знаменателе стоят факториалы. Стандартное определение: $n!$ — это произведение всех чисел от единицы до $n$:
[n!=1cdot 2cdot 3cdot …cdot n]
У факториалов много интересных свойств. Чуть позже мы рассмотрим их и даже введём более корректное определение самого факториала. А пока просто потренируемся считать биноминальные коэффициенты.
Пример. На пруду плавают 5 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?
Очевидно, порядок кормления уток неважен. Покормить сначала утку №1, а затем №2 — это то же самое, что покормить сначала утку №2, затем №1. Результат один и тот же: накормлены лишь эти две утки, а остальные три — нет. Поэтому считаем $C_{5}^{2}$:
[begin{align} C_{5}^{2} & =frac{5!}{2!cdot 3!} \ & =frac{5cdot 4cdot 3cdot 2cdot 1}{2cdot 1cdot 3cdot 2cdot 1}= \ & =10 end{align}]
Вот и всё. Однако при больших $n$ и $k$ посчитать число сочетаний напрямую становится затруднительно. Тут на помощь приходит сокращение дробей.
Пример. На пруду 150 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?
Порядок вновь неважен, просто уток стало больше. Поэтому считаем $C_{150}^{2}$:
[begin{align} C_{150}^{2} & =frac{150!}{2!cdot 148!}= \ & =frac{150cdot 149cdot 148cdot …cdot 1}{2cdot 1cdot 148cdot …cdot 1}= \ & =frac{150cdot 149}{2cdot 1}= \ & =11175 end{align}]
Видим, что факториалы образуют «длинные хвосты» в числителе и знаменателе, которые легко сокращаются. Однако для корректной работы с биномом Ньютона нам потребуется расширить определение факториала.
4.1. Новое определение факториала
Стандартное определение мы уже привели выше:
[n!=1cdot 2cdot 3cdot …cdot n,quad nin mathbb{N}]
Но как посчитать, например, факториал нуля? И как сокращать «длинные хвосты», не расписывая факториалы? Здесь нам поможет более грамотное определение.
Определение. Пусть $nin mathbb{N}bigcup left{ 0 right}$ — целое неотрицательное число. Тогда факториал считается по формуле:
[n!=left{ begin{align} & 1,quad n=0 \ & ncdot left( n-1 right)!,quad n gt 0 \ end{align} right.]
В частности, $0!=1$ по определению.
Простейшие коэффициенты:
[begin{align} C_{n}^{0} & =frac{n!}{0!left( n-0 right)!}=frac{n!}{1cdot n!}=1; \ C_{n}^{1} & =frac{n!}{1!left( n-1 right)!}=frac{ncdot left( n-1 right)!}{1cdot left( n-1 right)!}=n; \ end{align}]
А вот ещё парочка весёлых примеров:
[begin{align} C_{7}^{3} & =frac{7cdot 6cdot 5cdot 4cdot ldots cdot 1}{3cdot 2cdot 1cdot 4cdot ldots cdot 1}=35 \ C_{8}^{2} & =frac{8cdot 7cdot 6cdot ldots cdot 1}{2cdot 1cdot 6cdot ldots cdot 1}=28 \ C_{64}^{3} & =frac{64cdot 63cdot 62cdot 61cdot ldots cdot 1}{3cdot 2cdot 1cdot 61cdot ldots cdot 1}= \ & =41664 end{align}]
5. Треугольник Паскаля
Посчитаем бином Ньютона для $n=0$, $n=1$, $n=2$, $n=3$:
[begin{align} & {{left( a+b right)}^{0}}=1 \ & {{left( a+b right)}^{1}}=1cdot a+1cdot b \ & {{left( a+b right)}^{2}}=1cdot {{a}^{2}}+2cdot ab+1cdot {{b}^{2}} \ & {{left( a+b right)}^{3}}=1cdot {{a}^{3}}+3cdot {{a}^{2}}b+3cdot a{{b}^{2}}+1cdot {{b}^{3}} \ end{align}]
Составим таблицу:
[begin{matrix} 1 \ 1quad 1 \ 1quad 2quad 1 \ 1quad 3quad 3quad 1 \ 1quad 4quad 6quad 4quad 1 \ end{matrix}]
Получили треугольник, который в народе называют «Треугольник Паскаля»: по бокам единицы, а внутри каждое число равно сумме двух ближайших, стоящих этажом выше:
[begin{align} & 3=1+2 \ & 4=1+3 \ & 6=3+3 \ end{align}]
И это не случайность. Перед нами важнейшее свойство биноминальных коэффициентов, которое мы оформим в виде теоремы и докажем.
Теорема. Биноминальные коэффициенты вычисляются по формуле
[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]
Доказывается напролом.
Распишем доказательство детально:
[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!}]
[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{n!}{k!left( n-k right)!}+frac{n!}{left( k+1 right)!left( n-k-1 right)!} \ end{align}]
Заметим, что по определению факториала
[begin{align} & left( k+1 right)!=left( k+1 right)cdot k! \ & left( n-k right)!=left( n-k right)cdot left( n-k-1 right)! end{align}]
Поэтому знаменатели биноминальных коэффициентов можно переписать:
[C_{n}^{k}+C_{n}^{k+1}=frac{n!}{k!left( n-k right)left( n-k-1 right)!}+frac{n!}{left( k+1 right)k!left( n-k-1 right)!}]
[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{n!}{k!left( n-k right)left( n-k-1 right)!}+ \ & +frac{n!}{left( k+1 right)k!left( n-k-1 right)!} end{align}]
Приведём к общему знаменателю:
[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} end{align}]
[begin{align} & C_{n}^{k}+C_{n}^{k+1}= \ = & frac{left( k+1 right)cdot n!}{left( k+1 right)!left( n-k right)!}+frac{left( n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}= \ = & frac{left( k+1+n-k right)cdot n!}{left( k+1 right)!left( n-k right)!}=frac{left( n+1 right)cdot n!}{left( k+1 right)!left( n-k right)!} \ end{align}]
Окончательно получим:
[begin{align} C_{n}^{k}+C_{n}^{k+1} & =frac{left( n+1 right)!}{left( k+1 right)!left( n-k right)!}= \ & =frac{left( n+1 right)!}{left( k+1 right)!left( n+1-left( k+1 right) right)!}= \ & = C_{n+1}^{k+1} end{align}]
Теорема доказана. Теперь мы знаем, как формируется треугольник Паскаля. Осталось доказать сам Бином Ньютона.
6. Доказательство Бинома Ньютона
Итак, нужно доказать, что
[{{left( a+b right)}^{n}}=sumlimits_{k=0}^{n}{C_{n}^{k}cdot {{a}^{n-k}}{{b}^{k}}}]
где $C_{n}^{k}$ — биноминальные коэффициенты с теми чудесными свойствами, которые мы рассмотрели и доказали выше.
Будем доказывать по индукции.
6.1. База индукции
Рассмотрим $n=1$. Формула Бинома Ньютона для него:
[begin{align} {{left( a+b right)}^{1}} & =sumlimits_{k=0}^{1}{C_{1}^{k}{{a}^{1-k}}{{b}^{k}}}= \ & =C_{1}^{0}{{a}^{1}}{{b}^{0}}+C_{1}^{1}{{a}^{0}}{{b}^{1}}= \ & =a+bend{align}]
Очевидно, для $n=1$ формула верна. Переходим к индуктивному предположению.
6.2. Индуктивное предположение
Пусть Бином Ньютона верен для некоторого $n=t$:
[{{left( a+b right)}^{t}}=sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}]
Используя этот факт, докажем верность и для $n=t+1$, т.е. выполним индуктивный переход.
6.3. Индуктивный переход
Докажем, что бином Ньютона верен для $n=t+1$:
[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]
Для этого сначала заметим, что
[{{left( a+b right)}^{t+1}}={{left( a+b right)}^{t}}cdot left( a+b right)]
Однако согласно индуктивному предположению, ${{left( a+b right)}^{t}}$ допускает разложение по Биному Ньютона, поэтому
[begin{align} left( a+b right)cdot {{left( a+b right)}^{t}} & =left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ & =sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} end{align}]
[begin{align} & left( a+b right)cdot {{left( a+b right)}^{t}}= \ = & left( a+b right)cdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & acdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}+bcdot sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k}}}= \ = & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} \ end{align}]
Запишем отдельно первое слагаемое первой суммы и учтём, что $C_{t}^{0}=C_{t+1}^{0}=1$:
[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} & = C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ & = C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} end{align}]
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}= \ = & C_{t}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]
И последнее слагаемое последней второй суммы и учтём, что $C_{t}^{t}=C_{t+1}^{t+1}=1$:
[begin{align} sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}} & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ & =sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} end{align}]
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t}^{t}cdot {{b}^{t+1}} \ = & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Сейчас будет самая нетривиальная операция. Меняем индекс суммирования в последней сумме: выполняем подстановку $k=m-1$. При этом меняются и пределы суммирования:
[left[ begin{align} k & =m-1 \ k & =0Rightarrow m=1 \ k & =t-1Rightarrow m=t \ k+1 & =m \ t-k & =t+1-m \ end{align} right]]
В итоге последняя сумма перепишется так:
[sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]
[begin{align} & sumlimits_{k=0}^{t-1}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ = & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Объединяем суммы вместе:
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
[begin{align} & sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+sumlimits_{k=0}^{t}{C_{t}^{k}cdot {{a}^{t-k}}{{b}^{k+1}}}= \ = & C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+ \ + & sumlimits_{m=1}^{t}{C_{t}^{m-1}cdot {{a}^{t+1-m}}{{b}^{m}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Заметим, что два знака суммы различаются лишь названием индекса и биноминальными коэффициентами. Всё остальное — диапазоны суммирования, степени буквы $a$ и буквы $b$ — всё идеально совпадает и никак не меняется, если написать вместо $k$ индекс $m$ или наоборот.
Такие суммы можно записать под единым знаком:
[C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+C_{t+1}^{t+1}cdot {{b}^{t+1}}]
[begin{align} & C_{t+1}^{0}cdot {{a}^{t+1}}+ \ + & sumlimits_{k=1}^{t}{left( C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} right)}+ \ + & C_{t+1}^{t+1}cdot {{b}^{t+1}} \ end{align}]
Выражение под знаком суммы легко раскладывается на множители:
[begin{align} C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}} & =left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ & =C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} end{align}]
[begin{align} & C_{t}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}+C_{t}^{k-1}cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & left( C_{t}^{k}+C_{t}^{k-1} right)cdot {{a}^{t+1-k}}{{b}^{k}}= \ = & C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}} \ end{align}]
Здесь в последнем шаге мы использовали свойство биноминальных коэффициентов, доказанное выше:
[C_{n}^{k}+C_{n}^{k+1}=C_{n+1}^{k+1}]
Или, что то же самое
[C_{n}^{k-1}+C_{n}^{k}=C_{n+1}^{k}]
Таким образом, всю сумму можно переписать более компактно, а затем внести под знак суммы первое и последнее слагаемое:
[ C_{t+1}^{0}cdot {{a}^{t+1}}+sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]
[begin{align} C_{t+1}^{0}cdot {{a}^{t+1}} & +sumlimits_{k=1}^{t}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}+C_{t+1}^{t+1}cdot {{b}^{t+1}}= \ & =sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}} \ end{align}]
Сопоставляя исходное выражение и конечное, получим
[{{left( a+b right)}^{t+1}}=sumlimits_{k=0}^{t+1}{C_{t+1}^{k}cdot {{a}^{t+1-k}}{{b}^{k}}}]
Именно это и требовалось доказать. Следовательно, исходная формула Бинома Ньютона верна.
Смотрите также:
- Схема Горнера

- Теорема Безу и корни многочленов

- Знаки тригонометрических функций

- Уравнение касательной к графику функции

- Как представить обычную дробь в виде десятичной

- Сложные задачи B2 на проценты: вычисление полной стоимости

Биномиальные коэффициенты
- Биномиальные коэффициенты
-
Биномиальные коэффициенты — коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона):
Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов.
Значение биномиального коэффициента
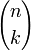 определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов:
определено для всех целых чисел n и k. Явные формулы для вычисления биномиальных коэффициентов: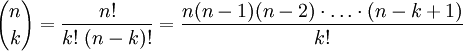 для
для 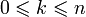 ;
;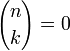 для k < 0 или
для k < 0 или 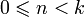 ;
;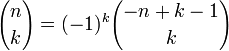 для
для 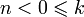 ,
,
где n! и k! — факториалы чисел n и k.
Биномиальный коэффициент
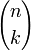 является обобщением числа сочетаний
является обобщением числа сочетаний 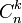 , которое определено только для неотрицательных целых чисел n, k.
, которое определено только для неотрицательных целых чисел n, k.Биномиальные коэффициенты часто возникают в комбинаторных задачах и теории вероятностей.
Обобщением биномиальных коэффициентов являются мультиномиальные коэффициенты.
Содержание
- 1 Треугольник Паскаля
- 2 Свойства
- 3 Тождества
- 4 Асимптотика и оценки
- 5 Алгоритмы вычисления биномиальных коэффициентов
- 6 См. также
- 7 Ссылки
Треугольник Паскаля

Тождество
позволяет расположить биномиальные коэффициенты для неотрицательных n, k в виде треугольника Паскаля, в котором каждое число равно сумме двух вышестоящих:
Треугольная таблица, предложенная Паскалем в «Трактате об арифметическом треугольнике» (1654), отличается от выписанной здесь поворотом на 45°. Таблицы для изображения биномиальных коэффициентов были известны и ранее (Тарталье, О. Хайяму и др.).
Свойства
Интересно, что если рассмотреть ряды в треугольнике Паскаля, состоящие из биномиальных коэффициентов, то в пределе получим функцию нормального распределения — распределение Гаусса.
Из теоремы Люка следует, что:
Тождества
Асимптотика и оценки
Алгоритмы вычисления биномиальных коэффициентов
Биномиальные коэффициенты могут быть вычислены с помощью формулы
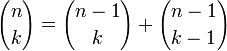 , если на каждом шаге хранить значения
, если на каждом шаге хранить значения 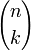 при
при 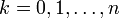 . Этот алгоритм особенно эффективен, если нужно получить все значения
. Этот алгоритм особенно эффективен, если нужно получить все значения 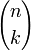 при фиксированном n. Алгоритм требует O(n) памяти (O(n2) при вычислении всей таблицы биномиальных коэффициентов) и O(n2) времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).
при фиксированном n. Алгоритм требует O(n) памяти (O(n2) при вычислении всей таблицы биномиальных коэффициентов) и O(n2) времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).Второй способ основан на тождестве
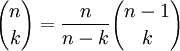 . Он позволяет вычислить значения
. Он позволяет вычислить значения 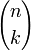 при фиксированном k. Алгоритм требует O(1) памяти (O(l) если нужно посчитать l последовательных коэффициентов с фиксированным k) и O(k) времени.
при фиксированном k. Алгоритм требует O(1) памяти (O(l) если нужно посчитать l последовательных коэффициентов с фиксированным k) и O(k) времени.См. также
- Биномиальное распределение
- Треугольное число
- Треугольник Паскаля
- Пирамида Паскаля
- Композиция (теория чисел)
- Разбиение числа
Ссылки
- О. В. Кузьмин Треугольник и пирамида Паскаля: свойства и обобщения // Соросовский Образовательный Журнал. — 2000. — Т. 6. — № 5. — С. 101—109.
- С. К. Абачиев Радужная фрактальность треугольника Паскаля
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое “Биномиальные коэффициенты” в других словарях:
-
Биномиальные коэффициенты — коэффициенты в формуле разложения Ньютона бинома … Большая советская энциклопедия
-
БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ — коэффициенты при степенях z в разложений Ньютона бинома . Б. к. обозначается или и равен Обозначение восходит к Л. Эйлеру (L. Euler); второе обозначение появилось в 19 в. и связано, по видимому, с интерпретацией Б. к. как числа различимых… … Математическая энциклопедия
-
Биномиальные коэффициенты — так называются количества: l, n/1, n(n 1)/(1.2), n(n 1)(n 2)/(1.2.3)…, n(n 1)(n 2)…(n m + 1)/(1.2.3…m), составляющие коэффициенты последовательных членов бинома Ньютона (см. Бином). Их обозначают в настоящее время часто знаком . Общий вид Б … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
-
Паскаля треугольник — Биномиальные коэффициенты коэффициенты в разложении (1 + x)n по степеням x (т. н. бином Ньютона): Иначе говоря, (1 + x)n является производящей функцией для биномиальных коэффициентов. Значение биномиального коэффициента определено для всех целых… … Википедия
-
Биномиальный коэффициент — В математике биномиальные коэффициенты это коэффициенты в разложении бинома Ньютона по степеням x. Коэффициент при обозначается или и читается «биномиальный коэффициент из n по k» (или «це из n по k»): В … Википедия
-
Ньютона бином — название формулы, выражающей любую целую положительную степень суммы двух слагаемых (бинома, двучлена) через степени этих слагаемых, а именно: (1) (1) где n целое положительное число, а и b какие угодно числа.… … Большая советская энциклопедия
-
Бином Ньютона — Бином Ньютона формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид , где биномиальные коэффициенты, неотрицательное целое число. В таком виде эта формула была известна… … Википедия
-
биномиальное распределение — (распределение Бернулли), распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях, если вероятность появления этого события в каждом испытании равна р (0≤р≤1). Именно, число μ появлений этого события… … Энциклопедический словарь
-
Последовательность Падована — Последовательность Падована это целочисленная последовательность P(n) с начальными значениями и линейным рекуррентным соотношением Первые значения P(n) таковы 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 … Википедия
-
Бином ньютона — Бином Ньютона это формула , где биномиальные коэффициенты, n неотрицательное целое число. Содержание 1 Доказательство … Википедия

The binomial coefficients can be arranged to form Pascal’s triangle, in which each entry is the sum of the two immediately above.

Visualisation of binomial expansion up to the 4th power
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written 
which using factorial notation can be compactly expressed as
For example, the fourth power of 1 + x is
and the binomial coefficient 
Arranging the numbers 

The binomial coefficients occur in many areas of mathematics, and especially in combinatorics. The symbol 





The binomial coefficients can be generalized to 
History and notation[edit]
Andreas von Ettingshausen introduced the notation 
Alternative notations include C(n, k), nCk, nCk, Ckn, Cnk, and Cn,k in all of which the C stands for combinations or choices. Many calculators use variants of the C notation because they can represent it on a single-line display. In this form the binomial coefficients are easily compared to k-permutations of n, written as P(n, k), etc.
Definition and interpretations[edit]
|
k n |
0 | 1 | 2 | 3 | 4 | ⋯ |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | ⋯ |
| 1 | 1 | 1 | 0 | 0 | 0 | ⋯ |
| 2 | 1 | 2 | 1 | 0 | 0 | ⋯ |
| 3 | 1 | 3 | 3 | 1 | 0 | ⋯ |
| 4 | 1 | 4 | 6 | 4 | 1 | ⋯ |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋱ |
| The first few binomial coefficients on a left-aligned Pascal’s triangle |
For natural numbers (taken to include 0) n and k, the binomial coefficient 
-
(∗)
(valid for any elements x, y of a commutative ring),
which explains the name “binomial coefficient”.
Another occurrence of this number is in combinatorics, where it gives the number of ways, disregarding order, that k objects can be chosen from among n objects; more formally, the number of k-element subsets (or k-combinations) of an n-element set. This number can be seen as equal to the one of the first definition, independently of any of the formulas below to compute it: if in each of the n factors of the power (1 + X)n one temporarily labels the term X with an index i (running from 1 to n), then each subset of k indices gives after expansion a contribution Xk, and the coefficient of that monomial in the result will be the number of such subsets. This shows in particular that 



Computing the value of binomial coefficients[edit]
See also: § In programming languages
Several methods exist to compute the value of 
Recursive formula[edit]
One method uses the recursive, purely additive formula
for all integers 
with initial/boundary values
for all integers
The formula follows from considering the set {1, 2, 3, …, n} and counting separately (a) the k-element groupings that include a particular set element, say “i“, in every group (since “i” is already chosen to fill one spot in every group, we need only choose k − 1 from the remaining n − 1) and (b) all the k-groupings that don’t include “i“; this enumerates all the possible k-combinations of n elements. It also follows from tracing the contributions to Xk in (1 + X)n−1(1 + X). As there is zero Xn+1 or X−1 in (1 + X)n, one might extend the definition beyond the above boundaries to include 
Multiplicative formula[edit]
A more efficient method to compute individual binomial coefficients is given by the formula
where the numerator of the first fraction 
This formula is easiest to understand for the combinatorial interpretation of binomial coefficients.
The numerator gives the number of ways to select a sequence of k distinct objects, retaining the order of selection, from a set of n objects. The denominator counts the number of distinct sequences that define the same k-combination when order is disregarded.
Due to the symmetry of the binomial coefficient with regard to k and n − k, calculation may be optimised by setting the upper limit of the product above to the smaller of k and n − k.
Factorial formula[edit]
Finally, though computationally unsuitable, there is the compact form, often used in proofs and derivations, which makes repeated use of the familiar factorial function:
where n! denotes the factorial of n. This formula follows from the multiplicative formula above by multiplying numerator and denominator by (n − k)!; as a consequence it involves many factors common to numerator and denominator. It is less practical for explicit computation (in the case that k is small and n is large) unless common factors are first cancelled (in particular since factorial values grow very rapidly). The formula does exhibit a symmetry that is less evident from the multiplicative formula (though it is from the definitions)
-
(1)
which leads to a more efficient multiplicative computational routine. Using the falling factorial notation,
Generalization and connection to the binomial series[edit]
The multiplicative formula allows the definition of binomial coefficients to be extended[3] by replacing n by an arbitrary number α (negative, real, complex) or even an element of any commutative ring in which all positive integers are invertible:
With this definition one has a generalization of the binomial formula (with one of the variables set to 1), which justifies still calling the 
-
(2)
This formula is valid for all complex numbers α and X with |X| < 1. It can also be interpreted as an identity of formal power series in X, where it actually can serve as definition of arbitrary powers of power series with constant coefficient equal to 1; the point is that with this definition all identities hold that one expects for exponentiation, notably
If α is a nonnegative integer n, then all terms with k > n are zero, and the infinite series becomes a finite sum, thereby recovering the binomial formula. However, for other values of α, including negative integers and rational numbers, the series is really infinite.
Pascal’s triangle[edit]

1000th row of Pascal’s triangle, arranged vertically, with grey-scale representations of decimal digits of the coefficients, right-aligned. The left boundary of the image corresponds roughly to the graph of the logarithm of the binomial coefficients, and illustrates that they form a log-concave sequence.
Pascal’s rule is the important recurrence relation
-
(3)
which can be used to prove by mathematical induction that 
Pascal’s rule also gives rise to Pascal’s triangle:
| 0: | 1 | ||||||||||||||||
| 1: | 1 | 1 | |||||||||||||||
| 2: | 1 | 2 | 1 | ||||||||||||||
| 3: | 1 | 3 | 3 | 1 | |||||||||||||
| 4: | 1 | 4 | 6 | 4 | 1 | ||||||||||||
| 5: | 1 | 5 | 10 | 10 | 5 | 1 | |||||||||||
| 6: | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||||
| 7: | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||||
| 8: | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
Row number n contains the numbers 
Combinatorics and statistics[edit]
Binomial coefficients are of importance in combinatorics, because they provide ready formulas for certain frequent counting problems:
Binomial coefficients as polynomials[edit]
For any nonnegative integer k, the expression 
this presents a polynomial in t with rational coefficients.
As such, it can be evaluated at any real or complex number t to define binomial coefficients with such first arguments. These “generalized binomial coefficients” appear in Newton’s generalized binomial theorem.
For each k, the polynomial 
Its coefficients are expressible in terms of Stirling numbers of the first kind:
The derivative of 
This can cause a problem when evaluated at integers from 

Binomial coefficients as a basis for the space of polynomials[edit]
Over any field of characteristic 0 (that is, any field that contains the rational numbers), each polynomial p(t) of degree at most d is uniquely expressible as a linear combination 
-
(4)
Integer-valued polynomials[edit]
Each polynomial 

Example[edit]
The integer-valued polynomial 3t(3t + 1) / 2 can be rewritten as
Identities involving binomial coefficients[edit]
The factorial formula facilitates relating nearby binomial coefficients. For instance, if k is a positive integer and n is arbitrary, then
-
(5)
and, with a little more work,
We can also get
Moreover, the following may be useful:
For constant n, we have the following recurrence:
To sum up, we have
Sums of the binomial coefficients[edit]
The formula
-
(∗∗)
says the elements in the nth row of Pascal’s triangle always add up to 2 raised to the nth power. This is obtained from the binomial theorem (∗) by setting x = 1 and y = 1. The formula also has a natural combinatorial interpretation: the left side sums the number of subsets of {1, …, n} of sizes k = 0, 1, …, n, giving the total number of subsets. (That is, the left side counts the power set of {1, …, n}.) However, these subsets can also be generated by successively choosing or excluding each element 1, …, n; the n independent binary choices (bit-strings) allow a total of 
The formulas
-
(6)
and
follow from the binomial theorem after differentiating with respect to x (twice for the latter) and then substituting x = y = 1.
The Chu–Vandermonde identity, which holds for any complex values m and n and any non-negative integer k, is
-
(7)
and can be found by examination of the coefficient of 
Pascal’s triangle, rows 0 through 7. Equation 8 for m = 3 is illustrated in rows 3 and 6 as
-
(8)
where the term on the right side is a central binomial coefficient.
Another form of the Chu–Vandermonde identity, which applies for any integers j, k, and n satisfying 0 ≤ j ≤ k ≤ n, is
-
(9)
The proof is similar, but uses the binomial series expansion (2) with negative integer exponents.
When j = k, equation (9) gives the hockey-stick identity
and its relative
Let F(n) denote the n-th Fibonacci number.
Then
This can be proved by induction using (3) or by Zeckendorf’s representation. A combinatorial proof is given below.
Multisections of sums[edit]
For integers s and t such that 
For small s, these series have particularly nice forms; for example,[6]
Partial sums[edit]
Although there is no closed formula for partial sums
of binomial coefficients,[7] one can again use (3) and induction to show that for k = 0, …, n − 1,
with special case[8]
for n > 0. This latter result is also a special case of the result from the theory of finite differences that for any polynomial P(x) of degree less than n,[9]
Differentiating (2) k times and setting x = −1 yields this for

when 0 ≤ k < n,
and the general case follows by taking linear combinations of these.
When P(x) is of degree less than or equal to n,
-
(10)
where 
More generally for (10),
where m and d are complex numbers. This follows immediately applying (10) to the polynomial 


The series 

Identities with combinatorial proofs[edit]
Many identities involving binomial coefficients can be proved by combinatorial means. For example, for nonnegative integers 
(which reduces to (6) when q = 1) can be given a double counting proof, as follows. The left side counts the number of ways of selecting a subset of [n] = {1, 2, …, n} with at least q elements, and marking q elements among those selected. The right side counts the same thing, because there are 

In Pascal’s identity
both sides count the number of k-element subsets of [n]: the two terms on the right side group them into those that contain element n and those that do not.
The identity (8) also has a combinatorial proof. The identity reads
Suppose you have 


Now apply (1) to get the result.
If one denotes by F(i) the sequence of Fibonacci numbers, indexed so that F(0) = F(1) = 1, then the identity
has the following combinatorial proof.[10] One may show by induction that F(n) counts the number of ways that a n × 1 strip of squares may be covered by 2 × 1 and 1 × 1 tiles. On the other hand, if such a tiling uses exactly k of the 2 × 1 tiles, then it uses n − 2k of the 1 × 1 tiles, and so uses n − k tiles total. There are 
Sum of coefficients row[edit]
The number of k-combinations for all k, 

Dixon’s identity[edit]
Dixon’s identity is
or, more generally,
where a, b, and c are non-negative integers.
Continuous identities[edit]
Certain trigonometric integrals have values expressible in terms of binomial coefficients: For any 
These can be proved by using Euler’s formula to convert trigonometric functions to complex exponentials, expanding using the binomial theorem, and integrating term by term.
Congruences[edit]
If n is prime, then
for every k with
More generally, this remains true if n is any number and k is such that all the numbers between 1 and k are coprime to n.
Indeed, we have
Generating functions[edit]
Ordinary generating functions[edit]
For a fixed n, the ordinary generating function of the sequence 
For a fixed k, the ordinary generating function of the sequence 
The bivariate generating function of the binomial coefficients is
A symmetric bivariate generating function of the binomial coefficients is
which is the same as the previous generating function after the substitution 
Exponential generating function[edit]
A symmetric exponential bivariate generating function of the binomial coefficients is:
Divisibility properties[edit]
In 1852, Kummer proved that if m and n are nonnegative integers and p is a prime number, then the largest power of p dividing 
Equivalently, the exponent of a prime p in
equals the number of nonnegative integers j such that the fractional part of k/pj is greater than the fractional part of n/pj. It can be deduced from this that 


A somewhat surprising result by David Singmaster (1974) is that any integer divides almost all binomial coefficients. More precisely, fix an integer d and let f(N) denote the number of binomial coefficients 

Since the number of binomial coefficients 
Binomial coefficients have divisibility properties related to least common multiples of consecutive integers. For example:[11]




Another fact:
An integer n ≥ 2 is prime if and only if
all the intermediate binomial coefficients
are divisible by n.
Proof:
When p is prime, p divides
for all 0 < k < p
because 
When n is composite, let p be the smallest prime factor of n and let k = n/p. Then 0 < p < n and
otherwise the numerator k(n − 1)(n − 2)⋯(n − p + 1) has to be divisible by n = k×p, this can only be the case when (n − 1)(n − 2)⋯(n − p + 1) is divisible by p. But n is divisible by p, so p does not divide n − 1, n − 2, …, n − p + 1 and because p is prime, we know that p does not divide (n − 1)(n − 2)⋯(n − p + 1) and so the numerator cannot be divisible by n.
Bounds and asymptotic formulas[edit]
The following bounds for 
The first inequality follows from the fact that
and each of these 



From the divisibility properties we can infer that
where both equalities can be achieved.[11]
The following bounds are useful in information theory:[12]: 353
where 
for all 
Both n and k large[edit]
Stirling’s approximation yields the following approximation, valid when 
Because the inequality forms of Stirling’s formula also bound the factorials, slight variants on the above asymptotic approximation give exact bounds.
In particular, when 
and
and, more generally, for m ≥ 2 and n ≥ 1,[why?]
If n is large and k is linear in n, various precise asymptotic estimates exist for the binomial coefficient 

where d = n − 2k.[14]
n much larger than k[edit]
If n is large and k is o(n) (that is, if k/n → 0), then
where again o is the little o notation.[15]
Sums of binomial coefficients[edit]
A simple and rough upper bound for the sum of binomial coefficients can be obtained using the binomial theorem:
More precise bounds are given by
valid for all integers 

Generalized binomial coefficients[edit]
The infinite product formula for the gamma function also gives an expression for binomial coefficients
which yields the asymptotic formulas
as 
This asymptotic behaviour is contained in the approximation
as well. (Here 

Further, the asymptotic formula
hold true, whenever 


Generalizations[edit]
Generalization to multinomials[edit]
Binomial coefficients can be generalized to multinomial coefficients defined to be the number:
where
While the binomial coefficients represent the coefficients of (x+y)n, the multinomial coefficients
represent the coefficients of the polynomial
The case r = 2 gives binomial coefficients:
The combinatorial interpretation of multinomial coefficients is distribution of n distinguishable elements over r (distinguishable) containers, each containing exactly ki elements, where i is the index of the container.
Multinomial coefficients have many properties similar to those of binomial coefficients, for example the recurrence relation:
and symmetry:
where 
Taylor series[edit]
Using Stirling numbers of the first kind the series expansion around any arbitrarily chosen point 
Binomial coefficient with n = 1/2[edit]
The definition of the binomial coefficients can be extended to the case where 

In particular, the following identity holds for any non-negative integer 
This shows up when expanding 
Products of binomial coefficients[edit]
One can express the product of two binomial coefficients as a linear combination of binomial coefficients:
where the connection coefficients are multinomial coefficients. In terms of labelled combinatorial objects, the connection coefficients represent the number of ways to assign m + n − k labels to a pair of labelled combinatorial objects—of weight m and n respectively—that have had their first k labels identified, or glued together to get a new labelled combinatorial object of weight m + n − k. (That is, to separate the labels into three portions to apply to the glued part, the unglued part of the first object, and the unglued part of the second object.) In this regard, binomial coefficients are to exponential generating series what falling factorials are to ordinary generating series.
The product of all binomial coefficients in the nth row of the Pascal triangle is given by the formula:
Partial fraction decomposition[edit]
The partial fraction decomposition of the reciprocal is given by
Newton’s binomial series[edit]
Newton’s binomial series, named after Sir Isaac Newton, is a generalization of the binomial theorem to infinite series:
The identity can be obtained by showing that both sides satisfy the differential equation (1 + z) f’(z) = α f(z).
The radius of convergence of this series is 1. An alternative expression is
where the identity
is applied.
Multiset (rising) binomial coefficient[edit]
Binomial coefficients count subsets of prescribed size from a given set. A related combinatorial problem is to count multisets of prescribed size with elements drawn from a given set, that is, to count the number of ways to select a certain number of elements from a given set with the possibility of selecting the same element repeatedly. The resulting numbers are called multiset coefficients;[17] the number of ways to “multichoose” (i.e., choose with replacement) k items from an n element set is denoted 
To avoid ambiguity and confusion with n’s main denotation in this article,
let f = n = r + (k − 1) and r = f − (k − 1).
Multiset coefficients may be expressed in terms of binomial coefficients by the rule
One possible alternative characterization of this identity is as follows:
We may define the falling factorial as
and the corresponding rising factorial as
so, for example,
Then the binomial coefficients may be written as
while the corresponding multiset coefficient is defined by replacing the falling with the rising factorial:
Generalization to negative integers n[edit]

For any n,
In particular, binomial coefficients evaluated at negative integers n are given by signed multiset coefficients. In the special case 

For example, if n = −4 and k = 7, then r = 4 and f = 10:
Two real or complex valued arguments[edit]
The binomial coefficient is generalized to two real or complex valued arguments using the gamma function or beta function via
This definition inherits these following additional properties from 
moreover,
The resulting function has been little-studied, apparently first being graphed in (Fowler 1996). Notably, many binomial identities fail: 



Generalization to q-series[edit]
The binomial coefficient has a q-analog generalization known as the Gaussian binomial coefficient.
Generalization to infinite cardinals[edit]
The definition of the binomial coefficient can be generalized to infinite cardinals by defining:
where A is some set with cardinality 


Assuming the Axiom of Choice, one can show that 

In programming languages[edit]
The notation 
k ! n. The binomial coefficient is implemented in SciPy as scipy.special.comb.[18]
Naive implementations of the factorial formula, such as the following snippet in Python:
from math import factorial def binomial_coefficient(n: int, k: int) -> int: return factorial(n) // (factorial(k) * factorial(n - k))
are very slow and are useless for calculating factorials of very high numbers (in languages such as C or Java they suffer from overflow errors because of this reason). A direct implementation of the multiplicative formula works well:
def binomial_coefficient(n: int, k: int) -> int: if k < 0 or k > n: return 0 if k == 0 or k == n: return 1 k = min(k, n - k) # Take advantage of symmetry c = 1 for i in range(k): c = c * (n - i) // (i + 1) return c
(In Python, range(k) produces a list from 0 to k−1.)
Pascal’s rule provides a recursive definition which can also be implemented in Python, although it is less efficient:
def binomial_coefficient(n: int, k: int) -> int: if k < 0 or k > n: return 0 if k > n - k: # Take advantage of symmetry k = n - k if k == 0 or n <= 1: return 1 return binomial_coefficient(n - 1, k) + binomial_coefficient(n - 1, k - 1)
The example mentioned above can be also written in functional style. The following Scheme example uses the recursive definition
Rational arithmetic can be easily avoided using integer division
The following implementation uses all these ideas
(define (binomial n k) ;; Helper function to compute C(n,k) via forward recursion (define (binomial-iter n k i prev) (if (>= i k) prev (binomial-iter n k (+ i 1) (/ (* (- n i) prev) (+ i 1))))) ;; Use symmetry property C(n,k)=C(n, n-k) (if (< k (- n k)) (binomial-iter n k 0 1) (binomial-iter n (- n k) 0 1)))
When computing ![{textstyle {n choose k+1}=left[(n-k){n choose k}right]div (k+1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd616044be3a74725756d1abb6620ba141d9fd01)

Implementation in the C language:
#include <limits.h> unsigned long binomial(unsigned long n, unsigned long k) { unsigned long c = 1, i; if (k > n-k) // take advantage of symmetry k = n-k; for (i = 1; i <= k; i++, n--) { if (c/i > ULONG_MAX/n) // return 0 on potential overflow return 0; c = c / i * n + c % i * n / i; // split c * n / i into (c / i * i + c % i) * n / i } return c; }
Another way to compute the binomial coefficient when using large numbers is to recognize that
where 

See also[edit]
- Binomial transform
- Delannoy number
- Eulerian number
- Hypergeometric function
- List of factorial and binomial topics
- Macaulay representation of an integer
- Motzkin number
- Multiplicities of entries in Pascal’s triangle
- Narayana number
- Star of David theorem
- Sun’s curious identity
- Table of Newtonian series
- Trinomial expansion
Notes[edit]
- ^ Higham (1998)
- ^ Lilavati Section 6, Chapter 4 (see Knuth (1997)).
- ^ See (Graham, Knuth & Patashnik 1994), which also defines
for
. Alternative generalizations, such as to two real or complex valued arguments using the Gamma function assign nonzero values to
for
, but this causes most binomial coefficient identities to fail, and thus is not widely used by the majority of definitions. One such choice of nonzero values leads to the aesthetically pleasing “Pascal windmill” in Hilton, Holton and Pedersen, Mathematical reflections: in a room with many mirrors, Springer, 1997, but causes even Pascal’s identity to fail (at the origin).
- ^ Muir, Thomas (1902). “Note on Selected Combinations”. Proceedings of the Royal Society of Edinburgh.
- ^ This can be seen as a discrete analog of Taylor’s theorem. It is closely related to Newton’s polynomial. Alternating sums of this form may be expressed as the Nörlund–Rice integral.
- ^ Gradshteyn & Ryzhik (2014, pp. 3–4).
- ^ Boardman, Michael (2004), “The Egg-Drop Numbers”, Mathematics Magazine, 77 (5): 368–372, doi:10.2307/3219201, JSTOR 3219201, MR 1573776,
it is well known that there is no closed form (that is, direct formula) for the partial sum of binomial coefficients
. - ^ see induction developed in eq (7) p. 1389 in Aupetit, Michael (2009), “Nearly homogeneous multi-partitioning with a deterministic generator”, Neurocomputing, 72 (7–9): 1379–1389, doi:10.1016/j.neucom.2008.12.024, ISSN 0925-2312.
- ^ Ruiz, Sebastian (1996). “An Algebraic Identity Leading to Wilson’s Theorem”. The Mathematical Gazette. 80 (489): 579–582. arXiv:math/0406086. doi:10.2307/3618534. JSTOR 3618534. S2CID 125556648.
- ^ Benjamin & Quinn 2003, pp. 4−5
- ^ a b Farhi, Bakir (2007). “Nontrivial lower bounds for the least common multiple of some finite sequence of integers”. Journal of Number Theory. 125 (2): 393–411. arXiv:0803.0290. doi:10.1016/j.jnt.2006.10.017. S2CID 115167580.
- ^ Thomas M. Cover; Joy A. Thomas (18 July 2006). Elements of Information Theory. Hoboken, New Jersey: Wiley. ISBN 0-471-24195-4.
- ^ F. J. MacWilliams; N. J. A. Sloane (1981). The Theory of Error-Correcting Codes. Vol. 16 (3rd ed.). North-Holland. ISBN 0-444-85009-0.
- ^ Spencer, Joel; Florescu, Laura (2014). Asymptopia. Student mathematical library. Vol. 71. AMS. p. 66. ISBN 978-1-4704-0904-3. OCLC 865574788.
- ^ Spencer, Joel; Florescu, Laura (2014). Asymptopia. Student mathematical library. Vol. 71. AMS. p. 59. ISBN 978-1-4704-0904-3. OCLC 865574788.
- ^ see e.g. Ash (1990, p. 121) or Flum & Grohe (2006, p. 427).
- ^ Munarini, Emanuele (2011), “Riordan matrices and sums of harmonic numbers” (PDF), Applicable Analysis and Discrete Mathematics, 5 (2): 176–200, doi:10.2298/AADM110609014M, MR 2867317.
- ^ “scipy.special.comb”. SciPy Reference Guide. 2021-02-18. Retrieved 2021-03-02.
- ^ Bloomfield, Victor A. (2016). Using R for Numerical Analysis in Science and Engineering. CRC Press. p. 74. ISBN 978-1-4987-8662-1.
References[edit]
- Ash, Robert B. (1990) [1965]. Information Theory. Dover Publications, Inc. ISBN 0-486-66521-6.
- Benjamin, Arthur T.; Quinn, Jennifer J. (2003). Proofs that Really Count: The Art of Combinatorial Proof. Dolciani Mathematical Expositions. Vol. 27. Mathematical Association of America. ISBN 978-0-88385-333-7.
- Bryant, Victor (1993). Aspects of combinatorics. Cambridge University Press. ISBN 0-521-41974-3.
- Flum, Jörg; Grohe, Martin (2006). Parameterized Complexity Theory. Springer. ISBN 978-3-540-29952-3. Archived from the original on 2007-11-18. Retrieved 2017-08-28.
- Fowler, David (January 1996). “The Binomial Coefficient Function”. The American Mathematical Monthly. Mathematical Association of America. 103 (1): 1–17. doi:10.2307/2975209. JSTOR 2975209.
- Goetgheluck, P. (1987). “Computing Binomial Coefficients”. American Mathematical Monthly. 94 (4): 360–365. doi:10.2307/2323099. JSTOR 2323099.
- Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). Concrete Mathematics (Second ed.). Addison-Wesley. pp. 153–256. ISBN 0-201-55802-5.
- Gradshteyn, I. S.; Ryzhik, I. M. (2014). Table of Integrals, Series, and Products (8th ed.). Academic Press. ISBN 978-0-12-384933-5.
- Grinshpan, A. Z. (2010), “Weighted inequalities and negative binomials”, Advances in Applied Mathematics, 45 (4): 564–606, doi:10.1016/j.aam.2010.04.004
- Higham, Nicholas J. (1998). Handbook of writing for the mathematical sciences. SIAM. p. 25. ISBN 0-89871-420-6.
- Knuth, Donald E. (1997). The Art of Computer Programming, Volume 1: Fundamental Algorithms (Third ed.). Addison-Wesley. pp. 52–74. ISBN 0-201-89683-4.
- Singmaster, David (1974). “Notes on binomial coefficients. III. Any integer divides almost all binomial coefficients”. Journal of the London Mathematical Society. 8 (3): 555–560. doi:10.1112/jlms/s2-8.3.555.
- Shilov, G. E. (1977). Linear algebra. Dover Publications. ISBN 978-0-486-63518-7.
External links[edit]
- “Binomial coefficients”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Andrew Granville (1997). “Arithmetic Properties of Binomial Coefficients I. Binomial coefficients modulo prime powers”. CMS Conf. Proc. 20: 151–162. Archived from the original on 2015-09-23. Retrieved 2013-09-03.
This article incorporates material from the following PlanetMath articles, which are licensed under the Creative Commons Attribution/Share-Alike License: Binomial Coefficient, Upper and lower bounds to binomial coefficient, Binomial coefficient is an integer, Generalized binomial coefficients.








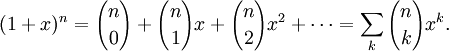
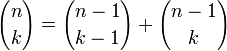
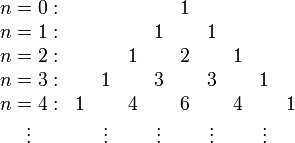
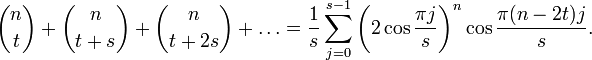

























































































































![{n choose k+1}=left[(n-k){n choose k}right]div (k+1)](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a767f5e82fcca7639c4ccc79decc17b539f1dff)
+{left[{n choose k} mathrm {mod} (k+1)right](n-k) over (k+1)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62dfa403a904aa342ee4d2a9e7d0783330b4bc61)

