Что такое истинное напряжение как его найти

Большая Энциклопедия Нефти и Газа

Истинное напряжение

Различают условное и истинное напряжение . Под условным напряжением понимается отношение силы, действующей на тело, к первоначальной площади его поперечного сечения. Истинное напряжение соответствует отношению действующей силы к площади поперечного сечения тела в каждый данный момент деформации. [16]

Изменение истинных напряжений и деформаций в интервале квазистатического разрушения зависит, помимо указанных свойств самого материала, также от величины действующей нагрузки. Последняя определяет остаточную накопленную деформацию ( остаточное сужение) при мягком нагружении. С уменьшением величины нагрузки остаточное сужение при разрушении снижается и истинные напряжения и деформации до момента образования трещины приближаются к условным. [17]

Кривая истинных напряжений у сталей аустенитного типа лежит значительно выше, чем у других сталей. [18]

Диаграмма истинных напряжений в координатах s — q, типичная для большинства пластичных металлов, представлена на фиг. [19]

Определение истинных напряжений является одним из важных условий для оценки эксплуатационных возможностей деталей и конструкций. [20]

Эпюры истинных напряжений получены сложением номинальных и остаточных напряжений. [21]

Диаграмма истинных напряжений , полученных делением нагрузок на истинную площадь поперечного сечения, показана на рис. 23 штрих-пунктирной линией. [23]

Зависимость истинных напряжений от деформаций s показана в виде кривой ОВ С диаграммы растяжения на фиг. Продолжить кривую a F ( e), представляющую истинные напряжения, за точку С, соответствующую максимуму нагрузки Р или напряжения о0, допустимо лишь при условии, если мы измерим площади минимальных поперечных сечений в шейке образца. [24]

Расчет истинного напряжения в точках произведен с по-мощью метода фотоупругости. [26]

Кривая истинных напряжений в начале мало отличается от кривой напряжений условной диаграммы растяжений, так как до предела текучести изменения площади поперечного сечения очень малы. За пределом текучести, особенно после достижения предела прочности и образования HI образно шейки кривая ипинных напряжении резко направляется вверх. [27]

Диаграмма истинных напряжений для стали 10 представлена на фиг. [28]

Величина истинного напряжения стра3р, при котором наступает разрушение металла при осевом растяжении, также может быть принята за характеристику прочности металла в данном состоянии вне зависимости от схемы напряженного состояния. Поэтому при анализе поведения металла при различных схемах напряженного состояния будем считать, что разрушение должно наступать тогда, когда наибольшее главное напряжение а достигнет величины огразр, вызывающей разрушение при осевом растяжении. [29]

Величины истинных напряжений внесены в последний столбец таблицы. [30]

Источник

iSopromat.ru

Диаграмма напряжений показывает основные механические характеристики материалов (в основном металлов), такие как: предел пропорциональности, текучести, прочности и т.д.

Для построения диаграммы используют диаграмму растяжения испытуемого образца, изготовленного из материала, характеристики которого требуется изучить.

После эксперимента по испытанию на растяжение, на полученной диаграмме F-Δl отмечаются несколько характерных точек, в которых определяются значения растягивающих усилий F и соответствующие им абсолютные деформации Δl .

Далее для полученных значений точек диаграммы определяются соответствующие им нормальные напряжения σ , по формуле:

где:
F_i — значение растягивающей силы в характерной точке диаграммы;
A₀ — площадь поперечного сечения рабочей части образца,

где l₀ — начальная длина рабочей части испытуемого образца.

Затем по полученным данным в системе координат σ-ε строится диаграмма напряжений (рис. 1)

Рис. 1 Условная и истинная диаграмма напряжений для малоуглеродистой стали

По этой диаграмме определяются следующие механические характеристики материала:

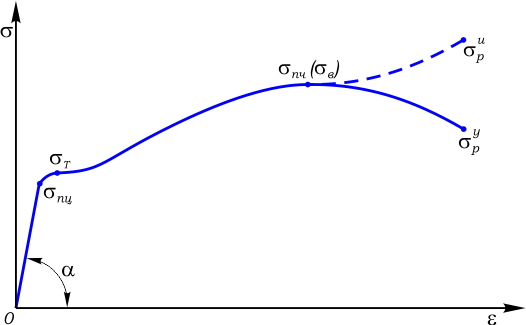
σ _пц — предел пропорциональности
Определяется как крайняя верхняя точка начального прямолинейного участка диаграммы.

σ_т — предел текучести
Точка после которой линия диаграммы некоторое время движется параллельно оси деформаций ε .

Практически горизонтальный участок диаграммы, следующий за пределом текучести называется площадкой текучести.

σ _пч — предел прочности ( σ _в — временное сопротивление)
Высшая точка условной диаграммы;

σ _р — напряжение в момент разрыва образца ( σ _р у — условное и σ _р и — истинное).

Конечная точка диаграммы, при которой происходит разрыв образца.

здесь A_ш — площадь поперечного сечения в области «шейки» образца.

При более тонких испытаниях по данной диаграмме можно определить предел упругости стали.

На рисунке 1 штриховой линией показан фрагмент истинной диаграммы напряжений. Возрастание напряжений после прохождения предела прочности объясняется тем, что в этот момент в рабочей части образца образуется локальное утоньшение («шейка») уменьшающая его площадь поперечного сечения A , что в свою очередь приводит к увеличению напряжений при уменьшающейся величине растягивающей силы.

Кроме того, по диаграмме напряжений можно приближенно определить величину модуля упругости I рода материала образца:

он определяется как отношение напряжений и относительных деформаций, для любой точки диаграммы расположенной от ее начала до предела пропорциональности, либо как тангенс угла наклона начального участка диаграммы к оси ε .

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Истинное напряжение

Смотреть что такое «Истинное напряжение» в других словарях:

истинное напряжение — Значение, полученное отношением прикладываемой к телу нагрузки к площади поперечного сечения, на которую эта нагрузка действует. [http://www.manual steel.ru/eng a.html] Тематики металлургия в целом EN true stress … Справочник технического переводчика

истинное напряжение — [effective stress] нормальное напряжение, отнесенное к действительной площади поперечного сечения образца в каждый момент нагружения; Смотри также: Напряжение электрическое напряжение условное напряжение … Энциклопедический словарь по металлургии

истинное напряжение при разрушении — истинный предел прочности — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы истинный предел прочности EN true fracture stress … Справочник технического переводчика

истинное напряжение разрушения — [effective rupture stress] отношение нагрузки, приложенной к образцу (изделию) в момент разрушения, к его конечному сечению; Смотри также: Напряжение электрическое напряжение условное напряжение напряжение течения … Энциклопедический словарь по металлургии

напряжение течения — [flow stress] истинное напряжение, вызывающее стабильное пластическое течение металла при заданных условиях деформирования; Смотри также: Напряжение электрическое напряжение … Энциклопедический словарь по металлургии

напряжение волочения — [drawing stress] основная энергосиловая характеристика волочения отношение продольной силы волочения Р к площади поперечного сечения изделия на выходе из волоки Fк, называемая напряжение волочения σ. Должно быть: σвол Энциклопедический словарь по металлургии

Напряжение — [stress] 1. Мера внутренних сил, возникающих в образце (изделии) под влиянием внешних воздействий, равная отношению величины равнодействвующей силы к площади ее приложения (механическое напряжение); размерность МПа: Смотри также: электрическое… … Энциклопедический словарь по металлургии

электрическое напряжение — [voltage] разность потенциалов между двумя точками электрической цепи; единица измерения 1В. Смотри также: Напряжение условное напряжение напряжение течения среднее напряжение цикла … Энциклопедический словарь по металлургии

условное напряжение — [unit stress] напряжение, рассчитанное для исходной геометрии образца (изделия) без учета ее изменения под действием приложенного напряжения (1.); Смотри также: Напряжение электрическое напряжение … Энциклопедический словарь по металлургии

среднее напряжение цикла — [mean cyclic stress] алгебраическая полусумма максимальных и минимальных напряжений цикла; Смотри также: Напряжение электрическое напряжение условное напряжение напряжение течения … Энциклопедический словарь по металлургии

Источник

Напряжения и деформации в стали

Когда усилие или комбинация усилий прилагается к материалу, в том числе, к стали, то этот материал – сталь – реагирует на это проявлением деформации, то есть изменением своих размеров, часто очень сложным образом.

Что такое деформация

Каждый из нас видел по телевизору, как прыгают с высоты метров этак двухсот – с моста или специальной платформы – экстремалы-прыгуны, которые привязаны за ноги к резиновому канату. Этот резиновый канат растягивается прямо у нас на глазах и хорошо видно как его сечение значительно уменьшается. Этот канат растягивается так, чтобы не ударить прыгуна об землю, а потом обратно сжимается. В этом примере деформация резинового каната – изменение его длины и толщины – хорошо видна.

Но так бывает не всегда. Например, если какой-то достаточно тяжелый груз подвесить на вертикальной стальной проволоке, то длина этой проволоки, конечно же, увеличиться, а ее поперечное сечение – уменьшится. Однако эту деформацию – изменение размеров проволоки — не так просто заметить. Для этого нужны специальные тщательные измерения длины и диаметра этой проволоки, как до подвешивания груза, так и тогда, когда он на ней уже висит.

Механические свойства материала, в том числе, стали, описывают взаимоотношение между напряжениями, которые действуют на материал из-за приложенных нагрузок и деформациями, которые этот материал испытывает в результате этих напряжений.

Что такое напряжение

Понятие напряжения в самой общей форме – это усилие или нагрузка, поделенная на площадь, на которую она действует. Здесь лучше выразиться математически, что дает следующее выражение:

где F – усилие (сила), которая воздействует на площадь А,
А – площадь, на которую воздействует усилие F,
σ – напряжение на площадке площадью А.

Напряжения в наше время выражают в единицах МПа, что означает миллион (10 6 ) единиц Н/м 2 (ньютон на метр квадратный).

Существует два различных способа описания этих самых напряжений: инженерные и истинные.

Инженерные напряжения

Инженерные напряжения обычно применяют в инженерных расчетах. Они основаны на исходной площади поперечного сечения детали или изделия, которое рассматривается. Поскольку инженерные напряжения рассчитываются для исходной – не нагруженной – площади, то они не учитывают, что эта площадь поперечного сечения изменилась после того как к детали было приложена нагрузка. Когда материал находится под нагрузкой, то результирующее изменение площади поперечного сечения зависит от механических свойств материала и величины прилагаемой нагрузки.

Истинные напряжения

Истинные напряжения основаны на фактической в каждый момент – мгновенной – площади поперечного сечения. Поэтому это, в принципе, более точный метод описания напряжений. Однако поскольку величину истинных напряжений определить намного труднее, чем инженерных напряжений, то на практике их редко применяют.

Деформация – безразмерное число

Применение понятия «деформация» позволяет количественно описывать изменения размеров и формы тела, которые возникают при приложении напряжений, которые, в свою очередь, возникают при приложении некоторой нагрузки. Важно отметить, что деформация – это «чистое», безразмерное число. У деформации нет каких-либо единиц измерения. Чтобы вычислить деформацию нужно сравнить начальные, исходные размеры или форму тела до приложения нагрузки с теми же размерами или формой того же тела под нагрузкой.

Формула, по которой вычисляют деформацию, имеет величины одной и той же размерности (метры, сантиметры, миллиметры) как в знаменателе, так и в числителе. Поэтому, понятно еще из школьной физики, что эти размерные единицы взаимно сокращаются, и в результате мы получаем безразмерное число. Эта процедура хорошо видна при вычислении напряжений и деформаций для простого испытания на растяжение.

Испытание металлов на растяжение

При обычном инженерном испытании металлических материалов при растяжении, в том числе, стали, получают инженерную же диаграмму напряжение-деформация. Эта диаграмма строится по результатам измерений нагрузка-удлинение, которые выполняют на образце, который постепенно подвергается растяжению (рисунок 1)

Рисунок 1 – Стандартный образец для испытания на растяжение, который применяют для определения механических свойств металлических материалов, в том числе, сталей.

Диаграмма растяжения

Инженерное напряжение σ, которое применяют на диаграмме напряжение-деформация на рисунке 2, является средним или номинальным напряжением в разрывном образце. Его получают путем деления величины нагрузки F на исходную – не нагруженную – площадь А₀ поперечного сечения этого образца.

Рисунок 2 – Инженерная диаграмма напряжение-деформация. Чаще ее называют диаграммой растяжения. Пересечение пунктирной линии с диаграммой напряжение-деформация дает величину предела текучести при остаточной деформации, обычно, 0,2 %.

По мере увеличения напряжения в разрывном образце расстояние между метками базовой длины изменяется под воздействием приложенных напряжений. Результирующая деформация ɛ, которая указана на инженерной диаграмме напряжение-деформация, является средней или номинальной линейной – одноосной – деформацией. Величину этой деформации получают путем деления изменения базовой длины образца δ на исходную базовую длину образца L₀:

Поскольку и инженерное напряжение (σ) и деформация (ɛ) получены путем деления нагрузки на образец и удлинения образца на одну и ту же постоянную величину L₀, то форма диаграммы нагрузка-удлинение и напряжение-деформация имеют одинаковую форму.

Форма и размеры диаграммы растяжения стали зависит от:

• химического состава стали,
• виде термической обработки,
• режимов пластического деформирования,
• скорости нагружения,
• температуры и
• напряженного состояния в ходе испытания на растяжение.

Механические свойства стали чаще всего определяют именно путем испытания растяжение, которое описано выше. Характеристики стали, которые обычно применяют для описания диаграммы растяжения конкретной стали включают:

• предел прочности (временное сопротивление разрыву),
• предел текучести,
• удлинение базовой длины образца (в процентах),
• сужение площади поперечного сечения образца (в процентах).

Различные типы испытаний, которые включают применение различных нагрузок на стальной образец, применяют также для определения других механических свойств стали. Примерами таких механических свойств стали являются модуль упругости, твердость, сопротивление усталости и ударная вязкость.

Все механические свойства стали

Почти полный список механических свойств для стали включает:

• Твердость. Мера сопротивления вдавливанию
• Линейные коэффициенты упругости для растягивающих, сжимающих и сдвиговых нагрузок
• Предел текучести (при растягивающих, сжимающих и сдвиговых нагрузках). Показывает уровень напряжения, при котором возникают необратимые пластические деформации
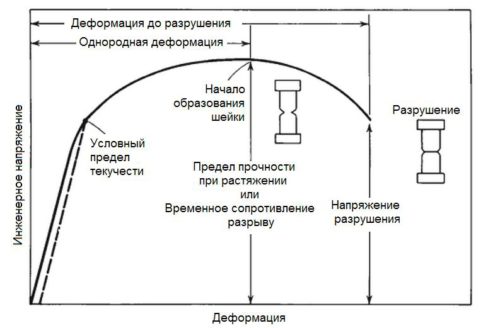
• Предел прочности (при растягивающих, сжимающих и сдвиговых нагрузках). Показывает максимальные инженерные напряжения, которые материал может выдержать без разрушения. Предел прочности при растяжении – временное сопротивление разрыву – обычно связывают с началом образования шейки на разрывном образце (см. рисунок 2)
• Усталостная прочность. Показывает уровень циклических напряжений, которые вызывают разрушение из-за усталости металла после определенного количества циклов нагружения, например, 1 миллион
• Ударная вязкость. Показывает уровень поглощения ударной энергии от нагрузок, которые способен поглотить металл до разрушения
• Вязкость разрушения. Показывает уровень сопротивления разрушению, когда в изделии присутствуют дефекты и концентраторы напряжений
• Сопротивление высокотемпературной ползучести и разрушению.
• Износостойкость.

Источник

Истинное напряжение

Cтраница 2

Различают условное и истинное напряжение. Под условным напряжением понимается отношение силы, действующей на тело, к первоначальной площади его поперечного сечения. Истинное напряжение соответствует отношению действующей силы к площади поперечного сечения тела в каждый данный момент деформации.
 [16]

Изменение истинных напряжений и деформаций в интервале квазистатического разрушения зависит, помимо указанных свойств самого материала, также от величины действующей нагрузки. Последняя определяет остаточную накопленную деформацию ( остаточное сужение) при мягком нагружении. С уменьшением величины нагрузки остаточное сужение при разрушении снижается и истинные напряжения и деформации до момента образования трещины приближаются к условным.
 [17]

Кривая истинных напряжений у сталей аустенитного типа лежит значительно выше, чем у других сталей.
 [18]

Диаграмма истинных напряжений в координатах s – q, типичная для большинства пластичных металлов, представлена на фиг.
 [19]

Определение истинных напряжений является одним из важных условий для оценки эксплуатационных возможностей деталей и конструкций.
 [20]

Эпюры истинных напряжений получены сложением номинальных и остаточных напряжений.
 [21]

Диаграмма истинных напряжений, полученных делением нагрузок на истинную площадь поперечного сечения, показана на рис. 23 штрих-пунктирной линией.
 [23]

Зависимость истинных напряжений от деформаций s показана в виде кривой ОВ С диаграммы растяжения на фиг. Продолжить кривую a F ( e), представляющую истинные напряжения, за точку С, соответствующую максимуму нагрузки Р или напряжения о0, допустимо лишь при условии, если мы измерим площади минимальных поперечных сечений в шейке образца.
 [24]

Расчет истинного напряжения в точках произведен с по-мощью метода фотоупругости.
 [26]

Кривая истинных напряжений в начале мало отличается от кривой напряжений условной диаграммы растяжений, так как до предела текучести изменения площади поперечного сечения очень малы. За пределом текучести, особенно после достижения предела прочности и образования HI образно шейки кривая ипинных напряжении резко направляется вверх.
 [27]

Диаграмма истинных напряжений для стали 10 представлена на фиг.
 [28]

Величина истинного напряжения стра3р, при котором наступает разрушение металла при осевом растяжении, также может быть принята за характеристику прочности металла в данном состоянии вне зависимости от схемы напряженного состояния. Поэтому при анализе поведения металла при различных схемах напряженного состояния будем считать, что разрушение должно наступать тогда, когда наибольшее главное напряжение а достигнет величины огразр, вызывающей разрушение при осевом растяжении.
 [29]

Величины истинных напряжений внесены в последний столбец таблицы.
 [30]

Страницы:  

   1

   2

   3

   4

Диаграммы условных и истинных напряжений

Диаграмма растяжения в осях Δl и P
является по существу характеристикой
образца из данного материала, так как
при одном и том же значении силы P
величина удлинения зависит от поперечных
и продольных размеров образца. Чтобы
исключить влияние размеров образца и
получить характеристику материала,
диаграмму растяжения строят в координатах
σ – ε.

При переходе от нагрузок P к напряжениям
σ и от абсолютных удлинений Δl
к относительным ε обычно пренебрегают
изменением площади сечения образца в
процессе растяжения, а также неравномерностью
распределения деформаций по длине его
рабочей части после образования шейки.
Подсчитывают σ делением нагрузки
P на первоначальную площадь F_o
сечения образца, а ε – делением
удлинения всей его рабочей части на ее
первоначальную длину l_o.
Полученная таким путем диаграмма
называется диаграммой условных
напряжений, по характеру она не отличается
от диаграммы в осях P – Δl.

Диаграмма условных напряжений для
малоуглеродистой стали показана на
Рисунок 4.6. Уравнение линейного участка
этой диаграммы на начальной стадии
нагружения σ = Eε представляет собой
уже известную математическую запись
закона Гука при одноосном растяжении.
Следовательно, численно модуль упругости
равен тангенсу угла α наклона к оси
абсцисс прямолинейного участка диаграммы
растяжения.

Диаграмма растяжения, по оси ординат
которой откладывается напряжение,
полученное делением силы на наименьшую
площадь сечения образца, а по оси абсцисс
– наибольшее удлинение в данный момент
нагружения, называется диаграммой
истинных напряжений. Эта диаграмма
показана на Рисунок4.6 пунктиром. Здесь
падения напряжений за точкой C не
наблюдается, так как площадь сечения в
шейке уменьшается быстрее, чем падает
нагрузка, поэтому средние напряжения
в этом месте возрастают. Вследствие
образования шейки распределение
напряжений по сечению становится
неравномерным, а частицы материала в
этом месте испытывают растяжение не
только в продольном, но также в радиальном
и окружном направлениях. Это приводит
к образованию внутри шейки поперечной
трещины. Различие диаграмм условных и
истинных напряжений становится
значительным только после образования
шейки.

Рисунок 4.6 Диаграмма условных напряжений

Механические характеристики материалов

Под механическими характеристиками
подразумеваются значения напряжений
и деформаций, соответствующие определенным
точкам на диаграмме условных напряжений.

Пределом пропорциональности σ_пц
называется наибольшее напряжение, до
которого деформации прямо пропорциональны
напряжениям.

Пределом упругости σ_у
называется напряжение, до которого
материал не получает остаточных
деформаций.

Пределом текучести σ_т называется
напряжение, при котором деформации
растут без заметного увеличения нагрузки.

Пределом прочности, или временным
сопротивлением σ_в называется
максимальное напряжение (подсчитанное
по первоначальной площади сечения
образца), выдерживаемое материалом при
растяжении. Его величина определяется
ординатой точки C условной диаграммы
(см. Рисунок 4.6).

При экспериментальном определении
величин пределов пропорциональности
и упругости вносится определенный
элемент условности. Объясняется это
тем, что начало отклонения от линейной
зависимости, как и начало образования
остаточных деформаций, будет отмечено
тем раньше, чем выше точность измерения
деформаций.

Поэтому под пределом пропорциональности
σ_пц понимается напряжение,
при котором отступление от линейной
зависимости достигает определенной
величины, устанавливаемой техническими
условиями.

Пределом упругости считается напряжение,
при котором остаточные деформации
достигают заранее установленной величины
в пределах 0.001-0.005%. Условный предел
упругости при остаточной деформации
0.005% обозначается σ_0,005.

Для материалов, не имеющих площадки
текучести, в качестве предела текучести
условно принимается напряжение, при
котором остаточные деформации составляют
0.2 или 0.3% от первоначальной длины образца.
Условный или, иначе, технический предел
текучести в соответствии с допуском на
остаточную деформацию обозначается
σ_0,2 или σ_0,3.

В теоретических исследованиях индексы
0.2 и 0.3 обычно опускаются и условный
предел текучести обозначается символом
σ_т. Предел текучести является
одной из основных характеристик
материала. Пластические свойства
материала, то есть способность к
образованию остаточных деформаций,
характеризуются величиной остаточного
удлинения образца при разрыве

,

(4.7)

а также относительным уменьшением
площади сечения образца в шейке

,

(4.8)

где l₁, F₁ –
длина рабочей части образца и площадь
наименьшего сечения шейки разорванного
образца, соответственно; l_o,
F_o – их величины до нагружения.

Основные механические характеристики
применяемых в технике материалов
приводятся в справочной литературе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Когда усилие или комбинация усилий прилагается к материалу, в том числе, к стали, то этот материал – сталь – реагирует на это проявлением деформации, то есть изменением своих размеров, часто очень сложным образом.

Что такое деформация

Каждый из нас видел по телевизору, как прыгают с высоты метров этак двухсот – с моста или специальной платформы – экстремалы-прыгуны, которые привязаны за ноги к резиновому канату. Этот резиновый канат растягивается прямо у нас на глазах и хорошо видно как его сечение значительно уменьшается. Этот канат растягивается так, чтобы не ударить прыгуна об землю, а потом обратно сжимается. В этом примере деформация резинового каната – изменение его длины и толщины – хорошо видна.

Но так бывает не всегда. Например, если какой-то достаточно тяжелый груз подвесить на вертикальной стальной проволоке, то длина этой проволоки, конечно же, увеличиться, а ее поперечное сечение – уменьшится. Однако эту деформацию – изменение размеров проволоки — не так просто заметить. Для этого нужны специальные тщательные измерения длины и диаметра этой проволоки, как до подвешивания груза, так и тогда, когда он на ней уже висит.

Механические свойства материала, в том числе, стали, описывают взаимоотношение между напряжениями, которые действуют на материал из-за приложенных нагрузок и деформациями, которые этот материал испытывает в результате этих напряжений.

Что такое напряжение

Понятие напряжения в самой общей форме – это усилие или нагрузка, поделенная на площадь, на которую она действует. Здесь лучше выразиться математически, что дает следующее выражение:

σ = F/A,

где F – усилие (сила), которая воздействует на площадь А,
А – площадь, на которую воздействует усилие F,
σ – напряжение на площадке площадью А.

Напряжения в наше время выражают в единицах МПа, что означает миллион (10⁶) единиц Н/м² (ньютон на метр квадратный).

Существует два различных способа описания этих самых напряжений: инженерные и истинные.

Инженерные напряжения

Инженерные напряжения обычно применяют в инженерных расчетах. Они основаны на исходной площади поперечного сечения детали или изделия, которое рассматривается. Поскольку инженерные напряжения рассчитываются для исходной – не нагруженной – площади, то они не учитывают, что эта площадь поперечного сечения изменилась после того как к детали было приложена нагрузка. Когда материал находится под нагрузкой, то результирующее изменение площади поперечного сечения зависит от механических свойств материала и величины прилагаемой нагрузки.

Истинные напряжения

Истинные напряжения основаны на фактической в каждый момент – мгновенной – площади поперечного сечения. Поэтому это, в принципе, более точный метод описания напряжений. Однако поскольку величину истинных напряжений определить намного труднее, чем инженерных напряжений, то на практике их редко применяют.

Деформация – безразмерное число

Применение понятия «деформация» позволяет количественно описывать изменения размеров и формы тела, которые возникают при приложении напряжений, которые, в свою очередь, возникают при приложении некоторой нагрузки. Важно отметить, что деформация – это «чистое», безразмерное число. У деформации нет каких-либо единиц измерения. Чтобы вычислить деформацию нужно сравнить начальные, исходные размеры или форму тела до приложения нагрузки с теми же размерами или формой того же тела под нагрузкой.

Формула, по которой вычисляют деформацию, имеет величины одной и той же размерности (метры, сантиметры, миллиметры) как в знаменателе, так и в числителе. Поэтому, понятно еще из школьной физики, что эти размерные единицы взаимно сокращаются, и в результате мы получаем безразмерное число. Эта процедура хорошо видна при вычислении напряжений и деформаций для простого испытания на растяжение.

Испытание металлов на растяжение

При обычном инженерном испытании металлических материалов при растяжении, в том числе, стали, получают инженерную же диаграмму напряжение-деформация. Эта диаграмма строится по результатам измерений нагрузка-удлинение, которые выполняют на образце, который постепенно подвергается растяжению (рисунок 1)

Рисунок 1 – Стандартный образец для испытания на растяжение, который применяют для определения механических свойств металлических материалов, в том числе, сталей.

Диаграмма растяжения

Инженерное напряжение σ, которое применяют на диаграмме напряжение-деформация на рисунке 2, является средним или номинальным напряжением в разрывном образце. Его получают путем деления величины нагрузки F на исходную – не нагруженную – площадь А₀ поперечного сечения этого образца.

σ = F/A₀.

Рисунок 2 – Инженерная диаграмма напряжение-деформация. Чаще ее называют диаграммой растяжения. Пересечение пунктирной линии с диаграммой напряжение-деформация дает величину предела текучести при остаточной деформации, обычно, 0,2 %.

По мере увеличения напряжения в разрывном образце расстояние между метками базовой длины изменяется под воздействием приложенных напряжений. Результирующая деформация ɛ, которая указана на инженерной диаграмме напряжение-деформация, является средней или номинальной линейной – одноосной – деформацией. Величину этой деформации получают путем деления изменения базовой длины образца δ на исходную базовую длину образца L₀:

ɛ = δ/L₀ = ΔL/L₀ = (L — L₀)/L₀

Поскольку и инженерное напряжение (σ) и деформация (ɛ) получены путем деления нагрузки на образец и удлинения образца на одну и ту же постоянную величину L₀, то форма диаграммы нагрузка-удлинение и напряжение-деформация имеют одинаковую форму.

Форма и размеры диаграммы растяжения стали зависит от:

• химического состава стали,
• виде термической обработки,
• режимов пластического деформирования,
• скорости нагружения,
• температуры и
• напряженного состояния в ходе испытания на растяжение.

Механические свойства стали чаще всего определяют именно путем испытания растяжение, которое описано выше. Характеристики стали, которые обычно применяют для описания диаграммы растяжения конкретной стали включают:

• предел прочности (временное сопротивление разрыву),
• предел текучести,
• удлинение базовой длины образца (в процентах),
• сужение площади поперечного сечения образца (в процентах).

Различные типы испытаний, которые включают применение различных нагрузок на стальной образец, применяют также для определения других механических свойств стали. Примерами таких механических свойств стали являются модуль упругости, твердость, сопротивление усталости и ударная вязкость.

Все механические свойства стали

Почти полный список механических свойств для стали включает:

• Твердость. Мера сопротивления вдавливанию
• Линейные коэффициенты упругости для растягивающих, сжимающих и сдвиговых нагрузок
• Предел текучести (при растягивающих, сжимающих и сдвиговых нагрузках). Показывает уровень напряжения, при котором возникают необратимые пластические деформации
• Предел прочности (при растягивающих, сжимающих и сдвиговых нагрузках). Показывает максимальные инженерные напряжения, которые материал может выдержать без разрушения. Предел прочности при растяжении – временное сопротивление разрыву – обычно связывают с началом образования шейки на разрывном образце (см. рисунок 2)
• Усталостная прочность. Показывает уровень циклических напряжений, которые вызывают разрушение из-за усталости металла после определенного количества циклов нагружения, например, 1 миллион
• Ударная вязкость. Показывает уровень поглощения ударной энергии от нагрузок, которые способен поглотить металл до разрушения
• Вязкость разрушения. Показывает уровень сопротивления разрушению, когда в изделии присутствуют дефекты и концентраторы напряжений
• Сопротивление высокотемпературной ползучести и разрушению.
• Износостойкость.

Расчет по напряжениям смятия условный, так как не учитывает истинного характера распределения напряжений. В этом случае допускаемые напряжения [а]с = 2 Н/мм .  [c.271]

Следует отличать истинные напряжения от условных. Истинные напряжения определяют, относя силу, приложенную к образцу, к фактическому значению площади сечения, изменяющейся при напряжениях, способных вызвать достаточную деформацию. Например, при растяжении образца в результате больших деформаций постепенно образуется шейка , как это показано на рис. 4.2.  [c.116]

После достижения предела прочности в одном месте образца появляется еле заметное на глаз сужение (шейка), которое становится все более и более заметным. Площадь сечения шейки быстро уменьшается и вскоре на этом месте происходит разрушение (рис. 2.92). С появлением шейки нагрузка начинает падать, поэтому и условные напряжения на участке ВЕ падают, так как диаграмму строят без учета изменения площади сечения образца. Напряжение в точке Е диаграммы называют напряжением разрушения материала. Но это напряжение чисто условное. Истинное напряжение в момент разрушения значительно превосходит не только условное напряжение, но и предел прочности и равно отношению разрушающей нагрузки к площади сечения шейки.  [c.276]

При рассмотрении задач о растяжении упругих стержней предполагалось, что деформации малы. Однако пластические деформации металлов и упругие деформации таких материалов как резина могут быть значительны. Посмотрим, каким образом может повлиять учет значительной величины деформаций на приведенные выше рассуждения ). Прежде всего остановимся на понятии напряжения. При растяжении поперечные размеры стержня уменьшаются, следовательно, уменьшается площадь сечения. Истинное напряжение есть сила, поделенная на фактическую площадь поперечного сечения таким образом, оно зависит не только от величины силы, но и от величины вызванной этой силой деформации. Чтобы построить диаграмму с — е, нужно во время опыта непрерывно измерять поперечный размер стержня, что бывает затруднительно. Часто под напряжением понимают силу, поделенную на первоначальную площадь поперечного сечения, определенное таким образом напряжение называется условным, будем обозначать его Оо.  [c.62]

Напряжения, которыми оперируют в механических испытаниях, могут быть условными и истинными. Условные напряжения определяются как отношение действующей силы к начальной площади поперечного сечения (а = Р Р , а истинные — к текущей (5 = PIP) [1, 45, 46]. Физический смысл имеют истинные напряжения, они отражают состояние металла в каждый данный момент деформации, следовательно, являются характеристиками деформационного упрочнения.  [c.28]

Чем отличаются истинные напряжения от условных  [c.80]

Механическое напряжение называется условным, если при его вычислении сила относится к площади сечения в недеформированном состоянии, и истинным, если учтено изменение площади при деформировании.  [c.85]

Истинное напряжение тоже можно выразить через условное напряжение и условную деформацию. Чтобы сделать это, введем экспериментально подтвержденное предположение, что в процессе нагружения в пластической области объем материала не изменяется, т, е. что  [c.108]

Что такое условное напряжение, истинное напряжен 1е, сопротивление деформации  [c.161]

Временное сопротивление (а ) характеризует максимальное напряжение, предшествующее разрушению образца. Различают напряжения условные и истинные. Условным напряжением называют отношение величины нагрузки к исходному сечению образца истинным – к сечению, которое образец приобрел к моменту достижения данной нагрузки. Диаграммы растяжения пластичных металлов с условными напряжениями отличаются от диаграмм с истинными напряжениями.  [c.52]

При дальнейшем растяжении деформация по длине образца становится неравномерной, сосредоточиваясь в области шейки. Точке D на истинной диаграмме и точке D — на условной соответствует разрыв образца. Напряжение к называют истинным сопротивлением разрыву. Оно характеризует прочность материала при статических нагрузках. При разрушении образца с образованием выраженной шейки напряжение также условно в связи с неравномерностью его распределения по сечению шейки.  [c.10]

Автор всюду в упомянутых выше собственных исследованиях отдает предпочтение использованию тензоров условных напряжений и де( юрмаций, считая, что именно при этом условии отчетливо обнаруживаются установленные им закономерности. В тех местах, где автор книги использует для подтверждения своих выводов результаты экспериментов других исследователей, представленные через тензор напряжений Коши и логарифмические деформации, он производит переход к тензору условных напряжений и условным деформациям. Отмеченный факт вызывает некоторое удивление. Казалось бы, что в терминах истинных напряжений и дес юрмаций, лучше отражающих природу напряженно-деформированного сос-  [c.17]

Людвик и Шой сделали заключение, что использование зависимости между напряжением Коши ( истинным напряжением) и условной деформацией (отнесенной к первоначальной плош,ади) обеспечивало одинаковый отклик при растяжении и сжатии ).  [c.153]

Корреляция, которую установили Людвик и Шой, касалась истинного напряжения и условной деформации, а корреляция, установленная Тэйлором, была проведена для условного напряжения и логарифмической деформации. В подавляющей части литературы, посвященной экспериментам, с самого начала выполнения исследований в основном было принято описывать результаты в терминах редуцированного напряжения в зависимости от натуральной или логарифмической деформации, которые технологи называли истинным напряжением и истинной деформацией.  [c.154]

Почти все эксперименты моей лаборатории были выполнены на одной из различных специально сконструированных машин с нагружением мертвой нагрузкой и спроектированных для осуществления либо постоянства скорости нагружения, либо определенных историй возрастания нагрузки. Скорости деформации изменялись в пределах от 10 до 10 с . Результаты, взятые из других источников — 177 испытаний 19 металлических элементов и 5 двойных сплавов,— даны в терминах истинное напряжение и истинная деформация. Чтобы выполнить желаемое сравнение, я пересчитал все данные, полученные в опытах с отожженными поликристаллами, описание которых было найдено мною в литературе, представив их в условных напряжениях и условных деформациях при этом не было исключено ни одно из тех описаний, где были приведены детали первоначальных расчетов, позволявшие любые результаты вновь полностью находить при построении определяющих уравнений рациональной механики.  [c.161]

Сопротивление материала значительной пластической деформации характеризуется временным сопротивлением (пределом прочности). Временное сопротивление = PJF – условное напряжение, соответствующее максимальной нагрузке, выдерживаемой образцом в процессе испытания на растяжение. Образование и развитие шейки приводит к уменьшению условного и увеличению истинного напряжения. Истинное напряжение разрыву PJF , где F – поперечное сечение образца в момент разрыва, достигает максимального значения в момент разрушения. Ранее эта характеристика не использовалась в инженерной практике при аттестации качества стали.  [c.81]

Заметное отклонение величин истинных напряжений от условных наблюдается, начиная от площадки текучести, но отклонения становятся особенно большими после достижения нагрузкой разрушающего значения.  [c.28]

Как мы видели выше, диаграмма напряжений при растяжении хотя и характеризует свойства материалов, но получаемые по ней механические характеристики являются условными. Если в начале испытаний площадь поперечного сечения образца почти не изменяется, то, начиная с напряжений, равных пределу текучести, наступает заметное изменение площади. Поэтому все ординаты кривой выше предела текучести дают не истинные напряжения, а условные, отнесенные не к действительной площади поперечного сечения, а к первоначальной.  [c.30]

Диаграмма напряжений истинных 30 –условных 25  [c.521]

До точки, соответствующей пределу прочности при статической нагрузке, истинная диаграмма растяжения е ст = / (5) и обычная диаграмма растяжения 8 = / (сг) мало отличаются одна от другой, так как более значительная разница в величинах относительного удлинения наблюдается только после начала образования шейки на образце, соответствующего достижению состояния неустойчивости пластической деформации при напряжении, равном условному пределу прочности.  [c.189]

Следует отличать истинные напряжения от условных. Истинные напряжения (нормальные 5 и касательные I) определяют отнесением к фактическому значению площади сечения, а условные (а ИТ соответственно) – к начальному.  [c.141]

Различают условное и истинное напряжение. Под условным напряжением понимается отношение силы, действующей на тело, к первоначальной площади его поперечного сечения. Истинное напряжение соответствует отношению действующей силы к площади поперечного сечения тела в каждый данный момент деформации. Разница между условным и истинным напряжением тем значительнее, чем больше деформация тела (уменьшение сечения).  [c.13]

Какие диаграммы напряжений называются условными и какие — истинными  [c.105]

При коррозионной усталости наблюдается снижение предела усталости но сравнению с пределом усталости металла в отсутствие коррозионного воздействия агрессивной среды. Пределом коррозионной усталости или коррозионной выносливости называется то максимальное напряжение, которое может выдержать образец при данном числе циклов в условиях коррозионного воздействия. Предел коррозионной усталости является условной величиной, а не истинным пределом, так как металл при длительных выдержках разрушится и без знакопеременных напряжений, а лишь от одной коррозии. Поэтому предел коррозионной усталости обусловливают числом циклов знакопеременных нагрузок, которые при испытаниях выдерживают образец металла при данном напряжении, т. е. цифровые значения предела коррозионной усталости относят к определенной базе испытаний (числу циклов).  [c.106]

Нисходящий участок е/ диаграммы носит условный характер, поскольку действительная площадь поперечного сечения образца после образования шейки и первоначальная площадь, по которой определяют ординаты диаграммы, значительно отличаются друг от друга. Деля величину силы на действительную площадь поперечного сечения образца, можно получить значения истинных напряжений и построить соответствующую диаграмму (рис. 105, а — штриховая линия).  [c.99]

Для определения механических характеристик на практике используют условные диаграммы растяжения в координатах о — е. Построение диаграмм истинных напряжений значительно сложнее, и служат они главным образом целям теоретических исследований.  [c.100]

Так как истинная площадь поперечного сечения меньше первоначальной, то диаграмма истинных напряжений идет выше диаграммы условных напряжений, особенно после образования шейки, когда происходит резкое уменьшение поперечного сечения образца (кривая ОСЗ на рис. 11.8).  [c.35]

Расчез по напряжениям смятия условный, так как не учитывает истин-  [c.289]

Индикаторная диаграмма и диаграмма условных напряжений при растяжении и их характерные точки. Индикаторная диаграмма (рис. 56) отображает зависимость силы растяжения Р от абсолютного удлинения 1 = 1 — 1 , где I — текущая длина рабочей части образца, на которой определяется удлинение, Чтобы устранить масштабный фактор, строят диаграмму условных напряжений — зависимость условного напряжения Оуел = Р Р , где Fq == ndyA — начальная площадь поперечного сечения образца, от относительного удлинения е = Строят также диаграмму истинных напряжений (кривую упрочнения первого рода) зависимость истинного напряжения ст ст = — Р/Р от я, где F — текущая площадь поперечного сечения образца. Истинное напряжение называют еще сопротивлением металла деформации.  [c.155]

Рис. 5. Зависимость разрушающего напряжения от степени деформации для сплава МР47 (О) А — то же после отжига при 1570 К. оь — разрушающее напряжение, Еусд — условная деформация, Ецрт — истинная.

Этот результат находился в прямом противоречии с результатом, который Тэйлор и Квинни получили из эксперимента Геста. На основании эксперимента последнего они заключили, что гипотеза Максвелла — Мизеса хорошо описывает поверхность текучести для отожженной меди. Следует подчеркнуть, что в эксперименте Геста уровень начального нагружения, а отсюда и рассматриваемая поверхность текучести, произвольны, т. е. начальная пластическая деформация может быть того же порядка, что и пластическая деформация во втором эксперименте с непрерывным нагружением до большей деформации. Однако разгрузка и соответственно повторное нагружение по другим путям до вновь достигаемой поверхности текучести вызывают лишь малую деформацию, поэтому результаты были даны в долях условного напряжения и условной деформации. В противоположность этому в эксперименте второго типа Тэйлор и Квинни описали наблюдения в условных напряжениях и логарифмической (истинной) деформации. Следуя анализу Мора, Тэйлор и Квинни сравнили сдвиговую деформацию s при испытании на кручение с величиной lg(l+e), где е подобно s относится к исходным размерам образца.  [c.109]

Чтобы удостовериться, не был ли главным фактором сам цикл разгрузки и повторного нагружения, на что могли сослаться при выполнении исследования в прошлом веке, я пересчитал истинные напряжения и истинные деформации по данным Дорна, Голдберга и Титца на условные напряжения и условные деформации, пытаясь провести сравнение с общей параболической функцией отклика, соответствующей формуле (4.25) в разделе 4.21. Результаты (кружки) на плоскости —е на рис. 4.217 показывают, что единая функция отклика (соответствующие графики изображены сплошными линиями) не только описывает конечные деформации при наличии температурных изменений, но также и то, что после предварительной пластической деформации, разгрузки и повторного нагружения, сопровождаемого изменением температуры окружающей среды, изменения в функции отклика сводятся исключительно к смещению значения е ,, соответствующего вершине параболы в формуле  [c.323]

Напряжения, которыми оперируют в механических испытаниях, могут быть истинными и условными. Известно, что в процессе деформации величина площадки, на которой действуют напряжения (площадь сечения образца), меняется. Если эти изменеиия не учитывают и напряжение рассчитывают как отношение нагрузки в данный момент к исходной илощади сечения, то такое напряжение называют условным. Если же относят силу к величине фактического сечения в данный момент деформации, то получают истинное напряжение. Физический смысл имеют только истинные напряжения, однако на практике часто более удобно пользоваться условными. Это особенно оправдано при малой степени деформации, когда изменение площади сечения невелико.  [c.8]

Хотя условная диаграмма растяжения, получаемая непосредственно на испытательных машинах, имеет большое практическое значение, она все же не может полностью обеспечить надлежащего истолкования физической природы процессов деформации металлов и металлических сплавов. Поэтому при обработке результатов механических испытаний в исследовательских работах начинаютприменять так называемую истинную диаграмму растяжения, изображенную пунктирной кривой (фиг. 89). На ее горизонтальной оси откладываются изменения величины абсолютного удлинения Л/, а на вертикальной — 5 истинные напряжения. Истинное, или эффективное напряжение определяется как отношение нагрузки не к исходно площади поперечного сечения образца, а к площади, изменяющейся  [c.140]

Таким образом, для-определения силы Рг необходимо знать коэффициент усадки стружкп Кг и касательное напряжение т на условной плоскости сдвига. Коэффициент усадки стружки находят из опытов по резанию, а величину т можно получить на основании механических испытаний обрабатываемого материала на растяжение или сжатие. Связь между касательным напряжением т и истинным сдвигом е при механических испытаниях хорошо описывается поли-тропической зависимостью т Ле”. Если эту зависимость экстраполировать в область деформаций, свойственных процессу резания (рис. 171), то при е 2,5 касательные напряжения при механических испытаниях близки к касательным напряжениям при резании, и для определения касательного напряжения на условной плоскости сдвига можно пользоваться зависимостью х = А-2,5 . Экспериментальная проверка этого положения (рис. 172), проведенная для самых разнообразных материалов при различных условиях резания, дает удовлетворительные результаты. Обозначив А 2,5 ” = Ла.б, будем иметь  [c.220]

Сила Р, приложенная к некоторой площадке F, обычно не перпендикулярна к пей, а направлена под некоторым углом, поэтому в теле вояникают нормальные и касательные на-п р я ж е II и я (рис. 26, а). Напряжения могут быть 1) истинными — когда силу относят к сечению, существующему в данный момент ле( юрмацип 2) условными — когда силу относят к исходной  [c.42]

При этом методе оценка факторов неопределенности является условной. Например, в формуле (38) вызывает сомнение фактор /и стененн достоверности расчета. Численная оценка этого фактора по сути предполагает существование точного расчета, позволяющего определить истинную величину напряжений. Но тогда нет необ.чодпмости в поправочном коэффициенте, а достаточно ввести в расчет эти напряжения  [c.162]

Если растягивающую силу Р отнести к первоначальной площади сечения Fq. то получим так называемое условное напряжение oq PIFq. Соответственно относительная деформация ео может быть названа также условной. Зависимость между ао и еа называют условной диаграммой растяжения либо сжатия. Измерение истинной площади F не всегда удобно. Считая приближенно объем образца неизменным, получим = +ео), что позволяет вычислять истинное напряжение по формуле  [c.32]

---