Содержание:
- Формула
- Примеры нахождения орта вектора
Формула
Чтобы найти орт $bar{e}$ вектора
$bar{a}$, нужно вектор
$bar{a}$ поделить на его
длину:
$$bar{e}=frac{bar{a}}{|bar{a}|}$$
Если вектор задан на плоскости своими координатами
$bar{a}=left(a_{x} ; a_{y}right)$, то его орт вычисляется по формуле:
$$bar{e}=frac{bar{a}}{|bar{a}|}=frac{a_{x} cdot bar{i}+a_{y} cdot bar{j}}{sqrt{a_{x}^{2}+a_{y}^{2}}}=left(frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}}} ; frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}}}right)$$
Если вектор задан в пространстве и имеет координаты
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$, то его орт вычисляется по формуле:
$$bar{e}=frac{bar{a}}{|bar{a}|}=frac{a_{x} cdot bar{i}+a_{y} cdot bar{j}+a_{z} cdot bar{k}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}=$$
$$=left(frac{a_{x}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} ; frac{a_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}} ; frac{a_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}right)$$
Примеры нахождения орта вектора
Пример
Задание. На плоскости задан вектор
$bar{a}=(-2 ; 2)$ . Найти его орт.
Решение. Для нахождения орта заданного вектора воспользуемся формулой:
$$bar{e}=frac{bar{a}}{|bar{a}|}=frac{a_{x} cdot bar{i}+a_{y} cdot bar{j}}{sqrt{a_{x}^{2}+a_{y}^{2}}}$$
Подставляя заданные координаты, получим:
$$bar{e}=frac{-2 cdot bar{i}+2 cdot bar{j}}{sqrt{(-2)^{2}+2^{2}}}=frac{-2 cdot bar{i}+2 cdot bar{j}}{sqrt{4+4}}=frac{-2 cdot bar{i}+2 cdot bar{j}}{sqrt{8}}=$$
$$=frac{-2 cdot bar{i}+2 cdot bar{j}}{2 sqrt{2}}=-frac{1}{sqrt{2}} cdot bar{i}+frac{1}{sqrt{2}} cdot bar{j}$$
Таким образом, искомый орт вектора $bar{a}$
имеет координаты $bar{e}=left(-frac{1}{sqrt{2}} ; frac{1}{sqrt{2}}right)$
Ответ. $bar{e}=left(-frac{1}{sqrt{2}} ; frac{1}{sqrt{2}}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Даны точки
$A(3 ;-1 ; 4)$ и $B(2 ; 0 ; 2)$ . Найти орт вектора
$overline{A B}$
Решение. Найдем координаты вектора
$overline{A B}$, для этого из координат конца вектора (точки
$B$ ) вычтем соответствующие координаты начала (точки
$A$ ):
$$overline{A B}=(2-3 ; 0-(-1) ; 2-4)=(-1 ; 1 ;-2)$$
Для нахождения орта полученного вектора воспользуемся формулой
$$bar{e}=frac{a_{x} cdot bar{i}+a_{y} cdot bar{j}+a_{z} cdot bar{k}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}$$
Подставим в неё координаты вектора $overline{A B}$, будем иметь:
$$bar{e}=frac{-1 cdot bar{i}+1 cdot bar{j}-2 cdot bar{k}}{sqrt{(-1)^{2}+1^{2}+(-2)^{2}}}=frac{-1 cdot bar{i}+1 cdot bar{j}-2 cdot bar{k}}{sqrt{1+1+4}}=$$
$$=frac{-1 cdot bar{i}+1 cdot bar{j}-2 cdot bar{k}}{sqrt{6}}=-frac{1}{sqrt{6}} cdot bar{i}+frac{1}{sqrt{6}} cdot bar{j}-frac{2}{sqrt{6}} cdot bar{k}$$
Таким образом, орт вектора $overline{A B}$ имеет координаты $bar{e}=left(-frac{1}{sqrt{6}} ; frac{1}{sqrt{6}} ;-frac{2}{sqrt{6}}right)$
Ответ. $bar{e}=left(-frac{1}{sqrt{6}} ; frac{1}{sqrt{6}} ;-frac{2}{sqrt{6}}right)$
Читать дальше: как найти вектор по точкам.
Единичный вектор
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
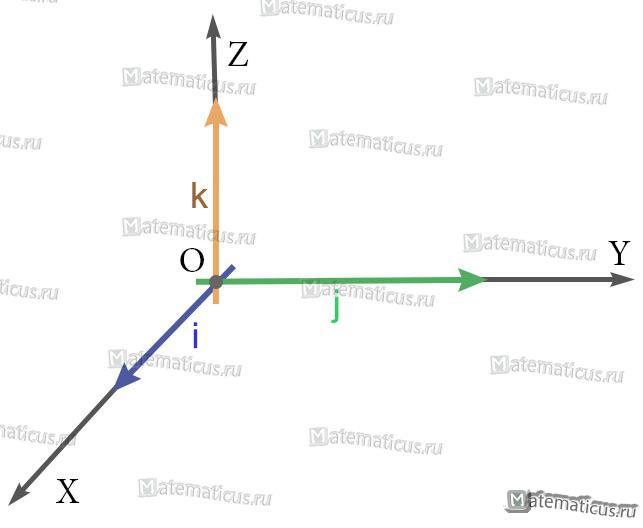
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0), j(0;1;0), k(0;0;1)
Единичные векторы являются некомпланарными.
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
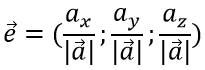
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Находим длину вектора a
затем вычисляем единичный вектор e
Векторное произведения единичных векторов
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус» . Смотрите схему 1.
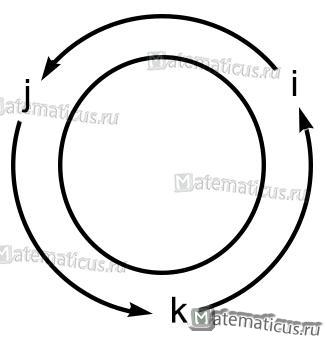
На основании схемы получаем таблицу векторного произведения единичных векторов
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
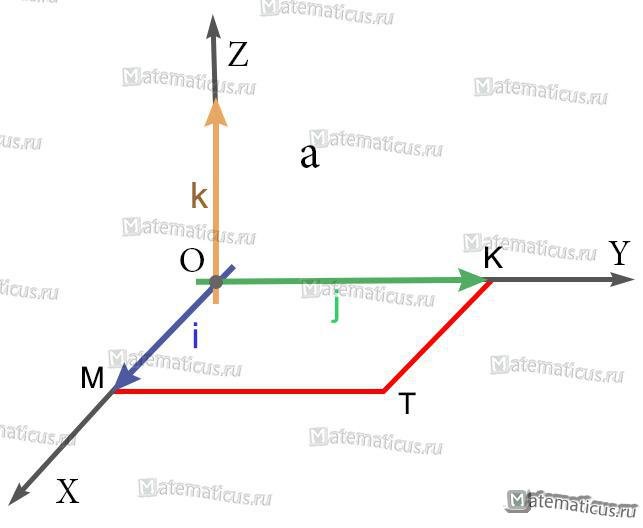
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.5 / 5. Количество оценок: 4
Что такое орты
Орт:
- это вектор,
- он лежит на оси,
- направлен туда же, куда направлена ось,
- его длина равна единице.
На рисунке 1 изображены орты для двумерного а) и трехмерного б) случаев.

Орты сонаправлены с осями, на которых они лежат:
- Орт ( vec ) направлен вдоль оси Ox;
- Орт ( vec ) направлен вдоль оси Oy;
- Орт ( vec ) направлен вдоль оси Oz;
Орты обладают единичной длиной:
Все три орта взаимно перпендикулярны. Перпендикулярные векторы часто называют ортогональными.
Любые два орта из трех, лежат в одной плоскости:
- Орты ( vec ) и ( vec ) лежат в плоскости xOy;
- Орты ( vec ) и ( vec ) лежат в плоскости xOz;
- Орты ( vec ) и ( vec ) лежат в плоскости yOz;
Векторы, лежащие в одной плоскости, называют компланарными. Об этом подробно написано «здесь» (откроется в новой вкладке).
Координаты вектора можно указать двумя способами. Либо, перечислив эти координаты в скобках, либо, с помощью разложения вектора по ортам.
Как найти орт вектора
Формула
Примеры нахождения орта вектора
Задание. На плоскости задан вектор $bar=(-2 ; 2)$ . Найти его орт.
Решение. Для нахождения орта заданного вектора воспользуемся формулой:
Подставляя заданные координаты, получим:

Задание. Даны точки $A(3 ;-1 ; 4)$ и $B(2 ; 0 ; 2)$ . Найти орт вектора $overline$
Решение. Найдем координаты вектора $overline$, для этого из координат конца вектора (точки $B$ ) вычтем соответствующие координаты начала (точки $A$ ):
Для нахождения орта полученного вектора воспользуемся формулой
Подставим в неё координаты вектора $overline$, будем иметь:
Таким образом, орт вектора $overline$ имеет координаты $bar=left(-frac<1><sqrt<6>> ; frac<1><sqrt<6>> ;-frac<2><sqrt<6>>right)$
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_13_15.php
[/spoiler]
Как найти орт вектора
Вектором в геометрии называют направленный отрезок или упорядоченную пару точек евклидова пространства.Ортом вектора является единичный вектор нормированного векторного пространства или вектор, норма (длина) которого равна единице.

Вам понадобится
- Знания по геометрии.
Инструкция
Для начала необходимо вычислить длину вектора. Как известно, длина (модуль) вектора равна корню квадратному из суммы квадратов координат. Пусть дан вектор с координатами: a(3, 4). Тогда его длина равна |a| = (9 + 16)^1/2 или |a|=5.
Чтобы найти орт вектора a, необходимо поделить каждую его который называется ортом или единичным вектором. Для вектора а(3, 4) ортом будет являться вектор а(3/5, 4/5). Вектор a’ будет являться единичным для вектора а.
Для проверки, правильно ли найден орт, можно проделать следующее: найти длину полученного орта, если она равна единице, то все найдено верно, если нет, то в расчеты закралась ошибка. Проверим правильно ли найден орт a’. Длина вектора a’ равна: a’ = (9/25 + 16/25)^1/2 = (25/25)^1/2 = 1. Итак, длина вектора a’ равна единице, значит орт найден верно.
Видео по теме
Обратите внимание
Орт нулевого вектора не существует, так как длина нулевого вектора равна нулю.
Полезный совет
Для того, чтобы понять единичный ли вектор, необходимо найти его длину. Если она равна единице, то вектор единичный.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Два единичных вектора на плоскости
Единичный вектор, или орт[1], — вектор нормированного пространства, длина которого равна единице. Единичные вектора используются, в частности, для задания направлений в пространстве. Множество единичных векторов образует единичную сферу.
Единичный вектор часто обозначается строчной буквой с крышкой: 
Единичный вектор 

где 

В качестве базисных часто выбираются именно единичные векторы, так как это упрощает вычисления. Такие базисы называют нормированными. В том случае, если эти векторы также ортогональны, такой базис называется ортонормированным базисом.
См. также[править | править код]
- Единичный отрезок
Примечания[править | править код]
- ↑ Большая советская энциклопедия
Орт:
- это вектор,
- он лежит на оси,
- направлен туда же, куда направлена ось,
- его длина равна единице.
На рисунке 1 изображены орты для двумерного а) и трехмерного б) случаев.

Рис. 1. Единичные векторы – орты, располагаются на осях координат
Орты сонаправлены с осями, на которых они лежат:
- Орт ( vec{i} ) направлен вдоль оси Ox;
- Орт ( vec{j} ) направлен вдоль оси Oy;
- Орт ( vec{k} ) направлен вдоль оси Oz;
Орты обладают единичной длиной:
[ |vec{i}| = |vec{j}| = |vec{k}| = 1]
Все три орта взаимно перпендикулярны. Перпендикулярные векторы часто называют ортогональными.
Любые два орта из трех, лежат в одной плоскости:
- Орты ( vec{i} ) и ( vec{j} ) лежат в плоскости xOy;
- Орты ( vec{i} ) и ( vec{k} ) лежат в плоскости xOz;
- Орты ( vec{j} ) и ( vec{k} ) лежат в плоскости yOz;
Векторы, лежащие в одной плоскости, называют компланарными. Об этом подробно написано «здесь» (откроется в новой вкладке).
Координаты вектора можно указать двумя способами. Либо, перечислив эти координаты в скобках, либо, с помощью разложения вектора по ортам.
Пример:
Сравните два способа обозначения вектора
[ vec{a} = left{ -2; 7; -5 right} ]
и
[vec{a} = -2 cdot vec{i} + 7cdot vec{j} – 5 cdot vec{k} ]

