Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 декабря 2015 года; проверки требуют 66 правок.
У этого термина существуют и другие значения, см. Решётка.
Очень большая отражательная дифракционная решётка.
Дифракционная решётка — оптический прибор, действие которого основано на использовании явления дифракции света. Представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность.
История[править | править код]
Первое описание явления сделал в 1673 году Джеймс Грегори, который наблюдал дифракцию на птичьих перьях:
Если вы сочтёте нужным, вы можете показать мистеру Ньютону небольшой эксперимент, который (если он еще не знает об этом) будет достоин его внимания. Впустите солнечный свет через маленькое отверстие в затемнённый дом, а в отверстие поместите перо (чем тоньше и белее, тем лучше для этой цели), и оно направит на белую стену или бумагу напротив нее ряд маленьких кругов и овалов (если я их не ошибаюсь), из которых один белый (а именно середина, которая противоположна Солнцу), а все остальные по-разному окрашены. Я с радостью выслушаю его мысли об этом.[1]
Дэвид Риттенхаус в 1786 году впервые изготовил дифракционную решётку и измерил углы отклонения для разных цветов[2].
В 1801 году Томас Юнг открыл и объяснил интерференцию света. В 1818 году Огюстен Жан Френель разработал теорию дифракции света.
Опираясь на представления Юнга и Френеля о световых волнах, Йозеф Фраунгофер в 1821 году впервые использовал дифракционную решётку (которую он и изготовил) для получения спектров и вычисления длин волн.
Виды решёток[править | править код]
- Отражательные — Штрихи нанесены на зеркальную (металлическую) поверхность, и наблюдение ведется в отражённом свете
- Прозрачные — Штрихи нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном экране), наблюдение ведется в проходящем свете.
Описание явления[править | править код]
Так выглядит свет лампы накаливания фонарика, прошедший через прозрачную дифракционную решётку. Нулевой максимум (m=0) соответствует свету, прошедшему сквозь решётку без отклонений. В силу дисперсии решётки в первом (m=±1) максимуме можно наблюдать разложение света в спектр. Угол отклонения возрастает с ростом длины волны (от фиолетового цвета к красному)
Идеализированная решетка состоит из набора щелей с периодом d, который должен быть больше, чем длина волны, представляющая интерес, чтобы вызвать дифракцию. Пусть на решетку нормально(перпендикулярно решетке) падает плоская волна монохроматического света с длиной волны 
, тогда каждая щель в решетке действует как квазиточечный источник, из которого свет распространяется во всех направлениях согласно с принципом Гюйгенса — Френеля. Происходит интерференция света, излученного всеми щелями, при этом если в каком-то направлении свет от двух соседних щелей оказывается в одинаковой фазе, происходит конструктивная интерференция, и в этом направлении появляется максимум. Так как для разных длин волн максимумы интерференции оказываются под разными углами (определяемыми разностью хода интерферирующих лучей), то белый свет раскладывается в спектр.
Формулы[править | править код]
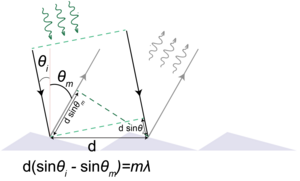
Иллюстрация к нахождению условия максимума при отражении от дифракционной решетки при наклонном падении.
Иллюстрация к нахождению порядков дифракции.
Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d.
Если известно число штрихов (
), приходящихся на 1 мм решётки, то период решётки находят по формуле: 
мм.
При нормальном падении плоской волны условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид:
где
— период решётки,- — угол максимума данного цвета,
- — порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки,
- — длина волны.
Это условие может быть выведено исходя из того, что разность фаз между лучами, отраженными от поверхностей на расстоянии, равном периоду решетки, должна быть кратна 
, или, другими словами, разность оптических путей кратна длине волны. При этом положение максимумов зависит только от периода решетки, а ширина щели или форма штрихов влияет на плавную огибающую функции максимумов.
Если же свет падает на решётку под углом 
, то:
Эта формула может быть проиллюстрирована графически, для того, чтобы найти направление на какой-то порядок дифракции, необходимо нарисовать окружность с радиусом, равным периоду решетки, умноженному на показатель преломления вещества, в котором наблюдаются порядки. Затем через конец прошедшего или отражённого луча необходимо провести вертикальную прямую. После этого, необходимо провести еще несколько вертикальных прямых на расстоянии друг от друга, равным длине волны. Направления на порядки дифракции будут из центра окружности в точки, где она пересекается с вертикальными прямыми. Фактически, такая иллюстрация аналогична построению Эвальда в одномерном случае.
Характеристики[править | править код]
Одной из характеристик дифракционной решётки является угловая дисперсия. Предположим, что максимум какого-либо порядка наблюдается под углом 
для длины волны λ и под углом +Δ — для длины волны λ+Δλ. Угловой дисперсией решётки называется отношение D=Δ/Δλ. Выражение для D можно получить, если продифференцировать формулу дифракционной решётки
Таким образом, угловая дисперсия увеличивается с уменьшением периода решётки d и возрастанием порядка спектра m.
Вторая характеристика дифракционной решетки — разрешающая способность. Она обусловлена угловой шириной главного максимума и определяет возможность раздельного наблюдения 2 близких спектральных линий. При увеличении порядка спектра m возрастает
Также существует еще одна характеристика дифракционной решетки — дисперсионная область. Она определяет для каждого порядка спектральный диапазон от перекрытия спектров. Данный параметр обратно-пропорционален порядку спектра m
Изготовление[править | править код]
Хорошие решётки требуют очень высокой точности изготовления. Если хоть одна щель из множества будет нанесена с ошибкой, то решётка будет бракована. Машина для изготовления решёток прочно и глубоко встраивается в специальный фундамент. Перед началом непосредственного изготовления решёток, машина работает 5—20 часов на холостом ходу для стабилизации всех своих узлов. Нарезание решётки длится до 7 суток, хотя время нанесения штриха составляет 2—3 секунды.
Применение[править | править код]
Дифракционную решётку применяют в спектральных приборах, также в качестве оптических датчиков линейных и угловых перемещений (измерительные дифракционные решётки).
Дифракция на примере одной щели
Примеры[править | править код]
Дифракция на компакт-диске
Один из простейших и распространённых в быту примеров отражательных дифракционных решёток — компакт-диск. На поверхности компакт-диска — дорожка в виде спирали с шагом 1,6 мкм между витками. Примерно треть ширины (0,5 мкм) этой дорожки занята углублением (это записанные данные), рассеивающим падающий на него свет, примерно две трети (1,1 мкм) — нетронутая подложка, отражающая свет. Таким образом, компакт-диск — отражательная дифракционная решётка с периодом 1,6 мкм. Кроме того, такой же отражательной дифракционной решёткой является и пустой CD-R диск, и пустой DVD диск, поскольку на них имеется спиральная дорожка для направления луча лазера при записи информации. Причём период решётки для DVD — 0,74 мкм.
См. также[править | править код]
Видеоурок: дифракционная решетка
- Дифракция на N щелях
- Дифракция Фраунгофера
- Дифракция Френеля
- Интерференция света
- Фурье-оптика
- Оптическая решётка
- Призма (оптика)
Примечания[править | править код]
- ↑ Letter from James Gregory to John Collins, dated 13 May 1673. Reprinted in: Correspondence of Scientific Men of the Seventeenth Century…., ed. Stephen Jordan Rigaud (Oxford, England: Oxford University Press, 1841), vol. 2, page 254. Books.Google.com Архивная копия от 16 сентября 2020 на Wayback Machine.
- ↑ И. Д. Багбая. К истории дифракционной решётки. Успехи физических наук, т. 108, вып. 2, октябрь 1972. стр. 335-337.. Дата обращения: 21 августа 2020. Архивировано 12 августа 2017 года.
Литература[править | править код]
- Эшелетты // Элоквенция — Яя. — М. : Советская энциклопедия, 1957. — С. 293. — (Большая советская энциклопедия : [в 51 т.] / гл. ред. Б. А. Введенский ; 1949—1958, т. 49).
- Ландсберг Г. С. Оптика, 1976
- Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
- Тарасов К. И. Спектральные приборы, 1968
Ссылки[править | править код]
- Экспериментальное определение периода решётки у компакт-диска — видео с пояснениями на английском языке
Период дифракционной решетки
4.2
Средняя оценка: 4.2
Всего получено оценок: 169.
4.2
Средняя оценка: 4.2
Всего получено оценок: 169.
Для измерения длины световой волны нередко используется специальный оптический прибор, который называется дифракционной решеткой. Важнейшей характеристикой любой дифракционной решетки является ее период. Рассмотрим эту характеристику подробнее.
Дифракция на тонкой щели
Основой работы дифракционной решетки является способность световых волн к дифракции на тонких узких щелях. Дифракционная картина на одной узкой щели представляет собой чередование максимумов и минимумов освещенности, причем главный максимум имеет наибольшую интенсивность, а на остальных максимумах интенсивность освещенности быстро падает.
Если взять две тонких щели, расположенные рядом, то волны от щелей начинают интерферировать между собой, давая на дифракционной картине дополнительные минимумы, основные же максимумы становятся выражены более четко. При трех щелях дополнительных минимумов становится больше, а основные максимумы выделяют еще лучше.
Если взять большое количество периодических тонких щелей, в результате получаем дифракционную решетку.
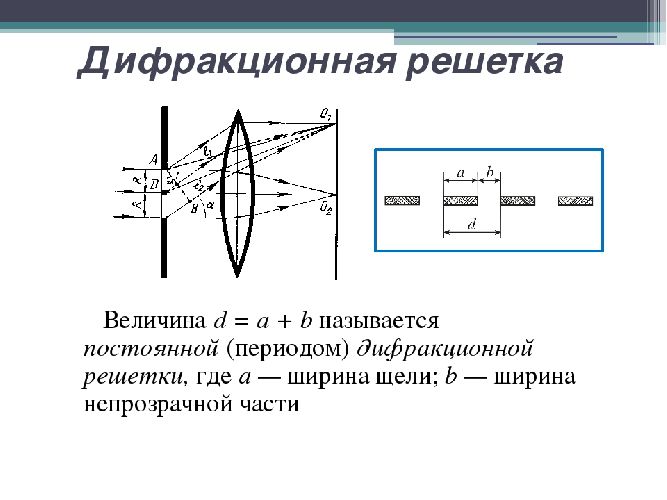
Дифракционная решетка
Измерительная дифракционная решетка имеет, как правило, несколько тысяч штрихов на миллиметр, общее количество штрихов доходит до сотен тысяч. Дифракционная решетка может быть прозрачной или отражающей. В прозрачной решетке чередуются прозрачные и непрозрачные участки. В отражающей чередуются отражающие и неотражающие участки.
Расстояние между центрами соседних штрихов $d$ называется периодом дифракционной решетки и является важнейшей ее характеристикой. Формула периода дифракционной решетки:
$$d = S_{щели}+ S_{непрозр}$$
То есть период дифракционной решетки равен сумме ширины щели и ширине непрозрачной области между соседними щелями.
Если число щелей в решетке обозначить через $N$, то в создании интерференционной картины за решеткой участвует $N$ когерентных световых пучков. Положение главных максимумов определяется условием:
$$d sin varphi = k lambda$$
где:
- $varphi$ — угол отклонения для данного максимума;
- $lambda $ — длина волны света;
- $k$ — 0,1,2… — номер максимума.
Между главными максимумами на дифракционной картине имеется $N-1$ минимумов, максимумы же имеют интенсивность во столько же раз больше (по сравнению с дифракцией на одиночной щели).
Наиболее интенсивным остается центральный максимум ($k=0$). Кроме того, поскольку угол отклонения зависит от длины волны, дифракционная решетка разлагает белый свет в спектр.
Измерение длины волны с помощью дифракционной решетки
Дифракционная решетка позволяет очень точно определять длину волны падающего пучка. Для этого достаточно измерить угол $varphi$ отклонения, который соответствует некоторому максимуму.
При этом важным параметром является разрешающая способность дифракционной решетки $R$. Разрешающая способность прямо пропорциональна количеству штрихов и порядку максимума:
$$R=kN$$
Разрешающая способность показывает, во сколько раз длина волны больше абсолютной погрешности ее определения.
Что мы узнали?
Дифракционная решетка — это совокупность непрозрачных штрихов и прозрачных участков. Период дифракционной решетки — это сумма ширины прозрачного участка и ширины штриха. Дифракционная решетка применяется для измерения длины волны падающего света. Важнейшими параметрами дифракционной решетки является период и разрешающая способность.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 169.
А какая ваша оценка?
Простейшее измерительное устройство на рисунке ниже состоит из двух линеек, на одной из которых закреплена дифракционная решётка, а над второй возвышается узкая щель, например, из двух лезвий. Используются расстояния в миллиметрах от дифракционной решётки до линейки с щелью, и от щели (максимума нулевого порядка) до максимума первого порядка.
Нужно смотреть через дифракционную решётку на источник света с известной длиной волны: лазер (важно следить, чтобы свет лазера гарантированно не мог повредить глаза: снижать яркость узкой щелью, отражением, светорассеивателем) или пламя горелки, окрашенное в жёлтый цвет двумя линиями 588,995 и 589,5924 нм с помощью проволоки, покрытой раствором соли NaCl и внесённой в огонь. Также подойдёт турбо зажигалка с красным пламенем, дающим в спектре тонкую линию 670,78 нм. Скорее всего в ней используется пластина с веществом, содержащим литий. Если кто знает подобную информацию о зажигалке с зелёным пламенем, то напишите, пожалуйста, комментарий.
Период дифракционной решётки можно посчитать следующим образом:
589нм*204мм/20мм≈6000 нм
Этим же устройством можно определить длину волны света, зная период дифракционной решётки:
20*6000/204≈588 нм.
Существует и немного другой вариант устройства. Лазер светит через дифракционную решётку на линейку. В этом случае щель не нужна.
Им тоже можно определить характеристику дифракционной решётки и света, но только с помощью лазеров.
Период решётки: 780нм*250мм/32,5мм=6000 нм
Длина волны: 32,5мм*6000нм/250мм=780 нм
Я использовал дифракционную решётку из насадки “Звёздное небо”, которая шла в комплекте с лазерной указкой. Там две решётки. Насадку нужно разобрать и вытащить одна решётку. Дифракционная решётка из CD даёт ошибку в 100 нм и не подходит.
Готовую фотографию спектра минимум с двумя известными линиями можно сопоставить в Photoshop со шкалой, чтобы узнать длины волн неизвестных линий.
Создаём чистый лист, вставляем на него шкалу и изображение, на котором есть неизвестные длины волн. Для сопоставления известных длин волн со шкалой, изменяем масштаб фотографии таким образом: нажимаем “Редактирование”, “Трансформирование”, “Масштабирование”; нажимаем кнопку “Сохраняет пропорции” и меняем числовые значения вверху, указанные в %. После сопоставления, неизвестные длины волн автоматически займут правильные положения на шкале. Должно получится примерно следующее:
Известные линии спектров газоразрядных ламп есть в ГОСТ Р 55703-2013. Некоторые спектры в виде графиков и в виде фотографий.
Можно использовать и математический метод. Например, нужно узнать длину волны лазера с фотографии выше. Открываем её в Photoshop CC. С помощью инструмента “Линейка” измеряем расстояние от линии натрия до линии лития. Оно равно 1223 п. Измеряем расстояние от натрия до лазера – 1104 п. Считаем таким образом: (670нм-589нм)/1223п*1104п+589нм=662 нм
Если у нас фотография с источником излучения, полученная простейшим спектроскопом, то неизвестную линию считаем так.
Узнаём линию 1064 нм. Измеряем расстояние от точки лазера до линии 802 нм. Будет 2876 п. От лазера до неизвестной линии – 3831 п. 802нм*3831п/2876п=1068 нм
Обновляемая тематическая подборка статей моего канала здесь.
Спасибо за то, что дочитали мою статью!
Если информация понравилась, ставьте лайк. Также буду рад комментариям!
Дифракционная
решётка —
оптический прибор, работающий по
принципу дифракции света,
представляет собой совокупность большого
числа регулярно расположенных штрихов
(щелей, выступов), нанесённых на некоторую
поверхность.
Виды
решёток
-
Отражательные:
Штрихи нанесены на зеркальную
(металлическую) поверхность, и наблюдение
ведется в отражённом свете -
Прозрачные:
Штрихи нанесены на прозрачную поверхность
(или вырезаются в виде щелей на
непрозрачном экране), наблюдение ведется
в проходящем свете.
Формулы
Расстояние,
через которое повторяются штрихи на
решётке, называют периодом дифракционной
решётки. Обозначают буквой d.
Если
известно число штрихов (N),
приходящихся на 1 мм решётки, то период
решётки находят по формуле: d =
1 / N мм.
Условия
интерференционных максимумов дифракционной
решётки, наблюдаемых под определёнными
углами, имеют вид:
где
d —
период решётки,
α —
угол максимума данного цвета,
k —
порядок максимума, то есть порядковый
номер максимума, отсчитанный от центра
картинки,
λ —
длина волны.
Дифракционная
решетка
Д
ифракция
на решетке происходит аналогично
дифракции на щели. Однако при большом
числе близко расположенных параллельных
щелей дифракционные максимумы значительно
сужаются. Расстояние между
соответствующими точками соседних
щелей (или сумма ширины щели и промежутка
между щелями) называется постоянной,
или
периодом g
дифракционной
решетки. У хороших дифракционных решеток
число щелей на 1 мм достигает 1700.’
Если
α
макс — угол, определяющий направление
на дифракционный ‘ максимум,
g
—
постоянная решетки,
— длина волны,
/
— расстояние от решетки до экрана,
а
—
расстояние до максимума к-го порядка,
то
в
соответствии
с рисунком
где
а
определяется
из условия tg
а
=
а/1.
Обратите
внимание:
1Синус
дифракционного угла пропорционален
длине волны. Поэтому решетка в отличие
от призмы преломляет красный свет
сильнее
всего.
2
чем меньше постоянная решетки тем больше
угол дифракции при фиксированной длинны
волны
3
если постоянная дифракционной решетки
известна то по положению дифракционных
максимумов можно определить длину волны
света.
Уравнение,
описывающее дифракцию на решетке, можно
записать в виде:
m =
d
( sin
ф
)
m-порядок
спектра
d-период
решётки
Для
того, чтобы в точке наблюдался
интерференционный максимум, разность
хода Δ между волнами, испущенными
соседними щелями, должна быть равна
целому числу длин волн:
|
Здесь d –
период решетки, m –
целое число, которое называется порядком
дифракционного максимума.
В тех точках экрана, для которых это
условие выполнено, располагаются так
называемые главные
максимумы дифракционной
картины.
В
фокальной плоскости линзы расстояние ym от
максимума нулевого порядка (m = 0)
до максимума m-го
порядка при малых углах дифракции равно
|
|
где F –
фокусное расстояние.
В
оптическом диапазоне вследствие малости
длины волны размер зон Френеля оказывается
достаточно малым. Дифракционные явления
проявляются наиболее отчетливо, когда
на препятствии укладывается лишь
небольшое число зон:
|
|
Это
соотношение можно рассматривать
как критерий
наблюдения дифракции.
Если число зон Френеля, укладывающихся
на препятствии, становится очень большим,
дифракционные явления практически
незаметны:
|
|
Это
сильное неравенство определяет границу
применимости геометрической оптики.
Узкий пучок света, который в геометрической
оптике называется лучом, может быть
сформирован только при выполнении этого
условия. Таким образом, геометрическая
оптика является предельным случаем
волновой оптики.
34.
Поляризация
света – процесс упорядочения колебаний
вектора напряжённости электрического
поля световой волны при прохождении
света сквозь некоторые вещества (при
преломлении) или при отражении светового
потока.
Поляризатор
– вещество (или устройство) служащее
для преобразования естественного света
в плоскополяризованный.
Плоскость
поляризации – плоскость, проходящая
через направление колебаний светового
вектора плоскополяризованной волны и
направление распространения этой волны.
35.
Процессы
получения и преобразования поляризов.
света основаны на взаимодействиях света
с веществом, нарушающих осевую симметрию
светового луча. Для получения полностью
или частично поляризованного света
используется одно из трёх физ. явлений:
поляризация при отражении или преломлении
света на границе раздела двух изотропных
сред с разл. показателями преломления,
линейный дихроизм и двойное лучепреломление
.В первом случае анизотропия взаимодействия
света со средой определяется наличием
выделенной плоскости падения света и
различием коэф. отражения для компонент
светового луча, поляризованных параллельно
и перпендикулярно этой плоскости.
При
нормальном падении света на поверхность
раздела (когда положение плоскости
падения не определено) аксиальная
симметрия взаимодействия света со
средой не нарушается и поляризац.
преобразования светового пучка не
происходит. В соответствии с ф-лами
Френеля степень поляризации отражённой
и преломлённой компонент светового
пучка зависит от угла падения. Если
световой луч падает на границу раздела
под углом Брюстера (см. Брюстера закон),
то отражённый свет оказывается полностью
поляризованным. На этом основано действие
отражательных П. Осн. недостаток отражат.
П.- малость коэф. отражения – устраняется
при использовании многослойных
диэлектрич. покрытий (интерференционные
П.). Однако при этом сохраняются общие
для всех отражат. П. недостатки – сильная
зависимость степени поляризации от
угла падения (малая угл. апертура) и от
длины волны света (хроматизм).
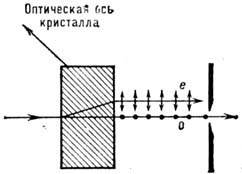
Рис.
Поляризация света с помощью двупреломляю-щего
кристалла: направления электрических
колебаний указаны стрелками (колебания
в плоскости рисунка) и точками
(перпендикулярно плоскости рисунка); о
и е – обыкновенный и необыкновенный
лучи.
36
. Закон
Брюстера — закон оптики, выражающий
связь показателя преломления с таким
углом, при котором свет, отражённый от
границы раздела, будет полностью
поляризованным в плоскости, перпендикулярной
плоскости падения, а преломлённый луч
частично поляризуется в плоскости
падения, причем поляризация преломленного
луча достигает наибольшего значения.
Легко установить, что в этом случае
отраженный и преломленный лучи взаимно
перпендикулярны. Соответствующий угол
называется углом Брюстера.
Это
явление оптики названо по имени
шотландского физика Дэвида Брюстера,
открывшего его в 1815 году.
Закон
Брюстера: , где n21 — показатель преломления
второй среды относительно первой, θBr —
угол падения (угол Брюстера).
При
отражении от одной пластинки под углом
Брюстера интенсивность линейно
поляризованного света очень мала (около
4 % от интенсивности падающего луча).
Поэтому для того, чтобы увеличить
интенсивность отраженного света (или
поляризовать свет, прошедший в стекло,
в плоскости, параллельной плоскости
падения) применяют несколько скрепленных
пластинок, сложенных в стопу — стопу
Столетова. Легко проследить по чертежу
происходящее. Пусть на верхнюю часть
стопы падает луч света. От первой пластины
будет отражаться полностью поляризованный
луч (около 4 % первоначальной интенсивности),
от второй пластины также отразится
полностью поляризованный луч (около
3,75 % первоначальной интенсивности) и
так далее. При этом луч, выходящий из
стопы снизу, будет все больше поляризоваться
в плоскости, параллельной плоскости
падения, по мере добавления пластин.
37.
Поляриза́тор — вещество, позволяющее
выделить из электромагнитной волны
(естественный свет является частным
случаем) часть, обладающую желаемой
поляризацией при пропускании его сквозь
или отражении от поверхности, получая
проекцию волны на плоскость поляризации.
Они используются в поляризацио́нных
фильтрах. В радиотехнике и в быту под
поляризатором понимается устройство
для преобразования вертикальной или
горизонтальной поляризации в круговую
(эллиптическую) или наоборот. В антеннах
в качестве поляризаторов используют
волноводы с вкрученными винтами.
Поляроид
— название синтетической пластиковой
плёнки, используемой для поляризации
света. Обычный свет превращается в
плоскополяризированный, проходя через
пластинки, сделанные из материала,
называемого поляроидом, или через
кристаллы кальцита (особая кристаллическая
форма CaCO3), расположенные таким образом,
что они образуют так называемую призму
Николя.
Пусть
на поляризатор (или анализатор) падает
линейно поляризованный свет с амплитудой
Е0. Амплитуда прошедшего света будет
равна Е=Е0сosj, а интенсивность I=I0сos2j.
Эта
формула выражает закон Малюса:
Интенсивность
линейно поляризованного света, прошедшего
анализатор, пропорциональна квадрату
косинуса угла j между плоскостью колебаний
падающего света и плоскостью анализатора.
38.
ФРЕНЕЛЯ
ФОРМУЛЫ – определяют отношения амплитуды,
фазы и состояния поляризации отражённой
и преломлённой световых волн, возникающих
при прохождении света через границу
раздела двух прозрачных диэлектриков,
к соответствующим характеристикам
падающей волны. Установлены О. Ж. Френелем
в 1823 на основе представлений об упругих
поперечных колебаниях эфира. Однако те
же самые соотношения – Ф. ф.- следуют в
результате строгого вывода из эл–магн.
теории света при решении ур-ний Максвелла.
39.
При падении на плоскую границу различают
две поляризации света. s-Поляризация —
это поляризация света, для которой
напряжённость электрического поля
электромагнитной волны перпендикулярна
плоскости падения (т.е. плоскости, в
которой лежат и падающий, и отражённый
луч). p-Поляризация — поляризация света,
для которой вектор напряжённости
электрического поля лежит в плоскости
падения.
Формулы
Френеля для s-поляризации и p-поляризации
различаются. Поскольку свет с разными
поляризациями по-разному отражается
от поверхности, то отражённый свет
всегда частично поляризован, даже если
падающий свет неполяризован. Угол
падения, при котором отражённый луч
полностью поляризован, называется углом
Брюстера; он зависит от отношения
показателей преломления сред, образующих
границу раздела.
40.
Нормальное
падение
При
нормальном падении
Тогда коэффициент отражения определяется
так:
(3.3.1)
Исходя
из выражения ( 3.2.12), получим коэффициент
пропускания:
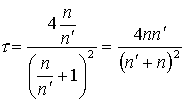
(3.3.2)
Если
граница раздела сред – стекло-воздух,
то ,
то есть при нормальном падении света
на стекло отражается около 4% энергии.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов) , нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.
Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d.
Если известно число штрихов (N), приходящихся на 1 мм решётки, то период решётки находят по формуле: d = 1 / N мм.
Условия интерфереционных максимумов дифракционной решётки, наблюдаемых под определенными углами, имеют вид:
dsinα = k λ
где
d — период решётки,
α — угол максимума данного цвета,
k — порядок максимума,
λ — длина волны.
Если же свет падает на решетку под углом θ, то:
d{sinα – sinθ} = k λ
