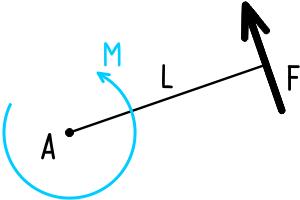
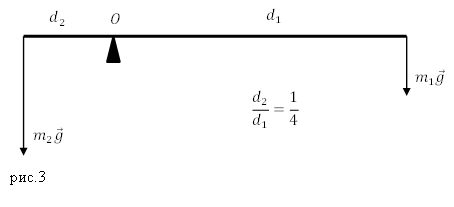Плечо силы — кратчайшее расстояние между линией действия силы и связанной с ней точкой (полюсом или осью вращения) при создании силой момента.
Определяется длинной нормали (перпендикуляра) к линии усилия проведенной из рассматриваемой точки.
Обозначается: L, l или h. Измеряется в метрах [м].
Плечо силы – один из двух множителей определяющих момент силы.
Наш короткий видеоурок про момент и плечо силы с примерами:
Другие видео
О плече силы можно говорить только тогда, когда есть прямая связь между силой и точкой относительно которой возникает момент.
Порядок нахождения плеча силы
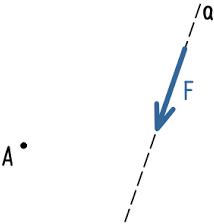
Рассмотрим порядок нахождения плеча силы F относительно точки A.
Для этого покажем прямую a, по направлению действия силы F
Из точки A опустим перпендикуляр к прямой a.
Длина этого перпендикуляра является плечом силы.
Примеры определения плеча силы
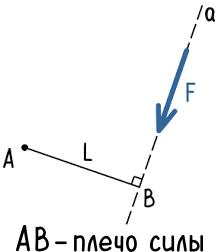
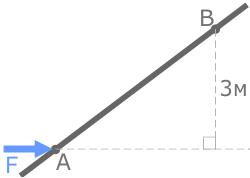
- Сила расположена перпендикулярно оси стержня и известно расстояние между точками A и B.
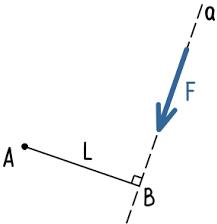
Плечо силы относительно точки A равно длине отрезка AB. - Сила расположена под определенным углом к оси стержня
Плечо силы относительно точки B составляет AB×cos30° - Известно расстояние от точки до линии действия силы
Плечо силы относительно точки B равно 3м.
Примеры решения задач >
Момент силы >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Формула плеча силы в физике
Формула плеча силы
Определение и формула плеча силы
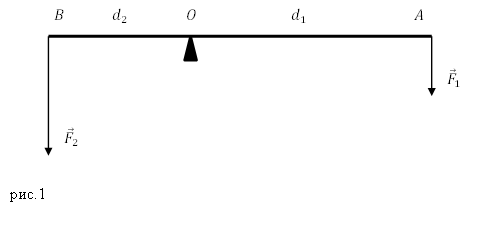
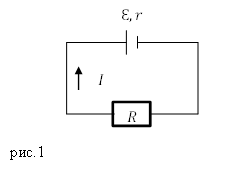
Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${overline{F}}_1$ и ${overline{F}}_2$, действующие на рычаг направлены в одну сторону.
Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.
Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $left|OAright|=d_1$- плечо силы $F_1$; $left|OAright|=d_2$- плечо силы $F_2$.
Рычаг находится в состоянии равновесия, если выполняется равенство:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1right).]
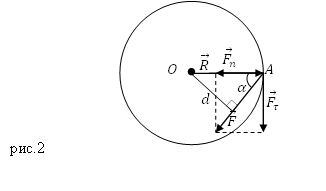
Предположим, что материальная точка движется по окружности (рис.2) под действием силы $overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($varepsilon $) точки определяется тангенциальной составляющей ($F_{tau }$) силы $overline{F}$:
[mRvarepsilon =F_{tau }left(2right),]
где $m$ – масса материальной точки; $R$ – радиус траектории движения точки; $F_{tau }$ – проекция силы на направление скорости движения точки.
Если угол $alpha $ – это угол между вектором силы $overline{F}$ и радиус – вектором $overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:
[F_{tau }=F{sin alpha left(3right). }]
Расстояние $d$ между центром O и линией действия силы $overline{F}$ называют плечом силы. Из рис.2 следует, что:
[d=R{sin alpha left(4right). }]
Если на точку будет действовать сила ($overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $alpha $ станет равен $frac{pi }{2}$.
Момент силы и плечо
Понятие плечо силы иногда используют, для записи величины момента силы ($overline{M}$), который равен:
[overline{M}=left[overline{r}overline{F}right]left(5right),]
где $overline{r}$ – радиус – вектор проведенный к точке продолжения силы$ overline{F}$. Модуль вектора момента силы равен:
[M=F{rsin alpha = }Fd left(6right).]
Построение плеча силы
И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз). При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.
Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).
Примеры задач с решением
Пример 1
Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={rm 2 }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?
Решение. Основой решения задачи является правило равновесия рычага:
[frac{F_1}{F_2}=frac{d_2}{d_1}left(1.1right),]
где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:
[frac{m_1g}{m_2g}=frac{d_2}{d_1}to frac{m_1}{m_2}=frac{d_2}{d_1}left(1.2right).]
Из выражения (1.2) получим искомую массу $m_1$:
[m_1=frac{m_2d_2}{d_1}.]
Вычислим искомую массу:
[m_1=2cdot frac{1}{4}=0,5 (кг).]
Ответ. $m_1=0,5 кг$
Пример 2
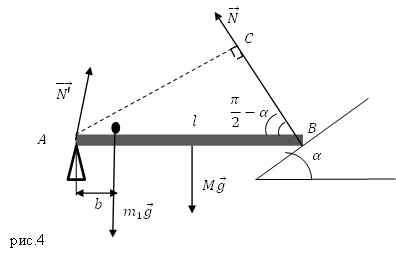
Задание. Однородный стержень длинной $l $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $alpha $. На стержне на расстоянии $b $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?
Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $Moverline{g}$, вес груза, расположенного на нем $overline{P}=m_1overline{g}$, сила реакции наклонной плоскости: $overline{N}$; сила реакции опоры в точке A: $overline{N}’$.
Плечи сил будем искать относительно точки A. Плечо силы $overline{N’}$ будет равно нулю, так как сила приложена к стержню в точке А:
[d_{N’}=0 left(2.1right).]
Плечо другой силы реакции опоры ($overline{N}$) равно длине перпендикуляра AC:
[d_N=l{sin (90-alpha ) }=l{cos alpha left(2.2right). }]
Плечо силы $Moverline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:
[d_{Mg}=frac{l}{2}left(2.3right).]
Плечо силы $m_1overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:
[d_{m_1g}=b.]
Ответ. $d_{N’}=0;; d_N=l{sin (90-alpha ) }=l{cos alpha left(мright), }d_{Mg}=frac{l}{2}, d_{m_1g}=b$
Читать дальше: формула полезной мощности.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Момент силы. Условия равновесия рычага
- Устройство и виды рычагов
- Момент силы
- Правило моментов для двух сил
- Правило моментов для нескольких сил
- Применение рычагов в быту и технике
- Задачи
- Лабораторная работа №9. Проверка условия равновесия рычага
п.1. Устройство и виды рычагов
 |
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
Рычаг состоит из перекладины и опоры. Назначение рычага – получить выигрыш в силе или расстоянии. |
В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.
п.2. Момент силы
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
На рисунке (l_1) – плечо силы (F_1, l_2) – плечо силы (F_2).
Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.
Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.
На рисунке сила (F_1) вращает рычаг против часовой стрелки, а сила (F_2) – по часовой стрелке.
Момент силы – это произведение силы, вращающей тело, на её плечо. $$ M=Fl $$ В системе СИ единица измерения момента силы – Н·м.
Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.
п.3. Правило моментов для двух сил
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
$$ F_1l_1=F_2l_2 $$ |
п.4. Правило моментов для нескольких сил
Правило моментов для нескольких сил
Рычаг находится в равновесии, если сумма моментов всех сил, вращающих его по ходу часовой стрелки, равен сумме моментов всех сил, вращающих его против хода часовой стрелки.
Например:
 |
Силы (F_1, F_2, F_3) вращают рычаг против часовой стрелки, а сила (F_4) – по часовой стрелке. Поэтому: $$ F_1l_1+F_2l_2+F_3l_3=F_4l_4 $$ |
п.5. Применение рычагов в быту и технике
Рычаги первого рода
 Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры. |
 Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект. |
 Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя. |
 Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз. |
 Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры. Нагрузка — сопротивление предмета захвату инструментом. |
 Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям. |
Рычаги второго рода
Рычаги третьего рода
п.6. Задачи
Задача 1. Для каждого положения тела укажите плечо силы.
При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.
Задача 2. Грузы уравновешены на рычаге. Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.
Дано:
(frac{l_1}{l_2}=frac 15)
(m_1=2,5 text{кг})
__________________
(m_2-?)
По правилу моментов begin{gather*} F_1l_1=F_2l_2 end{gather*} На обоих концах рычага действуют силы тяжести: $$ F_1=m_1g, F_2=m_2g $$ Получаем: begin{gather*} m_1gl_1=m_2gl_2\[7pt] m_2=frac{m_1l_1}{l_2} end{gather*} Подставляем: $$ m_2=2,5cdot frac 15=0,5 (text{кг}) $$ Ответ: 0,5 кг
Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?
Дано:
(F_1=15 text{Н})
(F_2=60 text{Н})
(l_1+l_2=1 text{м})
__________________
(l_1, l_2-?)
По правилу моментов begin{gather*} F_1l_1=F_2l_2. end{gather*} Получаем систему уравнений begin{gather*} left{ begin{array}{l l} 15l_1=60l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 4l_2+l_2=1 end{array} right. Rightarrow \[7pt] Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 5l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=0,8 \ l_2=0,2 end{array} right. end{gather*} Ответ: 0,8 м от точки приложения первой силы и 0,2 м от точки приложения второй силы.
Задача 4*. К балке, расположенной на двух опорах А и В подвешен груз массой 500 кг. Расстояние от точки подвеса груза к одному из концов балки в 4 раза больше, чем к другому. С какой силой балка давит на каждую из опор? Примите (gapprox 10 text{м/с}^2). Ответ запишите в килоньютонах.
Дано:
(m=500 text{кг})
(gapprox 10 text{м/с}^2)
(OB=4OA)
__________________
(F_A, F_B-?)
Сила тяжести (F_{text{т}}=mg), направленная вниз, уравновешивается силами реакции опор (F_A) и (F_B), направленными вверх. begin{gather*} F_A+F_B=mg end{gather*} По правилу моментов при равновесии begin{gather*} F_Acdot OA=F_Bcdot OB=F_Bcdot 4OARightarrow F_A=4F_B \[7pt] F_A+F_B=5F_B=mgRightarrow F_B=frac{mg}{5} end{gather*} Получаем: begin{gather*} F_B=frac{500cdot 10}{5}=1000 text{Н}=1 text{кН}, F_A=4cdot 100=4000 text{Н}=4 text{кН} end{gather*} Ответ: 4 кН и 1 кН
п.7. Лабораторная работа №9. Проверка условия равновесия рычага
Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.
Теоретические сведения
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг. Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
Момент силы – это произведение силы, вращающей тело, на её плечо: (M=Fl).
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
begin{gather*} M_1=M_2\[7pt] F_1l_1=F_2l_2 end{gather*} |
В работе используется лабораторный рычаг с отверстиями диаметром 4 мм, находящимися на расстоянии 5 см друг от друга. Отверстий нечетное количество; центральное отверстие (центр тяжести) используется для подвеса рычага на штативе в положении равновесия. Абсолютную погрешность определения плеча на данном рычаге принимаем равной половине диаметра отверстия $$ Delta l=frac D2=2 text{мм} $$
Для измерения веса груза используется динамометр с ценой деления $$ d=0,1 text{Н}. $$
Абсолютная погрешность определения веса $$ Delta_F=frac d2=0,05 text{Н}. $$
Относительные погрешности измерений: $$ delta_l=frac{Delta_l}{l}, delta_F=frac{Delta_F}{F}, delta_M=delta_l+delta_F $$
Абсолютная погрешность определения момента силы $$ Delta_M=Mcdot delta_M $$
Погрешности определения отношений сил и плечей: begin{gather*} r_F=frac{F_1}{F_2}, delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}, Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}\[7pt] r_l=frac{l_2}{l_1}, delta_{rF}=delta_{rl}frac{Delta_l}{l_1}+frac{Delta_l}{l_2}, Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl} end{gather*}
Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.
Ход работы
1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
2. Подвесьте три груза на динамометре, запишите их вес (F_1).
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил (M_1) и (M_2), их относительные и абсолютные погрешности.
7. Вычислите отношение сил (frac{F_1}{F_2}) и плеч (frac{l_2}{l_1}) для этого случая, погрешности их определения.
8. Сделайте выводы.
Результаты измерений и вычислений
| (F_1, text{Н}) | (l_1, text{см}) | (F_2, text{Н}) | (l_2, text{см}) | (F_1/F_2) | (l_2/l_1) |
| 2,9 | 5 | 1,0 | 15 | 2,9 | 3,0 |
Погрешности прямых измерений: $$ Delta_l=2 text{мм}=0,2 text{см}, Delta_F=0,05 text{Н} $$ Найдем моменты сил и погрешности вычислений: begin{gather*} M_1=F_1cdot l_1=2,9cdot 5=14,5 (text{Н}cdot text{м})\[7pt] delta_{M1}=frac{Delta_l}{l_1}+frac{Delta_F}{F_1}=frac{0,2}{5}+frac{0,05}{2,9}approx 0,04+0,017=0,057=5,7text{%} \[7pt] Delta_{M1}=M_1cdot delta_{M1}=14,5cdot 0,057approx 0,8 (text{Н}cdot text{м})\[7pt] M_1=(14,5pm 0,8) text{Н}cdot text{м}\[7pt] \[7pt] M_2=F_2cdot l_2=1,0cdot 15=15,0 (text{Н}cdot text{м})\[7pt] delta_{M2}=frac{Delta_l}{l_2}+frac{Delta_F}{F_2}=frac{0,2}{15}+frac{0,05}{1,0}approx 0,013+0,05=0,063=6,3 text{%} \[7pt] Delta_{M2}=M_2cdot delta_{M2}=15,0cdot 0,063approx 0,9 (text{Н}cdot text{м})\[7pt] M_2=(15,0pm 0,9) text{Н}cdot text{м} end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ M_1=M_2 $$
Погрешность вычислений для (frac{F_1}{F_2}) begin{gather*} delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}=frac{0,05}{2,9}+frac{0,05}{1,0}approx 0,017+0,05=0,067=6,7text{%}\[7pt] Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}=2,9cdot 0,067approx 0,2\[7pt] frac{F_1}{F_2}=2,9pm 0,2 end{gather*}
Погрешность вычислений для (frac{l_2}{l_1}) begin{gather*} delta_{rl}=frac{Delta_l}{l_1}+frac{Delta_l}{l_2}=frac{0,2}{5}+frac{0,2}{15}approx 0,04+0,013=0,053=5,3text{%}\[7pt] Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl}=3,0cdot 0,053approx 0,2\[7pt] frac{l_2}{l_1}=3,0pm 0,2 end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ frac{F_2}{F_2}=frac{l_2}{l_1} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Моменты сил, приложенных слева и справа от оси вращения рычага, равны $$ M_1=(14,5pm 0,8) text{Н}cdot text{м}, M_2=(15,0pm 0,9) text{Н}cdot text{м} $$ Таким образом, с учетом вычисленных погрешностей, (M_1=M_2) – правило моментов выполняется.
Отношения сил и плечей равны begin{gather*} frac{F_1}{F_2}=2,9pm 0,2, frac{l_2}{l_1}=3,0pm 0,2 end{gather*}
Таким образом, с учетом вычисленных погрешностей (frac{F_1}{F_2}=frac{l_2}{l_1}) – правило отношений выполняется.
Эксперименты подтвердили условие равновесия рычага.
- Подробности
- Обновлено 20.01.2019 00:33
- Просмотров: 566
1. Что такое рычаг?
Самый простой и распространенный механизм — рычаг.
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.
2. Как используют рычаг?
Можно для поднятия груза использовать в качестве рычага лом.
Для этого надо с силой F нажимать на конец лома В или приподнимать конец В.
В любом случае при поднятии груза необходимо преодолеть вес груза Р — силу, направленную вертикально вниз.
Для этого надо повернуть лом вокруг оси, проходящей через неподвижную точку лома — точку его опоры О.
Сила F, с которой человек действует на рычаг, меньше силы Р.
Используя рычаг, получаем выигрыш в силе.
2. Что называют плечом силы?
Например, есть рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В.
F1 и F2, действующие на рычаг, направлены в одну сторону.
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
3. Как найти плечо силы? Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Длина этого перпендикуляра и будет плечом данной силы.
OA — плечо силы F1,
OB — плечо силы F2.
4. Какое действие оказывают на рычаг силы?
Силы, действующие на рычаг, могут повернуть его вокруг оси или по ходу, или против хода часовой стрелки.
На рисунке выше:
С
ила F2 вращает рычаг по ходу часовой стрелки.
Сила F1 вращает рычаг против хода часовой стрелки.
Результат действия силы зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу и как направлена.
5. В чем состоит правило (условие) равновесия рычага?
Правило равновесия рычага было установлено Архимедом (287—212 гг. до н. э.).
Правило (условие) равновесия рычага:
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.

Например:
К рычагу по обе стороны от точки опоры подвешивают грузы так, чтобы рычаг оставался в равновесии.
Действующие на рычаг силы равны весам этих грузов.
Далее измеряют модули сил и их плечи.
Если сила F2 уравновешивает силу F1, то плечо меньшей силы в 2 раза больше плеча большей силы.

где
F1 и F2 — силы, действующие на рычаг,
l1 и l2 — плечи этих сил.
6. Как уравновесить меньшей силой большую?
При помощи рычага можно меньшей силой уравновесить большую силу.
При этом плечо меньшей силы должно быть длиннее плеча большей силы.
Например:
Задача.
Человеку необходимо поднять с помощью рычага плиту массой 240 кг.
Большее плечо рычага равно 2,4 м.
Меньшее плечо рычага равно 0,6 м.
Какую силу надо приложить человеку к большему плечу рычага?
Человек преодолевает силу 2400 Н, прикладывая свою силу, равную 600 Н.
Здесь рычаг дает выигрыш в силе в 4 раза.
Однако плечо, на которое действует человек, в 4 раза длиннее того, на которое действует вес плиты:
2,4 м : 0,6 м = 4.
Следующая страница – смотреть
Назад в “Оглавление” – смотреть