Что такое работа выхода как ее найти

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 декабря 2021 года; проверки требуют 15 правок.

Рабо́та вы́хода — разность значений энергий уровня вакуума и уровня Ферми , то есть минимальная энергия, которую необходимо сообщить электрону для его «непосредственного» удаления из объёма твёрдого тела, обычно металла или полупроводника:

Работа выхода обычно указывается в электрон-вольтах, типичные величины лежат в диапазоне 3—5 эВ.

Возможные обозначения: и другие.

Здесь «непосредственность» означает то, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности по атомным масштабам, достаточным чтобы электрон прошёл весь двойной слой, но достаточно близко по сравнению с размерами макроскопических граней кристалла.

Определение и комментарий[править | править код]

Работа выхода находится как где энергия уровня вакуума берётся на небольшом расстоянии от места выхода электрона из образца, хотя и значительно большем, чем постоянная кристаллической решётки.

При удалении электрона от поверхности его взаимодействие с зарядами, остающимися внутри твёрдого тела, приводит к индуцированию поверхностных зарядов (в электростатике для расчёта взаимодействия применяется «метод изображения заряда»). Удаление электрона на бесконечность происходит в поле индуцированного поверхностного заряда на что требуется дополнительная работа, зависящая от диэлектрической проницаемости вещества, геометрии образца и свойств всех его поверхностей.

При нахождении величины удаление от конкретной грани полагается небольшим, и эта дополнительная работа не учитывается. оказывается разной для различных кристаллографических плоскостей поверхности вещества. В отличие от работа по перемещению электрона далее в бесконечность не зависит от того, через какую плоскость был удален электрон, ввиду потенциальности электростатического поля.

Работа выхода в фотоэффекте[править | править код]

Работа выхода во внешнем фотоэффекте — минимальная энергия фотонов, необходимая для удаления электрона из вещества под действием света при

Работа выхода из различных металлов[править | править код]

Единицей измерения работы в СИ являются джоуль (Дж), но в физике твердого тела принято использовать электронвольт (эВ)^[1].
Диапазоны изменения работы выхода для типичных кристаллографических плоскостей указаны в таблице^[2]:

Элемент	эВ	Элемент	эВ	Элемент	эВ	Элемент	эВ	Элемент	эВ
Ag:	4,52 — 4,74	Al:	4,06 — 4,26	As:	3,75	Au:	5,1 — 5,47	B:	~4,45
Ba:	2,52 — 2,7	Be:	4,98	Bi:	4,31	C:	~5	Ca:	2,87
Cd:	4,08	Ce:	2,9	Co:	5	Cr:	4,5	Cs:	2,14
Cu:	4,53 — 5,10	Eu:	2,5	Fe:	4,67 — 4,81	Ga:	4,32	Gd:	2,90
Hf:	3,9	Hg:	4,475	In:	4,09	Ir:	5,00 — 5,67	K:	2,29
La:	3,5	Li:	2,93	Lu:	~3,3	Mg:	3,66	Mn:	4,1
Mo:	4,36 — 4,95	Na:	2,36	Nb:	3,95 — 4,87	Nd:	3,2	Ni:	5,04 — 5,35
Os:	5,93	Pb:	4,25	Pd:	5,22 — 5,6	Pt:	5,12 — 5,93	Rb:	2,261
Re:	4,72	Rh:	4,98	Ru:	4,71	Sb:	4,55 — 4,7	Sc:	3,5
Se:	5,9	Si:	4,60 — 4,85	Sm:	2,7	Sn:	4,42	Sr:	~2,59
Ta:	4,00 — 4,80	Tb:	3,00	Te:	4,95	Th:	3,4	Ti:	4,33
Tl:	~3,84	U:	3,63 — 3,90	V:	4,3	W:	4,32 — 5,22	Y:	3,1
Yb:	2,60[3]	Zn:	3,63 — 4,9	Zr:	4,05

Работу выхода можно определить методом контактной разности потенциалов, основанном на сравнении работ выхода из металлов – эталонного и контролируемого^[4].

Работа выхода для полупроводника[править | править код]

Для полупроводников работа выхода определяется точно так же, как и для металлов (и данные для некоторых собственных полупроводников включены в таблицу).

На практике полупроводник обычно легирован и величина зависит от типа и концентрации легирующих примесей. Уровень при сильном легировании донорами находится у края зоны проводимости , а при сильном легировании акцепторами — близко к краю валентной зоны (соответственно, вариации составляют около ширины запрещённой зоны

Более универсальной величиной, вместо для полупроводников является энергия сродства к электрону, равная Например, для кремния сродство составляет 4,05 эВ, а работа выхода примерно от 4,0 до 5,2 эВ (для собственного материала около 4,6 эВ).

Примечания[править | править код]

Литература[править | править код]

• Solid State Physics, by Ashcroft and Mermin. Thomson Learning, Inc, 1976
• Гончаренко В.И., Олешко В.С. Метод контактной разности потенциалов в оценке энергетического состояния поверхности металлических деталей авиационной техники: монография. – М.: Изд-во МАИ, 2019. – 160 с. – ISBN 978-5-4316-0631-1 http://elibrary.mai.ru/MegaPro/UserEntry?Action=Link_FindDoc&id=68387&idb=0

        энергия, затрачиваемая на удаление электрона из твёрдого тела или жидкости в вакуум. Переход электрона из вакуума в конденсированную среду сопровождается выделением энергии, равной Р. в. Следовательно, Р. в. является мерой связи электрона с конденсированной средой; чем меньше Р. в., тем легче происходит эмиссия электронов. Поэтому, например, плотность тока термоэлектронной эмиссии (См. Термоэлектронная эмиссия) или автоэлектронной эмиссии (см. Туннельная эмиссия) экспоненциально зависит от Р. в.

         Р. в. наиболее полно изучена для проводников, особенно для металлов (См. Металлы). Она зависит от кристаллографической структуры поверхности. Чем плотнее «упакована» грань кристалла, тем выше Р. в. φ. Например, для чистого вольфрама φ = 4,3 эв для граней {116} и 5,35 эв для граней {110}. Для металлов возрастание (усреднённых по граням) φ приблизительно соответствует возрастанию потенциала ионизации. Наименьшие Р. в. (2 эв) свойственны щелочным металлам (Cs, Rb, К), а наибольшие (5,5 эв) — металлам группы Pt.

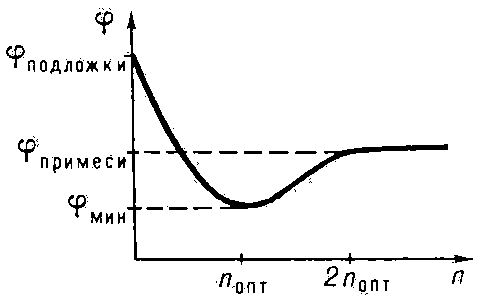
         Р. в. чувствительна к дефектам структуры поверхности. Наличие на плотноупакованной грани собственных неупорядоченно расположенных атомов уменьшает φ. Ещё более резко φ зависит от поверхностных примесей: электроотрицательные примеси (кислород, галогены, металлы с φ, большей, чем φ подложки) обычно повышают φ, а электроположительные — понижают. Для большинства электроположительных примесей (Cs на W, Tn на W, Ba на W) наблюдается снижение Р. в., которая достигает при некоторой оптимальной концентрации примесей n_oпт минимального значения, более низкого, чем φ основного металла; при n ≈ 2n_oпт Р. в. становится близкой к φ металла покрытия и далее не изменяется (см. рис.). Величине n_oпт соответствует упорядоченный, согласованный со структурой подложки слой атомов примеси, как правило, с заполнением всех вакантных мест; а величине 2n_oпт — плотный моноатомный слой (согласование со структурой подложки нарушено). Т. о., Р. в. по крайней мере для материалов с металлической электропроводностью определяется свойствами их поверхности.

         Электронная теория металлов рассматривает Р. в. как работу, необходимую для удаления электрона с Ферми уровня в вакуум. Современная теория не позволяет пока точно вычислить φ для заданных структур и поверхностей. Основные сведения о значениях φ даёт эксперимент. Для определения φ используют эмиссионные или контактные явления (см. Контактная разность потенциалов).

Знание Р. в. существенно при конструировании электровакуумных приборов (См. Электровакуумные приборы), где используется эмиссия электронов или ионов, а также в таких, например, устройствах, как термоэлектронные преобразователи (См. Термоэлектронный преобразователь) энергии.

Лит.: Добрецов Л. Н., Гомоюнова М. В., Эмиссионная электроника, М., 1966; Зандберг Э. Я., Ионов Н. И., Поверхностная ионизация, М., 1969.

В. Н. Шредник.

        Зависимость работы выхода φ от поверхностной концентрации n электроположительных примесных атомов.

Физика, 11 класс

Урок 22. Фотоэффект

Перечень вопросов, рассматриваемых на уроке:

• предмет и задачи квантовой физики;
• гипотеза М. Планка о квантах;
• опыты А.Г. Столетова;
• определение фотоэффекта, кванта, тока насыщения, задерживающего напряжения, работы выхода, красной границы фотоэффекта;
• уравнение Эйнштейна для фотоэффекта;
• законы фотоэффекта.

Глоссарий по теме:

Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Фотоэффект – это вырывание электронов из вещества под действием света.

Квант – (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике.

Ток насыщения – некоторое предельное значение силы фототока.

Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.

Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.

Основная и дополнительная литература по теме урока:

1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.

2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.

3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г. С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.

4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.

Теоретический материал для самостоятельного изучения

В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.

Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.

Коэффициент пропорциональности получил название постоянной Планка, и она равна:

h = 6,63 ∙ 10^-34 Дж∙с.

После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.

Квантовая физика – раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.

Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.

В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.

Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.

Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.

Схема установки для изучения законов фотоэффекта

Первый закон фотоэффекта: фототок насыщения – максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, – прямо пропорционален интенсивности падающего излучения.

Зависимость силы тока от приложенного напряжения

Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.

Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.

Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.

hν_min = A_в

где А_в – работа выхода электронов;

h – постоянная Планка;

ν_min – частота излучения, соответствующая красной границе фотоэффекта;

с – скорость света;

λкр – длина волны, соответствующая красной границе_.

Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.

Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.

Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.

Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, “затрудняющее” вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.

Задерживающее напряжение – минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.

Задерживающее напряжение

Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:

где – максимальная кинетическая энергия электронов;

Е – заряд электрона;

– задерживающее напряжение.

Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:

В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».

Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны – фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.

Примеры и разбор решения заданий

1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?

Для каждой величины определите соответствующий характер изменения:

1) увеличится

2) уменьшится

3) не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Работа выхода	Запирающее напряжение

Решение:

Работа выхода – это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.

Запирающее напряжение – это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:

Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.

Ответ:

Работа выхода	Запирающее напряжение
не изменится	увеличится

2. Красная граница фотоэффекта для вещества фотокатода λ₀ = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.

Решение.

Запишем уравнение для фотоэффекта через длину волны:

Условие связи красной границы фотоэффекта и работы выхода:

Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:

Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:

Подставляя численные значения, получаем: λ ≈ 215 нм.

Ответ: λ ≈ 215 нм.

Работа выхода

Рабо́та вы́хода, работа, которую необходимо затратить для удаления электрона из конденсированной фазы вещества в вакуум. Измеряется разностью между минимальной энергией электрона в вакууме и ферми-энергией электрона внутри вещества.

При оценке работы выхода предполагается, что электрон удаляется из твёрдого тела через данную поверхность и перемещается в точку, которая расположена достаточно далеко от поверхности тела (по атомным масштабам), но достаточно близко по сравнению с размерами макроскопических граней тела. Переход электрона из вакуума в конденсированную среду сопровождается выделением энергии, равной работе выхода. Следовательно, работа выхода является мерой связи электрона с конденсированной средой.

Обычно величина работы выхода используется для характеристики явлений термоэлектронной эмиссии. Чем меньше работа выхода, тем легче происходит эмиссия электронов. Для металлов увеличение работы выхода приблизительно соответствует росту ионизационного потенциала. Наименьшие для металлов работы выхода (2 эВ) свойственны щелочным металлам (Cs, Rb, K), наибольшие (5,5 эВ) – металлам платиновой группы.

В кристаллических структурах работа выхода существенно зависит от кристаллографической структуры поверхности. Она тем больше, чем плотнее «упакована» грань кристалла; например, для чистого вольфрама работа выхода равна 4,3 эВ для граней {116} и 5,35 эВ для граней {110}.

Работа выхода чувствительна к дефектам структуры поверхности (наличие на плотноупакованной грани собственных неупорядоченно расположенных атомов уменьшает её) и к поверхностным примесям (электроотрицательные примеси обычно повышают работу выхода, электроположительные – понижают).

Знание величин работы выхода существенно при конструировании различных электровакуумных приборов. Эти величины определяют экспериментально, используя эмиссионные или контактные явления.

Единица измерения работы выхода – джоуль [Дж, единица СИ (SI)] или электронвольт (эВ, внесистемная единица); 1 эВ=1,6⋅10–19 Дж1,text{эВ} = 1,6 cdot 10^{–19},text{Дж}.

Дата публикации:  16 января 2023 г. в 23:39 (GMT+3)

5

Лекция 7

Электрический
ток в различных средах

Вопросы

1. Работа выхода
электронов из металла. Контактная
разность потенциалов. Законы Вольты.

2. Термоэлектрические
явления и их применение.

1. Работа выхода
   электронов из металла.

Контактная
разность потенциалов. Законы Вольты

Работой
выхода
называется
работа, которую нужно затратить для
удаления электрона из металла в вакуум.

Причины появления работы
выхода

1. Электрон, вылетая,
   притягивается к индуцированному им
   положительному электрическому заряду.

2. Электронное
   облако
   образует двойной
   электрический слой,
   поле которого подобно полю плоского
   конденсатора.

Поле двойного
электрического слоя характеризуется
разностью потенциалов ,
поэтому работа выхода электрона

А
= e
(1)

Работу выхода
измеряют в электрон-вольтах
(эВ).

1
электрон-вольт
(эВ) равен работе перемещения электрона
в электрическом поле между точками с
разностью потенциалов 1 В.

Связь размерностей
работы эВ
и Дж

1 эВ = 1,610^-19
Кл 
1 В = 1,610^-19
Дж

(2)

Работа выхода
электронов

Вещество	А, эВ	Вещество	А, эВ
Алюминий Вода Натрий Калий Медь Вольфрам	4,20 6,10 2,28 2,00 4,36 4,50	Окись бария Окись цезия Цезий Цинк Серебро Платина	1,0 – 1,6 1,0 -1,2 1,94 4,25 4,74 5,30

Законы Вольты

1. Контактная
   разность потенциалов
   двух разнородных металлов зависит
   только от их химического состава и
   температуры.

2. Контактная
   разность потенциалов
   последовательно соединенных различных
   проводников, находящихся при одинаковой
   температуре, не зависит от химического
   состава промежуточных проводников и
   равна контактной разности потенциалов,
   возникающей при непосредственном
   соединении крайних проводников.

Появление контактной
разности потенциалов обусловлено двумя
причинами:

1. 

   Различием в работе выхода
   электронов;

При А₁
< A₂
поле

остановит перекачку электронов, в
результате появляется внешняя
контактная разность потенциалов:

. (3)

1. Различием
   концентрации электронного газа;
   электроны ведут себя подобно молекулам
   воздуха в поле тяготения Земли. При
   

(4)

(А
= А₂

А₁
= mgh
в барометрической формуле). Из (3, 4)
следует, что

,

– внутренняя
контактная разность потенциалов
(5)

Это математическое
выражение первого закона Вольты.

Внутренняя
контактная разность потенциалов
возникает в двойном электрическом слое,
образующемся в приконтактной области,
называемом контактным
слоем.
Толщина контактного слоя в металлах
10^-10
м, число электронов, участвующих в
диффузии через контактный слой, мало
(около 2% от электронов на поверхности
металла), поэтому ток проходит через
контакт легко и не связан с односторонней
проводимостью.

2. Термоэлектрические
явления и их применение

Возникновение ЭДС на
границе контакта двух разнородных
проводников

,
(6)

где


постоянная термоЭДС для спая металлов.

Таблица
1

Значения постоянной
термоЭДС относительно платины при 0^оС

№ пп	Металл	, мкВ/K
1	Медь	7,4
2	Никель	16,4
3	Висмут	65,0
4	Теллуристый свинец	300
5	Закись меди	1000

Явление Зеебека

В
замкнутой цепи, состоящей из последовательно
соединенных разнородных проводников,
контакты между которыми имеют различную
температуру, возникает электрический
ток.

Применение:

• Термопары (датчики
  температуры), точность до 0,01 К;

• Термобатареи для
  генерации электрического тока (КПД до
  18%).

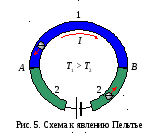
Явление Пельтье

При
прохождении через контакт двух различных
проводников электрического тока в
зависимости от его направления помимо
джоулевой теплоты выделяется или
поглощается дополнительная
теплота.

На рис. 5 спай А
будет охлаждаться В

нагреваться.

Применение:

• Термоэлектрические
  полупро­вод­ни­ко­вые холодильники;

Явление Томсона
(Вильям
Томсон, Кельвин)

При
прохождении тока по неравномерно
нагретому проводнику происходит
дополнительное выделение (поглощение)
теплоты.

В более нагретой
части проводника электроны имеют большую
среднюю энергию, чем в менее нагретой
части. Двигаясь в направлении убывания
температуры, они отдают часть своей
энергии решетке, в результате чего
выделяется теплота Томсона.

Например, при
сварке металлов постоянным током
смещается тепловой центр по сравнению
со сваркой переменным током.