Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
Матрица $A^{-1}$ называется обратной по отношению к квадратной матрице $A$, если выполнено условие $A^{-1}cdot A=Acdot A^{-1}=E$, где $E$ – единичная матрица, порядок которой равен порядку матрицы $A$.
Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.
Обратная матрица $A^{-1}$ существует тогда и только тогда, когда матрица $A$ – невырожденная. Если обратная матрица $A^{-1}$ существует, то она единственная.
Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.
Метод присоединённой (союзной) матрицы
Пусть задана матрица $A_{ntimes n}$. Для того, чтобы найти обратную матрицу $A^{-1}$, требуется осуществить три шага:
- Найти определитель матрицы $A$ и убедиться, что $Delta Aneq 0$, т.е. что матрица А – невырожденная.
- Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{ntimes n}^{*}=left(A_{ij} right)$ из найденных алгебраических дополнений.
- Записать обратную матрицу с учетом формулы $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$.
Матрицу ${A^{*}}^T$ часто именуют присоединённой (взаимной, союзной) к матрице $A$.
Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.
Пример №1
Найти матрицу, обратную к матрице $A=left( begin{array} {cccc} 5 & -4 &1 & 0 \ 12 &-11 &4 & 0 \ -5 & 58 &4 & 0 \ 3 & -1 & -9 & 0 end{array} right)$.
Решение
Так как все элементы четвёртого столбца равны нулю, то $Delta A=0$ (т.е. матрица $A$ является вырожденной). Так как $Delta A=0$, то обратной матрицы к матрице $A$ не существует.
Ответ: матрицы $A^{-1}$ не существует.
Пример №2
Найти матрицу, обратную к матрице $A=left(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)$. Выполнить проверку.
Решение
Используем метод присоединённой матрицы. Сначала найдем определитель заданной матрицы $A$:
$$
Delta A=left| begin{array} {cc} -5 & 7\ 9 & 8 end{array}right|=-5cdot 8-7cdot 9=-103.
$$
Так как $Delta A neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
begin{aligned}
& A_{11}=(-1)^2cdot 8=8; ; A_{12}=(-1)^3cdot 9=-9;\
& A_{21}=(-1)^3cdot 7=-7; ; A_{22}=(-1)^4cdot (-5)=-5.\
end{aligned}
Составляем матрицу из алгебраических дополнений: $A^{*}=left( begin{array} {cc} 8 & -9\ -7 & -5 end{array}right)$.
Транспонируем полученную матрицу: ${A^{*}}^T=left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$ (полученная матрица часто именуется присоединённой или союзной матрицей к матрице $A$).
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, имеем:
$$
A^{-1}=frac{1}{-103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)
=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)
$$
Итак, обратная матрица найдена:
$$A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right).$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $A^{-1}cdot A=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$, а в виде $-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$:
$$
A^{-1}cdot{A}
=-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)cdotleft(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)
=-frac{1}{103}cdotleft(begin{array} {cc} -103 & 0 \ 0 & -103 end{array}right)
=left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array}right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$.
Пример №3
Найти обратную матрицу для матрицы $A=left( begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right)$. Выполнить проверку.
Решение
Начнём с вычисления определителя матрицы $A$. Итак, определитель матрицы $A$ таков:
$$
Delta A=left| begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right| = 18-36+56-12=26.
$$
Так как $Delta Aneq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
$$
begin{aligned}
& A_{11}=(-1)^{2}cdotleft|begin{array}{cc} 9 & 4\ 3 & 2end{array}right|=6;;
A_{12}=(-1)^{3}cdotleft|begin{array}{cc} -4 &4 \ 0 & 2end{array}right|=8;;
A_{13}=(-1)^{4}cdotleft|begin{array}{cc} -4 & 9\ 0 & 3end{array}right|=-12;\
& A_{21}=(-1)^{3}cdotleft|begin{array}{cc} 7 & 3\ 3 & 2end{array}right|=-5;;
A_{22}=(-1)^{4}cdotleft|begin{array}{cc} 1 & 3\ 0 & 2end{array}right|=2;;
A_{23}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 7\ 0 & 3end{array}right|=-3;\
& A_{31}=(-1)^{4}cdotleft|begin{array}{cc} 7 & 3\ 9 & 4end{array}right|=1;;
A_{32}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 3\ -4 & 4end{array}right|=-16;;
A_{33}=(-1)^{6}cdotleft|begin{array}{cc} 1 & 7\ -4 & 9end{array}right|=37.
end{aligned}
$$
Составляем матрицу из алгебраических дополнений и транспонируем её:
$$
A^*=left( begin{array} {ccc} 6 & 8 & -12 \ -5 & 2 & -3 \ 1 & -16 & 37end{array} right); ;
{A^*}^T=left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, получим:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)=
left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)
$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $Acdot A^{-1}=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$, а в виде $frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)$:
$$
Acdot{A^{-1}}
=left( begin{array}{ccc}
1 & 7 & 3 \
-4 & 9 & 4\
0 & 3 & 2end{array} right)cdot
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)
=frac{1}{26}cdotleft( begin{array} {ccc} 26 & 0 & 0 \ 0 & 26 & 0 \ 0 & 0 & 26end{array} right)
=left( begin{array} {ccc} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1end{array} right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$.
Пример №4
Найти матрицу, обратную матрице $A=left( begin{array} {cccc} 6 & -5 & 8 & 4\ 9 & 7 & 5 & 2 \ 7 & 5 & 3 & 7\ -4 & 8 & -8 & -3 end{array} right)$.
Решение
Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.
Например, для первой строки получим:
$$
A_{11}=left|begin{array}{ccc} 7 & 5 & 2\ 5 & 3 & 7\ 8 & -8 & -3 end{array}right|=556;;
A_{12}=-left|begin{array}{ccc} 9 & 5 & 2\ 7 & 3 & 7 \ -4 & -8 & -3 end{array}right|=-300;
$$
$$
A_{13}=left|begin{array}{ccc} 9 & 7 & 2\ 7 & 5 & 7\ -4 & 8 & -3 end{array}right|=-536;;
A_{14}=-left|begin{array}{ccc} 9 & 7 & 5\ 7 & 5 & 3\ -4 & 8 & -8 end{array}right|=-112.
$$
Определитель матрицы $A$ вычислим по следующей формуле:
$$
Delta{A}=a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}+a_{14}cdot A_{14}=6cdot 556+(-5)cdot(-300)+8cdot(-536)+4cdot(-112)=100.
$$
А далее продолжаем находить алгебраические дополнения:
$$
begin{aligned}
& A_{21}=-77;;A_{22}=50;;A_{23}=87;;A_{24}=4;\
& A_{31}=-93;;A_{32}=50;;A_{33}=83;;A_{34}=36;\
& A_{41}=473;;A_{42}=-250;;A_{43}=-463;;A_{44}=-96.
end{aligned}
$$
Матрица из алгебраических дополнений:
$$A^*=left(begin{array}{cccc} 556 & -300 & -536 & -112\ -77 & 50 & 87 & 4 \ -93 & 50 & 83 & 36\ 473 & -250 & -463 & -96end{array}right)$$
Присоединённая матрица:
$${A^*}^T=left(begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96end{array}right)$$
Обратная матрица:
$$
A^{-1}=frac{1}{100}cdot left( begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96 end{array} right)=
left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)
$$
Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.
Ответ: $A^{-1}=left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)$.
Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
Присоединённая (союзная, взаимная) матрица — матрица 
Из определения следует, что присоединённая матрица рассматривается только для квадратных матриц и сама является квадратной, так как понятие алгебраического дополнения вводится для квадратных матриц.

Исходная матрица:

Где:
— присоединённая (союзная, взаимная) матрица;
— алгебраические дополнения исходной матрицы;
— элементы исходной матрицы.
Эта матрица нужна для вычисления обратной матрицы:
где 

Обозначение[править | править код]
См. также[править | править код]
- Обратная матрица
- Алгебраическое дополнение
- Линейная алгебра
Литература[править | править код]
- Гантмахер Ф. Р. Теория матриц. — 2-е изд. — М.: Наука, 1966.
|
|
Это статья-заготовка по алгебре. Помогите Википедии, дополнив эту статью, как и любую другую. |
Как найти присоединенную матрицу
Найти присоединенную матрицу можно только для квадратной исходной матрицы, поскольку метод расчета подразумевает предварительное транспонирование. Это одна из операций в матричной алгебре, итогом которой является замена столбцов соответствующими строками. Кроме того, необходимо определить алгебраические дополнения.

Инструкция
Основой матричной алгебры являются операции над матрицами и поиск их основных характеристик. Чтобы найти присоединенную матрицу необходимо выполнить транспонирование и сформировать на основе ее результата новую матрицу из соответствующих алгебраических дополнений.
Транспонирование квадратной матрицы – это запись ее элементов в другом порядке. Первый столбец меняется на первую строку, второй – на вторую и т.д. в общем виде это выглядит так (см. рисунок).
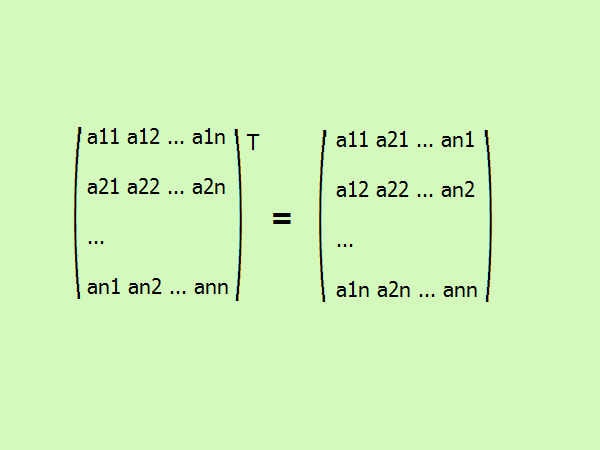
Второй этап нахождения присоединенной матрицы – поиск алгебраических дополнений. Эти числовые характеристики матричных элементов получаются путем вычисления миноров. Те, в свою очередь, являются определителями исходной матрицы порядка, меньшего на 1, и получаются вычеркиванием соответствующих строк и столбцов. Например, M11 = (a22•a33 – a23•a32). Алгебраическое дополнение отличается от минора коэффициентом, равным (-1) в степени суммы номеров элемента: A11 = (-1)^(1+1)• (a22•a33 – a23•a32).
Рассмотрите пример: найдите присоединенную матрицу к данной. Для удобства возьмем третий порядок. Это позволит быстрее понять алгоритм, не прибегая к тяжелым вычислениям, ведь для расчета определителей матрицы третьего порядка достаточно всего четырех элементов.
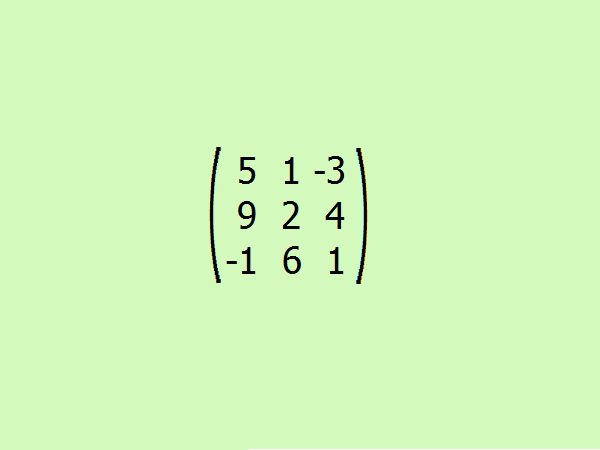
Проведите транспонирование заданной матрицы. Здесь требуется поменять местами первую строку на первый столбец, вторую – на второй и третью – на третий.
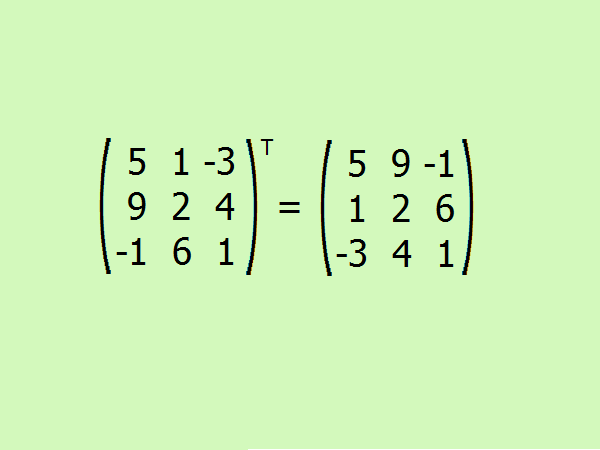
Запишите выражения для поиска алгебраических дополнений, всего их будет 9 по количеству элементов матрицы. Будьте внимательны со знаком, лучше воздержаться от расчетов в уме и расписать все подробно.
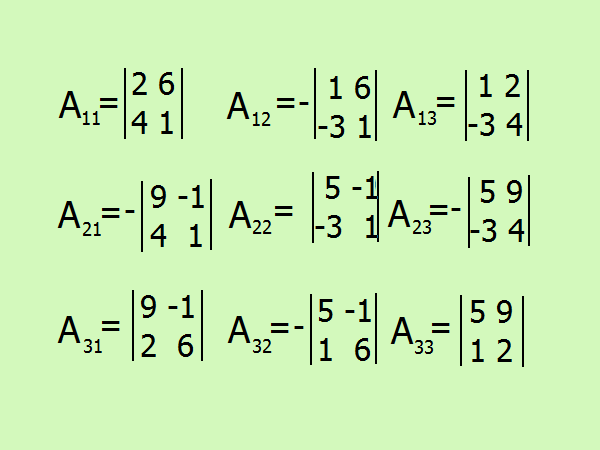
A11 = (-1)²•(2 -24) = -22;
A12 = (-1)³•(1+ 18) = -19;
A13 = (-1)^4•(4 + 6) = 10;
A21 = (-1)³•(9 + 4) = -13;
A22 = (-1)^4•(5 – 3) = 2;
A23 = (-1)^5•(20 + 27);
A31 = (-1)^4•(54 + 2) = 56;
A32 = (-1)^5•(30 + 1) = -31;
A33 = (-1)^6•(10 – 9) = 1.
Составьте итоговую присоединенную матрицу из получившихся алгебраических дополнений.
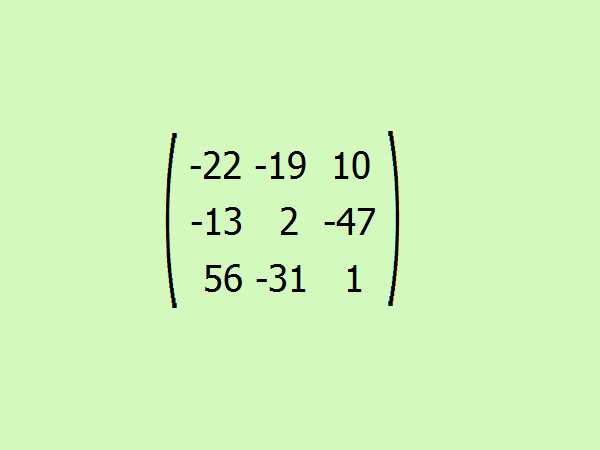
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как искать союзную матрицу?
Метод присоединённой (союзной) матрицы
- Найти определитель матрицы $A$ и убедиться, что $Delta Aneq 0$, т. …
- Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{ntimes n}^{*}=left(A_{ij} right)$ из найденных алгебраических дополнений.
Как вычислять обратные матрицы?
Другой алгоритм нахождения обратной матрицы
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
Как найти обратную матрицу с помощью присоединенной матрицы?
Нахождение обратной матрицы с помощью присоединённой матрицы Если к квадратной матрице дописать справа единичную матрицу того же порядка и с помощью элементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.
Как определить вырожденная матрица или нет?
Эквивалентные условия вырожденности
- Строки или столбцы матрицы линейно зависимы. …
- Квадратная матрица вырождена тогда и только тогда, когда существует ненулевой вектор такой, что …
- Квадратная матрица вырождена тогда и только тогда, когда у неё есть хотя бы одно нулевое собственное значение
Какую матрицу можно транспонировать?
Эрмитово-сопряженная матрица с комплексными элементами Рассмотрим комплексную матрицу. Элементы комплексной матрицы состоят из действительной и мнимой части. Такую матрицу также можно транспонировать, хотя в большинстве практических применений используют сопряженно-транспонированные, или эрмитово-сопряженные матрицы.
Когда матричное уравнение не имеет решения?
Тогда матричное уравнение запишется в виде: A·X = B. Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Как найти дельту в матрице?
Алгоритм нахождения определителя
- Для матриц порядка n=2 определитель вычисляется по формуле: Δ=a11*a22-a12*a21
- Для матриц порядка n=3 определитель вычисляется через алгебраические дополнения или методом Саррюса.
Как найти обратную матрицу с помощью метода Гаусса?
Получение обратной матрицы методом Гаусса относится к одному из точных (прямых) методов. Сначала записывается матрица, от которой необходимо найти обратную, а рядом с ней через черту записывается единичная диагональная матрица того же размера, вот так: ( 1 2 1 0 3 5 0 1 ) .
Чему равна единичная матрица?
Едини́чная ма́трица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.
Как найти определитель матрицы 3 на 3?
Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной …
Как найти дельту матрицы?
Алгоритм нахождения определителя
- Для матриц порядка n=2 определитель вычисляется по формуле: Δ=a11*a22-a12*a21
- Для матриц порядка n=3 определитель вычисляется через алгебраические дополнения или методом Саррюса.
Что такое размерность матрицы?
Определение 1. Матрицей размерности m×n называется прямоуголь- ная таблица чисел, содержащая m строк одинаковой длины (по n чисел в каждой строке) и n столбцов одинаковой длины (по m чисел в каждом столбце).
Какая матрица при Транспонировании не меняется?
При транспонировании матрицы ее определитель не меняется. 2. Если все элементы какого-либо столбца (строки) определителя равны нулю, то определитель также равен нулю. Это свойство очевидно, так как каждое слагаемое содержит по одному и только одному сомножителю из каждого столбца (строки).
В чем суть транспонирования матрицы?
Транспонирование матрицы Транспонированием матриц называется замена строк матрицы на её столбцы с сохранением порядка.
Что такое матричное уравнение?
Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.
Как решать матричный уравнения?
Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A-1. Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B . Если задано выражение A*X = B2 , то предварительно матрицу B надо возвести в квадрат.
Как найти детерминант матрицы 3 на 3?
Определитель матрицы 3×3 равен разности между суммой произведений элементов главной диагонали плюс произведение элементов лежащих на треугольниках, грань которых параллельна главной диагонали, и суммой произведений элементов побочной диагонали и элементов, лежащих на треугольниках с параллельной побочной диагонали …
Как найти обратную матрицу
- Быстрый способ для матриц $2 times 2$
- Пример 1
- Пример 2
- Нахождение с помощью метода Гаусса
- Пример 3
- Пример 4
- Метод союзной матрицы(алгебраические дополнения)
- Пример 5
Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.
Быстрый способ для матриц $2 times 2$
Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$
| Пример 1 |
| Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$. |
| Решение |
|
Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 – 4cdot5 = 27 – 20 = 7.$$ Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$ |
| Пример 2 |
| Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$. |
| Решение |
|
Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) – 4cdot(-1) = -12 + 4 = -8.$$ Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
Нахождение с помощью метода Гаусса
На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.
$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$
Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:
$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$
$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$
| Пример 3 |
| Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$ |
| Решение |
|
Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$ Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$ Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу. Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$ Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$ |
| Пример 4 |
| Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$ |
| Решение |
|
Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$ Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$ Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу. Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$ Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$ Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
| Ответ |
| $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
Метод союзной матрицы(алгебраические дополнения)
Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом
$$A^{-1} = frac{1}{|A|} (A^*)^T. $$
Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:
$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$
$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.
| Пример 5 |
| Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$ |
| Решение |
|
Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $ Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю: $$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 – 0 – 6 + 4 = 36 neq 0 $$ Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление. Вычеркиваем первую строку и первый столбец: $$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 – 2 = 10 $$ Убираем первую строку и второй столбец: $$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 – 0) = 4 $$ Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя. $$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 – 0 = 1 $$ $$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$ $$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 – 0 = 12 $$ $$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 – 0) = 3 $$ $$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 – 6 = -8 $$ $$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$ $$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$ Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений: $$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$ Транспонируем её и обозначаем $ (A^*)^T $: $$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ В итоге находим обратную матрицу $ A^{-1} $: $$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$ |






