Содержание:
Трение:
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения.
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка. Возникновение силы трения, препятствующей скольжению, иногда называют трением первого рода, а возникновение пары сил, препятствующей качению,— трением второго рода.
Трение скольжения
Пусть на тело действует плоская система активных сил и тело находится в равновесии, соприкасаясь с поверхностью другого тела, являющегося связью для рассматриваемого тела. Если поверхности соприкасающихся тел абсолютно гладкие и тела абсолютно твердые, то реакция поверхности связи направлена по нормали к общей касательной в точке соприкосновения и направление реакции в этом случае не зависит от действующих на тело активных сил. От активных сил зависит только числовое значение силы реакции. В действительности абсолютно гладких поверхностей и абсолютно твердых тел не бывает. Все поверхности тел в той или иной степени шероховаты и все тела деформируемы. В связи с этим и сила реакции 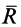
Если силу реакции 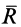
В теоретической механике обычно рассматривается только сухое трение между поверхностями тел, т. е. такое трение, когда между ними нет смазывающего вещества. Для сухого трения надо различать трение скольжения при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.
При покое сила трения зависит только от активных сил. При выбранном направлении касательной в точке соприкосновения поверхностей тел сила трения вычисляется по формуле
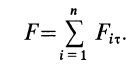
Аналогично, при выбранном направлении нормали нормальная реакция выражается через заданные силы
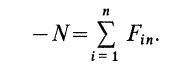
В 1781 г. Кулон установил основные приближенные законы для сухого трения скольжения. В дальнейшем законы Кулона многократно проверялись другими исследователями. Но эти законы подтверждались в случае, когда поверхности тел не вдавливались друг в друга и шероховатость была не очень велика.
Законы Кулона можно установить на приборе, схема которого дана рис. 59. На этом приборе изменяя вес гири, можно изменять нормальное давление 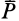 (или равную ему нормальную реакцию
(или равную ему нормальную реакцию 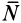 ) между трущимися поверхностями. Изменяя же вес гирь
) между трущимися поверхностями. Изменяя же вес гирь 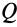 , можно изменять силу
, можно изменять силу 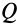 , которая стремится двигать тело вдоль поверхности другого тела, являющегося связью. Очевидно, что если сила
, которая стремится двигать тело вдоль поверхности другого тела, являющегося связью. Очевидно, что если сила 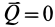 , то тело находится в равновесии и сила трения
, то тело находится в равновесии и сила трения 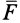 равна нулю.
равна нулю.
Если силу 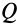 увеличить (при этом тело не скользит по поверхности, а находится в равновесии), то по условию равновесия возникает сила трения
увеличить (при этом тело не скользит по поверхности, а находится в равновесии), то по условию равновесия возникает сила трения 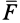 , которая равна, но противоположна активной силе
, которая равна, но противоположна активной силе 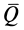 . Нормальная реакция
. Нормальная реакция 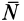 равна нормальному давлению
равна нормальному давлению 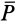 . Увеличивая силу
. Увеличивая силу 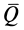 при одном и том же нормальном давлении
при одном и том же нормальном давлении 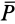 , можно достичь и такого положения, когда ничтожно малое дальнейшее увеличение силы
, можно достичь и такого положения, когда ничтожно малое дальнейшее увеличение силы 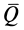 выведет тело из равновесия, заставляя его скользить по поверхности связи. Очевидно, будет достигнуто предельное положение, при котором сила трения станет наибольшей и не сможет уравновешивать силу
выведет тело из равновесия, заставляя его скользить по поверхности связи. Очевидно, будет достигнуто предельное положение, при котором сила трения станет наибольшей и не сможет уравновешивать силу 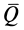 при ее дальнейшем увеличении. Изменяя силу нормального давления
при ее дальнейшем увеличении. Изменяя силу нормального давления 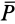 , можно исследовать, как изменяется при этом предельная сила трения
, можно исследовать, как изменяется при этом предельная сила трения 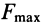 . Можно также исследовать влияние на предельную силу трения площади соприкосновения тел, сохраняя при этом нормальное давление, а также влияние материала тел, характер обработки поверхностей и другие факторы. Такие опыты позволяют проверить законы Кулона для сухого трения скольжения.
. Можно также исследовать влияние на предельную силу трения площади соприкосновения тел, сохраняя при этом нормальное давление, а также влияние материала тел, характер обработки поверхностей и другие факторы. Такие опыты позволяют проверить законы Кулона для сухого трения скольжения.
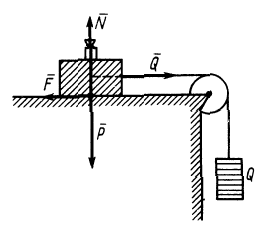
Рис. 59
Трение скольжения:
При решении многих технических вопросов приходится принимать в расчет силы трения. Остановимся на рассмотрении сил трения 1-го рода (скольжения).
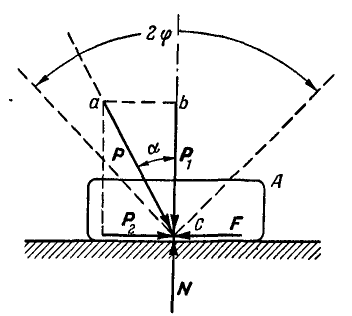
Рис. 31.
Пусть на тело А (рис. 31), лежащее на горизонтальной негладкой плоскости, действует сила Р под углом а к вертикали. Раскладывая силу Р на две составляющие 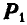 и
и 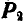 замечаем, что сила
замечаем, что сила 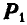 уравновешивается с реакцией плоскости N; вторая же составляющая
уравновешивается с реакцией плоскости N; вторая же составляющая 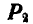 неминуемо должна была бы сообщить телу А движение вправо, но при небольшом угле α тело А находится еще в покое; следовательно, в противоположную сторону силы
неминуемо должна была бы сообщить телу А движение вправо, но при небольшом угле α тело А находится еще в покое; следовательно, в противоположную сторону силы 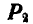 направлено сопротивление, которое обусловлено силой трения F. Увеличивая постепенно угол будет возрастать до некоторого предела. Обозначим через
направлено сопротивление, которое обусловлено силой трения F. Увеличивая постепенно угол будет возрастать до некоторого предела. Обозначим через 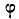 угол, при котором начинается скольжение тела по плоскости. В этом случае сила трения достигает наибольшей величины; определяем ее из Δabc при
угол, при котором начинается скольжение тела по плоскости. В этом случае сила трения достигает наибольшей величины; определяем ее из Δabc при  по формуле:
по формуле:
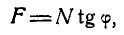
где 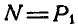 — нормальная реакция плоскости.
— нормальная реакция плоскости.
Угол 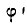 называется углом трения, а тангенс этого угла — коэффициентом трения скольжения и обозначается через f; следовательно, вообще:
называется углом трения, а тангенс этого угла — коэффициентом трения скольжения и обозначается через f; следовательно, вообще:
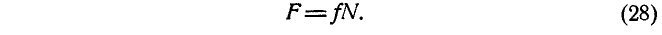
Формула (28) выражает первый закон трения, который формулируется так:
Первый закон трения
1. Сила трения прямо пропорциональна нормальному давлению или реакции связи и направлена в сторону, противоположную относительному перемещению трущихся тел.
Этот закон был установлен опытным путем. Амонтоном-Кулоном и другими исследователями были установлены еще следующие законы:
2. Коэффициент трения зависит от материала и состояния трущихся поверхностей.
3. Коэффициент трения в покое больше коэффициента трения в движении.
4. Коэффициент трения не зависит от величины трущихся поверхностей (можно считать правильным лишь в первом приближении).
5. Коэффициент трения зависит от скорости движения трущихся поверхностей и с увеличением этой скорости уменьшается, приближаясь к некоторой предельной величине.
Обращаясь к рисунку 31, замечаем, что тело А находится в равновесии, если сила Р проходит внутри конуса с углом при вершине С, равным двойному углу трения 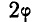 ; такой конус называется конусом трения и играет важную роль при решении задач.
; такой конус называется конусом трения и играет важную роль при решении задач.
Когда тело А находится еще в покое (рис. 31), то по мере увеличения угла 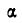 возрастает также и сила
возрастает также и сила 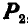 , а сила F уменьшается. Наконец, наступает такой момент, когда при
, а сила F уменьшается. Наконец, наступает такой момент, когда при 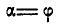 тело находится на грани между покоем и скольжением. В этом случае сила F и коэффициент трения в покое f достигают наибольшего значения. При незначительном увеличении силы
тело находится на грани между покоем и скольжением. В этом случае сила F и коэффициент трения в покое f достигают наибольшего значения. При незначительном увеличении силы 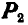 тело А начинает скользить по плоскости, благодаря чему нарушается сцепление между поверхностями соприкасания тела и плоскости. В этом случае сила трения скольжения F коэффициент трения в движении f уменьшаются по величине, приближаясь к некоторой предельной величине с увеличением относительной скорости скольжения. Исключение составляют лишь некоторые’материалы, например при трении кожи о металл в ременных передачах, где с увеличением скорости относительного скольжения коэффициент трения также возрастает.
тело А начинает скользить по плоскости, благодаря чему нарушается сцепление между поверхностями соприкасания тела и плоскости. В этом случае сила трения скольжения F коэффициент трения в движении f уменьшаются по величине, приближаясь к некоторой предельной величине с увеличением относительной скорости скольжения. Исключение составляют лишь некоторые’материалы, например при трении кожи о металл в ременных передачах, где с увеличением скорости относительного скольжения коэффициент трения также возрастает.
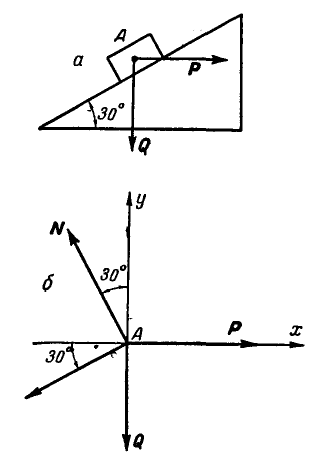
Рис. 32.
Задача №1
Тело А весом Q=100кГ лежит на шероховатой наклонной плоскости (рис. 32,а). Какую наименьшую горизонтальную силу Р ладо приложить к телу, чтобы оно начало двигаться, если коэффициент трения тела о плоскость f=0,2.
Решение. Рассмотрим равновесие тела А. Помимо горизонтальной силы Р на тело действует сила Q, нормальная реакция N плоскости и сила трения F, направленная параллельно плоскости в обратную сторону движения тела (рис. 32,6).
Составляя уравнения равновесия (27), имеем:
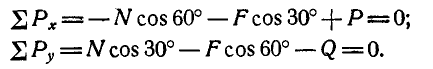
В двух уравнениях имеются три неизвестные величины: Р, N и F. Для получения третьего уравнения по формуле (28) имеем > зависимость: 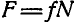 .
.
Выражая в уравнениях равновесия F через N, получим:
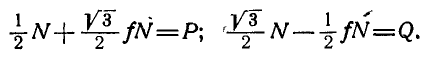
Оторда находим: 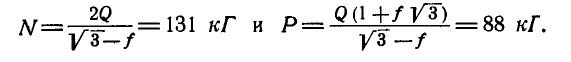
Задача №2
Определить наибольший и наименьший груз Р, при котором груз Q = 10 кГ не будет двигаться (рис» 33, а). Коэффициент трения груза Q о плоскость f=0,2.
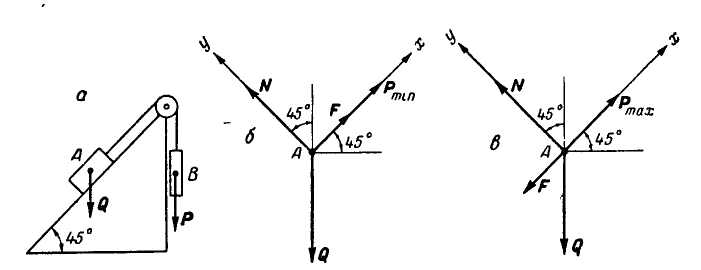
Рис. 33.
Указание: при наименьшем грузе 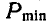 тело А будет стремиться сползти вниз, следовательно сила трения F будет направлена параллельно плоскости вверх (рис. 33, б). При наибольшем грузе
тело А будет стремиться сползти вниз, следовательно сила трения F будет направлена параллельно плоскости вверх (рис. 33, б). При наибольшем грузе 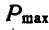 , напротив, тело А стремится двигаться кверху, а потому сила трения F будет направлена параллельно плоскости вниз (рис. 33, в).
, напротив, тело А стремится двигаться кверху, а потому сила трения F будет направлена параллельно плоскости вниз (рис. 33, в).
Составляя для каждого из случаев (рис. 33, б и 33, в) по два уравнения равновесия и принимая во внимание формулу (28), получим:
32
Законы Кулона
1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного или реального скольжения тела под действием приложенных сил. Сила трения при покое зависит от активных сил и ее модуль заключен между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, т. е.
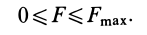
2. Максимальная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того, чтобы сдвинуть, например, кирпич, надо приложить одну и ту же силу независимо от того, какой гранью он положен на поверхность, широкой или узкой.
3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции), т. е.

где безразмерный коэффициент 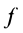 называют коэффициентом трения скольжения; он не зависит от нормального давления.
называют коэффициентом трения скольжения; он не зависит от нормального давления.
4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, т. е. от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения скольжения в зависимости от различных условий устанавливается экспериментально. Так, коэффициент трения для кирпича по бетону равен 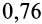 ; для стали по стали —
; для стали по стали — 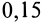 ; для дуба по дубу поперек волокон —
; для дуба по дубу поперек волокон — 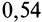 , а для дуба по дубу вдоль волокон —
, а для дуба по дубу вдоль волокон — 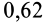 .
.
Опыты показывают, что при скольжении одного тела по поверхности другого с некоторой относительной скоростью возникает сила трения скольжения, равная максимальной, только при этом коэффициент трения скольжения незначительно изменяется в зависимости от скорости скольжения. Для большинства материалов он уменьшается с увеличением скорости скольжения, но для некоторых материалов, наоборот, увеличивается (трение кожи о металл).
В приближенных технических расчетах обычно считают, что коэффициент трения скольжения не зависит от относительной скорости скольжения.
В отличие от сухого трения трение при наличии смазывающего слоя между поверхностями определяется распределением относительной скорости скольжения в этом слое. В этом случае трение происходит не между поверхностями тел, а между слоями смазывающего вещества. Теория трения в смазывающем слое жидкости рассматривается в гидродинамике.
Угол и конус трения
Многие задачи на равновесие тела на шероховатой поверхности, т. е. при наличии силы трения, удобно решать геометрически. Для этой цели введем понятия угла и конуса трения.
Пусть твердое тело под действием активных сил находится на шероховатой поверхности в предельном состоянии равновесия, т. е. таком состоянии, когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции (рис. 60). В этом случае полная реакция шероховатой поверхности 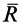 отклонена от нормали общей касательной плоскости трущихся поверхностей на наибольший угол.
отклонена от нормали общей касательной плоскости трущихся поверхностей на наибольший угол.
Этот наибольший угол 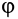 между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции, и направлением нормальной реакции называют углом трения.
между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции, и направлением нормальной реакции называют углом трения.
Угол трения 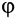 зависит от коэффициента трения, т. е.
зависит от коэффициента трения, т. е.
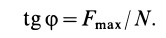
Но по третьему закону Кулона,
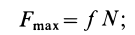
следовательно,

т. е. тангенс угла трения равен коэффициенту трения.
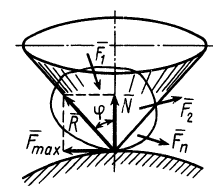
Рис. 60
Конусом трения называют конус, описанный полной реакцией, построенной на максимальной силе трения, вокруг направления нормальной реакции. Его можно получить изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся поверхностей.
Если коэффициент трения во всех направлениях одинаков, то конус трения круговой. Если не одинаков, то конус трения не круговой, например в случае, когда свойства соприкасающихся поверхностей различны (вследствие определенного направления волокон или в зависимости от направления обработки поверхности тел, если обработка происходит на строгальном станке и т. п.).
Равновесие тела на шероховатой поверхности
При равновесии сил, действующих на твердое тело, находящееся в равновесии на шероховатой поверхности, возникает дополнительно неизвестная сила реакции шероховатой поверхности— сила трения. В случае предельного равновесия сила трения достигает своего максимального значения и по формуле (1) выражается через нормальную реакцию. В общем случае равновесия сила трения находится между нулем и ее максимальным значением. Поэтому соответствующие условия равновесия, в которые входит сила трения после замены ее максимальным значением, становятся неравенствами. После этого неизвестные находят путем совместного решения уравнений и неравенств. Для всех неизвестных или для их части получают решения в виде неравенств.
Некоторые задачи на равновесие с учетом сил трения удобно решать геометрически с помощью конуса трения.
Можно сформулировать условия равновесия тела на шероховатой поверхности используя конус трения. Если активные силы, действующие на тело, приводятся к равнодействующей силе 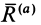 , то при равновесии тела на шероховатой поверхности равнодействующая активных сил
, то при равновесии тела на шероховатой поверхности равнодействующая активных сил 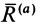 по аксиоме о равновесии двух сил, приложенных к твердому телу, уравновешивается полной реакцией R шероховатой поверхности (рис. 61). Полная реакция проходит через вершину конуса, а следовательно, через вершину конуса проходит и равнодействующая активных сил.
по аксиоме о равновесии двух сил, приложенных к твердому телу, уравновешивается полной реакцией R шероховатой поверхности (рис. 61). Полная реакция проходит через вершину конуса, а следовательно, через вершину конуса проходит и равнодействующая активных сил.
Очевидно, при изменении равнодействующей активных сил тело находится в равновесии до тех пор, пока составляющая 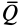 равнодействующей активных сил, лежащая в общей касательной плоскости соприкасающихся поверхностей не будет превышать наибольшего значения силы трения
равнодействующей активных сил, лежащая в общей касательной плоскости соприкасающихся поверхностей не будет превышать наибольшего значения силы трения 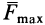 .
.
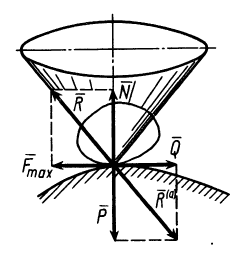
Рис. 61
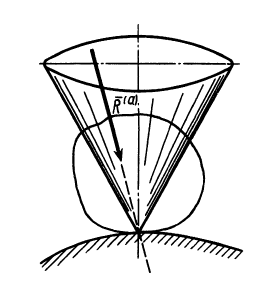
Рис. 62
Предельным положением равновесия тела является случай, когда сила 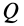 равна силе
равна силе 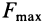 . В этом случае равнодействующая активных сил
. В этом случае равнодействующая активных сил 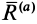 направлена по образующей конуса трения, так как
направлена по образующей конуса трения, так как 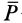 —составляющая равнодействующей активных сил по нормали — уравновешена нормальной реакцией
—составляющая равнодействующей активных сил по нормали — уравновешена нормальной реакцией 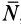 , если только активные силы не отделяют тела от шероховатой поверхности. Поэтому условие равновесия тела на шероховатой поверхности можно сформулировать так: для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину (рис. 62).
, если только активные силы не отделяют тела от шероховатой поверхности. Поэтому условие равновесия тела на шероховатой поверхности можно сформулировать так: для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину (рис. 62).
Тело нельзя вывести из равновесия любой по модулю активной силой, если ее линия действия проходит внутри конуса трения.
Если линия действия равнодействующей активных сил не проходит внутри конуса трения или по его образующей, то тело на шероховатой поверхности не может находиться в равновесии (рис. 63).
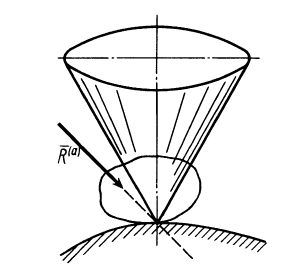
Рис. 63
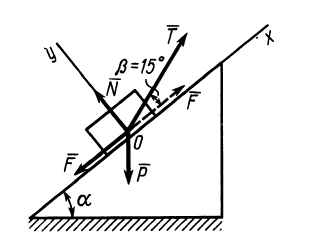
Рис. 64
Пример 1.
Тело, сила тяжести которого 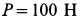 , удерживается в равновесии силой
, удерживается в равновесии силой 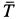 на шероховатой наклонной плоскости, имеющей угол наклона
на шероховатой наклонной плоскости, имеющей угол наклона 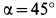 (рис. 64). Коэффициент трения скольжения между телом и плоскостью
(рис. 64). Коэффициент трения скольжения между телом и плоскостью 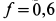 . Сила
. Сила 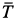 действует на тело под углом
действует на тело под углом 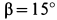 к линии наибольшего ската. Определить значение силы
к линии наибольшего ската. Определить значение силы 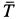 при равновесии тела на шероховатой наклонной плоскости.
при равновесии тела на шероховатой наклонной плоскости.
Решение. К телу приложены силы 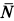 ,
, 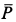 ,
, 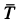 и сила трения
и сила трения 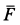 . Возможны два случая предельного равновесия тела и соответственно два предельных значения силы
. Возможны два случая предельного равновесия тела и соответственно два предельных значения силы 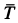 при двух направлениях силы трения по наклонной плоскости вниз и вверх в зависимости от направления возможного скольжения вверх по наклонной плоскости и вниз. Для составления уравнений равновесия целесообразно ввести
при двух направлениях силы трения по наклонной плоскости вниз и вверх в зависимости от направления возможного скольжения вверх по наклонной плоскости и вниз. Для составления уравнений равновесия целесообразно ввести 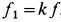 , где
, где 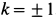 .
.
Составляем условия равновесия в виде суммы проекций сил на координатные оси для обоих предельных случаев. Имеем

По закону Кулона,
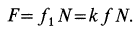
Решая эти уравнения относительно 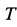 , получаем
, получаем
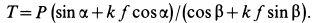
Отсюда при 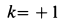
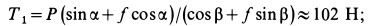
при 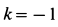
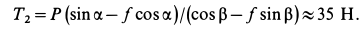
Таким образом, сила 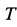 при равновесии тела должна удовлетворять условию
при равновесии тела должна удовлетворять условию 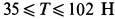 .
.
Пример 2.
Однородный тяжелый стержень 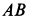 длиной
длиной 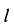 опирается концом
опирается концом 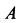 на гладкую вертикальную стену, а другим
на гладкую вертикальную стену, а другим 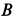 — на шероховатую вертикальную стену (рис.65). Расстояние между стенами
— на шероховатую вертикальную стену (рис.65). Расстояние между стенами 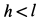 . Определить коэффициент трения стены
. Определить коэффициент трения стены 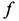 , при котором возможно равновесие стержня.
, при котором возможно равновесие стержня.
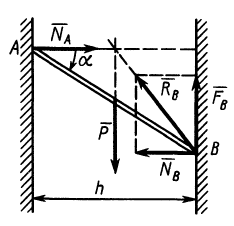
Рис. 65
Решение. Рассмотрим случай, когда точка 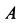 расположена выше точки
расположена выше точки 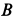 стержня. Равновесие стержня невозможно, если точка
стержня. Равновесие стержня невозможно, если точка 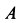 расположена ниже точки
расположена ниже точки 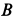 . На стержень действуют сила тяжести
. На стержень действуют сила тяжести 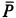 , приложенная посередине стержня нормальная реакция гладкой стены
, приложенная посередине стержня нормальная реакция гладкой стены 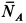 и реакция шероховатой стены
и реакция шероховатой стены 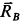 , которую разложим на нормальную реакцию
, которую разложим на нормальную реакцию 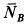 и силу трения
и силу трения 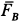 .
.
Составим условия равновесия плоской системы сил:
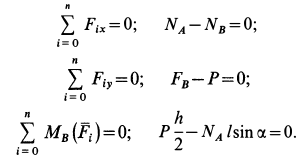
К этим условиям следует добавить неравенство для силы трения
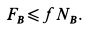
Из уравнений равновесия находим
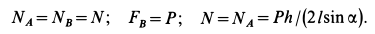
Из геометрических условий задачи имеем
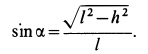
Итак, для силы трения 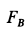 имеем следующие уравнение и неравенство:
имеем следующие уравнение и неравенство:
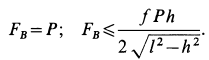
Исключая из них силу трения 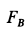 , после сокращения на
, после сокращения на 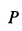 получаем
получаем
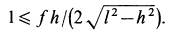
Искомое условие для коэффициента трения 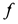 при равновесии стержня принимает вид
при равновесии стержня принимает вид
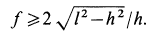
Трение качения
Если рассматриваемое тело имеет форму катка и под действием приложенных активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте соприкосновения могут возникнуть силы реакции, препятствующие не только скольжению, но и качению. Примерами таких катков являются различные колеса, как, например, у электровозов, вагонов, автомашин, шарики и ролики в шариковых и роликовых подшипниках и т. п.
Пусть цилиндрический каток находится на горизонтальной плоскости под действием активных сил. Соприкосновение катка с плоскостью из-за деформации фактически происходит не вдоль одной образующей, как в случае абсолютно твердых тел, а по некоторой площадке. Если активные силы приложены симметрично относительно среднего сечения катка, т. е. вызывают одинаковые деформации вдоль всей его образующей, то можно изучать только одно среднее сечение катка. Этот случай рассмотрен ниже.
Активные силы, действующие на катки в виде колес (рис. 66), кроме силы тяжести 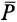 обычно состоят из силы
обычно состоят из силы 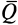 , приложенной к центру колеса параллельно общей касательной в точке
, приложенной к центру колеса параллельно общей касательной в точке 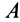 , и пары сил с моментом
, и пары сил с моментом 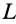 , стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если
, стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если 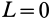 , а
, а 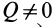 то колесо называют ведомым-, если
то колесо называют ведомым-, если 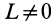 , a
, a 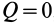 , то ведущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда.
, то ведущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда.
Если активные силы, действующие на колесо, привести к точке 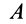 соприкосновения катка с плоскостью, у которых нет деформации, то в общем случае получим силу и пару сил, стремящиеся заставить каток скользить и катиться. Следует различать чистое качение, когда точка соприкосновения
соприкосновения катка с плоскостью, у которых нет деформации, то в общем случае получим силу и пару сил, стремящиеся заставить каток скользить и катиться. Следует различать чистое качение, когда точка соприкосновения 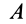 катка не скользит по неподвижной плоскости, и качение со скольжением, когда наряду с вращением катка есть и скольжение, т. е. точка
катка не скользит по неподвижной плоскости, и качение со скольжением, когда наряду с вращением катка есть и скольжение, т. е. точка 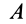 катка движется по плоскости. При чистом скольжении, наоборот, каток движется по плоскости, не имея вращения.
катка движется по плоскости. При чистом скольжении, наоборот, каток движется по плоскости, не имея вращения.
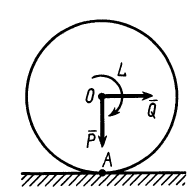
Рис. 66
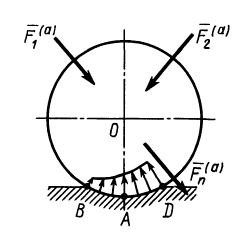
Рис. 67
Рис. 68
Соприкосновение среднего сечения колеса с неподвижной плоскостью из-за деформации колеса и плоскости происходит по некоторой линии 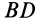 . По этой линии на колесо действуют распределенные силы реакции (рис. 67). Если привести распределенные силы к точке
. По этой линии на колесо действуют распределенные силы реакции (рис. 67). Если привести распределенные силы к точке 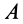 , то в этой точке получим главный вектор
, то в этой точке получим главный вектор 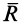 этих распределенных сил с составляющими
этих распределенных сил с составляющими 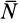 (нормальная реакция) и
(нормальная реакция) и 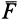 (сила трения скольжения), а также пару сил с моментом
(сила трения скольжения), а также пару сил с моментом 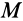 . При симметричном распределении сил по линии
. При симметричном распределении сил по линии 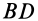 относительно точки
относительно точки 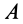 момент
момент 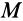 пары сил равен нулю. В этом случае нет активных сил, стремящихся катить каток в каком-либо направлении. _
пары сил равен нулю. В этом случае нет активных сил, стремящихся катить каток в каком-либо направлении. _
Приведем активные силы 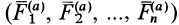 в общем случае к точке
в общем случае к точке 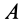 . В этой точке получим главный вектор этих сил
. В этой точке получим главный вектор этих сил 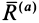 и пару сил, момент которой равен главному моменту
и пару сил, момент которой равен главному моменту 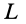 (рис. 68).
(рис. 68).
При равновесии катка, т. е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,
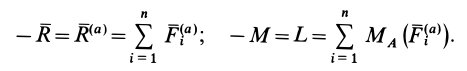
Изменив активные силы, приложенные к катку так, чтобы увеличивался момент 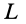 пары активных сил, стремящейся катить каток. Пока каток находится в равновесии, увеличивается и равный ему по числовой величине, но противоположный по направлению момент
пары активных сил, стремящейся катить каток. Пока каток находится в равновесии, увеличивается и равный ему по числовой величине, но противоположный по направлению момент 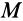 пары сил, препятствующий качению катка и возникающий от действия на каток неподвижной плоскости. Наибольшее значение
пары сил, препятствующий качению катка и возникающий от действия на каток неподвижной плоскости. Наибольшее значение 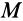 достигается в момент начала качения катка по плоскости.
достигается в момент начала качения катка по плоскости.
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:
1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента 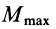 пропорционально нормальному давлению, а следовательно, и равной ему нормальной реакции
пропорционально нормальному давлению, а следовательно, и равной ему нормальной реакции 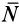 :
:

Коэффициент пропорциональности 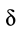 называют коэффициентом трения качения при покое или коэффициентом трения второго рода. Из формулы (3) следует, что
называют коэффициентом трения качения при покое или коэффициентом трения второго рода. Из формулы (3) следует, что 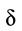 имеет размерность длины.
имеет размерность длины.
3. Коэффициент трения качения 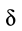 зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости. Для случая качения вагонного колеса по стальному рельсу коэффициент трения качения
зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости. Для случая качения вагонного колеса по стальному рельсу коэффициент трения качения 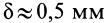 .
.
Законы трения качения, как и законы трения скольжения, справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов катка и плоскости.
Эти законы позволяют не рассматривать деформации катка и плоскости, считая их абсолютно твердыми телами, касающимися в одной точке. В этой точке соприкосновения в среднем сечении катка кроме нормальной реакции и силы трения надо приложить еще и пару сил, препятствующую качению.
Коэффициент трения качения равен длине 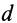 , которую вычислим следующим образом. Сложим нормальную реакцию
, которую вычислим следующим образом. Сложим нормальную реакцию 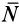 с парой сил, препятствующей качению в момент, когда
с парой сил, препятствующей качению в момент, когда 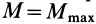 . Получим ту же силу
. Получим ту же силу 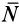 , но сдвинутую параллельно самой себе на расстояние
, но сдвинутую параллельно самой себе на расстояние
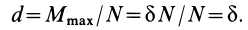
В предельном случае равновесия катка 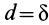 . Эту величину следует отложить в направлении, в котором активные силы стремятся катить каток (рис. 69).
. Эту величину следует отложить в направлении, в котором активные силы стремятся катить каток (рис. 69).
Для того чтобы каток не скользил, необходимо выполнение условия

Для заданных активных сил соответственно
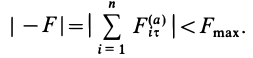
Для того чтобы каток не катился, должно выполняться условие

Для активных сил оно имеет вид
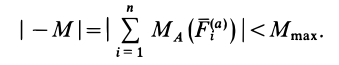
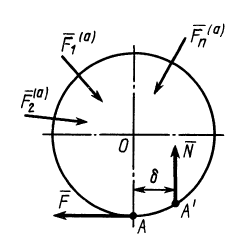
Рис. 69
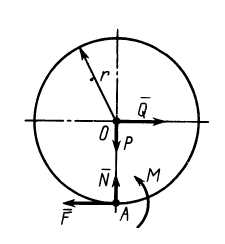
Рис. 70
Для примера рассмотрим случай ведомого колеса, к которому кроме силы тяжести 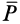 приложена еще горизонтальная активная сила
приложена еще горизонтальная активная сила 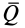 (рис. 70).
(рис. 70).
Если каток находится в равновесии, то из условий равновесия плоской системы сил, приложенных к катку, получаем
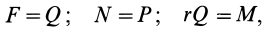
где за моментную точку взята точка 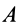 .
.
В случае отсутствия скольжения по формуле (4) с учетом условий равновесия
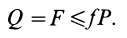
Аналогично, при отсутствии качения по формуле (5) имеем
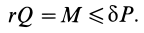
Таким образом, при отсутствии скольжения сила 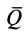 должна удовлетворять условию
должна удовлетворять условию 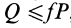 , а при отсутствии качения эта же сила
, а при отсутствии качения эта же сила 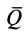 — удовлетворять другому условию:
— удовлетворять другому условию:
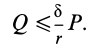
Если 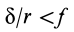 , то, пока
, то, пока 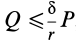 , каток находится в равновесии.
, каток находится в равновесии.
Если 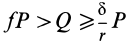 , то каток катится без скольжения (чистое качение). При
, то каток катится без скольжения (чистое качение). При 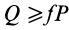 кроме качения появляется еще и скольжение. При
кроме качения появляется еще и скольжение. При 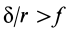 каток находится в равновесии, пока
каток находится в равновесии, пока 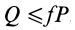 . Если
. Если 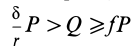 , он скользит не вращаясь (поступательное движение). При
, он скользит не вращаясь (поступательное движение). При 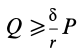 наряду со скольжением возникает качение.
наряду со скольжением возникает качение.
В том случае, если 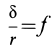 , каток находится в равновесии, пока
, каток находится в равновесии, пока 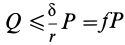 . Если же
. Если же 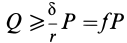 , то он катится со скольжением.
, то он катится со скольжением.
Обычно 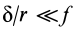 и, следовательно, для начала качения катка требуется значительно меньшая сила
и, следовательно, для начала качения катка требуется значительно меньшая сила 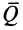 , чем для начала его скольжения. Поэтому по мере увеличения силы
, чем для начала его скольжения. Поэтому по мере увеличения силы 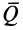 каток сначала начинает катиться, а при дальнейшем ее росте к качению добавляется еще и скольжение.
каток сначала начинает катиться, а при дальнейшем ее росте к качению добавляется еще и скольжение.
С точки зрения затраты энергии выгодно заменять скольжение качением. Этим объясняется преимущество шариковых и роликовых подшипников по сравнению с подшипниками скольжения, если даже в них трение и не уменьшается введением смазывающего вещества.
Аналогично трению качения можно рассмотреть и явление возникновения так называемого трения верчения, т.е. случая, когда активные силы стремятся вращать тело, например в форме шара, вокруг нормали к общей касательной поверхности соприкосновения.
В этом случае возникает пара сил, препятствующая верчению, причем наибольший ее момент, возникающий в момент начала верчения, также прямо пропорционален нормальной реакции. Коэффициент пропорциональности, т. е. коэффициент трения верчения, обычно значительно меньше коэффициента трения качения.
Равновесие с учетом сил трения
Задачи, приведенные в этом параграфе, отличаются от предыдущих тем, что в них рассматривается равновесие тел, имеющих, кроме идеальных, еще и реальные связи, т. е. связи с трением.
При свободном опирании тела на поверхность идеальной связи реакция такой связи 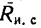 (рис. 117, а) направлена перпендикулярно к ее поверхности, т. е. по нормали п к этой поверхности.
(рис. 117, а) направлена перпендикулярно к ее поверхности, т. е. по нормали п к этой поверхности.
Если же тело опирается на поверхность реальной связи (в отличие от идеальных связей реальные связи условимся отмечать двойной штриховкой), то ее реакция 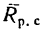 (рис. 117,6)в зависимости от нагрузок, приложенных к телу, отклонится от нормали п к поверхности связи на некоторый угол
(рис. 117,6)в зависимости от нагрузок, приложенных к телу, отклонится от нормали п к поверхности связи на некоторый угол 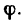
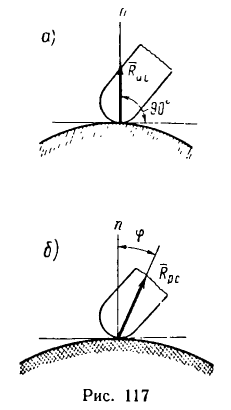
Поясним это общее положение следующим примером.
Наклонный брус (рис. 118, а), вес которого G, опирается в двух
точках А и В соответственно на вертикальную и горизонтальную поверхности идеальных связей. Этот брус не может находиться в равновесии, потому что три силы —вес бруса G и реакции 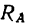 и
и 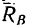 —расположены так, что не выполняется необходимое условие равновесия трех непараллельных сил; их линии действия не пересекаются в одной точке.
—расположены так, что не выполняется необходимое условие равновесия трех непараллельных сил; их линии действия не пересекаются в одной точке.
Чтобы брус, показанный на рис. 118, а, находился в равновесии, необходимо наложить еще одну связь, например, удержать брус шнуром или упереть в выступ на горизонтальной плоскости (обе возможные связи показаны пунктиром).
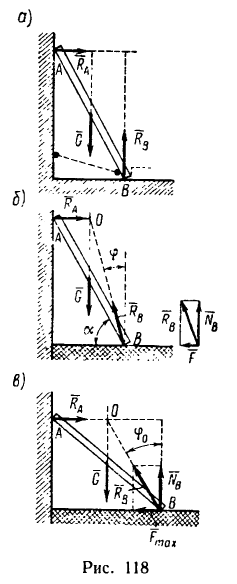
Теперь представим, что в точке В брус опирается не на идеально гладкую, а на шероховатую (реальную) поверхность (рис 118, б). В этом случае брус может находиться в равновесии без дополнительной связи (шнура или упорной планки). Значит три силы — вес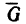 и реакции опор
и реакции опор 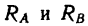 — образуют уравновешенную систему. Равновесие трех сил, действующих на брус, возможно потому, что реакция
— образуют уравновешенную систему. Равновесие трех сил, действующих на брус, возможно потому, что реакция 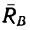 реальной связи отклоняется на некоторый угол
реальной связи отклоняется на некоторый угол 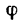 от нормали к поверхности связи и линии действия всех трех сил пересекаются в точке О.
от нормали к поверхности связи и линии действия всех трех сил пересекаются в точке О.
Если реакцию 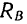 реальной связи разложим на две составляющие, направленные вдоль поверхности и перпендикулярно к ней (это разложение показано на рис. 118, а справа), то получим силу
реальной связи разложим на две составляющие, направленные вдоль поверхности и перпендикулярно к ней (это разложение показано на рис. 118, а справа), то получим силу 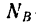 —нормальную составляющую
—нормальную составляющую 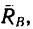 , численно равную нормальному давлению, производимому концом бруса на опору, и силу F—касательную составляющую реакции
, численно равную нормальному давлению, производимому концом бруса на опору, и силу F—касательную составляющую реакции 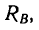 которая называется силой трения.
которая называется силой трения.
При увеличении угла а, характеризующего наклон бруса относительно горизонтальной поверхности, угол 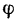 уменьшается, а вместе с ним уменьшается и сила трения, но брус сохраняет равновесие.
уменьшается, а вместе с ним уменьшается и сила трения, но брус сохраняет равновесие.
Если же уменьшать угол а, то угол ф, характеризующий отклонение реакции 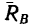 от нормали, увеличивается, а вместе с ним увеличивается и сила трения (рис. 118, в). При некотором наклоне бруса, определенном для данной пары соприкасающихся в точке В тел (например, для деревянного бруса, опирающегося о деревянный пол), брус скользит. Это означает, что сила трения, достигая предельного значения, больше увеличиваться не может. При этом реакция отклоняется также до предельного значения
от нормали, увеличивается, а вместе с ним увеличивается и сила трения (рис. 118, в). При некотором наклоне бруса, определенном для данной пары соприкасающихся в точке В тел (например, для деревянного бруса, опирающегося о деревянный пол), брус скользит. Это означает, что сила трения, достигая предельного значения, больше увеличиваться не может. При этом реакция отклоняется также до предельного значения 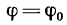 и при дальнейшем уменьшении угла а линия действия реакции
и при дальнейшем уменьшении угла а линия действия реакции 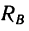 уже не попадает в точку пересечения сил G и
уже не попадает в точку пересечения сил G и 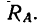
У гол 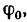 соответствующий
соответствующий 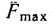 максимальному значению силы трения, называется углом трения. Числовое значение угла трения зависит от материала соприкасающихся тел и от состояния их поверхностей.
максимальному значению силы трения, называется углом трения. Числовое значение угла трения зависит от материала соприкасающихся тел и от состояния их поверхностей.
Для случая предельного равновесия между силой трения и углом трения имеем такую зависимость;
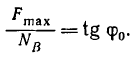
Постоянное для данной пары соприкасающихся тел значение 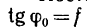 называется коэффициентом трения при покое.
называется коэффициентом трения при покое.
Таким образом,
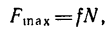
При решении задач необходимо учитывать, что сила трения направлена всегда в сторону, противоположную той, при которой точка может скользить по идеальной поверхности.
Если в число реакций связей, обеспечивающих равновесие тела, входит сила трения, то такое состояние равновесия называется самоторможением. Во всех приведенных ниже задачах рассмотрены различные случаи самоторможения (равновесия при наличии силы трения) и условия, при которых возможно самоторможение.
Задача №3
Тело А массой 8 кг поставлено на шероховатую горизонтальную поверхность стола. К телу привязана нить, перекинутая через блок Б (рис. 119, а). Какой груз Р можно подвязать к концу нити, свешивающейся с блока, чтобы не нарушить равновесия тела А? Коэффициент трения f = 0,4. Трением на блоке пренебречь.
Решение.
1. Если масса тела А m = 8 кг, то его вес
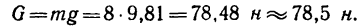
2. Пренебрегая размерами тела, будем считать, что все силы приложены к точке А.
3. Когда тело поставлено на горизонтальную поверхность, то на него действуют только две силы: вес 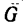 и противоположно направленная реакция опоры
и противоположно направленная реакция опоры 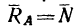 (рис. 119,6).
(рис. 119,6).
4. Если же приложить некоторую силу 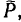 действующую вдоль горизонтальной поверхности, то реакция
действующую вдоль горизонтальной поверхности, то реакция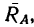 уравновешивающая силы
уравновешивающая силы 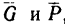 начнет отклоняться от вертикали, но тело А будет находиться в равновесии до тех пор, пока модуль силы Р не превысит максимального значения силы трения F, соответствующей предельному значению угла
начнет отклоняться от вертикали, но тело А будет находиться в равновесии до тех пор, пока модуль силы Р не превысит максимального значения силы трения F, соответствующей предельному значению угла 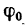 (рис. 119, в).
(рис. 119, в).
5. Разложив реакцию 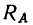 на две составляющие
на две составляющие 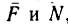 получаем систему четырех сил, приложенных к одной точке (рис. 119, г).
получаем систему четырех сил, приложенных к одной точке (рис. 119, г).
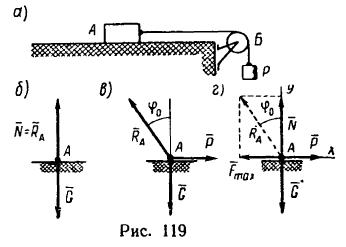
Спроектировав эту систему сил на оси хну, получим два уравнения равновесия:
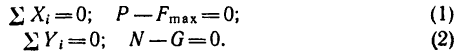
Решаем полученную систему уравнений:
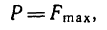
но 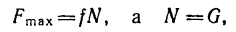
поэтому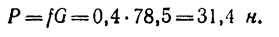
Таким образом, равновесие тела А сохраняется при условии, что к концу нити, перекинутой через блок, подвешен груз, не превышающий по весу 31,4 н.
При этом масса груза Р
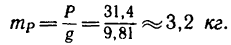
Задача №4
При каком минимальном коэффициенте трения между полом и лестницей последняя может находиться в равновесии, опираясь верхним концом о гладкую стену, как показано на рис. 120, а? Вес лестницы G = 120 н.
Решение.
1. На лестницу действует только одна нагрузка — ее собственный вес, приложенный в точке С посредине длины лестницы АВ.
2. Вес лестницы уравновешен реакцией 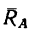 гладкой стены и реакцией шероховатого пола, которую заменим двумя составляющими:
гладкой стены и реакцией шероховатого пола, которую заменим двумя составляющими: 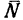 — нормальной составляющей и
— нормальной составляющей и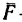 —силой трения (рис. 120,6).
—силой трения (рис. 120,6).
3. Составим три уравнения равновесия:
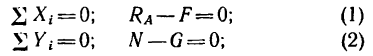
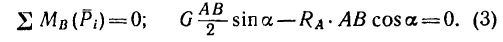
4. Из уравнений (1) и (3)
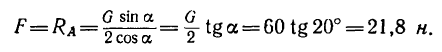
А так как N = G [из уравнения (2)[, то минимальный коэффициент трения, обеспечивающий равновесие лестницы.
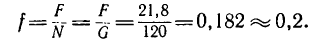
Таким образом, при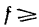 0,2 лестница находится в равновесии.
0,2 лестница находится в равновесии.
Задача №5
В месте соприкосновения пола и лестницы в предыдущей задаче коэффициент трения f= 0,4. Сможет ли человек, масса которого 70 кг, подняться по лестнице до самого верха и чтобы лестница при этом не скользила по полу?
Решение.
1. К силам 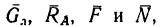 действующим на лестницу и приведенным в предыдущей задаче, необходимо добавить еще одну нагрузку —вес человека
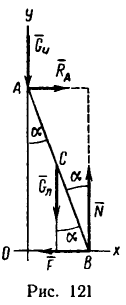
действующим на лестницу и приведенным в предыдущей задаче, необходимо добавить еще одну нагрузку —вес человека 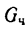 — и приложить его у верхнего конца лестницы (рис. 121).
— и приложить его у верхнего конца лестницы (рис. 121).
2. Вес человека
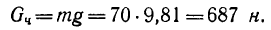
3. Человек сможет подняться до самого верха лестницы лишь в том случае, если горизонтальная составляющая реакции пола (сила 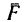 на рис. 121) будет меньше
на рис. 121) будет меньше 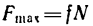 максимального значения силы трения, возможного при данном коэффициенте трения.
максимального значения силы трения, возможного при данном коэффициенте трения.
4. Составим уравнения равновесия:
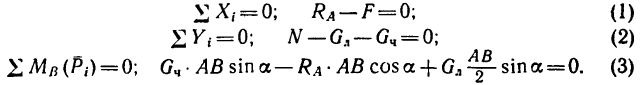
5. Из уравнения (2)
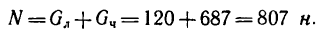
Максимальная сила трения, которая может возникнуть в данном случае
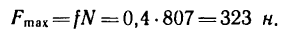
Из уравнений (1) и (3) находим силу F—горизонтальную составляющую реакции пола, которая может обеспечить равновесие лестницы с человеком, стоящим наверху:
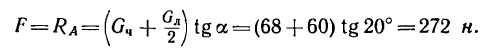
Таким образом,
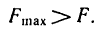
Следовательно, человек сможет подняться по лестнице до самого верха.
- Заказать решение задач по теоретической механике
Задача №6
При каких значениях угла а, образуемого с гладкой вертикальной стеной, лестница, опирающаяся нижним концом о шероховатый горизонтальный пол, будет находиться в равновесии, если, кроме собственного веса, она ничем не нагружена и известно, что коэффициент трения при соприкосновении лестницы с полом f?
Решение.
1. Для решения этой задачи воспользуемся рис. 120, б, так как на лестницу действуют те же четыре силы: вес лестницы 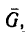 реакция гладкой стены
реакция гладкой стены 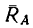 и две составляющие реакции пола —
и две составляющие реакции пола —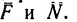
2. Лестница не выйдет из состояния равновесия (не начнет скользить) до тех пор, пока

т. е. пока горизонтальная составляющая реакции пола остается меньше максимальной силы трения, возникающей при опирании лестницы о пол в данном случае.
3. Из уравнений (1) и (3), составленных при решении задачи 90-15, найдено, что

Сопоставляем уравнения (а) и (б):
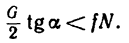
А так как в данном случае G =N, то лестница находится равновесии до тех пор, пока выполняется неравенство

или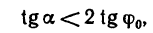
где 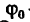 — угол трения.
— угол трения.
Следовательно, лестница находится в равновесии до тех пор, пока тангенс угла, образуемого лестницей с вертикальной гладкой стеной, остается меньше удвоенного коэффициента трения между лестницей и полом. Например, при f=0,4
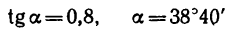
и неравенство (в) соблюдается при значениях углов
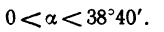
Следовательно, при f=0,4 лестница не будет скользить по полу при любом значении угла a от 0 до 38°40′.
Следующую задачу рекомендуется решить самостоятельно.
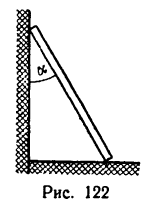
Задача №7
При каких значениях угла a однородная лестница, опирающаяся на шероховатые стену и пол (рис. 122), будет находиться в равновесии? Коэффициенты трения при опирании лестницы о стену и о пол считать одинаковыми и равными f.
Ответ. 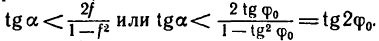
Указание. В данной задаче в системе сил, действующих на лестницу, образуется пять неизвестных: четыре реакции и угол а. Поэтому при решении задачи нужно к трем уравнениям равновесия добавить еще два уравнения, выражающих зависимость сил трения от нормального давления.
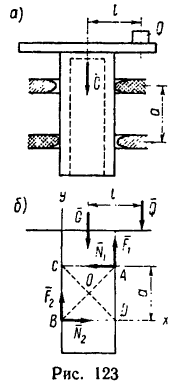
Задача №8
Цилиндр с горизонтальной площадкой наверху (рис. 123, а), находясь в двух кольцевых направляющих, скользит вниз, так как между поверхностью цилиндра и поверхностями направляющих имеется незначительный зазор. Вес цилиндра 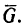 На каком наименьшем расстоянии l от оси цилиндра необходимо поместить груз Q, чтобы цилиндр перестал скользить? Коэффициент трения f. Расстояние между направляющими кольцами а.
На каком наименьшем расстоянии l от оси цилиндра необходимо поместить груз Q, чтобы цилиндр перестал скользить? Коэффициент трения f. Расстояние между направляющими кольцами а.
Решение.
1. На цилиндр в состоянии равновесия действуют две нагрузки: вес 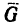 и груз
и груз 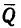 (рис. 123, б).
(рис. 123, б).
2. Груз Q, помещенный на горизонтальную площадку, прижимает цилиндр к верхнему направляющему кольцу в точке А, а к нижнему — в точке В. Благодаря зазору в точках С и D цилиндр не касается направляющих колец. В точках А и В возникают две реакции, которые заменим их составляющими 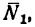
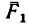 (в точке А) и
(в точке А) и 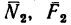 (в точке В).
(в точке В).
3. Образовалось пять неизвестных величин: 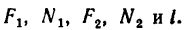
Если спроектировать все силы на ось х, то получим

откуда

Так как и

и

также, имея в виду равенство (1а), находим что

Скоректировав все силы на ось у, получим четвертое уравнение:

откуда с учетом (За)
Приняв за центр моментов точку О, лежащую на оси цилиндра и на середине расстояния а, составим пятое уравнение — уравнение моментов, в котором d- диаметр цилиндра (d = CA = BD):
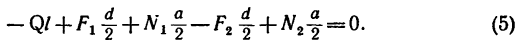
Имея в виду равенства (1а) и (За), уравнение (5) можно упростить так:
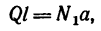
откуда

Если теперь в уравнение (2) подставить значение 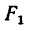 из (4а), то
из (4а), то
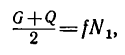
откуда
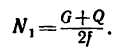
И теперь выражение (5а) принимает окончательный вид: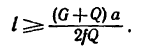
При значениях /, удовлетворяющих полученному неравенству, цилиндр не скользит вниз.
Задача №9
Тело А поставлено на негладкую пластину ВС, которую можно поворачивать около шарнира В. Коэффициент трения f между телом А и пластиной ВС известен. Определить, при каких значениях угла а (рис. 124, а) тело А будет оставаться на пластине в покое? Решение.
1. Представим, что пластина ВС наклонена к горизонту на некоторый угол а (рис. 124, б).
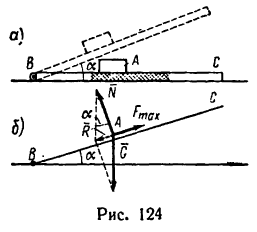
При этом положении пластины на тело А действуют три силы: его собственный вес 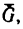 нормальная реакция
нормальная реакция 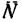 пластины и сила трения
пластины и сила трения 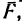 действующая на тело вдоль пластины и которая при некотором положении пластины ВС сможет достичь максимального значения.
действующая на тело вдоль пластины и которая при некотором положении пластины ВС сможет достичь максимального значения.
2. Тело А будет находиться в покое до тех пор, пока равнодействующая сил 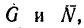 направленная вдоль пластины, будет оставаться меньше
направленная вдоль пластины, будет оставаться меньше 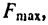 т. е. пока
т. е. пока
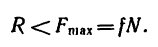
но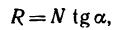
поэтому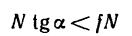
или 
Следовательно, пока тангенс угла наклона пластины к горизонту меньше коэффициента трения, тело А остается в покое.
Это положение выражает так называемое условие самоторможения тела по наклонной плоскости.
3. Учитывая, что
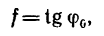
где 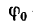 — угол трения, неравенство (а) можно представить в виде
— угол трения, неравенство (а) можно представить в виде
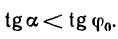
Так как углы 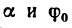 —острые и, следовательно, меньшему тан генсу соответствует меньший угол, последнее неравенство можно заменить равносильным неравенством
—острые и, следовательно, меньшему тан генсу соответствует меньший угол, последнее неравенство можно заменить равносильным неравенством
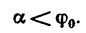
Тело А находится в покое на наклонной плоскости до тех пор, пока угол наклона плоскости меньше угла трения.
Следующую задачу рекомендуется решить самостоятельно.
Равновесие при наличии трения
Постановка Задачи. Конструкция состоит из двух шарнирно соединенных между собой тел. Одна из опор конструкции представляет собой одностороннюю связь и допускает проскальзывание с трением. Коэффициент трения, размеры конструкции и часть внешних нагрузок заданы. Найти пределы изменения одной из внешних нагрузок, действующей на конструкцию в условии равновесия.
План решения:
1. Задаем направление возможного движения подвижной опоры, скользящей с трением. Прикладываем к этой опоре силу трения, направляя ее в сторону противоположную возможному движению. Предельное значение силы трения связываем с величиной нормальной реакции опоры N по формуле Кулона 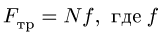 — коэффициент трения, зависящий от свойств контактирующих материалов и заданный в условии задачи.
— коэффициент трения, зависящий от свойств контактирующих материалов и заданный в условии задачи.
2. Решаем задачу о равновесии системы тел. Для этого разбиваем систему на две отдельные части, для которых составляем и решаем уравнения равновесия. Из решения определяем предельное значение нагрузки д.чя заданного направления скольжения опоры.
3. Меняем направление возможного движения системы и направление предельной силы трения. Предыдущий пункт плана выполняем заново и определяем другое предельное значение нагрузки. Два найденных значения нагрузки определяют ту область ее изменения, при которой конструкция находится в равновесии.
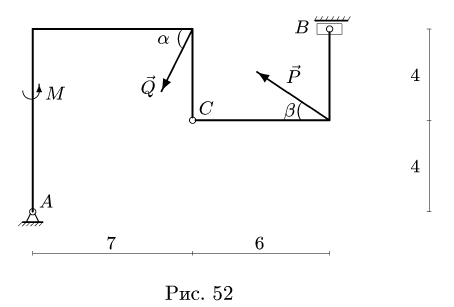
Задача №10
Конструкция состоит из двух частей, шарнирно соединенных в точке С (рис. 52). Опора В представляет собой одностороннюю связь и допускает проскальзывание с коэффициентом трения 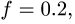 опора А — неподвижный шарнир. К конструкции приложена пара сил с моментом М = 10 кНм, сила Q = 10 кН под углом
опора А — неподвижный шарнир. К конструкции приложена пара сил с моментом М = 10 кНм, сила Q = 10 кН под углом 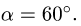
Размеры даны в метрах. Найти продолы изменения нагрузки Р, действующей под углом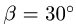 на конструкцию, в условии равновесия.
на конструкцию, в условии равновесия.
Решение
1. Задаем направление возможного движения подвижной опоры, скользящей с трением Предполагая возможное движение ползуна В влево, силу трения 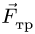 направим направо (рис. 53). Предельное значение силы трения связываем с нормальной реакцией опоры N по формуле Кулона:
направим направо (рис. 53). Предельное значение силы трения связываем с нормальной реакцией опоры N по формуле Кулона:

где 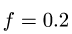 — коэффициент трения.
— коэффициент трения.
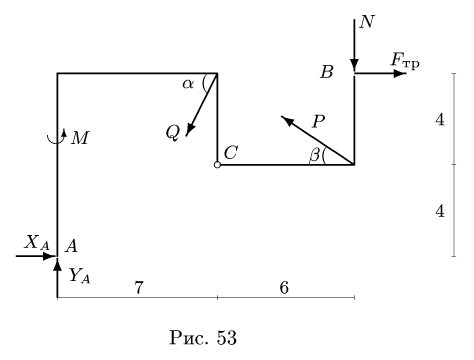
2. Решаем задачу о равновесии системы тел. Для этого систему разбиваем по шарниру С на две отдельные части — АС и СВ. Реакции шарнира С 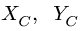 для левой и правой части направлены в противоположные стороны (рис. 54). К точке А прикладываем две составляющие реакции неподвижного шарнира
для левой и правой части направлены в противоположные стороны (рис. 54). К точке А прикладываем две составляющие реакции неподвижного шарнира 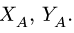
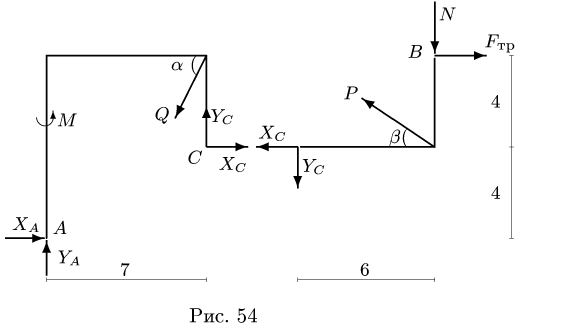
Действие ползуна заменяем нормальной реакцией N, направленной вниз, так как ползун по условию задачи является односторонней связью, и силой трения 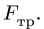 Из множества комбинаций уравнений равновесия (§ 2.4, с. 60) выберем уравнение моментов относительно точки А для всей системы в целом (рис. 53) и сумму моментов относительно С для правой части:
Из множества комбинаций уравнений равновесия (§ 2.4, с. 60) выберем уравнение моментов относительно точки А для всей системы в целом (рис. 53) и сумму моментов относительно С для правой части:
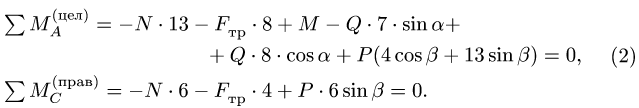
Уравнения (2) вместе с законом Кулона (1) образуют замкнутую систему трех линейных уравнений с тремя неизвестными 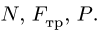 Решение системы имеет вид
Решение системы имеет вид
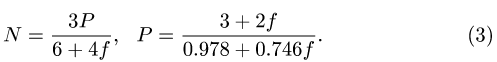
При 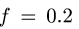 получаем
получаем 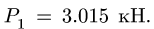 Эта нагрузка для движения влево является предельной.
Эта нагрузка для движения влево является предельной.
3. Меняем направление возможного движения системы и направление предельной силы трения. Пусть ползун В движется вправо. Силу 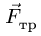 направим в противоположную сторону. Очевидно, знак момента силы
направим в противоположную сторону. Очевидно, знак момента силы 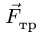 в уравнениях (2) изменится на противоположный, следовательно, решение для нового направления движения будет отличаться от (3) только знаком при
в уравнениях (2) изменится на противоположный, следовательно, решение для нового направления движения будет отличаться от (3) только знаком при 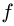 . Формально подставляя в (3)
. Формально подставляя в (3) 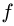 = —0.2, получим
= —0.2, получим 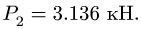 Значения
Значения 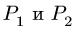 являются границами области равновесия.
являются границами области равновесия.
Чтобы убедиться, что равновесие соответствует значениям нагрузки между этими числами, определим Р при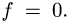 Действительно, из (3) имеем
Действительно, из (3) имеем 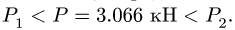
Из выражения (3) для N также следует, что при 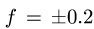 нормальная реакция N > 0, поэтому отрыв ползуна В от поверхности невозможен. Таким образом, рама находится в равновесии при
нормальная реакция N > 0, поэтому отрыв ползуна В от поверхности невозможен. Таким образом, рама находится в равновесии при
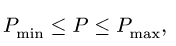
где
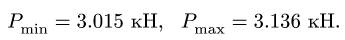
Этим нагрузкам соответствуют следующие значения нормальной реакции: 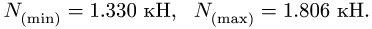
Замечание. Неравенство 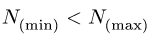 не является обязательным.
не является обязательным.
Трение качения
Постановка задачи. Система состоит из двух цилиндров, соединенных стержнем. Цилиндры могут кататься без проскальзывания, один цилиндр без сопротивления, другой — с трением качения. В каких пределах меняется внешний момент, приложенный к одному из цилиндров, в условии равновесия системы?
Трение качения происходит за счет деформации цилиндра и опорной поверхности в месте контакта. В результате реакция опоры смещается в сторону возможного движения на половину длины площадки контакта и создает момент сопротивления. Плечо этого момента принимают за коэффициент трения качения. Таким образом, 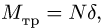 где N— реакция опоры,
где N— реакция опоры, 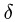 — коэффициент трения качения, имеющий размерность длины. Так в рамках теоретической механики, где изучается твердое тело, для объяснения явления трения качения вводят гипотезу деформируемости. Считают, что область деформаций
— коэффициент трения качения, имеющий размерность длины. Так в рамках теоретической механики, где изучается твердое тело, для объяснения явления трения качения вводят гипотезу деформируемости. Считают, что область деформаций
в теле мала, а глубиной продавливания цилиндра в поверхность (или величиной смятия цилиндра) пренебрегают. Коэффициент трения качения зависит не только от свойств материала цилиндра и поверхности, но и от радиуса цилиндра.
План решения:
1. Задаем направление возможного движения при достижении условия предельного равновесия. К катящемуся телу (цилиндру, колесу) прикладываем момент трения качения, направляя его в сторону, противоположную возможному движению. Не забываем про силу сцепления в точке контакта, направленную вдоль плоскости.
2. Решаем задачу о равновесии системы тел. Используем метод разбиения системы на отдельные тела. Внешние и внутренние связи заменяем их реакциями. Составляем и решаем уравнения равновесия. Оси координат для уравнения проекций для цилиндрических тел выбираем вдоль нормальной реакции, а уравнение моментов составляем относительно точки касания. Из решения системы уравнений равновесия определяем условие предельного равновесия.
3. Меняем направление возможного движения системы и направление момента трения качения. Решаем задачу заново, определяем второе условие предельного равновесия.
Задача №11
Система состоит из двух цилиндров весом 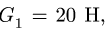 и
и 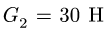 с одинаковыми радиусами R = 50 см, соединенных однородным стержнем веса
с одинаковыми радиусами R = 50 см, соединенных однородным стержнем веса 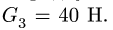 Цилиндры могут кататься без проскальзывания, цилиндр 1 — без сопротивления, а цилиндр 2 — с трением качения.
Цилиндры могут кататься без проскальзывания, цилиндр 1 — без сопротивления, а цилиндр 2 — с трением качения.
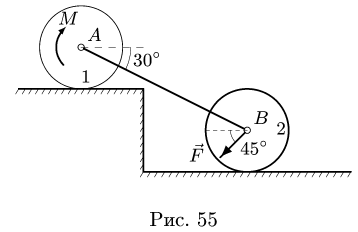
Коэффициент трения качения 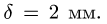 К цилиндру 1 приложена пара с моментом М. К оси цилиндра 2 приложена наклонная сила F = 10 Н (рис. 55). В каких пределах меняется момент М в условии равновесия системы?
К цилиндру 1 приложена пара с моментом М. К оси цилиндра 2 приложена наклонная сила F = 10 Н (рис. 55). В каких пределах меняется момент М в условии равновесия системы?
Решение
1. Задаем направление возможного движения при достижении условия предельного равновесия. Пусть за счет достаточно большой, по сравнению с моментом М, силы F произойдет движение системы влево. Тогда момент трения качения, приложенный к цилиндру 2, будет направлен по часовой стрелке (рис. 57). Его величину находим по формуле 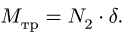
2. Решаем задачу о равновесии системы двух цилиндров и стержня. Разбиваем систему на три тела (рис. 56, 57, 58). Внешние связи заменяем реакциями 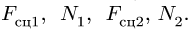
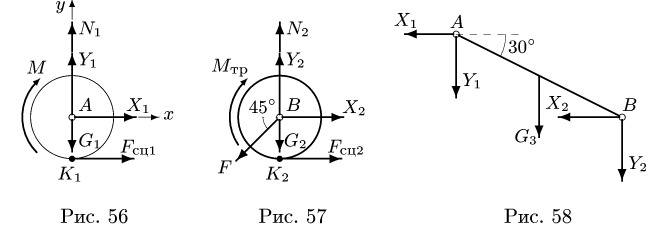
Реакции 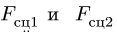 приложены к цилиндрам в точках их касания поверхностей, вызваны силами сцепления (трения) и обеспечивают вращение цилиндров. Реакции внутренних связей —
приложены к цилиндрам в точках их касания поверхностей, вызваны силами сцепления (трения) и обеспечивают вращение цилиндров. Реакции внутренних связей — 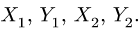
При составлении системы семи уравнений с неизвестными 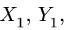
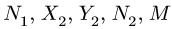 избегаем уравнения, в которые входят неизвестные реакции
избегаем уравнения, в которые входят неизвестные реакции 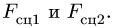
Составляем уравнения равновесия для цилиндра 1 (рис. 56):
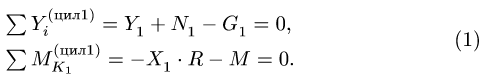
Уравнения равновесия цилиндра 2 (рис. 57) имеют вид
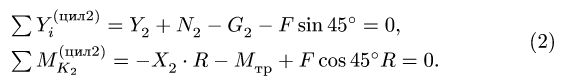
3.2.Трения качения
Уравнения равновесия стержня АВ (рис. 58) имеют вид
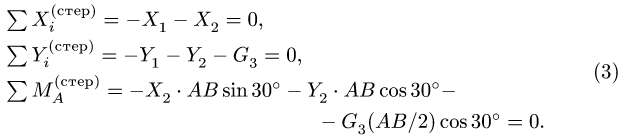
Из решения системы уравнений (1-3) определяем
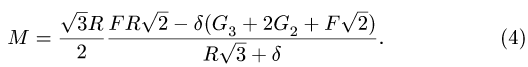
Радиус и коэффициент трения качения переводим в метры R = 0.5 м, 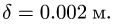 Получаем М — 3.414 Нм. Вычисляем нормальные реакции опор:
Получаем М — 3.414 Нм. Вычисляем нормальные реакции опор:
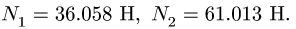
Убеждаемся, что 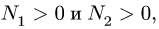 что соответствует наличию опоры. Если реакция опоры равна нулю, то это означает отрыв тела от поверхности, отрицательной реакции опоры
что соответствует наличию опоры. Если реакция опоры равна нулю, то это означает отрыв тела от поверхности, отрицательной реакции опоры 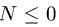 в задаче с односторонней связью не существует (физически не реализуется).
в задаче с односторонней связью не существует (физически не реализуется).
3. Меняем направление возможного движения системы. Пусть за счет действия момента М произойдет движение системы вправо. Момент трения качения направим против часовой стрелки (рис. 59). Составляя уравнения равновесия для новой системы сил, заметим, что отличие от прежней системы проявляется только в знаке 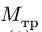 во втором уравнении равновесия (2). Так как
во втором уравнении равновесия (2). Так как 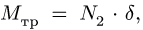 то новое решение для М будет формально отличаться от (4) только знаком у коэффициента трения
то новое решение для М будет формально отличаться от (4) только знаком у коэффициента трения 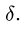 Поэтому, не решая (и даже не составляя) системы уравнений равновесия типа (1-3) для нового направления возможного движения, записываем ответ, изменяя знаки у
Поэтому, не решая (и даже не составляя) системы уравнений равновесия типа (1-3) для нового направления возможного движения, записываем ответ, изменяя знаки у 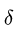 в (4):
в (4):
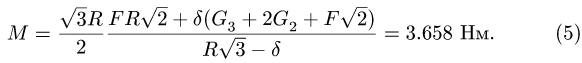
Точно так же находим нормальные реакции опор: 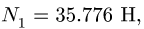
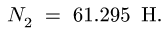 При равновесии системы момент, приложенный к
При равновесии системы момент, приложенный к
цилиндру 1, изменяется в пределах (в Нм) 
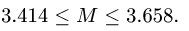
- Пространственная система сил
- Центр тяжести
- Кинематика точки
- Плоское движение твердого тела
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
Тре́ние — физическое явление
соприкасающихся тел при их относительном смещении в плоскости касания (внешнее трение) либо при относительном смещении параллельных слоёв жидкости, газа или деформируемого твёрдого тела (внутреннее трение, или вязкость). Далее в этой статье под трением понимается лишь внешнее трение. Изучением процессов трения занимается раздел физики, который называется механикой фрикционного взаимодействия, или трибологией.
Трение главным образом имеет электронную природу при условии, что вещество находится в нормальном состоянии. В сверхпроводящем состоянии вдалеке от критической температуры основным «источником» трения являются фононы, а коэффициент трения может уменьшиться в несколько раз[ссылка 1].
Сила трения[править | править код]
Сила трения — это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению. Причиной возникновения трения является шероховатость трущихся поверхностей и взаимодействие молекул этих поверхностей. Сила трения зависит от материала трущихся поверхностей и от того, насколько сильно эти поверхности прижаты друг к другу. В простейших моделях трения (закон Кулона для трения) считается, что сила трения прямо пропорциональна силе нормальной реакции между трущимися поверхностями. В целом же, в связи со сложностью физико-химических процессов, протекающих в зоне взаимодействия трущихся тел, процессы трения принципиально не поддаются описанию с помощью простых моделей классической механики.
Разновидности силы трения[править | править код]
При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на:
- Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения.
- Трение качения — момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого.
- Трение покоя — сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения.
- Трение кручения — момент силы, возникающий между двумя контактирующими телами при вращении одного из них относительно другого и направленный против вращения. Определяется формулой:
, где
— нормальное давление,
— коэффициент трения кручения, имеющий размерность длины[1].
Характер фрикционного взаимодействия[править | править код]
В физике взаимодействие трения принято разделять на:
- сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками (в том числе и твёрдыми смазочными материалами) — очень редко встречающийся на практике случай, характерная отличительная черта сухого трения — наличие значительной силы трения покоя;
- граничное, когда в области контакта могут содержаться слои и участки различной природы (оксидные плёнки, жидкость и так далее) — наиболее распространённый случай при трении скольжения;
- смешанное, когда область контакта содержит участки сухого и жидкостного трения;
- жидкостное (вязкое), при взаимодействии тел, разделённых слоем твёрдого тела (порошком графита), жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость, величина вязкого трения характеризуется вязкостью среды;
- эластогидродинамическое (вязкоупругое), когда решающее значение имеет внутреннее трение в смазывающем материале, возникает при увеличении относительных скоростей перемещения.
Сила реакции опоры[править | править код]

Сила нормальной реакции определяется как результирующая сила, сжимающая две параллельные поверхности вместе, а её направление перпендикулярно этим поверхностям. В простом случае, когда масса лежит на горизонтальной поверхности, единственной составляющей нормальной силы является сила тяжести, где 



Коэффициент трения — это эмпирическое (экспериментально измеренное) структурное свойство, которое зависит только от различных аспектов контактирующих материалов, таких как шероховатость поверхности. Коэффициент трения не зависит от массы или объёма. Например, большой алюминиевый блок имеет тот же коэффициент трения, что и маленький алюминиевый блок. Однако величина самой силы трения зависит от силы реакции опоры и, следовательно, от массы блока.
В зависимости от ситуации расчёт нормальной силы 








Если объект находится на наклонной поверхности, например на наклонной плоскости, нормальная (к поверхности) сила тяжести меньше, чем 
В общем, процесс решения любой статической задачи с трением состоит в том, чтобы рассматривать соприкасающиеся поверхности предварительно как неподвижные, чтобы можно было рассчитать соответствующую тангенциальную силу реакции между ними. Если эта сила реакции удовлетворяет 

Коэффициент трения[править | править код]
Коэффициент трения, часто обозначаемый греческой буквой µ, представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения. Коэффициент трения зависит от используемых материалов; например, лёд имеет низкий коэффициент трения о сталь, а резина — высокий коэффициент трения при скольжении по дорожному покрытию. Коэффициенты трения находятся в диапазоне от почти нуля до значений больше единицы. Трение между металлическими поверхностями больше между двумя поверхностями из одинаковых металлов, чем между двумя поверхностями из разных металлов — следовательно, латунь будет иметь более высокий коэффициент трения при движении по латуни, но меньше при движении по стали или алюминию[2].
Для поверхностей в состоянии покоя относительно друг друга 

Для поверхностей, находящихся в относительном движении 


Артур Морин ввёл этот термин и продемонстрировал полезность коэффициента трения[4]. Коэффициент трения — это эмпирическая величина — его нужно измерить экспериментально и он не может быть определён путём расчётов[5]. Более грубые поверхности обычно имеют более высокие эффективные значения коэффициента трения. Как статические, так и кинетические коэффициенты трения зависят от пары контактирующих поверхностей; для данной пары поверхностей коэффициент трения покоя обычно больше, чем коэффициент кинетического трения; в некоторых наборах два коэффициента равны, например, тефлон на тефлоне.
Большинство сухих материалов имеют значения коэффициента трения от 0,3 до 0,6. Значения вне этого диапазона встречаются реже, но тефлон, например, может иметь коэффициент всего 0,04. Нулевое значение означало бы отсутствие трения, ненаблюдаемое свойство. Резина при контакте с другими поверхностями может иметь коэффициент трения от 1 до 2. Иногда утверждают, что μ всегда <1, но это неверно. В то время как в большинстве соответствующих приложений μ <1, значение выше 1 просто означает, что сила, необходимая для скольжения объекта по поверхности, больше, чем нормальное усилие поверхности на объект. Например, поверхности, покрытые силиконовым каучуком или акриловым каучуком, имеют коэффициент трения, который может быть значительно больше 1.
Хотя часто утверждается, что коэффициент трения является «материальным свойством», его лучше классифицировать как «системное свойство». В отличие от истинных свойств материала (таких как проводимость, диэлектрическая проницаемость, предел текучести), коэффициент трения для любых двух материалов зависит от системных переменных, таких как температура, скорость, атмосфера, а также от того, что сейчас обычно называют временем старения и разрушения; а также от геометрических свойств границы раздела материалов, а именно структуры их поверхностей[3]. Например, медный штифт, скользящий по толстой медной пластине, может иметь коэффициент трения, который изменяется от 0,6 при низких скоростях (скольжение металла по металлу) до менее 0,2 при высоких скоростях, когда поверхность меди начинает плавиться из-за нагрева от трения. Последняя скорость, конечно, не определяет коэффициента трения однозначно; если диаметр штифта увеличивается так, что нагрев от трения быстро устраняется, температура падает, и штифт остаётся твердым, а коэффициент трения повышается до значения, наблюдаемого при испытании на «низкой скорости».
При определённых условиях некоторые материалы имеют очень низкие коэффициенты трения. Примером является (высокоупорядоченный пиролитический) графит, который может иметь коэффициент трения ниже 0,01[6]. Этот режим сверхнизкого трения называется сверхсмазкой.
Статическое трение[править | править код]
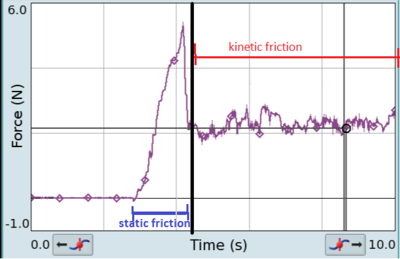
Когда масса неподвижна, то объект испытывает статическое трение. Трение увеличивается по мере увеличения приложенной силы, пока блок не переместится. После того, как блок начнёт перемещение, он испытывает кинетическое трение, которое меньше максимального статического трения.
Статическое трение — это трение между двумя или более твёрдыми объектами, которые не движутся относительно друг друга. Например, статическое трение может предотвратить скольжение объекта по наклонной поверхности. Коэффициент статического трения, обычно обозначаемый как μs, обычно выше, чем коэффициент кинетического трения. Считается, что статическое трение возникает в результате особенностей шероховатости поверхности на различных масштабах длины на твёрдых поверхностях. Эти особенности, известные как неровности, присутствуют вплоть до наноразмеров и приводят к тому, что настоящий контакт твёрдого тела с твёрдым телом существует только в ограниченном количестве точек, составляющих лишь часть видимой или номинальной площади контакта[7]. Линейность между приложенной нагрузкой и истинной площадью контакта, возникающая из-за деформации неровностей, приводит к линейности между статической силой трения и нормальной силой, обнаруживаемой для типичного трения Амонтона — Кулона[8].
Сила статического трения должна быть преодолена приложенной силой, прежде чем объект сможет двигаться. Максимально возможная сила трения между двумя поверхностями до начала скольжения является произведением коэффициента трения покоя и нормальной силы: 



Примером статического трения может служить сила, препятствующая скольжению автомобильного колеса при качении по земле. Несмотря на то, что колесо находится в движении, участок шины, контактирующий с землёй, неподвижен относительно земли, поэтому это статическое, а не кинетическое трение.
Максимальное значение статического трения иногда называют ограничивающим трением[10], хотя этот термин не используется повсеместно[11].
Кинетическое трение[править | править код]
Кинетическое трение, также известное как трение скольжения, возникает, когда два объекта движутся относительно друг друга и трутся друг о друга (как салазки по земле). Коэффициент кинетического трения обычно обозначается как μk и обычно меньше коэффициента трения покоя для тех же материалов[12][13]. Однако Ричард Фейнман отмечает, что «с сухими металлами очень трудно показать какое-либо различие»[14]. Сила трения между двумя поверхностями после начала скольжения является произведением коэффициента кинетического трения и силы реакции опоры: 
Новые модели показывают, насколько кинетическое трение может быть больше, чем трение покоя. Кинетическое трение, во многих случаях, в первую очередь вызвано химической связью между поверхностями, а не переплетёнными неровностями[16]; однако во многих других случаях эффекты шероховатости являются доминирующими, например, при трении резины о дорогу. Шероховатость поверхности и площадь контакта влияют на кинетическое трение для микро- и наноразмерных объектов, где силы рапределённые по площади поверхности преобладают над силами инерции[17].
Происхождение кинетического трения в наномасштабе можно объяснить термодинамикой[18]. При скольжении новая поверхность образуется в задней части скользящего истинного контакта, а существующая поверхность исчезает в передней части. Поскольку все поверхности включают в себя термодинамическую поверхностную энергию, работа должна быть затрачена на создание новой поверхности, а энергия выделяется в виде тепла при удалении поверхности. Таким образом, требуется сила, чтобы переместить заднюю часть контакта, и тепло трения выделяется спереди.

Угол трения θ, когда блок только начинает скользить.
Угол трения[править | править код]
Для некоторых приложений более полезно определять статическое трение в терминах максимального угла, перед которым один из элементов начнёт скользить. Он называется углом трения и определяется как:
где θ — угол от горизонтали, а μs — статический коэффициент трения между телами[19]. Эту формулу также можно использовать для расчета μs на основе эмпирических измерений угла трения.
Трение на атомном уровне[править | править код]
Определение сил, необходимых для перемещения атомов друг мимо друга, является сложной задачей при разработке наномашин. В 2008 году учёные впервые смогли переместить отдельный атом по поверхности и измерить необходимые силы. Используя сверхвысокий вакуум и почти низкую температуру (5 К), при помощи модифицированного атомно-силового микроскопа перемещались атомы кобальта и молекулы монооксида углерода по поверхности меди и платины[20].
Закон Амонтона — Кулона[править | править код]
Основной характеристикой трения является коэффициент трения 
В простейших случаях сила трения 

| Пары материалов |  покоя покоя |
 скольжения скольжения
|
|---|---|---|
| Сталь-Сталь | 0,5—0,8[21] | 0,15—0,18 |
| Резина-Сухой асфальт | 0,95—1 | 0,5—0,8 |
| Резина-Влажный асфальт | 0,25—0,75 | |
| Лёд-Лёд | 0,05—0,1 | 0,028 |
| Резина-Лёд | 0,3 | 0,15—0,25 |
| Стекло-Стекло | 0,9 | 0,7 |
| Нейлон-Нейлон | 0,15—0,25 | |
| Полистирол-Полистирол | 0,5 | |
| Плексиглас, оргстекло | 0,8 |
Закон Амонтона — Кулона с учётом адгезии[править | править код]
Для большинства пар материалов значение коэффициента трения 


Прикладное значение[править | править код]
Трение в механизмах и машинах[править | править код]
В большинстве традиционных механизмов (ДВС, автомобили, зубчатые шестерни и пр.) трение играет отрицательную роль, уменьшая КПД механизма. Для уменьшения силы трения используются различные натуральные и синтетические масла и смазки. В современных механизмах для этой цели используется также напыление покрытий (тонких плёнок) на детали. С миниатюризацией механизмов и созданием микроэлектромеханических систем (МЭМС) и наноэлектромеханических систем (НЭМС) величина трения по сравнению с действующими в механизме силами увеличивается и становится весьма значительной 
Сцепление с поверхностью[править | править код]
Наличие трения обеспечивает возможность перемещаться по поверхности. Так, при ходьбе именно за счёт трения происходит сцепление подошвы с полом, в результате чего происходит отталкивание от пола и движение вперёд. Точно так же обеспечивается сцепление колёс автомобиля (мотоцикла) с поверхностью дороги. В частности, для улучшения этого сцепления разрабатываются новые формы и специальные типы резины для покрышек, а на гоночные болиды устанавливаются антикрылья, сильнее прижимающие машину к трассе.
Трение внутри материалов[править | править код]
История[править | править код]
Греки, в том числе Аристотель, Витрувий и Плиний Старший интересовались причиной и снижением трения[22]. Они знали о различиях между статическим и кинетическим трением, а Фемистий утверждал в 350 году, что «легче продолжать движение движущегося тела, чем перемещать тело в состоянии покоя»[22][23][24][25].
Классические законы трения скольжения были открыты Леонардо да Винчи в 1493 году, который был пионером в области трибологии, но законы, задокументированные в его записных книжках, не были опубликованы и остались неизвестными[4][26][27][28][29][30]. Эти законы были переоткрыты Гийомом Амонтоном в 1699 году[31] и стали известны как три закона Амонтона сухого трения. Амонтон представлял природу трения с точки зрения неровностей поверхности и силы, необходимой для увеличения веса, прижимающего поверхности друг к другу. Эта точка зрения была развита Бернаром Форестом де Белидором[32] и Леонардом Эйлером в 1750 году, которые вывели угол естественного откоса груза на наклонной плоскости и впервые различили статическое и кинетическое трение[33]. Иоанн Теофил Дезагюлье в 1734 году первым осознал роль адгезии в трении[34]. Эти микроскопические силы заставляют поверхности слипаться; и он предположил, что трение — это сила, необходимая для разрыва прилегающих поверхностей.
Понимание трения в дальнейшем развил Шарль-Огюстен де Кулон (1785)[31]. Кулон исследовал влияние четырёх основных факторов, влияющих на трение: природы контактирующих материалов и покрытия их поверхностей; протяженность площади поверхности; нормальное давление (или нагрузка); и продолжительность контакта поверхностей (время покоя)[4]. Кулон также рассмотрел влияние скорости скольжения, температуры и влажности, чтобы выбрать между различными икорктическими объяснениями природы трения. Различие между статическим и кинетическим трением появляется в законе трения Кулона, хотя это различие уже было замечено Иоганном Андреасом фон Зегнером в 1758 году[4]. Эффект времени покоя объяснил Питер ван Мушенбрук в 1762 году путём рассмотрения поверхностей волокнистых материалов со сцепляющимися вместе волокнами, что занимает конечное время, в течение которого увеличивается трение.
Джон Лесли (1766—1832) отметил слабость взглядов Амонтона и Кулона: если трение возникает из-за того, что груз поднимается по наклонной плоскости последовательных выступов, то почему тогда оно не уравновешивается движением вниз по противоположному склону? Лесли столь же скептически относился к роли адгезии, предложенной Дезагюлье, которая в целом должна приводить как к ускорению, так и к замедлению движения[4]. По мнению Лесли, трение следует рассматривать как зависящий от времени процесс уплощения, сдавливания неровностей, что создаёт новые препятствия в тех люластях, что раньше было полостями.
Артур-Жюль Морен (1833) разработал концепцию трения скольжения по сравнению с трением качения. Осборн Рейнольдс (1866) вывел уравнение вязкого течения. Это завершило классическую эмпирическую модель трения (статического, кинетического и жидкостного), обычно используемую сегодня в технике[26]. В 1877 году Флеминг Дженкин и Джеймс А. Юинг исследовали непрерывность статического и кинетического трения[35].
В центре внимания исследований в 20 веке стало понимание физических механизмов трения. Франк Филип Боуден и Дэвид Табор (1950) показали, что на микроскопическом уровне фактическая площадь контакта между поверхностями составляет очень небольшую часть видимой площади[27]. Эта фактическая площадь контакта, вызванная неровностями, увеличивается по мере увеличения давлением. Развитие атомно-силового микроскопа (1986) позволило учёным изучить трение в атомном масштабе[26] показав, что на этом масштабе сухое трение — это продукт межповерхностного сдвигового напряжения и площади контакта. Эти два открытия объясняют первый закон Амонтона; макроскопическая пропорциональность между нормальной силой и статической силой трения между сухими поверхностями.
Журналы[править | править код]
- Трение, Износ, Смазка, журнал о трении.
- Трение и Износ, журнал о трении издаётся Национальной Академией Наук Беларуси с 1980 г.
- Journal of Tribology Архивная копия от 16 января 2013 на Wayback Machine, международный журнал о трении.
- Wear, международный журнал о трении и износе.
- Таблицы коэффициентов трения, численные значения коэффициентов трения.
Литература[править | править код]
- Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 1. Трение в машинах. Теория, расчет и конструкция подшипников и подпятников скольжения. Машгиз. М.-Л. — 1947. 256 с.
- Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 2. Износ материалов. Классификация видов износа, методов и машин для лабораторного испытания материалов на износ машины и производственные на них исследования. Машгиз. М.-Л. — 1947. 220 с.
- Зайцев А. К. Основы учения о трении, износе и смазке машин. Часть 3. Износ машин. Износ машин и деталей и способы борьбы с их износом. Машгиз. М.-Л. — 1947. 164 с.
- Зайцев А. К., А. Кононов Максимович Основы учения о трении, износе и смазке машин. Часть 4. Смазка машин. Машгиз. М.-Л. — 1948. 279 с.
- Archbutt L., Deeley R.M. Lubrication and Lubicants. London. — 1927
- Арчбютт Л., Дилей Р. М. Трение, смазка и смазочные материалы. Руководство по теории и практике смазки и по методам испытания смазочных материалов. Госгоргеолнефтиздат. — Л. — 1934. — 703 с.
- 2-е изд., перераб. и доп. — М.-Л.: Гостоптехиздат. — 1940. — 824 с.
- Дерягин Б. В. Что такое трение? М.: Изд. АН СССР, 1963.
- Основы теории систем с трением/ А. П. Иванов. — М.-Ижевск: НИЦ «РХД», ИКИ, 2011. 304 с. (Предисловие автора, обнарод. в качестве анонса к книге // Нелинейная динамика, 2010. Т 6, № 4. С. 913—916).
- Крагельский И. В., Щедров В. С. Развитие науки о трении. Сухое трение. М.: Изд. АН СССР, 1956.
- Фролов, К. В. (ред.) Современная трибология: Итоги и перспективы. ЛКИ, 2008.
- Bowden F. P., Tabor D. The Friction and Lubrication of Solids. Oxford University Press, 2001.
- Persson Bo N. J.: Sliding Friction. Physical Principles and Applications. Springer, 2002.
- Popov V. L. Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation, Springer, 2009.
- Rabinowicz E. Friction and Wear of Materials. Wiley-Interscience, 1995.
Примечания[править | править код]
- На русском
- ↑ Ерин Ю. Сверхпроводимость уменьшает силу трения. Элементы.ру (15 февраля 2011). Дата обращения: 26 февраля 2011. Архивировано 22 августа 2011 года.
- На других языках
- ↑ Зиновьев В. А. Краткий технический справочник. Том 1. — М.: Государственное издательство технико-теоретической литературы, 1949. — С. 296
- ↑ Air Brake Association. The Principles and Design of Foundation Brake Rigging. — Air brake association, 1921. — P. 5. Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ 1 2 Hanaor, D. (2016). “Static friction at fractal interfaces”. Tribology International. 93: 229—238. arXiv:2106.01473. DOI:10.1016/j.triboint.2015.09.016.
- ↑ 1 2 3 4 5 Dowson, Duncan. History of Tribology. — 2nd. — Professional Engineering Publishing, 1997. — ISBN 978-1-86058-070-3.
- ↑ Valentin L. Popov (17 Jan 2014). “Generalized law of friction between elastomers and differently shaped rough bodies”. Sci. Rep. 4. DOI:10.1038/srep03750. PMID 24435002.
- ↑ Dienwiebel, Martin (2004). “Superlubricity of Graphite” (PDF). Phys. Rev. Lett. 92 (12). Bibcode:2004PhRvL..92l6101D. DOI:10.1103/PhysRevLett.92.126101. PMID 15089689. Архивировано (PDF) из оригинала 2011-09-17. Дата обращения 2021-09-18.
- ↑ multi-scale origins of static friction Архивная копия от 18 сентября 2021 на Wayback Machine 2016
- ↑ Greenwood J.A. and JB Williamson (1966). “Contact of nominally flat surfaces”. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 295 (1442).
- ↑ Nakano, K. (2020-12-10). “Dynamic stiction without static friction: The role of friction vector rotation”. Physical Review E. 102 (6): 063001. DOI:10.1103/PhysRevE.102.063001.
- ↑ Bhavikatti, S. S. Engineering Mechanics / S. S. Bhavikatti, K. G. Rajashekarappa. — New Age International, 1994. — P. 112. — ISBN 978-81-224-0617-7. Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ Beer, Ferdinand P. Vector Mechanics for Engineers / Ferdinand P. Beer, Johnston. — McGraw-Hill, 1996. — P. 397. — ISBN 978-0-07-297688-5.
- ↑ Sheppard, Sheri. Statics: Analysis and Design of Systems in Equilibrium / Sheppard, Sheri, Tongue, Benson H., Anagnos, Thalia. — Wiley and Sons, 2005. — ISBN 978-0-471-37299-8.
- ↑
Meriam, James L. Engineering Mechanics: Statics / Meriam, James L., Kraige, L. Glenn, Palm, William John. — Wiley and Sons, 2002. — ISBN 978-0-471-40646-4. - ↑ Feynman, Richard P. The Feynman Lectures on Physics, Vol. I, p. 12–5. Addison-Wesley. Дата обращения: 16 октября 2009. Архивировано 10 марта 2021 года.
- ↑ Beatty. Recurring science misconceptions in K-6 textbooks. Дата обращения: 8 июня 2007. Архивировано 7 июня 2011 года.
- ↑ Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ Makkonen, L (2012). “A thermodynamic model of sliding friction”. AIP Advances. 2 (1). Bibcode:2012AIPA….2a2179M. DOI:10.1063/1.3699027.
- ↑ Nichols, Edward Leamington. The Elements of Physics / Edward Leamington Nichols, William Suddards Franklin. — Macmillan, 1898. — Vol. 1. — P. 101. Архивная копия от 1 августа 2020 на Wayback Machine
- ↑ Ternes, Markus (2008-02-22). “The Force Needed to Move an Atom on a Surface” (PDF). Science. 319 (5866): 1066—1069. Bibcode:2008Sci…319.1066T. DOI:10.1126/science.1150288. PMID 18292336. Архивировано (PDF) из оригинала 2021-08-17. Дата обращения 2021-09-18.
- ↑ Friction theory and coefficients of friction for some common materials and materials combinations. Дата обращения: 1 января 2015. Архивировано 3 декабря 2013 года.
- ↑ 1 2 Chatterjee, Sudipta (2008). Tribological Properties of Pseudo-elastic Nickel-titanium (Thesis). University of California. pp. 11—12. ISBN 9780549844372 – via ProQuest.
Classical Greek philosophers like Aristotle, Pliny the Elder and Vitruvius wrote about the existence of friction, the effect of lubricants and the advantages of metal bearings around 350 B.C.
- ↑ Fishbane, Paul M. Physics for Scientists and Engineers / Paul M. Fishbane, Stephen Gasiorowicz, Stephen T. Thornton. — Extended. — Englewood Cliffs, New Jersey : Prentice Hall, 1993. — Vol. I. — P. 135. — «Themistius first stated around 350 B.C. that kinetic friction is weaker than the maximum value of static friction.». — ISBN 978-0-13-663246-7.
- ↑ Hecht, Eugene. Physics: Algebra/Trig. — 3rd. — Cengage Learning, 2003. — ISBN 9780534377298.
- ↑ Sambursky, Samuel. The Physical World of Late Antiquity. — Princeton University Press. — ISBN 9781400858989.
- ↑ 1 2 3 Armstrong-Hélouvry, Brian. Control of machines with friction. — USA : Springer, 1991. — P. 10. — ISBN 978-0-7923-9133-3. Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ 1 2 van Beek. History of Science Friction. tribology-abc.com. Дата обращения: 24 марта 2011. Архивировано 7 августа 2011 года.
- ↑ Hutchings, Ian M. (2016). “Leonardo da Vinci’s studies of friction” (PDF). Wear. 360–361: 51—66. DOI:10.1016/j.wear.2016.04.019. Архивировано (PDF) из оригинала 2021-08-31. Дата обращения 2021-09-18.
- ↑ Hutchings, Ian M. (2016-08-15). “Leonardo da Vinci’s studies of friction”. Wear. 360–361: 51—66. DOI:10.1016/j.wear.2016.04.019. Архивировано из оригинала 2021-09-18. Дата обращения 2021-09-18.
- ↑ Kirk. Study reveals Leonardo da Vinci’s ‘irrelevant’ scribbles mark the spot where he first recorded the laws of friction. phys.org (22 июля 2016). Дата обращения: 26 июля 2016. Архивировано 25 июля 2016 года.
- ↑ 1 2 Popova, Elena (2015-06-01). “The research works of Coulomb and Amontons and generalized laws of friction”. Friction [англ.]. 3 (2): 183—190. DOI:10.1007/s40544-015-0074-6.
- ↑ Forest de Bélidor, Bernard. «Richtige Grund-Sätze der Friction-Berechnung Архивная копия от 27 апреля 2021 на Wayback Machine» («Correct Basics of Friction Calculation»), 1737, (in German)
- ↑ Leonhard Euler. Friction Module. Nano World. Дата обращения: 25 марта 2011. Архивировано из оригинала 7 мая 2011 года.
- ↑ Goedecke, Andreas. Transient Effects in Friction: Fractal Asperity Creep. — Springer Science and Business Media, 2014. — P. 3. — ISBN 978-3709115060. Архивная копия от 18 сентября 2021 на Wayback Machine
- ↑ Fleeming Jenkin & James Alfred Ewing (1877) «On Friction between Surfaces moving at Low Speeds Архивная копия от 18 сентября 2021 на Wayback Machine», Philosophical Magazine Series 5, volume 4, pp 308-10; link from Biodiversity Heritage Library
Реакция
реальной (шероховатой) связи будет
слагаться из двух составляющих: из
нормальной реакции ![]() и
и
перпендикулярной к ней силы трения ![]() .
.
Следовательно, полная реакция ![]() будет
будет
отклонена от нормали к поверхности на
некоторый угол. При изменении силы
трения от нуля до Fпр сила R будет
меняться от N до Rпр,
а ее угол с нормалью будет расти от нуля
до некоторого предельного
значения ![]() (рис.
(рис.
26).
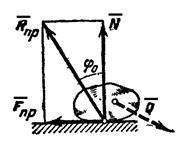
Рис.26
Наибольший
угол ![]() ,
,
который полная реакция шероховатой
связи образует с нормалью к поверхности,
называется углом
трения. Из чертежа
видно, что
![]() .
.
Так
как ![]() ,
,
отсюда находим следующую связь между
углом трения и коэффициентом трения:
![]()
При
равновесии полная реакция R,
в зависимости от сдвигающих сил, может
проходить где угодно внутри угла трения.
Когда равновесие становится предельным,
реакция будет отклонена от нормали на
угол ![]() .
.
Конусом
трения называют
конус, описанный предельной силой
реакции шероховатой связи ![]() вокруг
вокруг
направления нормальной реакции.
Если
к телу, лежащему на шероховатой
поверхности, приложить силу Р,
образующую угол ![]() с
с
нормалью (рис. 27), то тело сдвинется
только тогда, когда сдвигающее
усилие Psin![]() будет
будет
больше ![]() (мы
(мы
считаем N=Pcos![]() ,
,
пренебрегая весом тела). Но неравенство ![]() ,
,
в котором ![]() ,
,
выполняется только при ![]() ,
,
т.е. при ![]() .
.
Следовательно, никакой силой,
образующей с нормалью угол ![]() ,
,
меньший угла трения ![]() ,
,
тело вдоль данной поверхности сдвинуть
нельзя. Этим объясняются известные
явления заклинивания или самоторможения
тел.
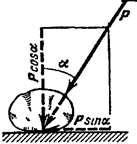
Рис.27
Для равновесия
твёрдого тела на шероховатой поверхности
необходимо и достаточно, чтобы линия
действия равнодействующей активных
сил, действующих на твёрдое тело,
проходила внутри конуса трения или по
его образующей через его вершину.
Тело нельзя вывести
из равновесия любой по модулю активной
силой, если её линия действия проходит
внутри конуса трения.
23, Трение качения
происхождение
трения качения можно наглядно представить
себе так. Когда шар или цилиндр катится
по поверхности другого тела, он немного
вдавливается в поверхность этого тела,
а сам немного сжимается. Таким образом,
катящееся тело всё время как бы вкатывается
на горку.
Рис.33
Вместе с тем
происходит отрыв участков одной
поверхности от другой, а силы сцепления,
действующие между этими поверхностями,
препятствуют этому. Оба эти явления и
вызывают силы трения качения. Чем твёрже
поверхности, тем меньше вдавливание и
тем меньше трение качения.
Трением
качения называется
сопротивление, возникающее при качении
одного тела по поверхности другого.
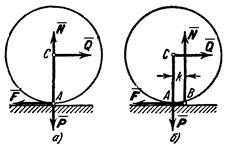
Рис.34
Рассмотрим
круглый цилиндрический каток радиуса R и
веса ![]() ,
,
лежащий на горизонтальной шероховатой
плоскости. Приложим к оси катка
силу ![]() (рис.
(рис.
34, а), меньшую Fпр.
Тогда в точке А возникает
сила трения ![]() ,
,
численно равная Q,
которая будет препятствовать скольжению
цилиндра по плоскости. Если считать
нормальную реакцию ![]() тоже
тоже
приложенной в точке А,
то она уравновесит силу ![]() ,
,
а силы ![]() и
и ![]() образуют
образуют
пару, вызывающую качение цилиндра. При
такой схеме качение должно начаться,
как видим, под действием любой, сколь
угодно малой
силы ![]() .
.
Истинная
же картина, как показывает опыт,
выглядит иначе. Объясняется это тем,
что фактически, вследствие деформаций
тел, касание их происходит вдоль некоторой
площадки АВ (рис.
34, б). При действии силы ![]() интенсивность
интенсивность
давлений у края А убывает,
а у края В возрастает.
В результате реакция ![]() оказывается
оказывается
смещенной в сторону действия силы ![]() .
.
С увеличением ![]() это
это
смещение растет до некоторой предельной
величины k.
Таким образом, в предельном положении
на каток будут действовать пара (![]() ,
, ![]() )
)
с моментом ![]() и
и
уравновешивающая ее пара (![]() )
)
с моментом Nk.
Из равенства моментов находим ![]() или
или
![]()
Пока ![]() ,
,
каток находится в покое; при ![]() начинается
начинается
качение.
Входящая
в формулу линейная
величина k называется коэффициентом
трения качения. Измеряют
величину k обычно
в сантиметрах. Значение
коэффициента k зависит
от материала тел и определяется
опытным путем.
Коэффициент трения
качения при качении в первом приближении
можно считать не зависящим от угловой
скорости качения катка и его скорости
скольжения по плоскости.
Для
вагонного колеса по рельсу k=0,5
мм.
Рассмотрим
движение ведомого колеса. ![]()
Качение
колеса начнется, когда выполнится
условие QR>M или Q>Mmax/R=kN/R
Скольжение
колеса начнется, когда выполнится
условие Q>Fmax=fN.
Обычно
отношение ![]() и
и
качение начинается раньше скольжения.
Если ![]() , то колесо
, то колесо
будет скользить по поверхности, без
качения.
Отношение ![]() для
для
большинства материалов значительно
меньше статического коэффициента
трения ![]() .
.
Этим объясняется то,
что в технике, когда это возможно,
стремятся заменить скольжение качением
(колеса, катки, шариковые подшипники и
т. п.).
24.Понятие
о фермах и их классификация
При
больших пролетах и значительных нагрузках
балки сплошного сечения становятся
экономически невыгодными. В таких
случаях их заменяют сквозной конструкцией
– стержневой системой (фермой), элементы,
которых при узловых нагрузках работают
на центральное сжатие и растяжение.
Фермой
называется геометрически неизменимая
система, составленная из стержней,
шарнирно соединенных между собой.
При
расчетах ферм принимают, что узлы
являются идеально гладкими, лишенными
трения, а оси всех стержней проходят
через геометрические центры шарниров.
Такой
расчетной схемой будем пользоваться
на протяжении дальнейшего расчета.
На
практике обычно ферме придают такое
устройство, чтобы нагрузка передавалась
на нее исключительно в узлах. При таком
устройстве любая нагрузка будет вызывать
в любом стержне только продольные
усилия.
Кроме плоских ферм,
у которых оси всех стержней расположены
в одной плоскости, применяются пространственные фермы,
оси элементов которых не лежат в одной
плоскости. Расчет пространственных
ферм часто удается свести к расчету
нескольких плоских ферм.
Расстояние
между осями опор фермы называется пролетом.
Стержни, расположенные по внешнему
контуру фермы, называется поясными, и
образуют пояса.
Стержни,
соединяющие пояса, образуют решетку
фермы и называются: вертикальные –
стойками, наклонные – раскосами.
Расстояние между соседними узлами
любого пояса фермы называется
панелью.
Стержни,
ограничивающие контур фермы сверху,
образуют ее верхний пояс, а снизу –
нижний. Внутренние стержни образуют
решетку, вертикальные стержни которой
называется стойками, наклонные –
раскосами. Расстояние по горизонтами
м/у соседними узлами любого пояса
называется длиной панели.
Классификация:
1)
по очертаний поясов;
2) по типу решетки:
раскосные, полураскосные, многораскосные
с треугольными решетками, с составной
(шпренгельной) решеткой;
3) по назначению
– мостовые, стропильные, башенные и
т.д;
4) по условию опирания – балочные,
арочные, консольные, балочно-консольный.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Силой трения называют обратное усилие, распределенное по площади контакта соприкасающихся твердых тел, возникающее при движении или удержании в равновесии одного тела относительно другого.
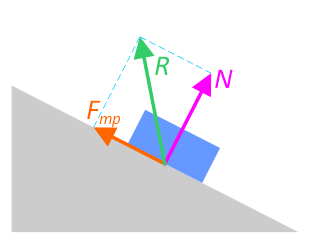
Рисунок 1
При стремлении сдвинуть тело, лежащее на шероховатой поверхности, возникает сила реакции R, которая имеет две составляющие – нормальную N и силу трения Fmp (рисунок 1).
В теоретической механике обычно рассматривается только сухое трение между поверхностями, при этом различают трение при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.
Сила трения скольжения
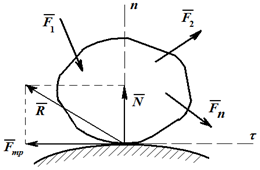
Рисунок 2
При покое сила трения скольжения зависит только от активных сил и может быть определена (рисунок 2) как:
Fmp=∑Fiτ. (2.49)
В результате экспериментальных исследований французскими учеными Гийомом Амонтоном и Шарлем Кулоном были установлены законы для сухого трения:
- сила трения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Величина силы трения зависит от активных сил и заключена между нулем и своим максимальным значением, которое достигается в момент выхода тела из положения равновесия:
0 ≤ Fmp ≤ Fmpmax;
- максимальное значение силы трения при прочих равных условиях не зависит от площади контакта трущихся поверхностей и пропорционально нормальной реакции:
Fmpmax=fN [Н],
где f – коэффициент трения, являющийся безразмерной величиной и зависящий от материала и физического состояния трущихся поверхностей.
Угол трения
Если твердое тело под действием активных сил находится на шероховатой поверхности в предельном состоянии равновесия (сила трения достигает своего максимального значения), то полная реакция шероховатой поверхности отклонена от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол φ, который называют углом трения (рисунок 3). При этом
tgφ=Fmpmax/N=fN/N=f. (2.50)
То есть тангенс угла трения равен коэффициенту трения.
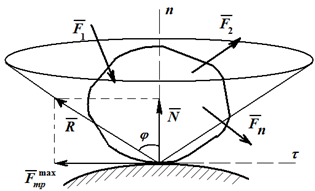
Рисунок 3
Конус трения
Конусом трения называют конус, описанный линией действия полной реакции, построенной на максимальной силе трения, вокруг направления нормальной реакции.
Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину.
Сила трения качения
Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.
Вследствие деформации тел их касание происходит вдоль площадки AB, появляется распределенная система сил реакций, которая, согласно основной теореме статики, может быть заменена силой и парой сил (рисунок 4).
Сила раскладывается на две составляющие – нормальную N и силу трения Fmp, пара сил называется моментом сопротивления качению MC.
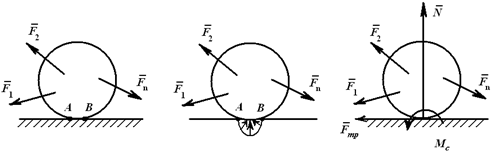
Рисунок 4
При равновесии тела момент сопротивления качению определяется из условий равновесия системы сил. При этом установлено, что момент сопротивления принимает значения от нуля до максимального значения. Максимальное значение момента сопротивления, соответствующее началу качения, определяется равенством
MC max=δN [Нм],
где δ – коэффициент трения качения, измеряемый в метрах и зависящий от материала контактирующих тел и геометрии зоны контакта.
Далее:
- Примеры решения задач >
- Равновесие при трении качения
- Трение на наклонной плоскости
- Трение скольжения
- Приведенный коэффициент трения
- Учет трения в механизмах
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее

Угол и конус трения
Представим себе тело, опирающееся на шероховатую поверхность (рис. 73). Если бы поверхность была абсолютно гладкой, то она представляла бы собой идеальную связь, действие которой на тело сводилось бы, как мы знаем, к одной лишь нормальной реакции. Если же опорная поверхность—шероховатая, то при наличии силы, стремящейся сдвинуть тело, появится еще сила трения, лежащая в касательной плоскости и направленная в сторону, противоположную той, в которую мы движем или пытаемся сдвинуть тело. Если мы будем рассматривать критический момент (когда тело будет находиться, так сказать, на грани между покоем и движением), то для этого случая сила трения будет иметь максимальное значение 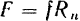 . Две составляющие реакции: нормальная
. Две составляющие реакции: нормальная 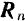 и касательная (сила трения)
и касательная (сила трения) 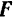 , складываясь по правилу параллелограмма, дадут полную реакцию
, складываясь по правилу параллелограмма, дадут полную реакцию 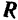 опорной поверхности, которая теперь будет уже составлять некоторый угол
опорной поверхности, которая теперь будет уже составлять некоторый угол 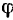 с нормалью к этой поверхности.
с нормалью к этой поверхности.
Наибольший угол 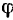 , на который вследствие трения отклоняется от нормали реакция
, на который вследствие трения отклоняется от нормали реакция 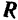 шероховатой поверхности, называется углом трения.
шероховатой поверхности, называется углом трения.
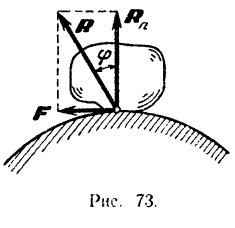
Из рис. 73 имеем:
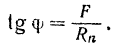
Но, как это видно из формулы (31),
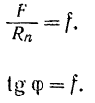
Тангенс угла трения равен коэффициенту трения скольжения.
Если мы рассматриваем тело, имеющее возможность перемещаться по шероховатой опорной поверхности в любом направлении, то линии действия возможных реакций  этой поверхности образуют (рис. 74) коническую поверхность.
этой поверхности образуют (рис. 74) коническую поверхность.
Конус, образующие которого наклонены под углом трения 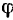 к нормали к поверхности скольжения в данной точке, называется конусом трения.
к нормали к поверхности скольжения в данной точке, называется конусом трения.
Если коэффициент трения при движении тела в различных направлениях по данной поверхности одинаков, то полная реакция этой поверхности отклоняется от нормали во всех направлениях на одинаковый угол трения 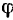 , и конус трения будет круглым с углом раствора
, и конус трения будет круглым с углом раствора 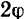 . Если же, как иногда бывает (например, при трении по дереву вдоль и поперек волокон), коэффициент трения при движении тела в разных направлениях имеет различные значения, то конус трения будет некруглым.
. Если же, как иногда бывает (например, при трении по дереву вдоль и поперек волокон), коэффициент трения при движении тела в разных направлениях имеет различные значения, то конус трения будет некруглым.
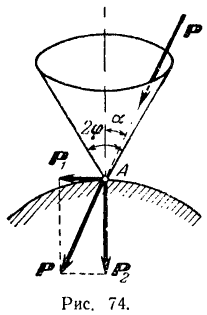
Пусть действующие на тело силы приводятся к одной равнодействующей силе 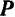 , проходящей через точку касания тела с поверхностью и образующей с нормалью к поверхности в этой точке угол
, проходящей через точку касания тела с поверхностью и образующей с нормалью к поверхности в этой точке угол 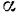 (рис. 74). Перенесем эту силу по линии ее действия в точку
(рис. 74). Перенесем эту силу по линии ее действия в точку 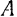 и разложим ее на две составляющие:
и разложим ее на две составляющие: 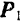 , лежащую в касательной плоскости, и
, лежащую в касательной плоскости, и 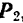 , направленную по нормали к поверхности. Тогда согласно формулам (31) и (32) максимальное значение силы трения покоя будет
, направленную по нормали к поверхности. Тогда согласно формулам (31) и (32) максимальное значение силы трения покоя будет
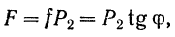
где 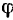 — угол трения, а
— угол трения, а 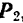 — модуль силы нормального давления тела на поверхность.
— модуль силы нормального давления тела на поверхность.
Модуль же силы 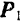 стремящейся заставить скользить тело по поверхности, будет
стремящейся заставить скользить тело по поверхности, будет
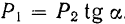
Для того чтобы тело оставалось на поверхности в равновесии, необходимо соблюдение условия 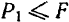 или, если подставить значения
или, если подставить значения 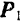 и
и 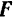 в это неравенство,
в это неравенство, 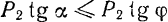 . Отсюда получаем, что условием равновесия тела на поверхности будет
. Отсюда получаем, что условием равновесия тела на поверхности будет
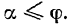
Если мы будем увеличивать модуль силы 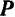 , оставляя неизменным ее направление, то пропорционально будет увеличиваться не только модуль
, оставляя неизменным ее направление, то пропорционально будет увеличиваться не только модуль 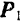 движущей силы, но и модуль
движущей силы, но и модуль 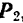 силы нормального давления, а это неизбежно влечет за собой и соответствующее увеличение силы трения, и тело по-прежнему будет оставаться в равновесии. Этим объясняются известные из практики явления заклинивания или самоторможения тел. Тело придет в движение лишь тогда, когда модуль силы
силы нормального давления, а это неизбежно влечет за собой и соответствующее увеличение силы трения, и тело по-прежнему будет оставаться в равновесии. Этим объясняются известные из практики явления заклинивания или самоторможения тел. Тело придет в движение лишь тогда, когда модуль силы 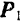 сделается больше, модуля силы
сделается больше, модуля силы 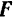 , а для этого нужно изменить направление силы
, а для этого нужно изменить направление силы 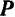 так, чтобы угол ос сделался больше угла трения
так, чтобы угол ос сделался больше угла трения 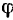 , т. е. чтобы сила
, т. е. чтобы сила 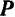 проходила вне конуса трения. Следовательно, если равнодействующая
проходила вне конуса трения. Следовательно, если равнодействующая 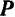 всех сил, приложенных к телу, каков бы ни был ее модуль, проходит внутри конуса трения, то тело остается в покос, возникновение движения возможно лишь в том случае, когда эта равнодействующая проходит вне конуса трения. Этим замечательным свойством области, заключенной внутри конуса трения, и вызвано его название.
всех сил, приложенных к телу, каков бы ни был ее модуль, проходит внутри конуса трения, то тело остается в покос, возникновение движения возможно лишь в том случае, когда эта равнодействующая проходит вне конуса трения. Этим замечательным свойством области, заключенной внутри конуса трения, и вызвано его название.
Пример задачи:
Плоскость 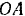 (рис. 75) вращается на шарнире
(рис. 75) вращается на шарнире  так, что ее можно установить, под любым углом к горизонту. На эту плоскость положено тело
так, что ее можно установить, под любым углом к горизонту. На эту плоскость положено тело 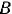 весом
весом 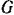 . При каком наибольшем угле
. При каком наибольшем угле 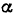 наклона плоскости тело будет оставаться в равновесии?
наклона плоскости тело будет оставаться в равновесии?
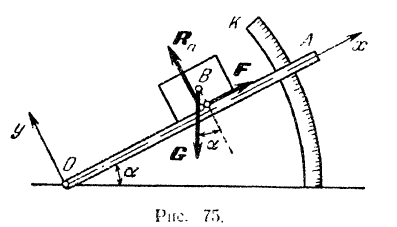
Решение:
Тело будет находиться на плоскости в равновесии под действием следующих сил: силы 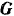 тяжести тела, нормальной реакции
тяжести тела, нормальной реакции 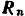 плоскости и силы трения
плоскости и силы трения 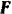 . Проектируя эти силы на выбранные координатные оси
. Проектируя эти силы на выбранные координатные оси 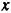 и
и 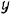 , получим уравнения равновесия
, получим уравнения равновесия
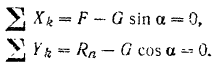
Из этой системы находим:
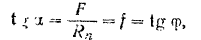
где 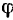 — угол трения. Для равновесии тела необходимо, следовательно, соблюдение условия
— угол трения. Для равновесии тела необходимо, следовательно, соблюдение условия
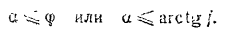
Найденная зависимость дает один из способов определения коэффициента трения скольжения в покое. Постепенно увеличивая угол наклона плоскости, замечаем (по шкале 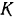 ) тот угол
) тот угол 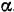 , при котором тело начинает скользить по плоскости. Тангенс этого угла дает нам коэффициент трения скольжения для соответствующих материалов (тела и плоскости).
, при котором тело начинает скользить по плоскости. Тангенс этого угла дает нам коэффициент трения скольжения для соответствующих материалов (тела и плоскости).
Аналогично решается задача об определении так называемого угла естественного откоса какого-либо грунта, т. е. наибольшего угла 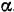 наклона грунта к горизонту, при котором частицы грунта, находящиеся на откосе, остаются в равновесии:
наклона грунта к горизонту, при котором частицы грунта, находящиеся на откосе, остаются в равновесии:
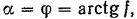
где 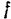 — коэффициент трения между частицами грунта.
— коэффициент трения между частицами грунта.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:




