Что такое время релаксации как его найти

Время релаксации — период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в раз ( — основание натурального логарифма), в основном обозначается греческой буквой .

Согласно принципу Ле Шателье — Брауна, при отклонении физической системы от состояния устойчивого равновесия возникают силы, которые пытаются вернуть систему к равновесному состоянию. Если в состоянии равновесия некоторая физическая величина имеет значение , причём отклонение от равновесия , то в первом приближении можно считать, что эти силы пропорциональны отклонению. Кинетическое уравнение для величины запишется в виде

,

где — некоторый параметр, а знак минус указывает на то, что реакция системы на возмущение приводит к возвращению к равновесному состоянию.

Время релаксации

В таком случае величина будет изменяться по закону:

,

где — начальное возмущение.

Использование[править | править код]

Приближение времени релаксации широко используется при описании кинетических процессов в физике, когда речь идет о кинетике установления равновесного состояния. Переход от неравновесного состояния к равновесию сопровождается диссипацией энергии и является необратимым процессом. Установление равновесия часто проходит в несколько этапов, которые характеризуются своими отдельными временами релаксации. Так, при возбуждении молекул светом установление теплового равновесия происходит за время порядка с, а вот люминесценция — излучение света возбуждёнными состояниями, может иметь характерные времена порядка микросекунд и даже наносекунд.

При описании многих физических процессов время релаксации берётся как феноменологический параметр, однако в отдельных случаях его можно определить через параметры микроскопических процессов, таких как вероятность квантовомеханического перехода или сечение рассеяния.

См. также[править | править код]

• Постоянная времени
• Время жизни

Литература[править | править код]

• Время релаксации // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — 707 с. — 100 000 экз.
• Д. Н. Зубарев. Релаксация // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.

Время релаксации — период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в e раз (e — основание натурального логарифма), в основном обозначается греческой буквой τ.

Согласно принципу Ле Шателье — Брауна при отклонении физической системы от состояния устойчивого равновесия возникают силы, которые пытаются вернуть систему к равновесному состоянию. Если в состоянии равновесия некоторая физическая величина f имеет значение , причём отклонение от равновесия , то в первом приближении можно считать, что эти силы пропорциональны отклонению. Кинетическое уравнение для величины f запишется в виде

,

где λ — некоторый параметр, а знак минус указывает на то, что реакция системы на возмущение приводит к возвращению к равновесному состоянию.

Время релаксации

В таком случае величина f будет изменяться по закону:

,

где – начальное возмущение.

Использование

Приближение времени релаксации широко используется при описании кинетических процессов в физике, когда речь идет о кинетике установления равновесного состояния. Переход от неравновесного состояния к равновесию сопровождается диссипацией энергии и является необратимым процессом. Установление равновесия часто проходит в несколько этапов, которые характеризуются своими отдельными временами релаксации. Так, при возбуждении молекул светом установление теплового равновесия происходит за время порядка с, а вот люминесценция — излучение света возбуждёнными состояниями, может иметь характерные времена порядка наносекунд и даже микросекунд.

При описании многих физических процессов время релаксации берётся как феноменологический параметр, однако в отдельных случаях его можно определить через параметры микроскопических процессов, таких как вероятность квантовомеханического перехода или сечение рассеяния.

См. также

• Время жизни

 Время
релаксации τ – время,
в течение которого амплитуда А уменьшается
в   e    раз.
, 
тогда   
.

Т.к.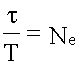  
 
– число колебаний за время , то:

коэффициент
затухания β есть
физическая величина, обратная
времени, в
течение которого амплитуда уменьшается
в е раз.

логарифмический
декремент затухания χ есть
физическая величина, обратная числу
колебаний, по истечении которых амплитуда
А уменьшается в e раз.

Добротность
колебательной системы – отношение
энергии, запасённой в колебательной
системе, к энергии, теряемой системой
за один период колебания. Добротность
характеризует качество колебательной
системы (См. Колебательные системы),
т.к. чем больше Д. к. с., тем меньше потери
энергии в системе за одно колебание. Д.
к. с. Q связана
с логарифмическим Декрементом затухания
δ; при малых декрементах затухания Q ≈
π/δ. В колебательном контуре с
индуктивностью L,
ёмкостью C и
омическим сопротивлением R Д.
к. с.

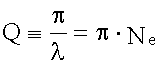
5. Каким образом гармонические колебания представляют методом векторной диаграммы? Сложение колебаний методом векторной диаграммы.

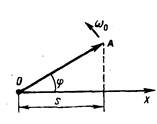
Гармонические
колебания изображаются графически методом
вращающегося век­тора амплитуды, или методом
векторных диаграмм. Для этого из
произвольной точ­ки О, выбранной
на оси х, под
углом , равным
начальной фазе колебания, откладыва­ется
вектор А, модуль которого равен
амплитуде Арассматриваемого
колебания (рис. 199). Если этот вектор
привести во вращение с угловой
скоростью ₀,
равной циклической частоте колебаний,
то проекция конца вектора будет
перемещаться по оси х и
принимать значения от –А до +А, а
колеблющаяся величина будет изменяться
со временем по закону s=A cos
(₀t+).
Таким образом, гармоническое колебание
мож­но представить проекцией на
некоторую произвольно выбранную
ось вектора амп­литуды А, отложенного
из произвольной точки оси под
углом , равным
начальной фазе, и вращающегося с угловой
скоростью ₀ вокруг
этой точки.

Метод
векторной диаграммы:

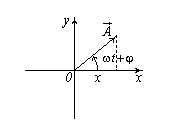
В
системе координат (x, y) рассмотрим
радиус-вектор
,
который вращается с угловой скоростью .
Проекция этого вектора на ось x изменяется
во времени по гармоническому закону

и
описывает гармонические колебания с
амплитудой A, циклической частотой  и
начальной фазой .

 Этот
метод очень удобен для описания сложения
колебаний одного направления и одинаковой
частоты .Пусть имеются два гармонических
колебания

 
, 

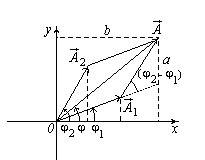
Надо
найти результат сложения этих колебаний:

 
,

т.е.
найти амплитуду результирующего
колебания A и его начальную фазу .
На векторной диаграмме гармонические
колебания x1 и x2 представим вращающимися
векторами 
 и 
.
Тогда результирующее колебание x будет
представляться вращающимся вектором 

Из
треугольника OAC по теореме косинусов
находим амплитуду результирующего
колебания

 
.

Из
чисто геометрических соображений можно
найти и начальную фазу результирующего
колебания :

Как
мы видим, результат сложения двух
колебаний существенно зависит от
разности фаз этих колебаний 1
– 2.
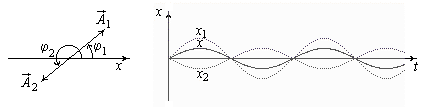
Рассмотрим два важных случая:

1
– 2
= 0 – колебания синфазные.

В
этом случае амплитуды колебаний
складываются, т.е. колебания усиливают
друг друга:

 
.

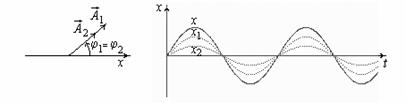
б) 1
– 2
=  – колебания
противофазные.

В
этом случае амплитуды колебаний
вычитаются, т.е. гасят друг друга:

 
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Если на колеблющееся тело действует сила трения, то энергия системы, амплитуда смещения и амплитуда скорости не остаются постоянными, а убывают, энергия расходуется на преодоление сил трения и превращается в тепло. Происходит затухание колебаний. Такие колебания не являются гармоническими, и дифференциальное уравнение движения, как это было показано в начале раздела, имеет вид:

,

где b = r/2m – коэффициент затухания,  – собственная частота (угловая) колебаний системы при отсутствии затухания и m – масса колеблющейся системы. При условии, что затухание мало β << ω₀, этому уравнению в качестве решения удовлетворяет функция (рис. 48):

,

где е = 2,71 – основание натуральных логарифмов; A₀ и a₀ – постоянные  величины, зависящие от начальных условий;  – угловая частота затухающих колебаний, которая всегда меньше собственной частоты ω₀.

 Периодом затухающих колебаний принято называть время T, за которое система дважды проходит через среднее положение в одном и том же направлении, или время, за которое отклонение в одну и ту же сторону дважды достигает максимального значения. Силы трения замедляют движение системы. Поэтому период затухающих колебаний всегда несколько больше, чем период тех собственных колеба­ний, которые совершала бы система, если бы трение отсутствовало. При малом трении β << w₀ можно считать, что период затухающих колебаний Т = 2p/w практически равен периоду колебаний в отсутствии трения Т₀ = 2p/w₀, и угловая частота затухающих колебаний w = 2p/T совпадает с угловой частотой в отсутствии трения w₀ = 2p/Т₀.

Роль  амплитуды  колебаний в условно периодическом движении играет величина, которая убывает с течением времени по экспоненциальному закону:

.

Коэффициентом затухания β определяется быстрота (скорость), с которой убывает амплитуда. Величина τ_с, обратная β, называется временем затухания или временем релаксации τ_с = 1/β. Время релаксации – это то время, в течение которого амплитуда уменьшается в е = 2,71 раз. В самом деле, при t = t_c имеем

A(0)/A(t_c) = A₀/(A₀e^–1) = e.

Отношение амплитуд, соответствующих различным моментам времени, отличающимся на период, называется декрементом затухания:

D = A(t)/A(t + T) = A₀ e^{–b t} /A₀ e^{–b (t + T )} = e ^{b T}

Натуральный логарифм этого отношения называется логарифмическим декрементом затухания:

J = ln D = ln e ^{b T} = b T =  T / t_c .

Показатель затухания β характеризует затухание колебаний за единицу времени, а логарифмический декремент – за период. Величина, обратная логарифмическому декременту затухания, равна числу колебаний N_e, совершающихся за время релаксации: J^–1 = t_c / T = N_e , причем за это время t_c амплитуда уменьшается в е раз. Для характеристики колебательной системы часто употребляется также величина

Q = π /J = π N_e ,

называемая добротностью колебательной системы. Добротность пропорцио­нальна числу колебаний N_e , совершаемых системой за время релаксации.

Параметры затухания b, t_с, J и Q связаны между собой взаимно-однозначными соотношениями, а именно:

J = p / Q = b Т = Т / t_с , b = 1 /t_с = J / Т = p / Q Т,

t_с = 1 / b = Т / J =  Q Т / p   и  Q = p / J = p /b Т = pt_с / Т.

                          Рис. 48                                                         Рис. 49

Чем медленнее затухают колебания Т << t_с, тем выше добротность контура. Добротность – это характеристика качества колеблющейся системы. Для справки, добротность электрического колебательного контура обычно не превышает значения 10³, камертона составляет примерно 10⁴, кристалла кварца может достигать значения 10⁸, и наивысшей добротностью обладает резонатор лазера (10¹² и выше).

ВРЕМЯ РЕЛАКСАЦИИ. 1. В общем значении — см. релаксация.[ …]

Процесс установления статистического равновесия в физической или физико-химической системе; в этом процессе величины, характеризующие состояние системы, асимптотически приближаются к своим равновесным значениям. Время релаксации — промежуток времени, в течение которого система, выведенная из состояния равновесия, изменит свое состояние на Д/(1—е-1), т. е. примерно на 63% того полного изменения Д/ состояния, на которое теоретически требуется бесконечное время. Так, если термометр, находящийся в равновесии со средой при температуре 7 переместить в среду с температурой Т + ДГ, то он примет температуру Т + АТ теоретически через бесконечное время; но изменение на ДГ(1—е [) произойдет через конечный промежуток времени, который и называется временем релаксации. Чем больше время релаксации, тем больше инерция прибора.[ …]

Время релаксации для этого выражения такое же, как и для уравнения (4.18), но амплитудный множитель иной.[ …]

ЭКОЛОГИЧЕСКОЕ ВРЕМЯ РЕЛАКСАЦИИ — см. Время экологическое релаксации.[ …]

Наиболее короткими являются времена релаксации, связанные с упругой деформацией в воде. Время релаксации диэлектрической дисперсии приблизительно на порядок больше времени упругой деформации. Процесс диэлектрической дисперсии связан с переориентацией частиц в электрическом поле и требует для своего осуществления освобождения их от водородных связей. С освобождением от связей с ближайшими соседями связан и процесс самодиффузии молекул. По-видимому, эти процессы надо характеризовать другим микроскопическим временем х2. Это время измеряется в экспериментах по неупругому рассеянию нейтронов. Время тн о-»н++он характеризует процесс диссоциации молекулы на ионы и является характеристикой межмолекулярного взаимодействия в воде, обусловленного переходами протонов от молекулы к молекуле.[ …]

Далее для простоты примем, что времена релаксации подземного стока всех континентов одинаковы: = t – const.[ …]

Симметричность выражения для времени релаксации относительно констант скорости прямой и обратной реакций встречается во многих случаях, и, как правило, константы скорости мономолекулярных реакций нельзя рассчитать, не определив предварительно равновесные концентрации А и В. Позже мы увидим, что если реакция вследствие присутствия второго реагента является не мономолекулярной, а псевдомономолекуляр-ной, то время релаксации будет зависеть от концентрации, что позволит устранить указанную выше трудность.[ …]

Замкнутая термодинамическая система за время релаксации обязательно придет в состояние равновесия. При этом происходят сглаживание градиентов, фазовые переходы и т.д.[ …]

Как и для обратимых реакций [уравнение (4.10)], время релаксации представляет собой сумму времен релаксаций для двух реакций.[ …]

Из (57) следует известное выражение (51) для времени релаксации. Заметим, что, согласно Френкелю [186], время релаксации также определяется формулой (51), но только X является не полярной, а суммарной проводимостью воздуха.[ …]

Если и —скорость движения фронта кристаллизации и т — время релаксации электрических процессов во льду, то в системе лед—вода образуется некоторая толщина льда их с емкостью С, во столько раз превышающей емкость двойного слоя Сэ ф, во сколько раз их больше й, т. е.[ …]

С увеличением содержания воды от 12,5 до 148% более длинное время релаксации Т Т ) растет почти линейно от 160 до 250 мс. Более короткое время Т (Тп) с увеличением количества воды несколько возрастает, но при содержании воды более 40%, что соответствует 25 мс, перестает меняться. Зависимости как Тп, так и Т12 от обратной абсолютной температуры представляют собой прямые линии. На основании этих данных был сделан вывод, что существуют два разных состояния адсорбированной воды. Одно, сравнительно подвижное, характеризуется более длинным временем релаксации эта вода не связана непосредственно с целлюлозой, а образует, вероятно, водородные связи с другими молекулами воды. Второму состоянию соответствует более короткое время 7П; это прочно связанная вода, которая образует водородные связи с гидроксильными группами целлюлозы. Времена корреляции т„, связанные с Т ц и Т-.2, были определены на основе теории Бломбергена — Переела — Паунда (БПП) [25], развитой Кубо и Томита [36]. Величины тп согласуются с величинами та, временами корреляции, вычисленными на основании диэлектрических измерений. С увеличением содержания воды значения времени сиин-спиновой релаксации Т2 менялись от 0,5 до 4,5 мс. Если механизмы спин-спиновой и спин-решеточной релаксации одинаковы, то теория БПП предсказывает, что Т = Та.[ …]

Попытка определить величину проводимости по данным измерений времени релаксации поля после разрядов молнии у поверхности земли была предпринята Фрайером [302] для дипольной модели грозового облака. Он провел наблюдения над изменением поля после грозовых разрядов в Нью-Мексико (США) и определил время релаксации поля для ряда случаев на основании этой модели. Фрайер получил значение т = 15±10 с и среднее значение >,= = 5,8 • 10-13 См/м. Интерпретируя данные наблюдений Уормеля [587] подобным образом, он получил т = 10 с и Я = 9 10 13 См/м. Таким образом, Фрайер также пришел к выводу, что проводимость в грозовых облаках высока.[ …]

Впоследствии В. П. Докучаев отметил [48], что необходимо учитывать весьма малое время релаксации свободных зарядов в слое Е и предложил иную форму уравнений магнитной гидродинамики для описания потоков ионизированного воздуха в елоеЕ. Но это уточнение решения задачи не отразилось на практических выводах из анализа: в зависимости от концентрации ионов в слое Е потоки должны так или иначе отклоняться от направления чисто гео-строфического ветра, причем отклонения возможны в обе стороны. Что касается слоя F, то там на основании [47] и [48] надо учитывать весьма большую ионизацию и ничтожно малую плотность атмосферы, исключающую представление о ветре в обычном смысле этого слова: до настоящего времени еще неясно, указывают ли современные методы наличие какого-то упорядоченного движения воздуха в слое F или они дают возможность следить лишь за ка-кими-то пульсациями «ионных облаков».[ …]

Измерения всех параметров проводились непрерывно вдоль всего маршрута. Учитывая время релаксации приборов, равное примерно 50 с (на уровне 90%), были сформированы два ряда данных: осредненные по времени с шагом 1 мин. и осредненные по пройденному расстоянию с шагом 1 км. Эти ряды позволяют решать разнообразные задачи от оценки крупномасштабных континентальных особенностей распределения примесей до влияния на озон и окислы азота отдельных объектов. В настоящей работе мы рассмотрим лишь наиболее характерные особенности полученных распределений.[ …]

Коэффициент а в ранних работах по изучению уровенного режима Каспия принимали равным 0,02-0,03 (время релаксации моря 30-50 лет), потом с учетом оттока воды в залив Кара-Богаз-Гол – 0,075 (13 лет) на высокой отметке -25,5 м абс. и 0,05 (20 лет) на низкой отметке -28,3 м абс. Определение времени релаксации, исходя из данных наблюдений за уровнем моря (было построено регрессионное соотношение между ежегодными приращениями уровня и уровнем), дало на порядок большую величину, чем априорное – 150 лет (!).[ …]

Подход географический. ГЕОГРАФИЧЕСКИЙ ЭЛЕМЕНТ — см. Элемент географический. ГЕОГРАФИЧЕСКОЕ ВРЕМЯ РЕЛАКСАЦИИ — см. Время географическое релаксации. ГЕОГРАФИЧЕСКОЕ ПРОСТРАНСТВО РЕЛАКСАЦИИ — см. Пространство географическое релаксации.[ …]

Нестационарные тепловые методы накачки. При использовании этих методов накачки необходимо учитывать время заселения и время релаксации различных уровней. Практически они реализуются при использовании ударных волн или адиабатического расширения газовой смеси (газодинамические лазеры) [12, 14]. С помощью этих методов можно увеличить на 3 — 5 порядков плотность съема мощности с единицы объема по сравнению со стационарным электрическим разрядом (рис. 9.9). Использование ударных волн (быстрый нагрев) позволяет получить высокие скорости нагрева 104 — 105 К/с. Если время заселения тп уровня 3 меньше времени заселения уровня 2 (т13<т12), то между уровнями 2, 3 создается инверсная населенность. Ударные волны позволяют работать в импульсном режиме. При использовании быстрого охлаждения (адиабатического расширения газовой смеси при ее продуве через сопло Лаваля или щель) при условии т31>т21 населенность уровня 3 будет больше населенности уровня 2, т.е. возникает инверсная населенность. Использование адиабатического расширения (рис. 9.9, 6) позволяет создавать мощные газодинамические лазеры непрерывного или квазинепрерывного действия.[ …]

Набор этих коэффициентов показывает, насколько сильно испарение с поверхности водосбора; характерное время релаксации и коэффициент сопротивления движению воды в бассейне зависят от влагозапаса.[ …]

Для изменения свойств гидродисперсии рекомендуется обрабатывать систему импульсами с длительностью, превышающей время релаксации ионной сферы, что соответствует правой части выражения (3.137).[ …]

Предложено использовать для электрообработки сточных вод разряд, обладающий при малой мощности большой длительностью импульса, превышающей время релаксации ионной сферы дисперсных частиц. Нахождение суспензий в зоне разряда в течение нескольких секунд приводит к омещению кривой распределения частиц по крупности в сторону больших- размеров частиц. Частицы образуют устойчивые цепочечные агрегаты, время жизни которых составляет десятки и даже сотни секунд.[ …]

В области низких частот колебаний при увеличении частоты диэлектрическая проницаемость полярных диэлектриков остается постоянной до тех пор, пока время релаксации дипольных молекул остается меньше полупериода электрического поля (//2), поскольку за это время диполи успевают полностью упорядочиться в направлении поля.[ …]

В. Е. Зеленков, А. А. Мусина и В. К. Кульсартов установили изменение (возрастание) электропроводности природной воды после магнитной обработки; в их опытах время релаксации составило 8—10 ч. Анализ частотных характеристик импеданса и фазового сдвига электродно-химической поляризации свидетельствовал о значительном увеличении подвижности ионов — зарядо-носителей [52].[ …]

Нахождение общего решения для этого случая мы отложим до разд. 6. Здесь же рассмотрим ситуацию, когда одна из стадий протекает гораздо быстрее другой. При таких условиях времена релаксации для двух стадий существенно различаются и не налагаются друг на друга.[ …]

Для градовой модели максимальный заряд крупы, по Мейсону, равен 3,7- 10 10 Кл, а средний 7- 10 и Кл. В такой модели проводимость воздуха может, по-видимому, достигать 10-12 См/м, так что время релаксации (100—200 с) значительно меньше времени накопления заряда на крупе. Если принять, что интенсивность осадков (града и дождя) в градовой модели составляет 300 мм/ч, то средняя концентрация ледяных частиц в облаке сухого роста равна приблизительно 2 м 3. Тогда на границе сферы радиусом 500 м напряженность поля не будет превышать 2,5 X X Ю3 В/м.[ …]

Полярные жидкости представляют особый интерес с точки зрения нашей гипотезы. Соседние молекулы разных жидкостей при образовании заряженного облака обладают разной подвижностью (времена релаксации различны). Для ответа на вопрос об ускорении подобных реакции необходимо исследовать влияние этого фактора на энергию диполей. Пока можно лишь предположить, что основную роль здесь играет тот факт, что диполи соседних молекул двух типов ориентированы в одном направлении.[ …]

При низких температурах ориентация молекул электрическим полем затруднена, поэтому диэлектрическая проницаемость невелика. При повышении температуры вследствие уменьшения вязкости время релаксации уменьшается. Ориентация молекул в таких условиях облегчается, что приводит к увеличению интенсивности дипольно-релаксационной поляризации и резкому росту диэлектрической проницаемости. После достижения максимума она уменьшается (приблизительно обратно пропорционально температуре) за счет роста теплового движения молекул, препятствующего упорядочению полярных молекул (диполей).[ …]

Установлено, что применение омагничивания приводит к значительной (до 40%) интенсификации крашения (увеличению выхода красителя на ткани), но только при оптимальных режимах магнитной обработки. Время релаксации свойств воды после ее пребывания в магнитном поле таково: через 3 ч активность воды заметно снижается, через 6 ч прирост накрашивания (по отношению к контрольному образцу) равен нулю [250, с. 94].[ …]

Высокоэластическая деформация обусловлена гибкостью макромолекул, т. е. способностью легко менять конформации. Высокоэластическая деформация эластомеров — ярко выраженный релаксационный процесс. Время релаксации для звеньев полимерных цепей составляет 10-4-— 10—6 с (в 104—107 раз выше, чем у низкомолекулярных соединений). Для релаксационного процесса высокоэластической деформации характерен гистерезис (под гистерезисом обычно понимают отставание обратного процесса от прямого). Деформационные кривые, полученные при увеличении и снятии нагрузки, не совпадают. Кривая обратного процесса — снятия нагрузки 2 отстает от кривой прямого процесса — увеличения нагрузки 1 (рис. 9). При этом после снятия нагрузки образец полимера полностью не восстанавливает свои первоначальные размеры и форму. Наблюдается некоторая остаточная (пластическая) деформация.[ …]

Благодаря достаточно большой электропроводности льда электрические процессы, например распределение свободных зарядов по поверхности, протекают на ледяных частицах так же, как и на жидких каплях. Для оценки времени релаксации, необходимого для протекания процесса, можно использовать выражение (51). Подставляя в (51) значения для льда при 0 = —10° С и v = 50 Гц, а именно е = 2,4 10-10 Ф/м и х= 1Д См/м [180], получаем 10 3 с. Рассмотрим время релаксации заряда на ледяной сферической частице, находящейся в газовой среде с проводимостью к. Согласно Я. И. Френкелю [186], это время релаксации также определяется выражением (51). В атмосфере на уровне изотермы —10° С, который для умеренных широт летом соответствует высоте около 5 км, электропроводность имеет порядок 10 14 См/м. В грозовых облаках она составляет 10 “12 См/м. Подставляя эти значения в (51) и учитывая, что для воздуха б0 9- 10 12 Ф/м, получаем т=10- 103 с, т. е. оно на 2—4 порядка больше времени релаксации, необходимого для равномерного распределения зарядов до поверхности ледяной частицы.[ …]

Вообще, как это следует из сказанного выше, диффузия — это физический процесс установления равновесного распределения в пространстве тепла и плотностей любой субстанции. В замкнутой системе это равновесие устанавливается за время релаксации. В открытой системе, когда мы имеем дело с поступлением энергии или массы извне, формируются потоки энергии или вещества, при испарении — водяного пара.[ …]

Модель с сезонными колебаниями интегрировалась на 4,2 атмосферных года (с горизонтальным шагом в атмосфере 500 км в первые 3 года и 250 км в последние 1,2 года), синхронизированных с 1200 океанскими годами (с горизонтальным шагом в океане 500 км). Время релаксации в океанском блоке сокращалось путем искусственного усиления температурной и соленостной реакции глубоких слоев океана (на наибольших глубинах — впятеро). На более простой модели было проверено, что этот прием не искажает предельного статистически-равновесного состояния океана. Начальное состояние системы АОС бралось по результатам долгосрочного интегрирования модели со средней годовой инсоляцией (начинавшегося с сухой изотермической атмосферы с температурой 6,8 °С и однородного океана с температурой 2,5 °С и соленостью 34,8%о). Граничными условиями для атмосферного блока на поверхности океана служили данные о температуре ВПС и толщине морского льда, средние месячные значения которых накапливались в океанском банке, а для океанского блока — накапливавшиеся в атмосферном банке средние месячные значения потоков импульса и влаги, а также температура, отношение смеси водяного пара, скорость ветра и лучистый поток тепла на нижнем уровне в атмосфере (нужные для вычисления суммарного потока тепла — его прямое задание приводило к вычислительной неустойчивости).[ …]

И, наконец, пятым источником метастабильности водных систем является их микрогетерогенность, а следовательно существование развитых поверхностей раздела фаз. Сольватные оболочки воды, как показано Б. В. Дерягиным, имеют на несколько порядков меньшее время релаксации. Все изменения состояния ультрамикроско-пических твердых частиц и пузырьков газов (их слияние, рост или растворение) должны придавать воде метастабильность.[ …]

До сих пор возможность каких-либо изменений в воде под действием магнитных полей представляется фантастической. Принято считать, что вода и ее растворы практически не изменяют энергию в магнитных полях и нельзя ожидать каких-либо эффектов «памяти», так как время релаксации порядка 10“” с. Время же протока через обычно применяемые магнитные аппараты — десятые и сотые доли секунды, а индукция магнитных полей порядка 0,1 Тл. Все это конечно верно, но для идеальной, «неподвижной» жидкости, а такой нет в природе. Да и вода до сих пор, как и другие жидкости, приносит все новые сюрпризы.[ …]

Несколько исследований было проведено по изучению анизотропии молекул нитрата целлюлозы в растворе при ориентации внешним электрическим [214] или магнитным [189] полем и в отсутствие действия поля [18]. На основании таких измерений вычисляли диэлектрические и оптические свойства сегментов цепей. Определяли также времена релаксации ориентации цепи, которые хорошо совпадали с современными теоретическими представлениями по этому вопросу.[ …]

Сглаживание температурных неоднородностей изучалось также Спигэлом [5]. Несколько отличным от нашего методом он также получил дисперсионное уравнение (7). Его метод позволяет показать, что это уравнение верно и для трехмерного поля радиации в однородно поглощающей среде. Однако в выражении для характерного времени релаксации он использовал теплоемкость при постоянном объеме, а не при постоянном давлении, как этого требует механика сплошных сред [6]. Поэтому характерное время релаксации по Спигэлу получилось в 7 раз меньше, чем у нас, где 7 = ср/су — показатель адиабаты для рассматриваемого газа. Спигэл не решал, однако, каких-либо конкретных задач и не пытался определять функцию Грина, поэтому он не обратил внимания на тот факт, что радиационный механизм переноса тепла не может сглаживать разрывы, а лишь уменьшает экспоненциально со временем их интенсивность.[ …]

Каждый ион в воде обязательно взаимодействует с молекулами НгО, координируя их вокруг себя; говорят, что ион создает свою гидратную оболочку. По пути движения иона в растворе гидратная оболочка должна возникать непрерывно, в чем и заключается отличие от идеального газа. Интервал между столкновениями ионов называют временем релаксации; в это время происходят структурные изменения в растворе. Время релаксации в разбавленных растворах имеет порядок 10-9 с, т. е. структурные изменения восстанавливаются весьма быстро. Согласно классической теории, путь иона от столкновения до столкновения по аналогии с идеальным газом называется длиной свободного пробега. Самойлов оценивает ее в 100—1000 А, в зависимости от концентрации. Так как через каждые 50 А на пути иона может возникнуть участок льдоподобной микрофазы, то весьма вероятно, что при достаточно большой длине свободного пробега ион столкнется с полостью в каркасе и — если полость свободна — попадет в нее. При этом дальнейшее движение иона прекратится — вот и второе отличие от идеального газа. Разумеется, через какое-то время ион освободит полость и продолжит хаотическое тепловое движение. Но пока ион в полости,— мы это специально подчеркиваем — он неподвижен, он стабилизирован в полости сам и стабилизирует полость.[ …]

Имеющиеся данные не позволяют отдать предпочтение одному пз этих объяснений. Однако когда измерения диэлектрической постоянной или коэффициентов поглощения при более высоких частотах колебаний становятся возможными, это позволяет сделать выбор между ними. Молекулы, не имеющие связей или имеющие одну связь, будут характеризоваться временами релаксации равными или большими, чем время релаксации 1,0 • 10-12 с, наблюдаемое для воды в разбавленном растворе бензола (табл. 4.5). Наоборот, заторможенные трансляционные и лпбрациопные движения молекул воды имеют полосы поглощения около 200 и 700 см-1 и поэтому должны вызывать дисперсию диэлектрической константы при частотах около 1013 с“1 (см. п. 4.7.3). Следовательно, имеется возможность провести различие между двумя механизмами при количественном определении диэлектрического или абсорбционного поведения жидкости в частотном интервале от 1012 до 1013 с-1.[ …]

Низкомолекулярное вещество при данной температуре может находиться в одном из трех физических (агрегатных) состояний: твердом, жидком или газообразном. При изменении температуры происходит перегруппировка молекул и вещество из одного равновесного состояния переходит в другое. Этот переход требует определенного времени. Процесс достижения равновесия во времени называется релаксацией, а время достижения равновесия — временем релаксации. У низкомолекулярных соединений время релаксации очень мало и практически не оказывает влияния на поведение вещества.[ …]

Колебательные состояния молекул воды, ответственные за комбинационное рассеяние, имеют время релаксации 10“‘1 с, поэтому сигнал КР линейно связан с интенсивностью возбуждающего излучения в очень широких пределах. При перестройке длины волны излучения для оптимального возбуждения флуоресцирующей примеси благодаря фиксированному сдвигу линии КР относительно линии возбуждающего излучения нормировка на сигнал КР может осуществляться в широком спектральном диапазоне.[ …]

И. М. Имянитов и Л. С. Мордовина [69] пытались объяснить большие значения разности потенциалов на границе лед—вода при кристаллизации растворов исходя из представления, что эффект Воркмена—Рейнольдса обусловливается контактной разностью потенциалов. Авторы [69] пришли к выводу, что на основании уравнения (64) можно объяснить большие разности потенциалов (порядка 10—102 В), которые наблюдаются в экспериментах, если учесть скорость движения фронта кристаллизации и время релаксации электрических процессов во льду.[ …]

Рассматриваемую ситуацию можно отличить от случая, когда быстрой является первая стадия, поскольку 1/т2 уменьшается с увеличением [Э]. Это легко понять, проведя аналогию с необратимыми и обратимыми реакциями [уравнения (4.1) и (4.10)]. Ясно, что, когда концентрация Э очень высока, реакция по существу необратима, поскольку форма Е полностью переводится в форму ЕБ и, следовательно, 1/т2 стремится к Аналогичным образом, когда [8]-»-0, концентрация ЕБ становится очень малой и 1/тг-»- к + к- . Следовательно, время релаксации зависит от концентрации.[ …]

Недавно (в феврале 1975 г.) X. Пенфильд [317 ] по наблюдениям вращательной линии излучения озона с Я = 2,71 мм ([ = 110,8 ГГц) смог изучить профили ВР озона днем и ночью в слое 50 … 80 км. Выяснилось, что выше 50 км содержание озона в течение 50 мин после восхода Солнца уменьшается вдвое, достигая в конце этого интервала времени 1016 молекул см 2. Это значит, что выше 50 км ммеется всего 0,37 Д. Е. озона—в 2,5 раза меньше, чем предсказывает формула (34.4). Это экспериментальное доказательство — хотя и единичное — дневного убывания озона в мезосфере очень важно Оно показывает, что время релаксации озона там очень невелико, и что озон в мезосфере должен находиться в состоянии фотохимического равновесия.[ …]