В вопросе не указано косинус от 5 градусов или 5 радиан нужно найти, поэтому рассмотрим оба варианта.
cos 5 градусов
Косинус 5 градусов можно найти с помощью таблиц Брадиса, которые позволяют определить значения наиболее часто использующихся тригонометрических функций от аргументов в диапазоне от 0 до 360 градусов.
Обращаясь к таблице узнаем, что косинус 5 градусов равен 0,996195.
Обратим внимание, что таблицы показывают значение с точностью до шести знаков после запятой.
Еще более простым вариантом является использование калькулятора, который покажет значение косинуса с большим количеством знаков после запятой, чем таблица Брадиса:
cos (5 gradusov) = 0,9961946981…..
cos 5 радиан
Если же необходимо вычислить значение косинуса от 5 радиан, то нужно перевести градусы в радианы с помощью формулы:
5 radian = 5 gradusov * 180 gradusov / Pi radian = 5* 57,3 = 286,5 radian.
Далее можно воспользоваться одним из выше рассмотренных способов. Например, с помощью калькулятора вычислим, что:
cos (5 radian) = 0,284015…
Наиболее часто необходимо вычислять тригонометрические функции от аргументов в градусах, но обращайте внимание на уточнение, если в качестве аргумента функции будет стоять радиан. Разница между результатами огромная.
Таблица косинусов, найти значения угла косинусов
Косинус угла представляет собой одну из тригонометрических функций. Является соотношением ближнего к углу прямоугольного треугольника катета к гипотенузе. Записывается следующим образом: cos (А) = АС/АВ, где АС – ближний катет угла (А), АВ – гипотенуза.
Зачем необходимо производить такие сложные на первый взгляд вычисления? Еще с древних времен известна аксиома: знаю угол – знаю его тригонометрическую функцию. Соответственно, если известен cos любого угла, в таблице Брадиса можно найти этот угол. И наоборот – зная угол, не сложно вычислить косинус. Отсюда можно найти следующие данные: длина катетов и гипотенузы.
Эти данные используются не только в голых математических вычислениях. Невозможно составить даже элементарный план местности, не зная тригонометрических функций. Посредством онлайн калькулятора можно облегчить задачу и получать требуемые данные за доли секунды.
Таблица косинусов от 0° – 360°
|
|
|
|
|
|
|
|
|
|
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

The value of cos 5 degrees is 0.9961946. . .. Cos 5 degrees in radians is written as cos (5° × π/180°), i.e., cos (π/36) or cos (0.087266. . .). In this article, we will discuss the methods to find the value of cos 5 degrees with examples.
- Cos 5°: 0.9961946. . .
- Cos (-5 degrees): 0.9961946. . .
- Cos 5° in radians: cos (π/36) or cos (0.0872664 . . .)
What is the Value of Cos 5 Degrees?
The value of cos 5 degrees in decimal is 0.996194698. . .. Cos 5 degrees can also be expressed using the equivalent of the given angle (5 degrees) in radians (0.08726 . . .)
We know, using degree to radian conversion, θ in radians = θ in degrees × (pi/180°)
⇒ 5 degrees = 5° × (π/180°) rad = π/36 or 0.0872 . . .
∴ cos 5° = cos(0.0872) = 0.9961946. . .

Explanation:
For cos 5 degrees, the angle 5° lies between 0° and 90° (First Quadrant). Since cosine function is positive in the first quadrant, thus cos 5° value = 0.9961946. . .
Since the cosine function is a periodic function, we can represent cos 5° as, cos 5 degrees = cos(5° + n × 360°), n ∈ Z.
⇒ cos 5° = cos 365° = cos 725°, and so on.
Note: Since, cosine is an even function, the value of cos(-5°) = cos(5°).
Methods to Find Value of Cos 5 Degrees
The cosine function is positive in the 1st quadrant. The value of cos 5° is given as 0.99619. . .. We can find the value of cos 5 degrees by:
- Using Trigonometric Functions
- Using Unit Circle
Cos 5° in Terms of Trigonometric Functions
Using trigonometry formulas, we can represent the cos 5 degrees as:
- ± √(1-sin²(5°))
- ± 1/√(1 + tan²(5°))
- ± cot 5°/√(1 + cot²(5°))
- ±√(cosec²(5°) – 1)/cosec 5°
- 1/sec 5°
Note: Since 5° lies in the 1st Quadrant, the final value of cos 5° will be positive.
We can use trigonometric identities to represent cos 5° as,
- -cos(180° – 5°) = -cos 175°
- -cos(180° + 5°) = -cos 185°
- sin(90° + 5°) = sin 95°
- sin(90° – 5°) = sin 85°
Cos 5 Degrees Using Unit Circle
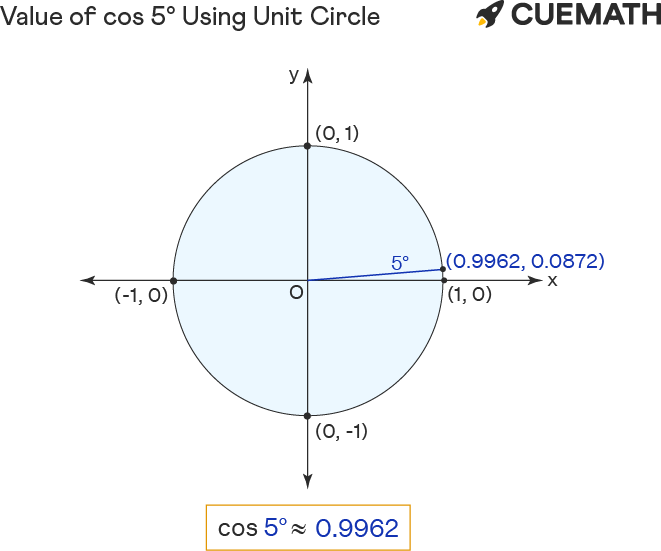
To find the value of cos 5 degrees using the unit circle:
- Rotate ‘r’ anticlockwise to form 5° angle with the positive x-axis.
- The cos of 5 degrees equals the x-coordinate(0.9962) of the point of intersection (0.9962, 0.0872) of unit circle and r.
Hence the value of cos 5° = x = 0.9962 (approx)
☛ Also Check:
- cos 0 degrees
- cos 11 degrees
- cos 90 degrees
- cos 19 degrees
- cos 85 degrees
- cos 8 degrees
FAQs on Cos 5 Degrees
What is Cos 5 Degrees?
Cos 5 degrees is the value of cosine trigonometric function for an angle equal to 5 degrees. The value of cos 5° is 0.9962 (approx)
What is the Value of Cos 5° in Terms of Sec 5°?
Since the secant function is the reciprocal of the cosine function, we can write cos 5° as 1/sec(5°). The value of sec 5° is equal to 1.003819.
How to Find Cos 5° in Terms of Other Trigonometric Functions?
Using trigonometry formula, the value of cos 5° can be given in terms of other trigonometric functions as:
- ± √(1-sin²(5°))
- ± 1/√(1 + tan²(5°))
- ± cot 5°/√(1 + cot²(5°))
- ± √(cosec²(5°) – 1)/cosec 5°
- 1/sec 5°
☛ Also check: trigonometry table
What is the Value of Cos 5 Degrees in Terms of Tan 5°?
We know, using trig identities, we can write cos 5° as 1/√(1 + tan²(5°)). Here, the value of tan 5° is equal to 0.087488.
How to Find the Value of Cos 5 Degrees?
The value of cos 5 degrees can be calculated by constructing an angle of 5° with the x-axis, and then finding the coordinates of the corresponding point (0.9962, 0.0872) on the unit circle. The value of cos 5° is equal to the x-coordinate (0.9962). ∴ cos 5° = 0.9962.
Косинус угла. Таблица косинусов.
Косинус угла через градусы, минуты и секунды
Косинус угла через десятичную запись угла
Как найти угол зная косинус этого угла
У косинуса есть обратная тригонометрическая функция – arccos(y)=x
cos(arccos(y))=y
Пример cos(60°) = 1/2; arccos(1/2) = 60°
Рассчитать арккосинус
Определение косинуса
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинусом угла α называется абсцисса точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
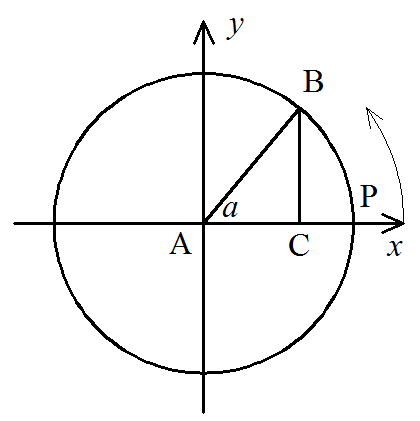
cos(α) = AC/AB
cos(-α) = cos(α)
cos(α ± 2π) = cos(α)
Таблица косинусов в радианах
cos(0°) = 1cos(π/12) = cos(15°) = 0.9659258263cos(π/6) = cos(30°) = 0.8660254038cos(π/4) = cos(45°) = 0.7071067812cos(π/3) = cos(60°) = 0.5cos(5π/12) = cos(75°) = 0.2588190451cos(π/2) = cos(90°) = 0cos(7π/12) = cos(105°) = -0.2588190451cos(2π/3) = cos(120°) = -0.5cos(3π/4) = cos(135°) = -0.7071067812cos(5π/6) = cos(150°) = -0.8660254038cos(11π/12) = cos(165°) = -0.9659258263cos(π) = cos(180°) = -1cos(13π/12) = cos(195°) = -0.9659258263cos(7π/6) = cos(210°) = -0.8660254038cos(5π/4) = cos(225°) = -0.7071067812cos(4π/3) = cos(240°) = -0.5cos(17π/12) = cos(255°) = -0.2588190451cos(3π/2) = cos(270°) = 0cos(19π/12) = cos(285°) = 0.2588190451cos(5π/3) = cos(300°) = 0.5cos(7π/4) = cos(315°) = 0.7071067812cos(11π/6) = cos(330°) = 0.8660254038cos(23π/12) = cos(345°) = 0.9659258263
Таблица Брадиса косинусы
| cos(0) = 1 | cos(120) = -0.5 | cos(240) = -0.5 |
| cos(1) = 0.9998476952 | cos(121) = -0.5150380749 | cos(241) = -0.4848096202 |
| cos(2) = 0.999390827 | cos(122) = -0.5299192642 | cos(242) = -0.4694715628 |
| cos(3) = 0.9986295348 | cos(123) = -0.544639035 | cos(243) = -0.4539904997 |
| cos(4) = 0.9975640503 | cos(124) = -0.5591929035 | cos(244) = -0.4383711468 |
| cos(5) = 0.9961946981 | cos(125) = -0.5735764364 | cos(245) = -0.4226182617 |
| cos(6) = 0.9945218954 | cos(126) = -0.5877852523 | cos(246) = -0.4067366431 |
| cos(7) = 0.9925461516 | cos(127) = -0.6018150232 | cos(247) = -0.3907311285 |
| cos(8) = 0.9902680687 | cos(128) = -0.6156614753 | cos(248) = -0.3746065934 |
| cos(9) = 0.9876883406 | cos(129) = -0.629320391 | cos(249) = -0.3583679495 |
| cos(10) = 0.984807753 | cos(130) = -0.6427876097 | cos(250) = -0.3420201433 |
| cos(11) = 0.9816271834 | cos(131) = -0.656059029 | cos(251) = -0.3255681545 |
| cos(12) = 0.9781476007 | cos(132) = -0.6691306064 | cos(252) = -0.3090169944 |
| cos(13) = 0.9743700648 | cos(133) = -0.6819983601 | cos(253) = -0.2923717047 |
| cos(14) = 0.9702957263 | cos(134) = -0.6946583705 | cos(254) = -0.2756373558 |
| cos(15) = 0.9659258263 | cos(135) = -0.7071067812 | cos(255) = -0.2588190451 |
| cos(16) = 0.9612616959 | cos(136) = -0.7193398003 | cos(256) = -0.2419218956 |
| cos(17) = 0.956304756 | cos(137) = -0.7313537016 | cos(257) = -0.2249510543 |
| cos(18) = 0.9510565163 | cos(138) = -0.7431448255 | cos(258) = -0.2079116908 |
| cos(19) = 0.9455185756 | cos(139) = -0.7547095802 | cos(259) = -0.1908089954 |
| cos(20) = 0.9396926208 | cos(140) = -0.7660444431 | cos(260) = -0.1736481777 |
| cos(21) = 0.9335804265 | cos(141) = -0.7771459615 | cos(261) = -0.156434465 |
| cos(22) = 0.9271838546 | cos(142) = -0.7880107536 | cos(262) = -0.139173101 |
| cos(23) = 0.9205048535 | cos(143) = -0.79863551 | cos(263) = -0.1218693434 |
| cos(24) = 0.9135454576 | cos(144) = -0.8090169944 | cos(264) = -0.1045284633 |
| cos(25) = 0.906307787 | cos(145) = -0.8191520443 | cos(265) = -0.08715574275 |
| cos(26) = 0.8987940463 | cos(146) = -0.8290375726 | cos(266) = -0.06975647374 |
| cos(27) = 0.8910065242 | cos(147) = -0.8386705679 | cos(267) = -0.05233595624 |
| cos(28) = 0.8829475929 | cos(148) = -0.8480480962 | cos(268) = -0.0348994967 |
| cos(29) = 0.8746197071 | cos(149) = -0.8571673007 | cos(269) = -0.01745240644 |
| cos(30) = 0.8660254038 | cos(150) = -0.8660254038 | cos(270) = 0 |
| cos(31) = 0.8571673007 | cos(151) = -0.8746197071 | cos(271) = 0.01745240644 |
| cos(32) = 0.8480480962 | cos(152) = -0.8829475929 | cos(272) = 0.0348994967 |
| cos(33) = 0.8386705679 | cos(153) = -0.8910065242 | cos(273) = 0.05233595624 |
| cos(34) = 0.8290375726 | cos(154) = -0.8987940463 | cos(274) = 0.06975647374 |
| cos(35) = 0.8191520443 | cos(155) = -0.906307787 | cos(275) = 0.08715574275 |
| cos(36) = 0.8090169944 | cos(156) = -0.9135454576 | cos(276) = 0.1045284633 |
| cos(37) = 0.79863551 | cos(157) = -0.9205048535 | cos(277) = 0.1218693434 |
| cos(38) = 0.7880107536 | cos(158) = -0.9271838546 | cos(278) = 0.139173101 |
| cos(39) = 0.7771459615 | cos(159) = -0.9335804265 | cos(279) = 0.156434465 |
| cos(40) = 0.7660444431 | cos(160) = -0.9396926208 | cos(280) = 0.1736481777 |
| cos(41) = 0.7547095802 | cos(161) = -0.9455185756 | cos(281) = 0.1908089954 |
| cos(42) = 0.7431448255 | cos(162) = -0.9510565163 | cos(282) = 0.2079116908 |
| cos(43) = 0.7313537016 | cos(163) = -0.956304756 | cos(283) = 0.2249510543 |
| cos(44) = 0.7193398003 | cos(164) = -0.9612616959 | cos(284) = 0.2419218956 |
| cos(45) = 0.7071067812 | cos(165) = -0.9659258263 | cos(285) = 0.2588190451 |
| cos(46) = 0.6946583705 | cos(166) = -0.9702957263 | cos(286) = 0.2756373558 |
| cos(47) = 0.6819983601 | cos(167) = -0.9743700648 | cos(287) = 0.2923717047 |
| cos(48) = 0.6691306064 | cos(168) = -0.9781476007 | cos(288) = 0.3090169944 |
| cos(49) = 0.656059029 | cos(169) = -0.9816271834 | cos(289) = 0.3255681545 |
| cos(50) = 0.6427876097 | cos(170) = -0.984807753 | cos(290) = 0.3420201433 |
| cos(51) = 0.629320391 | cos(171) = -0.9876883406 | cos(291) = 0.3583679495 |
| cos(52) = 0.6156614753 | cos(172) = -0.9902680687 | cos(292) = 0.3746065934 |
| cos(53) = 0.6018150232 | cos(173) = -0.9925461516 | cos(293) = 0.3907311285 |
| cos(54) = 0.5877852523 | cos(174) = -0.9945218954 | cos(294) = 0.4067366431 |
| cos(55) = 0.5735764364 | cos(175) = -0.9961946981 | cos(295) = 0.4226182617 |
| cos(56) = 0.5591929035 | cos(176) = -0.9975640503 | cos(296) = 0.4383711468 |
| cos(57) = 0.544639035 | cos(177) = -0.9986295348 | cos(297) = 0.4539904997 |
| cos(58) = 0.5299192642 | cos(178) = -0.999390827 | cos(298) = 0.4694715628 |
| cos(59) = 0.5150380749 | cos(179) = -0.9998476952 | cos(299) = 0.4848096202 |
| cos(60) = 0.5 | cos(180) = -1 | cos(300) = 0.5 |
| cos(61) = 0.4848096202 | cos(181) = -0.9998476952 | cos(301) = 0.5150380749 |
| cos(62) = 0.4694715628 | cos(182) = -0.999390827 | cos(302) = 0.5299192642 |
| cos(63) = 0.4539904997 | cos(183) = -0.9986295348 | cos(303) = 0.544639035 |
| cos(64) = 0.4383711468 | cos(184) = -0.9975640503 | cos(304) = 0.5591929035 |
| cos(65) = 0.4226182617 | cos(185) = -0.9961946981 | cos(305) = 0.5735764364 |
| cos(66) = 0.4067366431 | cos(186) = -0.9945218954 | cos(306) = 0.5877852523 |
| cos(67) = 0.3907311285 | cos(187) = -0.9925461516 | cos(307) = 0.6018150232 |
| cos(68) = 0.3746065934 | cos(188) = -0.9902680687 | cos(308) = 0.6156614753 |
| cos(69) = 0.3583679495 | cos(189) = -0.9876883406 | cos(309) = 0.629320391 |
| cos(70) = 0.3420201433 | cos(190) = -0.984807753 | cos(310) = 0.6427876097 |
| cos(71) = 0.3255681545 | cos(191) = -0.9816271834 | cos(311) = 0.656059029 |
| cos(72) = 0.3090169944 | cos(192) = -0.9781476007 | cos(312) = 0.6691306064 |
| cos(73) = 0.2923717047 | cos(193) = -0.9743700648 | cos(313) = 0.6819983601 |
| cos(74) = 0.2756373558 | cos(194) = -0.9702957263 | cos(314) = 0.6946583705 |
| cos(75) = 0.2588190451 | cos(195) = -0.9659258263 | cos(315) = 0.7071067812 |
| cos(76) = 0.2419218956 | cos(196) = -0.9612616959 | cos(316) = 0.7193398003 |
| cos(77) = 0.2249510543 | cos(197) = -0.956304756 | cos(317) = 0.7313537016 |
| cos(78) = 0.2079116908 | cos(198) = -0.9510565163 | cos(318) = 0.7431448255 |
| cos(79) = 0.1908089954 | cos(199) = -0.9455185756 | cos(319) = 0.7547095802 |
| cos(80) = 0.1736481777 | cos(200) = -0.9396926208 | cos(320) = 0.7660444431 |
| cos(81) = 0.156434465 | cos(201) = -0.9335804265 | cos(321) = 0.7771459615 |
| cos(82) = 0.139173101 | cos(202) = -0.9271838546 | cos(322) = 0.7880107536 |
| cos(83) = 0.1218693434 | cos(203) = -0.9205048535 | cos(323) = 0.79863551 |
| cos(84) = 0.1045284633 | cos(204) = -0.9135454576 | cos(324) = 0.8090169944 |
| cos(85) = 0.08715574275 | cos(205) = -0.906307787 | cos(325) = 0.8191520443 |
| cos(86) = 0.06975647374 | cos(206) = -0.8987940463 | cos(326) = 0.8290375726 |
| cos(87) = 0.05233595624 | cos(207) = -0.8910065242 | cos(327) = 0.8386705679 |
| cos(88) = 0.0348994967 | cos(208) = -0.8829475929 | cos(328) = 0.8480480962 |
| cos(89) = 0.01745240644 | cos(209) = -0.8746197071 | cos(329) = 0.8571673007 |
| cos(90) = 0 | cos(210) = -0.8660254038 | cos(330) = 0.8660254038 |
| cos(91) = -0.01745240644 | cos(211) = -0.8571673007 | cos(331) = 0.8746197071 |
| cos(92) = -0.0348994967 | cos(212) = -0.8480480962 | cos(332) = 0.8829475929 |
| cos(93) = -0.05233595624 | cos(213) = -0.8386705679 | cos(333) = 0.8910065242 |
| cos(94) = -0.06975647374 | cos(214) = -0.8290375726 | cos(334) = 0.8987940463 |
| cos(95) = -0.08715574275 | cos(215) = -0.8191520443 | cos(335) = 0.906307787 |
| cos(96) = -0.1045284633 | cos(216) = -0.8090169944 | cos(336) = 0.9135454576 |
| cos(97) = -0.1218693434 | cos(217) = -0.79863551 | cos(337) = 0.9205048535 |
| cos(98) = -0.139173101 | cos(218) = -0.7880107536 | cos(338) = 0.9271838546 |
| cos(99) = -0.156434465 | cos(219) = -0.7771459615 | cos(339) = 0.9335804265 |
| cos(100) = -0.1736481777 | cos(220) = -0.7660444431 | cos(340) = 0.9396926208 |
| cos(101) = -0.1908089954 | cos(221) = -0.7547095802 | cos(341) = 0.9455185756 |
| cos(102) = -0.2079116908 | cos(222) = -0.7431448255 | cos(342) = 0.9510565163 |
| cos(103) = -0.2249510543 | cos(223) = -0.7313537016 | cos(343) = 0.956304756 |
| cos(104) = -0.2419218956 | cos(224) = -0.7193398003 | cos(344) = 0.9612616959 |
| cos(105) = -0.2588190451 | cos(225) = -0.7071067812 | cos(345) = 0.9659258263 |
| cos(106) = -0.2756373558 | cos(226) = -0.6946583705 | cos(346) = 0.9702957263 |
| cos(107) = -0.2923717047 | cos(227) = -0.6819983601 | cos(347) = 0.9743700648 |
| cos(108) = -0.3090169944 | cos(228) = -0.6691306064 | cos(348) = 0.9781476007 |
| cos(109) = -0.3255681545 | cos(229) = -0.656059029 | cos(349) = 0.9816271834 |
| cos(110) = -0.3420201433 | cos(230) = -0.6427876097 | cos(350) = 0.984807753 |
| cos(111) = -0.3583679495 | cos(231) = -0.629320391 | cos(351) = 0.9876883406 |
| cos(112) = -0.3746065934 | cos(232) = -0.6156614753 | cos(352) = 0.9902680687 |
| cos(113) = -0.3907311285 | cos(233) = -0.6018150232 | cos(353) = 0.9925461516 |
| cos(114) = -0.4067366431 | cos(234) = -0.5877852523 | cos(354) = 0.9945218954 |
| cos(115) = -0.4226182617 | cos(235) = -0.5735764364 | cos(355) = 0.9961946981 |
| cos(116) = -0.4383711468 | cos(236) = -0.5591929035 | cos(356) = 0.9975640503 |
| cos(117) = -0.4539904997 | cos(237) = -0.544639035 | cos(357) = 0.9986295348 |
| cos(118) = -0.4694715628 | cos(238) = -0.5299192642 | cos(358) = 0.999390827 |
| cos(119) = -0.4848096202 | cos(239) = -0.5150380749 | cos(359) = 0.9998476952 |
Похожие калькуляторы
Подробная таблица косинусов углов
Содержание:
- Таблица косинусов в радианах
- Таблица косинусов от 0° до 180°
- Таблица косинусов от 181° до 360°
- Как пользоваться таблицей
Таблица косинусов в радианах
Радиан представляет собой угол, который соответствует дуге с длиной, определяемой радиусом.
В радианах принято измерять плоские углы.
Радианная мера является угловой мерой, измеряемой в радианах, определяется, как отношение рассматриваемого угла к радиану.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Проанализируем данное определение. Заметим, что справедливым является вывод о величине в 2 (pi) радиан, характерной для полного угла.
При решении задач по тригонометрии и геометрии часто приходится иметь дело с углами, измеряемыми в радианах. Упростить вычисление величин можно, если воспользоваться таблицей косинусов углов, для которых известна радианная мера. Кроме того, радианы нередко присутствуют в заданиях по различным темам математического анализа.

Таблица косинусов от 0° до 180°
Градусы, минуты и секунды являются общеизвестными измерительными единицами, предусмотренными для плоских углов. Угол в 360° соответствует одному полному обороту.
Градусы допустимо выражать в радианах и наоборот. Этот прием полезен для упрощения вычислений при решении задач с плоскими углами. Запишем справедливое соотношение, которое выражает зависимость между данными угловыми мерами:
(1^{circ }={frac {2pi }{displaystyle {360}}} радиан ={frac {pi }{displaystyle {180}}}={frac {1}{displaystyle {p}}}approx {frac {1}{displaystyle {57{,}295779513^{circ }}}}{displaystyle approx 0{,}0174532925})
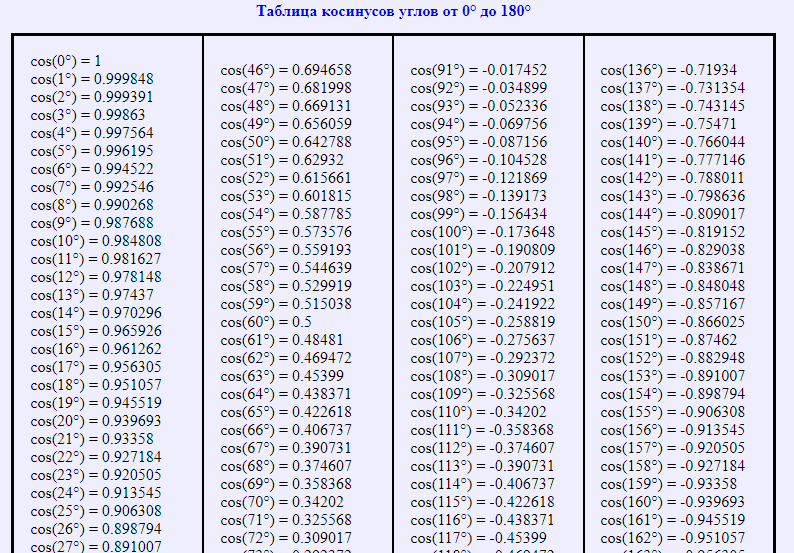

Таблица косинусов от 181° до 360°
Косинус представляет собой вид тригонометрической функции, демонстрирующей отношение прилегающего катета к гипотенузе.
В геометрических задачах принято вычислять тригонометрические функции, характерные для острого угла, по соотношениям сторон, которыми обладает прямоугольный треугольник. Предположим, что имеется некий треугольник АОВ с прямым углом. Обозначим в нем за гипотенузу сторону ОВ, а для острого угла запишем следующее равенство:
(angle AOB=alpha)
При таких исходных данных косинус можно вычислить по формуле:
(cos alpha ={frac {OA}{OB}})
Однако не во всех случаях вышеуказанное соотношение подходит для проведения вычислений. Значительно упростить решение тригонометрических задач можно, если воспользоваться таблицей косинусов:
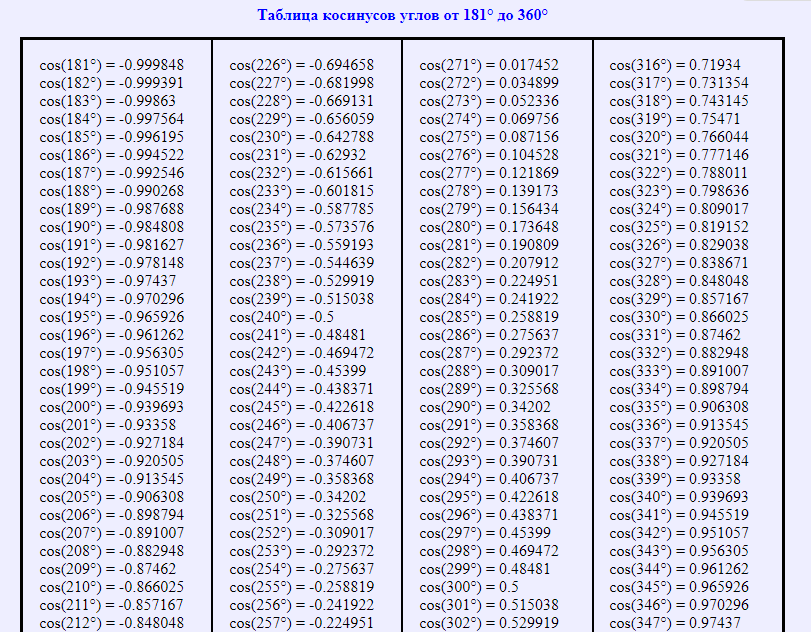
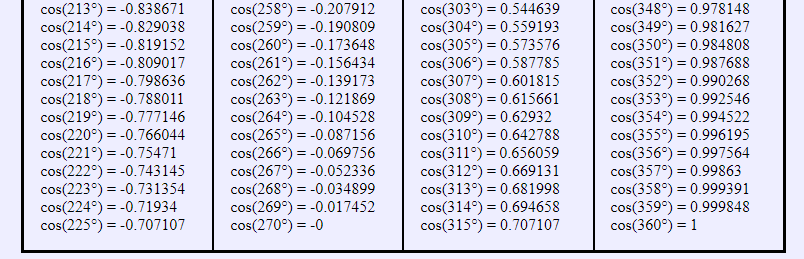
Как пользоваться таблицей
Таблица, в которой собраны значения косинусов для углов от 0° до 360°, либо углов, выраженных в радианной мере, является информационным материалом, который используют математики и физики. С помощью данного справочного пособия удается упростить и сократить решения разных задач по алгебре, геометрии, физике, математическому анализу, тригонометрии и другим дисциплинам, где приходится часто сталкиваться с массивными вычислениями.
Пользоваться рассматриваемой таблицей достаточно просто. Стандартный алгоритм действий ее применения в решении примеров состоит в выполнении нескольких ключевых операций:
- выявить тригонометрическую функцию в математическом соотношении;
- при необходимости требуется привести функцию к табличной форме;
- найти по таблице значение косинуса;
- путем подстановки известной величины продолжить математические преобразования и вычисления.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
