График функции «пол» (целая часть числа)
В математике, целая часть вещественного числа 


Обозначения и примеры[править | править код]
Впервые квадратные скобки (![[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)





В современной математике используются оба обозначения[6], ![[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)

![[x]equiv lfloor xrfloor =-3](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e41f712fa20152a524431a566d44a71b62f6ee0)
Определения[править | править код]
Функция «пол» 

Функция «потолок» 

Эти определения эквивалентны следующим неравенствам (где n — целое число):[7]
Свойства[править | править код]
В формулах, записанных ниже, буквами 



Пол и потолок как функции вещественной переменной[править | править код]
Функции пол и потолок отображают множество вещественных чисел в множество целых чисел:
Пол и потолок — кусочно-постоянные функции.
Функции пол и потолок разрывны: во всех целочисленных точках терпят разрывы первого рода со скачком, равным единице.
При этом функция пол является:
- полунепрерывной сверху и
- непрерывной справа.
Функция потолок является:
- полунепрерывной снизу и
- непрерывной слева.
Связь функций пол и потолок[править | править код]
Для произвольного числа 
Для целого 
Если 
Функции пол и потолок являются отражениями друг друга от обеих осей:
Пол/потолок: неравенства[править | править код]
Любое неравенство между вещественным и целым числами равносильно неравенству с полом и потолком между целыми числами
[7]:
Два верхних неравенства являются непосредственными следствиями определений пола и потолка, а два нижние — обращение верхних от противного.
Функции пол/потолок являются монотонно возрастающими функциями:
Пол/потолок: сложение[править | править код]
Целочисленное слагаемое можно вносить/выносить за скобки пола/потолка
[9]:
Предыдущие равенства, вообще говоря, не выполняются, если оба слагаемых — вещественные числа. Однако и в этом случае справедливы неравенства:
Пол/потолок под знаком функции[править | править код]
Имеет место следующее предложение:[10]
Пусть 
Тогда
всякий раз, когда определены 
В частности,
если 


Пол/потолок: суммы[править | править код]
Если 

[11]
Вообще, если 

Имеет место более общее соотношение
[12]:
Так как правая часть этого равенства симметрична относительно 

Разложимость в ряд[править | править код]
Тривиальным образом функция антье раскладывается в ряд с помощью функции Хевисайда:
где каждое слагаемое ряда создаёт характерные «ступеньки» функции. Этот ряд сходится абсолютно, однако ошибочное преобразование его слагаемых может привести к «упрощённому» ряду
который расходится.
Применение[править | править код]
Целочисленные функции пол/потолок находят широкое применение в дискретной математике и теории чисел. Ниже приведены некоторые примеры использования этих функций.
Количество цифр в записи числа[править | править код]
Количество цифр в записи целого положительного числа в позиционной системе счисления с основанием b равно
[13]
Округление[править | править код]
Ближайшее к 
Бинарная операция mod[править | править код]
Операция «остаток по модулю», обозначаемая 




,
а остаток
Дробная часть[править | править код]
Дробная часть вещественного числа 
Количество целых точек промежутка[править | править код]
Требуется найти количество целых точек в замкнутом промежутке с концами 


В силу свойств пол/потолка, это неравенство равносильно
.
Это есть число точек в замкнутом промежутке с концами 


Аналогично можно подсчитать количество целых точек в других типах промежутков. Сводка результатов приведена ниже
[14].
(Через 

Первые три результата справедливы при всех 

Теорема Рэлея о спектре[править | править код]
Пусть 

[15]
Тогда в ряду чисел
каждое натуральное 
Иными словами, последовательности
и
,
называемые последовательностями Битти, образуют разбиение натурального ряда.[16]
В информатике[править | править код]
В языках программирования[править | править код]
Во многих языках программирования существуют встроенные функции пола/потолка floor(), ceil().
В системах вёрстки[править | править код]
В TeX (и LaTeX) для символов пола/потолка 



Примечания[править | править код]
- ↑ Lemmermeyer, pp. 10, 23.
- ↑ Обозначение Гаусса использовали Cassels, Hardy & Wright и Ribenboim. Graham, Knuth & Patashnik и Crandall & Pomerance использовали обозначение Айверсона.
- ↑ Iverson, p. 12.
- ↑ Higham, p. 25.
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 88.
- ↑ Weisstein, Eric W. Floor Function (англ.) на сайте Wolfram MathWorld.
- ↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 89.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90-91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 93.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 108.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 112-117.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 91.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 95-96.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 99-100.
- ↑ А. Баабабов. «Пентиум» хорошо, а ум лучше // Квант. — 1999. — № 4. — С. 36-38.
См. также[править | править код]
- Дробная часть
- Округление
- Десятичный разделитель
Литература[править | править код]
- Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — 703 с. — ISBN 5-03-001793-3.
- М. К. Потапов, В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.
Целая часть числа – это наибольшее целое, не превосходящее данное.
С положительными числами просто, их целая часть – то стоит слева от запятой.
Для отрицательных чисел надо найти наибольшее целое, а (-5) > (-5,3). По числовой оси влево (в сторону убывания ) ближайшее целое равно -6. Оно и будет целой частью, так как (-6) < (-5,3)
[-5,3] = -6
А дробная часть равна разности между числом и его целой частью:
{-5,3} = (-5,3) – (-6) = -5,3 + 6 = 0,3
Т.е. целая часть число (-5,3) = (-6), а дробная 0,3. Она, как и положено, положительная.
Приложения:
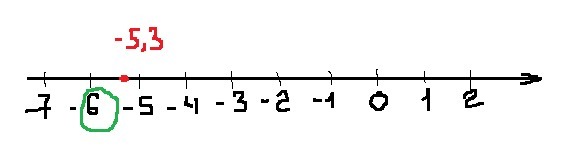
- Теория
- Практика
- Домашнее задание
- Дробные числа
- Операция деления с остатком
- Цикл if
IДробные числа
В прошлом уроке мы прошли целые числа: как они хранятся, считываются, выписываются и обрабатываются в языке программирования С/С++. Но в математике целые числа занимают лишь малую часть среди всех чисел. Потому что есть ещё и дробные числа, и они, конечно же, тоже есть и в языке программирования С/С++.
Хранение дробных чисел
Дробные числа хранятся в переменных типа double (от англ. double — двойной). Данный тип так называется, потому что для хранения дробного числа необходимо использовать две ячейки в памяти: для целой и для дробной части.
Целая часть числа
Целая часть [x] числа x – наибольшее целое число, не превосходящее x.
[3.273] = [3.989] = 3 \ [-3.273] = [-3.989] = -4
Для того, чтобы вычислить целую часть положительного числа в языке программирования С/С++, необходимо применить конвертацию переменной из типа double в тип int. Чтобы сконвертировать переменную типа double в тип int, необходимо просто поставить перед ней int и взять её в круглые скобки:
int(a);Для того, чтобы вычислить целую часть отрицательного числа в языке программирования С/С++, необходимо отнять единицу от числа, сконвертированного в тип int.
int(a) - 1;Дробная часть числа
Дробная часть {x} числа x – это разность x – [x] числа x и его целой части [x].
{3.273} = 3.273 – [3.273] = 3.273 – 3 = 0.273 \ {-3.273} = -3.273 – [-3.273] = -3.273 – (-4) = -3.273 + 4 = 0.727
Проще говоря, целая часть – то, что слева от точки, а дробная часть – то, что справа.
Для того, чтобы вычислить дробную часть числа в языке программирования С/С++, необходимо вычесть из этого числа его целую часть.
a - int(a);Но бывают дробные числа, дробная часть которых бесконечна. Такие числа хранятся в компьютере с некоторой точностью в силу невозможности хранить бесконечное число чисел.
Дробные числа в языке программирования могут также храниться в типе float, но его чаще всего не используют, так как он храните меньшее количество цифр после точки.
Создание переменной типа double
Чтобы создать переменную типа double:
double x; // создаём переменную типа doubleКак и в случае с целыми переменными, рекомендуется сразу же очищать переменную от мусора, присваиванием ей нулевое значение:
double x = 0.0; // создаём переменную типа doubleВ случае типа double необходимо присваивать значение именно 0.0, так как первый нуль очищает целую часть, а второй – дробную. Это правило хорошего тона.
Считывание дробных чисел с клавиатуры
Считывание дробных чисел с клавиатуры в языке программирования С/С++ происходит аналогично считыванию целых чисел с помощью функции scanf() за исключением другого типа данных (6 строка):
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
double x = 0.0; // создаём дробную переменную
scanf("%lf", &x); // считываем с клавиатуры дробное число в созданную переменную
return 0; // возвращаем 0 - успех
}Для типа double короткое имя при считывании это lf.
lf – образовано от словосочетания long float (длинное плавающее число – англ.) и подразумевает, что будет считано длинное дробное число.
Для типа float используется короткое имя f – от словосочетания float (плавающее число – англ.)
Вывод дробных чисел на экран
Вывод дробных чисел на экран в языке программирования С/С++ происходит аналогично выводу целых чисел с помощью функции printf() (7-8 строки):
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
double x = 0.0, y = 0.0; // создаём дробные переменные
scanf("%lf%lf", &x, &y); // считываем с клавиатуры дробные числа в созданные переменные
printf("x = %lfn", x); // выписываем значение переменной х
printf("The value of y is %fn", y); // выписываем значение переменной y
return 0; // возвращаем 0 - успех
}Формат вывода дробных чисел на экран
В языке программирования С/С++ можно регулировать, сколько цифр после точки будет выписано на экран. По умолчанию выписываются 6 цифр после точки.
Чтобы указать, сколько цифр после точки необходимо отобразить, можно написать следующий код (7-8 строки):
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
double x = 0.0, y = 0.0; // создаём дробные переменные
scanf("%lf%lf", &x, &y); // считываем с клавиатуры дробные числа в созданные переменные
printf("x = %.8lfn", x); // выписываем значение переменной х в формате 8 цифр после точки
printf("y = %.12lfn", y); // выписываем значение переменной y в формате 12 цифр после точки
return 0; // возвращаем 0 - успех
}Пример вывода данного кода:
23.2435345463423435467564534546574
23.4679475845847583958946849568
x = 23.24353455
y = 23.467947584585
Process returned 0 (0x0) execution time : 14.551 s
Press any key to continue.IIОперация деления с остатком
В языке программирования С/С++ есть операция деления с остатком. Более того, данная операция является очень популярной и широко используемой.
Определение оператора %
Для того, чтобы узнать остаток при делении одного числа на другое, существует специальный оператор, обозначающийся символом процента %:
c = a % b; // вычисляем остаток при делении переменной a на переменную b
printf("Remainder when dividing a number %d by a number %d is %dn", a, b, c); // выводим получившейся остаток на экранОстаток при делении отрицательных чисел
В математике принято, что остатки могут быть только положительными. Например, у числа -12 остаток 3 при делении на 5.
В языке программирования С/С++ остатки могут быть отрицательными. У числа -12 при делении на 5 остаток будет не 3, а -2. Необходимо иметь это в виду при решении зада
Процедура универсализации взятия остатка написана в данном уроке чуть ниже.
IIIЦикл if
Мы начинаем знакомство с таким объектом языка программирования С/С++, как цикл. В языке программирования С/С++ есть несколько основных базовых циклов.
Определение
Цикл – это функция, принимающая в качестве аргументов некоторые условия, а затем, в зависимости от истинности или ложности данных условий, запускающая или же не запускающая команды из своего тела.
Самым базовым циклом в языке программирования С/С++, как и во многих других высокоуровневых языках программирования, является цикл if (от англ. if – если).
Цикл if выполняет ровно то, что он означает: “Если условие в аргументе истинно, то команды из цикла будут выполнены, а если ложно – не будут”.
Разновидности условий
В качестве условий могут выступать совершенно любые математические выражения, которые могут быть абсолютно точно истинными или же абсолютно точки ложными. Например, условие “Среди чисел от 1 до 1000 есть число, которое делится на все положительные однозначные числа” указать в цикле if нельзя.
Условие должно быть односложным и легкопроверяемым компьютером с точки зрения вычисления. Условия могут быть как на созданные ранее переменные, так и на конкретные числа. Рассмотрим самые популярные разновидности условий:
Выражения со знаками:
В программировании существуют точно такие же знаки, что и в математике:
- Больше
> - Меньше
< - Больше или равно
>= - Меньше или равно
<= - Равно
== - Не равно
!=
Обратите внимание, что знак “равно” в условии цикла if состоит из двух символов равно ==. А знак “не равно” состоит из восклицательного знака !, который в языке С/С++ обозначает отрицание и символа равно: !=.
Условие пишется в круглых скобочках через пробел после названия цикла:
if (a > 3){} // условие, что переменная a больше числа 3
if (a >= b){} // условие, что переменная a больше или равна переменной b
if (a < b){} // условие, что переменная a меньше переменной b
if (b <= 10){} // условие, что переменная b меньше или равна числа 10
if (a == 5){} // условие, что переменная a равна числу 5
if (b != 12){} // условие, что переменная b не равна числу 12Выражения, требующие вычисления:
Но порой требуется сравнить не просто переменные или числа, а результаты некоторых операций над ними. Например, будет ли число a больше числа b после прибавления к нему числа c.
Для этого, конечно можно создать дополнительную переменную, положить в неё сумму, а потом уже сравнить эту сумму и число c в цикле if:
int sum_a_b = a + b; // создаём дополнительную переменную и кладём в неё сумму a и b
if (sum_a_b > c){} // проверяем, что сумма a и b больше cОднако это не очень удобно с точки зрения лишнего кода, а также использования памяти, необходимо для создания новой переменной.
Данное сравнение можно осуществить гораздо удобней, сразу сравнив результат суммы и число:
if (a + b > c){} // проверяем, что сумма a и b больше c сразу внутри цикла ifВнутри цикла if можно вычислять выражения любой сложности:
if ((3 * a + 2 * b) * (7 * c - 40) + 120 + (e + 10) * (e + 10) > a * b * c){} // проверяем сложные выраженияСамое главное правильно расставить скобки и соблюсти синтаксис языка С/С++.
Проверка делимости одного числа на другое:
Операция взятия остатка может пригодиться для проверки делимости одного числа на другое. Если число a делится на число b, то остаток при делении числа a на число b равен нулю.
Поэтому проверить делимость числа a на число b в программе можно следующим образом:
if (a % b == 0){ // проверяем, что остаток от деления числа a на число b равен нулю
printf("%d is divided by %dn", a, b); // выводим на экран, что число a делится на число b
}Сложные условия в цикле if:
Иногда необходимо проверить сразу несколько условий. Например, что число чётное и положительное. В таком случае можно воспользоваться двумя циклами if:
if (a % 2 == 0){ // проверяем, что число a чётное
if (a > 0){} // проверяем, что число a положительное
}Чтобы проверить, что число чётное, необходимо проверить на равенство нулю остаток при делении на 2.
Но иногда условия могут быть сложней: проверить, что число чётное, положительное и не делится на 7. И создавать для этого три вложенных друг в друга цикла if достаточно долго. Вместо этого можно воспользоваться одним циклом if со сложным условием, состоящем из нескольких простых:
if (a % 2 == 0 && a > 0 && a % 7 != 0){} // проверяем, что число a чётное, положительное и не делится на 7 в одном цикле ifДля связки простых условий можно использовать связки “И” или “ИЛИ”. Связка “И” обозначается двумя символами амперсанта &&, а связка “ИЛИ” – двумя вертикальными палочками ||. В примере выше использована связка “И”.
Чтобы в одном цикле if проверить, что число кратно 11 или 13, необходимо воспользоваться связкой “ИЛИ”:
if (a % 11 == 0 || a % 13 == 0){} // проверяем, что число a кратно 11 или 13Иерархия простых условий в составе сложного:
Важно понимать, что связка “ИЛИ” относится к связке “И” точно также, как операция сложения к операции умножения.
Допустим, необходимо проверить условие, что число положительное, чётное и при этом кратно или 11 или 13.
Можно написать просто:
if (a > 0 && a % 2 == 0 && a % 11 == 0 || a % 13 == 0){} // проверяем, что число a положительное, чётное и при этом кратно или 11 или 13 первым способомИ это будет неправильно. Перейдём от условий к выражениям с операциями сложения и умножения:
(a>0) times (a % 2 == 0) times (a % 11 == 0) + (a % 13 == 0)
Совершенно логично, что сначала будет произведено умножение, а только потом сложение полученного произведения с последним слагаемым. Но ведь нам необходимо, чтобы число гарантированно было чётно и положительно, и только потом кратно 11 или 13.
В стандартной арифметике для этого используются скобки:
(a>0) times (a % 2 == 0) times Big( (a % 11 == 0) + (a % 13 == 0)Big)
В языке программирования происходит тоже самое. Чтобы условие работало корректно, необходимо добавить скобки:
if (a > 0 && a % 2 == 0 && (a % 11 == 0 || a % 13 == 0)){} // проверяем, что число a положительное, чётное и при этом кратно или 11 или 13 вторым способомКонструкция else
Чаще всего необходимо сделать что-либо не только, когда выполнено условие, но и когда оно не выполнено. Использовать для этого второй точно такой же цикл if, только с противоположным условием не рационально.
Для этого и была придумана конструкция else, которая определяет область невыполнимости условия цикла if. Данная конструкция образована от слова else (иначе – англ.).
Допустим, необходимо разделить число на 2 и выписать его на экран, если оно чётное, и просто выписать его на экран, если нечётное. Для этого и нужно использовать else:
if (a % 2 == 0){ // проверяем, что число чётное
printf("%dn", a / 2); // делим его на 2 и выписываем на экран, если оно чётное
} else {
printf("%dn", a); // в противном случае просто выписываем его на экран
}Всё просто: “Если число a чётно, делим его на 2 и выписываем, иначе просто выписываем его”.
Конструкция else if
Данная конструкция может быть использована и в ещё более сложном условии. Например, необходимо сделать что-то конкретное, в зависимости от остатка при делении на 3. Так как при делении на 3 может быть три остатка (0, 1 и 2), обыкновенно конструкцией “если…иначе…” ограничиться нельзя. В таком случае можно воспользоваться:
if (a % 3 == 0){ // проверяем, что число имеет остаток 0 при делении на 3
// делаем что-то
} else if (a % 3 == 1){ // проверяем, что число имеет остаток 1 при делении на 3
// делаем что-то
} else { // если остаток при делении на 3 не 0 и не 1, то он точно 2, поэтому просто пишем else
// делаем что-то
}Взятие остатка от отрицательного числа
Как уже было замечено, в языке программирования С/С++ операция взятия остатка от отрицательных чисел работает не так, как принято у математиков. Если есть вероятность, что программному коду нужно будет работать с отрицательными числами, необходимо не просто брать остаток при делении одного числа на другое, а осуществлять проверку, с положительным или отрицательным числом идёт работа:
if (a > 0){
r = a % 5;
} else {
r = a % 5 + 5;
}В представленном выше коде осуществляется проверка знака переменной a и в случае, если число a отрицательно, чтобы остаток был таким, как принято у математиков, к остатку прибавляется то, число, на которое делится переменная a.
Однако можно поступить проще. Так как ясно, что в языке программирования С/С++ при делении с остатком отрицательных чисел получается остаток, равный разности принятого у математиков остатка и делителя.
Например, число -12 при делении на 5 в стандартной операции даст остаток -2, а в общепринятой – 3, а число 3 как раз получается прибавлением -2 и 5.
Таким образом, например, при нахождении чисел, имеющих остаток 4 при делении на 11, можно написать следующее условие в цикле if:
if (a % 11 == 4 || a % 11 == -7){
// делаем что-то
}1Задача №1.
Считать с клавиатуры два целых числа и вывести наибольшее из них.
Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
int x = 0, y = 0; // создаём целочисленные переменные
printf("Print 2 numbers:n"); // приглашаем пользователя на ввод
scanf("%d%d", &x, &y); // считываем два числа с клавиатуры
if (x > y){ // сравниваем числа
printf("%dn", x); // выписываем x
} else {
printf("%dn", y); // выписываем y
}
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 2 numbers:
12 9
12
Process returned 0 (0x0) execution time : 6.953 s
Press any key to continue.2Задача №2.
Считать с клавиатуры целое число, проверить его на чётность.
Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
int x = 0; // создаём целочисленные переменные
printf("Print 1 number:n"); // приглашаем пользователя на ввод
scanf("%d", &x); // считываем число с клавиатуры
if (x % 2 == 0){ // проверяем число x на чётность
printf("%d is divided by 2n", x); // выписываем, что x кратно двум
} else {
printf("%d is not divided by 2n", x); // выписываем, что x не кратно двум
}
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 1 number:
35
35 is not divided by 2
Process returned 0 (0x0) execution time : 2.372 s
Press any key to continue.3Задача №3.
Считать с клавиатуры два числа и проверить делится ли большее на меньшее.
Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
int x = 0, y = 0; // создаём целочисленные переменные
printf("Print 2 numbers:n"); // приглашаем пользователя на ввод
scanf("%d%d", &x, &y); // считываем числа с клавиатуры
if (x > y){ // сравниваем числа
if (x % y == 0){ // проверяем, что число x делится на число y
printf("%d is divided by %dn", x, y); // выписываем, что x кратно числу y
} else {
printf("%d is not divided by %dn", x, y); // выписываем, что x не кратно числу y
}
} else {
if (y % x == 0){ // проверяем, что число y делится на число x
printf("%d is divided by %dn", y, x); // выписываем, что y кратно числу x
} else {
printf("%d is not divided by %dn", y, x); // выписываем, что y не кратно числу x
}
}
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 2 numbers:
120 24
120 is divided by 24
Process returned 0 (0x0) execution time : 4.549 s
Press any key to continue.4Задача №4.
Считать с клавиатуры три целых числа и вывести наибольшее из них.
Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
int x = 0, y = 0, z = 0; // создаём целочисленные переменные
printf("Print 3 numbers:n"); // приглашаем пользователя на ввод
scanf("%d%d%d", &x, &y, &z); // считываем числа с клавиатуры
if (x > y && x > z){ // проверяем, что число x самое большое
printf("%dn", x); // выписываем наибольшее число
} else if (y > x && y > z){ // проверяем, что число y самое большое
printf("%dn", y); // выписываем наибольшее число
} else { // если это не x и не y, то это z
printf("%dn", z); // выписываем наибольшее число
}
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 3 numbers:
12 34 -19
34
Process returned 0 (0x0) execution time : 5.748 s
Press any key to continue.1Задача №1.
Считать с клавиатуры 4 целых числа и вывести наименьшее из них.
Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
int x = 0, y = 0, z = 0, w = 0; // создаём целочисленные переменные
printf("Print 4 numbers:n"); // приглашаем пользователя на ввод
scanf("%d%d%d%d", &x, &y, &z, &w); // считываем числа с клавиатуры
if (x < y && x < z && x < w){ // проверяем, что число x самое маленькое
printf("%dn", x); // выписываем наименьшее число
} else if (y < x && y < z && y < w){ // проверяем, что число y самое маленькое
printf("%dn", y); // выписываем наименьшее число
} else if (z < x && z < y && z < w){ // проверяем, что число z самое маленькое
printf("%dn", z); // выписываем наименьшее число
} else { // если это не x, не y и не z, то это w
printf("%dn", w); // выписываем наименьшее число
}
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 4 numbers:
12 20 19 -20
-20
Process returned 0 (0x0) execution time : 13.041 s
Press any key to continue.2Задача №2.
Считать с клавиатуры 3 целых числа и вывести их в порядке возрастания.
Порядок возрастания – это порядок, в котором каждое последующее число больше или равно предыдущего.
Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
int x = 0, y = 0, z = 0; // создаём целочисленные переменные
printf("Print 3 numbers:n"); // приглашаем пользователя на ввод
scanf("%d%d%d", &x, &y, &z); // считываем числа с клавиатуры
if (x < y && x < z){ // проверяем, что число x самое маленькое
if (y < z){ // сравниваем y и z
printf("%d %d %dn", x, y, z); // выписываем числа в порядке возрастания
} else {
printf("%d %d %dn", x, z, y); // выписываем числа в порядке возрастания
}
} else if (y < x && y < z){ // проверяем, что число y самое маленькое
if (x < z){ // сравниваем x и z
printf("%d %d %dn", y, x, z); // выписываем числа в порядке возрастания
} else {
printf("%d %d %dn", y, z, x); // выписываем числа в порядке возрастания
}
} else { // если самое маленькое не x и не y, то это z
if (x < y){ // сравниваем x и y
printf("%d %d %dn", z, x, y); // выписываем числа в порядке возрастания
} else {
printf("%d %d %dn", z, y, x); // выписываем числа в порядке возрастания
}
}
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 3 numbers:
28 -10 3
-10 3 28
Process returned 0 (0x0) execution time : 7.168 s
Press any key to continue.3Задача №3.
Считать с клавиатуры целое число и вывести на экран его последнюю цифру.
Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
int x = 0; // создаём целочисленные переменные
printf("Print 1 number:n"); // приглашаем пользователя на ввод
scanf("%d", &x); // считываем число с клавиатуры
printf("The last digit of %d is %dn", x, x % 10); // выписываем последнюю цифру числа x
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 1 number:
126
The last digit of 126 is 6
Process returned 0 (0x0) execution time : 1.585 s
Press any key to continue.4Задача №4.
Число подходящее, если оно нечётно и при этом имеет остаток 5 при делении на 8 или кратно 5. Считать с клавиатуры целое число и выписать, подходящее оно или нет.
Пример входных и выходных данных:
Пример числа, которое ввёл пользователь:
-13Пример корректного вывода программы для вышенаписанных входных данных:
-13 is a suitable numberРешение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
int x = 0; // создаём целочисленные переменные
printf("Print 1 number:n"); // приглашаем пользователя на ввод
scanf("%d", &x); // считываем число с клавиатуры
if (x % 2 != 0 && (x % 8 == 5 || x % 8 == -3 || x % 5 == 0)){
printf("%d is a suitable numbern", x); // выписываем, что это число подходящее
} else {
printf("%d is not a suitable numbern", x); // выписываем, что это число не подходящее
}
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 1 number:
-13
-13 is a suitable number
Process returned 0 (0x0) execution time : 1.689 s
Press any key to continue.5Задача №5.
Пользователь вводит одно число. Необходимо вывести его целую и дробную часть.
Пример входных и выходных данных:
Пример числа, которое ввёл пользователь:
-6.32Пример корректного вывода программы для вышенаписанных входных данных:
The integer part of -6.320000 is -7
The fractional part of -6.320000 is 0.680000Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
#include <math.h> // подключаем библиотеку math.h
int main(){ // создаём главную функцию
double x = 0.0, frac_x = 0.0; // создаём дробные переменные
int int_x = 0; // создаём целочисленную переменную
printf("Print 1 numbers:n"); // приглашаем пользователя на ввод
scanf("%lf", &x); // считываем дробное число
if (x < 0.0){ // если число отрицательно
int_x = int(x) - 1; // вычисляем целую часть
} else {
int_x = int(x); // вычисляем целую часть
}
frac_x = x - int_x; // вычисляем дробную часть
printf("The integer part of %lf is %dnThe fractional part of %lf is %lfn", x, int_x, x, frac_x); // выводим ответ
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 1 numbers:
12.7689
The integer part of 12.768900 is 12
The fractional part of 12.768900 is 0.768900
Process returned 0 (0x0) execution time : 2.856 s
Press any key to continue.6Задача №6.
Необходимо написать программу, которая сообщает пользователю, можно ли извлечь целочисленный корень из введённого им числа. Если можно, то программа сразу же извлекает его.
Для взятия квадратного корня в языке программирования С/С++ необходимо воспользоваться функцией sqrt() из библиотеки math.h.
Помните, что нельзя извлекать квадратный корень из отрицательного числа.
Чтобы проверить, целое число или нет, необходимо проверить на равенство нулю его дробную часть.
Пример входных и выходных данных:
Пример числа, которое ввёл пользователь:
16Пример корректного вывода программы для вышенаписанных входных данных:
The square root from 16.000000 is integer and is equal to 4.000000Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
#include <math.h> // подключаем библиотеку math.h
int main(){ // создаём главную функцию
double x = 0.0, sqrtx = 0.0; // создаём две дробные переменные
printf("Print 1 numbers:n"); // приглашаем пользователя на ввод
scanf("%lf", &x); // считываем дробное число
if (x < 0.0){ // если число отрицательное
printf("Cannot get the square root from negative number %lfn", x); // выводим, что нельзя брать квадратный корень из отрицательного числа
return 0; // возвращаем 0 - успех
}
sqrtx = sqrt(x); // вычисляем корень из числа пользователя
if (sqrtx - int(sqrtx) == 0.0){ // проверяем, что корень - целое число
printf("The square root from %lf is integer and is equal to %lfn", x, sqrtx); // выводим, что корень - целое число и сам корень
} else {
printf("The square root from %lf is not integern", x); // выводим, что корень - не целое число
}
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 1 numbers:
12
The square root from 12.000000 is not integer
Process returned 0 (0x0) execution time : 0.407 s
Press any key to continue.7Задача №7.
Пользователь вводит три дробных числа. Они интерпретируются, как коэффициенты a, b, c уравнения aх + b = c. Необходимо вывести на экран решение данного уравнения.
Помните, что делить на нуль нельзя.
Пример входных и выходных данных:
Пример чисел, которые ввёл пользователь:
2 4 7Пример корректного вывода программы для вышенаписанных входных данных:
Your equation is: (2.000000)x + (4.000000) = (7.000000)
The solution is 1,5Решение:
#include <stdio.h> // подключаем библиотеку stdio.h
#include <stdlib.h> // подключаем библиотеку stdlib.h
int main(){ // создаём главную функцию
double a = 0.0, b = 0.0, c = 0.0; // создаём три дробные переменные
printf("Print 3 numbers:n"); // приглашаем пользователя на ввод
scanf("%lf%lf%lf", &a, &b, &c); // считываем три дробных числа
printf("Your equation is: (%lf)x + (%lf) = (%lf)n", a, b, c); // выводим на экран уравнение
if (a == 0.0){ // если коэффициент а равен нулю
if (b == c){ // если коэффициент b равен коэффициенту с
printf("The solution is any numbern"); // выводим на экран решение
return 0; // возвращаем 0 - успех
} else { // иначе (если коэффициент b не равен коэффициенту с)
printf("The solution is the empty setn"); // выводим на экран решение
return 0; // возвращаем 0 - успех
}
}
printf("The solution is %lfn", (c - b) / a); // выводим на экран решение
return 0; // возвращаем 0 - успех
}Пример работы программы:
Print 3 numbers:
0 3 3
Your equation is: (0.000000)x + (3.000000) = (3.000000)
The solution is any number
Process returned 0 (0x0) execution time : 3.882 s
Press any key to continue.8Задача №8*.
Пользователь вводит три дробных числа. Они интерпретируются, как коэффициенты a, b, c уравнения aх^2 + bx + c = 0. Необходимо вывести на экран решение данного уравнения.
Помните, что при отрицательном дискриминанте решений нет.
Хорошим решением будет, если программа не будет извлекать корень, когда корень не является целым числом, а просто выпишет, как и принято в математике, например, “sqrt(30)”.
Пример входных и выходных данных:
Пример чисел, которые ввёл пользователь:
1 2 -5Пример корректного вывода программы для вышенаписанных входных данных:
Your equation is: (1.000000)x^2 + (2.000000)x + (-5.000000) = 0
The solution is (-2.000000 + sqrt(24.000000)) / 2.000000 and (-2.000000 - sqrt(24.000000)) / 2.000000Решение:
Для достижения наилучшего результата и доступа ко всему курсу необходимо приобрести курс еженедельных индивидуальных или групповых занятий с преподавателем в режиме онлайн. Наши преподаватели обучат Вас создавать уникальные алгоритмы и самостоятельно реализовывать их в программном коде с соблюдением стандартов оформления.
Для записи на бесплатный пробный урок просто заполните форму ниже:
Целая часть числа – это часть, которая находится до запятой. То есть нужно только отбросить знаки после запятой или округлить число в меньшую сторону.
1) [2,73].
Округляем число 2,73 в меньшую сторону и получаем 2.
ОТВЕТ: [2,73] = 2.
2) [-8,04].
Для отрицательных чисел операция выделения целой части может показаться необычной. Кажется, что целая часть числа – 8,04 – это – 8, но на самом деле – 8 больше, чем – 8,04, а нам нужно округлить в меньшую сторону, поэтому правильным ответом будет – 9.
ОТВЕТ: [-8,04] = – 9.
3) [√5].
Извлечь корень из пяти мы не можем без помощи калькулятора, но можем найти √4 и √9. Это 2 и 3. Значит √5 – это число между двойкой и тройкой, значит его целая часть равна 2.
ОТВЕТ: [√5] = 2.
4) [-2п].
П только выглядит буквой, но за ней стоит число, приближенно равное 3,14. Поэтому целая часть числа (-2 * 3,14), то есть (- 6,28) будет равна -7.
ОТВЕТ: [-2п] = -7.
Как получить целую часть
Согласно определению, целой частью какого-либо числа называют наибольшее целое число, которое либо меньше, либо равно исходному. Получить целую часть можно разными способами – конкретный выбор зависит от того, какие инструменты по условиям задачи вы можете использовать (какой-либо язык программирования, табличный редактор, калькулятор, собственные математические способности и т.д.).

Инструкция
Разделите без остатка числитель на знаменатель, если требуется посчитать целую часть положительной обыкновенной дроби. Например, целой частью дроби 320/157 будет число 2. Если обыкновенная дробь является правильной (то есть, число в числителе больше числа в знаменателе), то и делить ничего не потребуется – целой частью будет ноль.
Проделайте все как это описано на предыдущем шаге, а затем уменьшите число на единицу, если требуется посчитать целую часть отрицательной обыкновенной дроби. Например, целой частью дроби -320/157 будет число -3. Эта особенность вытекает из определения – целая часть не может быть больше исходного числа.
Если обыкновенная дробь записана в смешанной форме, то и вычислять ничего не требуется – целая часть пишется перед дробной. Например, целой частью смешанной дроби 2 6/157 является число 2, а целая часть отрицательной смешанной дроби -2 6/157 равна -3.
Отбросьте дробную часть, если нужно найти целую часть от положительной десятичной дроби. Например, целая часть числа 3,14 равна 3. Для отрицательной десятичной дроби по-прежнему действуют правила, вытекающие из определения целой части – например, целая часть числа -3,14 равна -4.
Используйте функции округления в меньшую сторону, если получить целую часть числа надо с помощью какого-либо языка программирования. На языке PHP для этой операции предназначена функция floor() – например, floor(3.14). Точно так же она пишется и на языке СИ. На языке JavaScript синтаксис написания этой функции немного отличается – Math.floor(3.14).
Применяйте функцию ОКРУГЛВНИЗ(), если получить целую часть числа нужно средствами табличного редактора Microsoft Offict Excel.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.






















![{displaystyle [x]=sum _{n=-infty }^{+infty }nleft(theta (x-n)-theta (x-n-1)right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7423f699ff09217f72ad7593afe4cad2a8b99a4)
















