Центр масс кольца как найти

Центр масс

Это некоторое положение, определяемое относительно объекта или системы объектов. Это среднее положение всех частей системы, взвешенное в соответствии с их массами.

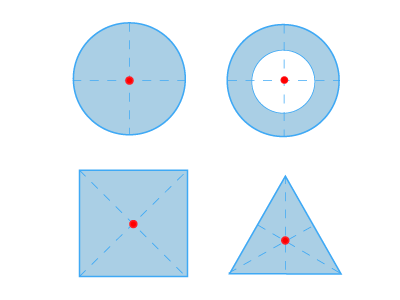
Для простых жестких объектов с равномерной плотностью центр масс находится в центре тяжести. Например, центр масс однородной формы диска будет в его центре. Иногда центр масс не находится в объекте. Например, центр масс кольца находится в его центре, где нет материала самого кольца.

Рисунок 1. Центр масс для некоторых простых геометрических фигур (обозначен красными точками).

Для более сложных фигур нужно более общее математическое определение:

Центр масс

Это уникальная позиция, в которой взвешенные векторы позиций всех частей системы суммируются до нуля.

Что полезного в центре масс?

Интересная вещь о центре масс объекта или системы состоит в том, что это точка, где действует любая однородная сила на объект. Это очень важно, потому что понимание этого облегчает решение механических задач, в которых мы должны описывать движение объектов разной формы и сложных систем.

Для расчетов мы можем рассматривать объект необычной формы, как если бы вся его масса была сосредоточена в крошечном объекте, расположенном в центре масс. Мы иногда называем этот воображаемый объект точечной массой.

Если мы нажимаем на твердый объект в его центре масс, то объект всегда будет двигаться, как будто это точечная масса. Он не будет вращаться вокруг любой оси, независимо от его фактической формы. Если объект подвергается неуравновешенной силе в какой-то другой точке, он начнет вращаться вокруг центра масс.

Как можно найти центр масс любого объекта или системы?

В общем, центр масс может быть найден путем сложения взвешенных векторов положения, которые указывают на центр масс каждого объекта в системе. Один из быстрых методов, который позволяет избежать использования векторной арифметики является нахождение центра масс отдельно для компонентов вдоль каждой оси. То есть:

Для положений объекта вдоль оси x:

ЦМx  =m1x1+m2x2+m3x3  m1+m2+m3ЦМ_x;=frac{m_1x_1+m_2x_2+m_3x_3;}{m_1+m_2+m_3}

И аналогично для оси у:

ЦМy  =m1y1+m2y2+m3y3  m1+m2+m3ЦМ_y;=frac{m_1y_1+m_2y_2+m_3y_3;}{m_1+m_2+m_3}

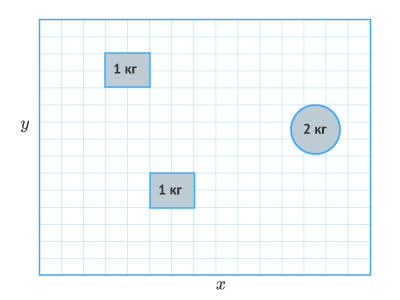
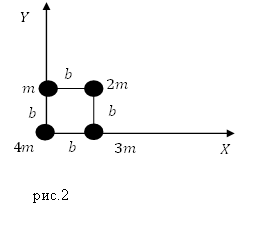
Вместе они дают полные координаты (Цм_x, Цм_y) центра масс системы. Например, рассмотрим систему из трех плоских объектов одинаковой плотности, показанную на рисунке 2.

Рисунок 2. Система из трех плоских объектов.

Расположение центра масс по оси х:

1⋅4+1⋅6+2⋅12  1+1+2=8,5frac{1cdot4+1cdot6+2cdot12;}{1+1+2}=8,5

и по оси y:

1⋅5+1⋅12+2⋅8,5  1+1+2=8,5frac{1cdot5+1cdot12+2cdot8,5;}{1+1+2}=8,5

Сложные объекты часто могут быть представлены в виде наборов простых форм, каждый из которых имеет одинаковую массу. Затем мы можем представить форму каждого компонента в виде точечной массы, расположенной в центре тяжести. Пустоты внутри объектов можно даже объяснить, представив их в виде фигур с отрицательной массой.

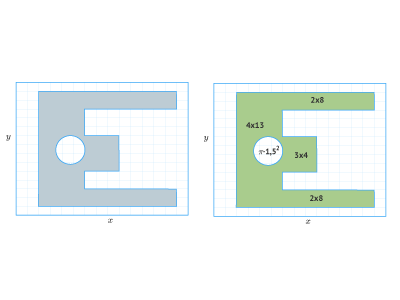
Рассмотрим плоский объект неправильной формы с равномерной плотностью, показанный на рисунке 3.

Рисунок 3. Плоский объект неправильной формы. Объект делится на простые формы.

Мы можем разбить этот сложный объект на четыре прямоугольника и один круг, как показано на рисунке справа. Здесь нас интересует только положение центра масс в относительных единицах, показанных на рисунке. Материал имеет однородную плотность, поэтому масса пропорциональна площади. Для простоты мы можем представить массу каждого сечения в единицах «квадратов», как показано на диаграмме.

По х оси, центр масс находится в:

16⋅10+52⋅4+12⋅7,5+16⋅10+(−7,1)⋅4,5  16+52+12+16−7,1=6,6frac{16cdot10+52cdot4+12cdot7,5+16cdot10+(-7,1)cdot4,5;}{16+52+12+16-7,1}=6,6

Важно, что площадь круговой пустоты π⋅1,52π·1,52 ∼7,1sim7,1 учитывается как отрицательная масса.

По y оси, центр масс находится в:

16⋅13+52⋅7,5+12⋅7,0+16⋅2+(−7,1)⋅7,5  16+52+12+16−7,1=7,4frac{16cdot13+52cdot7,5+12cdot7,0+16cdot2+(-7,1)cdot7,5;}{16+52+12+16-7,1}=7,4

Продолжение статьи читайте здесь.

Тест по теме «Центр масс»

Have you ever seen one of those toy birds that is able to balance on your fingertip by its beak without tipping over, as if by magic? It isn’t magic that allows the bird to balance at all, but the simple physics associated with center of mass.

Understanding the physics behind the center of mass allows you not only to understand conservation of momentum and other related physics, but can also inform stability and dynamics in the sports you play, as well as allow you to perform some creative balancing acts.

Definition of Center of Mass

An object’s ​center of mass​, sometimes also called the center of gravity, can be thought of as the point where the total mass of an object or a system can be treated as a point mass. In certain situations, external forces can be treated as though they are acting on the center of mass of the object.

For the toy bird balancing on your fingertip, the center of mass is at its beak. This might seem wrong at first, which is why the act of balancing appears magical. Indeed, for a bird sitting on a branch, its center of mass is somewhere in its body. But the balancing bird toy often has weighted wings that span outward and forward, causing it to balance differently.

The center of mass can be determined for a single object – such as the balancing bird – or it can be computed for a system of several objects, as you will see in a later section.

Center of Mass for a Single Object

There will always be a single point on a rigid body that is the location of that body’s center of mass. The position of the center of mass of an object depends on the distribution of mass.

If an object is of uniform density, its center of mass is easier to determine. For example, in a circle of uniform density, the center of mass is the center of the circle. (This would not be the case, however, if the circle was denser on one side than the other).

In fact, the center of mass will always be at the geometric center of the object when density is uniform. (This geometric center is called the ​centroid​.)

If the density is not uniform, there are other ways to determine the center of mass. Some of these methods involve the use of calculus, which is beyond the scope of this article. But one simple way to determine the center of mass of a rigid object is to simply try to balance it on your fingertip. The center of mass will be at the balancing point.

Another method, useful for planar objects, is as follows:

For some objects, however, it is possible for the balance point to be outside the bounds of the object itself. Think of a ring, for example. The center of mass for a ring shape is in the center, where no part of the ring exists at all.

Center of Mass of a System of Particles

The position of the center of mass for a system of particles can be thought of as their average mass position.

The same idea can be used as for a rigid object if you imagine this system of particles are all connected by rigid, massless plane. The center of mass would then be the balance point of that system.

To determine the center of mass of a system of particles mathematically, the following simple formula can be used:

vec{r} = frac{1}{M}(m_1vec{r_1} + m_2vec{r_2} + …

Where ​M​ is the total mass of the system, ​m_i​ are the individual masses and ​r_i​ are their position vectors.

In one dimension (for masses distributed along a straight line) you can replace ​r​ with ​x​.

In two dimensions, you can find the ​x​-coordinate and ​y​-coordinate of the center of mass separately as:

x_{cm} = frac{1}{M}(m_1x_1 + m_2x_2 + … \ text{ }\ y_{cm} = frac{1}{M}(m_1y_1 + m_2y_2 + …

Examples of Calculating the Center of Mass

​Example 1:​ Find the coordinates of the center of mass of the following system of particles: particle of mass 0.1 kg located at (1, 2), particle of mass 0.05 kg located at (2, 4) and particle of mass 0.075 kg located at (2, 1).

​Solution 1:​ Apply the formula for the ​x​-coordinate of the center of mass as follows:

x_{cm} = frac{1}{M}(m_1x_1 + m_2x_2 + m_3x_3) \text{ }\= frac{1}{0.1 + 0.05 + 0.075}(0.1(1) + 0.05(2) + 0.075(2))\text{ }\=0.079

Then apply the formula for the ​y​-coordinate of the center of mass as follows:

y_{cm} = frac{1}{M}(m_1y_1 + m_2y_2 + m_3y_3) \text{ }\= frac{1}{0.1 + 0.05 + 0.075}(0.1(2) + 0.05(4) + 0.075(1))\text{ }\=2.11

So the location of the center of mass is (0.079, 2.11).

​Example 2:​ Find the location of the center of mass of a uniform density equilateral triangle whose vertices lie at points (0, 0), (1, 0) and (1/2, √3/2).

​Solution 2:​ You need to find the geometric center of this equilateral triangle with side length 1. The ​x​-coordinate of the geometric center is straightforward – it is simply 1/2.

The ​y​-coordinate is a little trickier. It will occur at the location that a line from the top of the triangle to the point (0, 1/2) intersects with a line from any of the other vertices to the midpoint of one of the opposite side. If you sketch such an arrangement, you will find yourself with a 30-60-90 right triangle whose long leg is 0.5 and short leg is the ​y​-coordinate. The relationship between these sides is √3y = 1/2, hence y = √3/6, and the coordinates of the center of mass are (1/2, √3/6).

Motion of the Center of Mass

The location of the center of mass of an object or system of objects can be used as a reference point in many physics calculations.

When working with a system of interacting particles, for example, finding the center of mass of the system allows for an understanding of linear momentum. When linear momentum is conserved, the center of mass of the system will move with a constant velocity even as the objects themselves bounce off one another.

For a falling rigid object, gravity can be treated as acting on that object’s center of mass, even if that object is rotating.

The same is true of projectiles. Imagine tossing a hammer, and as it flies through an arc in the air, it rotates end over end. This might seem like complex motion to model at first, but it turns out that the center of mass of the hammer moves in a nice smooth parabolic path.

A simple experiment can be performed which demonstrates this by taping a small piece of glow tape to the hammer’s center of mass, and then tossing the hammer as described in a dark room. The glow tape will appear to move in a smooth arc, like a tossed ball.

A Simple Experiment: Find the Center of Mass of a Broom

A fun center-of-mass experiment that you can perform at home involves using a simple technique for finding the center of mass of a broom. All you need for this experiment is one broom and two hands.

With your hands relatively far apart, hold up the broom on the end of two pointer fingers. Then, slowly bring your hands closer together, sliding them underneath the broom. As you move your hands closer together you may notice one hand wants to slide along the underside of the broom handle while the other one stays put for a while before sliding.

The entire time your hands move, the broom remains balanced. Eventually, when your two hands meet, they will meet at the location of the broom’s center of mass.

Center of Mass of the Human Body

The center of mass of the human body is located somewhere near the navel (belly button). In men, the center of mass tends to be a little higher since they carry more body mass in their upper body, and in women, the center of mass is lower because they carry more mass in their hips.

If you stand on one foot, your center of mass will shift toward the side of the foot you are standing on. You may notice yourself leaning more toward that side. This is because in order to stay balanced, your center of mass needs to stay over the foot you are balancing on, or else you will tip over.

If you stand with one leg and hip against a wall and try to lift your other leg, you will likely find it impossible because the wall prevents your weight from shifting over the balance leg.

Another thing to try is standing with your back to the wall and your heels touching the wall. Then try to bend forward and touch the floor without bending your legs. Women may be more successful at this task than men because their center of mass is lower in their body and may end up still being over their toes as they lean forward.

Center of Mass and Stability

The location of the center of mass relative to an object’s base determines its stability. Something is considered stably balanced if, when tipped slightly and then released, it then returns back to its original position instead of tipping further and falling over.

Consider a three-dimensional pyramid shape. If balanced on its base, it is stable. If you lift one end slightly and let it go, it falls back down. But if you try to balance the pyramid on its tip, then any deviations from perfect balance will cause it to fall over.

You can determine if an object will fall back to its original position or tip over by looking at the location of the center of mass relative to the base. Once the center of mass moves past the base, the object will tip over.

If you play sports, you might be familiar with the ready position where you stand with a wide stance and knees bent. This keeps your center of mass low, and the wide base makes you more stable. Consider how hard someone would have to push you to tip you over if you are in the ready position vs. when you are standing up straight with your feet together.

Some cars have problems with rolling over when they take sharp turns. This is because of the location of their center of mass. If the center of mass of a vehicle is too high and the base is not wide enough, then it doesn’t take much to cause it to tip over. It’s always best for the stability of a vehicle to have most of the weight as low as possible.

Определение центра масс

При исследовании поведения систем частиц, часто удобно использовать для описания движения такую точку, которая характеризует положение и движение рассматриваемой системы как единого целого. Такой точкой служит центр масс.

Для однородных тел обладающих симметрией центр масс часто совпадает с геометрическим центром тела. В однородном изотропном теле одной выделенной точке найдется симметричная ей точка.

Радиус-вектор и координаты центра масс

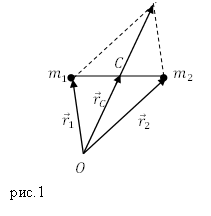
Предположим, что у нас имеются две частицы с равными массами, им соответствуют радиус-векторы: $<overline>_1 и <overline>_2$ . В этом случае центр масс расположен посередине между частицами. Центр масс (точка C) определён радиус-вектором $<overline>_C$ (рис.1).

Из рис.1 видно, что:

Можно ожидать, что вместе с геометрическим центром системы радиус-вектор, которого равен $<overline>_C,$ играет роль точка, положение которой определяет распределение массы. Ее определяют так, чтобы вклад каждой частицы был пропорционален ее массе:

Радиус -вектор $<overline>_C$, определенный выражением (2) – средне взвешенная величина радиус-векторов частиц $<overline>_1$ и $<overline>_2$. Это становится очевидным, если формулу (2) представить в виде:

Выражение (3) показывает, что радиус-вектор каждой частицы входит в $<overline>_C$ с весом, который пропорционален его массе.

Выражение (3) легко обобщается для множества материальных точек, которые расположены произвольным образом.

Если положения N материальных точек системы задано при помощи их радиус-векторов, то радиус – вектор, определяющий положение центра масс находим как:

Выражение (4) считают определением центра масс системы.

При этом абсцисса центра масс равна:

Ордината ($y_c$) центра масс и его аппликата ($z_c$):

Формулы (4-7) совпадают с формулами, которые используют для определения тяжести тела. В том случае, если размеры тела малы в сравнении с расстоянием до центра Земли, центр тяжести считают совпадающим с центром масс тела. В большинстве задач центр тяжести совпадает с центром масс тела.

Скорость центра масс

Выражение для скорости центра масс ($<overline>_c=frac>_c>

$) запишем как:

где $overline

$ – суммарный импульс системы частиц; $M$ масса системы. Выражение (8) справедливо при движениях со скоростями которые существенно меньше скорости света.

Если система частиц является замкнутой, то сумма импульсов ее частей не изменяется. Следовательно, скорость центра масс при этом величина постоянная. Говорят, что центр масс замкнутой системы перемещается по инерции, то есть прямолинейно и равномерно, и это движение не зависимо от движения составных частей системы. В замкнутой системе могут действовать внутренние силы, в результате их действия части системы могут иметь ускорения. Но это не оказывает влияния на движение центра масс. Под действием внутренних сил скорость центра масс не изменяется.

Примеры задач на определение центра масс

Задание. Система составлена из материальных точек (рис.2), запишите координаты ее центра масс?

Решение. Рассмотрим рис.2. Центр масс системы лежит на плоскости, значит, у него две координаты ($x_c,y_c$). Найдем их используя формулы:

Вычислим массу рассматриваемой системы точек:

Тогда абсцисса центра масс $x_ $равна:

Ответ. $x_c=0,5 b$; $y_с=0,3 b$

Задание. Космонавт, имеющий массу $m$, неподвижен относительно корабля массы $M$. Двигатель космического аппарата выключен. Человек начинает подтягиваться к кораблю при помощи легкого троса. Какое расстояние пройдет космонавт ($s_1$), какое корабль ($s_2$) до точки встречи? В начальный момент расстояние между ними равно $s$.

Решение. Центр масс корабля и космонавта лежит на прямой, соединяющей эти объекты.

В космосе, где внешние силы отсутствуют, центр масс замкнутой системы (корабль-космонавт) либо покоится, либо движется с постоянной скоростью. В избранной нами (инерциальной) системе отсчета он покоится. При этом:

Определения и формулы для вычисления центров тяжести

Определения и формулы для вычисления центров тяжести

• Чтобы ввести понятие центроида, разделите рассматриваемый объект на достаточно большое количество мелких объектов по сравнению с объектом или базовой частью любой формы. Гравитация элементарных частиц с индексом I, обусловленная действием Земли, обозначается DR, -, а гравитация всего объекта — R. Гравитация элементарных частиц объекта практически направлена ​​к центру Земли. Другими словами, это формирует систему конвергенции.

Давайте выясним, какие кривые C соединяют эти две точки, чтобы тяжелая материальная точка начиналась из точки A без начальной скорости. Людмила Фирмаль

Если размеры рассматриваемого объекта малы по сравнению с размером земного шара, гравитация элементарных частиц объекта может рассматриваться как система параллельных сил, направленных в одном направлении. Центр тяжести объекта является центром параллельной системы сил, образованной почти под действием силы тяжести его элементарных частиц. Радиус-вектор gf центра тяжести тела рассчитывается как радиус-вектор (рис. 88) центра параллельной силы по следующей формуле. £ г (DR, P Z Рисование Где r (радиус-вектор гравитационной точки действия базовой части тела, взятый за точку; DR — сила тяжести элементарных частиц; P = £ DR — сила тяжести всего тела.

Центр тяжести является точкой действия результирующей силы тяжести в случае силы тяжести. Отдельные его части считаются параллельными силовыми системами. Переходя к пределу в (1), увеличивая число основных частей n бесконечно, и получая DG (с производной dP, заменяя итоговое значение интегралом), г л-1 FDP P » » Где r — радиус-вектор основной части тела и принимается за точку. Для проекций на оси координат из (1) и (G): t X’p, МMLгg, д-р, Yn = ^ -p-, -7 = ^. fxdP _fTdP______fzdP We ’’ ’We

r’ zc’r ’ Где xc, усы и zc — координаты центра тяжести. x ^ yh z — координаты точки приложения силы тяжести для DR (. Используйте концепцию центроида тела, чтобы представить концепцию центроида.

Основная часть тела и гравитация всего тела могут быть выражены через массу At, M и ускорение свободного падения g, используя следующие уравнения: DR, = Am, г, P = Mg. Подставляя эти значения силы тяжести в (1) и (G) после уменьшения на g, которое предполагается одинаковым во всех частях тела, (2) В соответствии с этим (2 ‘) Уравнения (2) и (2 ‘) определяют радиус-вектор центра тяжести объекта. Центроид обычно определяется как радиус-вектор, который является геометрической точкой, независимой от центроида. Это рассчитывается по уравнению (2) или (2 ‘). В проекции на оси координат из (2) и (2 ‘) вы получите: £ X / дм, XY ^ m1 £ 2 , Где v — объем тела Присвойте эти значения (2) и (2 ‘). После уменьшения y „и p„, получите формулу соответственно.

После того как Ньютон сформулировал основные законы классической механики, их применение к несвободным твердым и механическим системам стало затруднительным до тех пор, пока не были сформулированы аксиомы связи. Людмила Фирмаль

Определить центр тяжести тела. Если тело имеет форму поверхности, то есть, если один из размеров меньше двух других, например тонкий лист железа, ДР,. = У5Д5 „P = ysS, где ys — удельный вес. D5; — площадь элементарных частиц на поверхности S — общая площадь поверхности. Получите следующее выражение: Для однородного тела, такого как провод, размер которого на два меньше по сравнению с третьим, можно определить радиус-вектор для центроида длины линии, используя следующую формулу: £ W fc = -! -. Где D / (длина элемента строки. Серьезность определяется. I — Общая длина линии, центр.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Центр масс. Определение. Формула. Центр тяжести.

Центр масс это геометрическая точка находящаяся внутри тела, которая определяет распределение массы этого тела. Любое тело можно представить в виде суммы некоторого количества материальных точек. В этом случае положение центра масс определяет радиус вектор.

mi – масса итой точки.

ri – радиус вектор итой точки.

Если просуммировать массы всех материальных точек, то получится масса всего тела. На положение центра масс влияет однородность распределения массы по объему тела. Центр масс может находиться как внутри тела, так и за его приделами. Скажем у кольца, центр масс находится в центре окружности. Там где нет вещества. В общем, для симметричных тел обладающих однородным распределением массы центр масс всегда находится в центре симметрии или на ее оси.

Если к телу прикладывать некоторую силу, то оно начнет двигаться. Представьте себе кольцо, лежащее на поверхности стола. Если к нему приложить силу, а попросту начать толкать, то оно будет скользить по поверхности стола. А вот направление движения будет завесить от места приложения силы.

Если силу направить от внешнего края к центру, по перпендикуляру к внешней поверхности, то кольцо начнет прямолинейно двигаться по поверхности стола в направлении приложения силы. Если же силу приложить по касательной к внешнему радиусу кольца, то оно начнет поворачиваться относительно своего центра масс. Таким образом, можно заключить, что движение тела состоит из суммы поступательного движения и вращательного относительно центра масс. То есть движение любого тела можно описать движением материальной точки находящейся в центре масс и имеющей массу всего тела.

Существует также понятие центр тяжести. В общем, это не одно и то же что и центр масс. Центр тяжести это точка относительно, которой общий момент силы тяжести равен нулю. Если представить себе стержень длинной скажем 1 метр, диаметром 1см, и однородный по своему сечению. На концах стержня закреплены металлические шары одинаковой массы. То центр масс этого стержня будет находиться посередине. Если этот стержень поместить в неоднородное гравитационное поле, то центр тяжести будет смещён в сторону большей напряжённости поля.

На поверхности земли, где сила тяжести однородна, центр масс практически совпадает с центром тяжести. Для любого постоянного однородного гравитационного поля центр тяжести всегда будет совпадать с центром масс.

[spoiler title=”источники:”]

http://lfirmal.com/opredeleniya-i-formuly-dlya-vychisleniya-centrov-tyazhesti/

Центр масс. Определение. Формула. Центр тяжести

[/spoiler]

2017-01-15   

Где находится центр масс однородного проволочного полукольца?

Решение:

Заменим полукольцо половиной вписанного в окружность радиусом $R$ правильного многоугольника $ABCD cdots$, сделанного из той же проволоки, и найдем момент сил тяжести, приложенных к звеньям многоугольника, относительно вертикальной оси ОА — оси х (рис.):

$M = rho lg(P_{1}O_{1} + P_{2}O_{2} + cdots)$.

Здесь $rho$ — линейная плотность проволоки, $l$ — длина одного звена, $P_{1}O_{1}, P_{2}O_{2} cdots$ — расстояния от оси до середины звеньев.

Заметим теперь, что треугольники $AB^{ prime}B$ и $O_{1}P_{1}O$ подобны. Следовательно,

$frac{AB^{ prime}}{AB} = frac{P_{1}O_{1}}{OO_{1}}$ или $l cdot P_{1}O_{1} = AB^{ prime} cdot OO_{1}$.

Аналогично, из подобия треугольников $BQC$ и $OP_{2}O_{2}$ получаем: $l cdot P_{2}O_{2} = B^{ prime}C^{ prime} cdot OO_{2}$.

Обозначив $OO_{1} = OO_{2} = cdots = h$, имеем:

$M = rho hg (AB^{ prime} + B^{ prime}C^{ prime} + cdots)$.

Выражение в скобках дает удвоенный радиус (диаметр) окружности: $M = 2R rho hg$. Если число звеньев вписанного многоугольника устремить к бесконечности, величина $h$ будет стремиться к радиусу окружности $R$, а момент к $2R^{2} rho g$. С другой стороны, момент равен произведению силы тяжести проволоки $|pi R rho g$ на расстояние $y_{c}$ от центра тяжести до оси ОА. Таким образом

$2R^{2} rho g = pi R rho g y_{c}$,

откуда $y_{c} = 2R/ pi$.

Ответ: в системе координат с началом в центре полукольца, когда положительная полуось $y$ содержит все $y$-координаты его точек, координаты центра масс: $x_{c} = 0, y_{x} = 2R/ pi$.