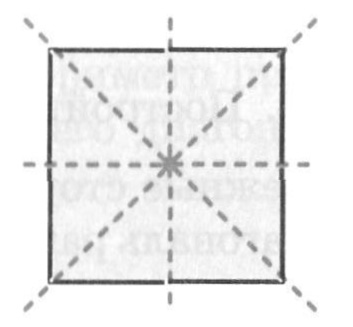
Какая симметрия есть у параллелограмма?
Утверждение
Параллелограмм — центрально-симметричная фигура.
Центром симметрии параллелограмма является точка пересечения его диагоналей.
Доказательство:
 Пусть X — произвольная точка параллелограмма. Проведём луч XO. На пересечении XO со стороной CD отметим точку X1. Рассмотрим треугольники XOB и X1OD:
Пусть X — произвольная точка параллелограмма. Проведём луч XO. На пересечении XO со стороной CD отметим точку X1. Рассмотрим треугольники XOB и X1OD:
1) BO=OD (по свойству диагоналей параллелограмма)
2) ∠BOX=∠DOX1 (как вертикальные)
3) ∠XBO=∠X1DO (как внутренние накрест лежащие при AB ∥ CD и секущей BD).
Следовательно, треугольники XOB и X1OD равны (по стороне и двум прилежащим к ней углам).
Из равенства треугольников следует равенство соответствующих сторон: XO=X1O, то есть точки X и X1 симметричны относительно точки O.
Имеем: точка, симметричная произвольной точке параллелограмма, также принадлежит параллелограмму. Следовательно, параллелограмм является централь-симметричной фигурой.
Что и требовалось доказать.
В общем виде параллелограмм осей симметрии не имеет. Осевой симметрией обладают только его частные случаи — прямоугольник, ромб и квадрат.
Осевая и центральная симметрия

О чем эта статья:
Что такое симметрия
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.
Центр симметрии — это точка, в которой пересекаются все оси симметрии.
Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.
Рассмотрите фигуры с осевой и центральной симметрией.
- Ось симметрии угла — биссектриса.
- Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
- Оси симметрии прямоугольника проходят через середины его сторон.
- У ромба две оси симметрии — прямые, содержащие его диагонали.
- У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
- Ось симметрии окружности — любая прямая, проведенная через ее центр.
Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.
Осевая симметрия
Вот как звучит определение осевой симметрии:
Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.
При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.
Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.
В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.
Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.
Пример 1. Постройте треугольник A1B1C1 ,симметричный треугольнику ABC относительно прямой.
- Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
- Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
- С другой стороны прямой отложим такие же расстояния.
- Соединяем точки отрезками и строим треугольник A1B1C1, симметричный треугольнику ABC.
- Получаем два треугольника, симметричных относительно оси симметрии.
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.
- Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
- Измеряем расстояние от вершин до точек на прямой.
- Откладываем такие же расстояния на другой стороне оси симметрии.
- Соединяем точки и строим треугольник A1B1C1.
Пример 3. Построить отрезок A1B1, симметричный отрезку AB относительно прямой l.

- Проводим через точку А прямую, перпендикулярную прямой l.
- Проводим через точку В прямую, перпендикулярную прямой l.
- Измеряем расстояния от точек А и В до прямой l.
- Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A1 и B1.
- Соединяем точки A1 и B1.
Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!
Центральная симметрия
Теперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.
Пример 1: Постройте треугольник A1B1C1 ,симметричный треугольнику ABC, относительно центра (точки О).
- Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
- Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
- Получившиеся точки соединяем отрезками A1B1 A1C1 B1C1.
- Получаем треугольник A1B1C1, симметричный треугольнику ABC, относительно центра.
Пример 2. Построить отрезок A1B1, симметричный отрезку AB относительно центра (точки О).
- Измеряем расстояние от точки B до точки О и от точки А до точки О.
- Проводим прямую из точки А через точку О и выводим ее на другую сторону.
- Проводим прямую из точки B через точку О и выводим ее на другую сторону.
- Чертим на противоположной стороне отрезки А1О и B1О, равные отрезкам АО и АB.
- Соединяем точки A1 и B1 и получаем отрезок A1B1, симметричный данному.
Задачи на самопроверку
В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!
Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.
Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:
Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная
Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М1 и N1 — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М1N1.
Подсказка: опустите перпендикуляры из точек N и N1 на прямую MМ1.
Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.
Центральная симметрия
Центральная симметрия — это симметрия относительно точки.
Пусть дана некоторая точка O. Чтобы построить точку, симметричную относительно точки O некоторой точке A, надо:
1) Провести луч AO.
2) С другой стороны от точки O на луче AO отложить отрезок OA1, равный отрезку AO.
Полученная точка A1 симметрична точке A относительно точки O.
Точка O называется центром симметрии.
Таким образом, точки A и A1симметричны относительно точки O, если O — середина отрезка AA1. Точка O считается симметричной самой себе.
Преобразование фигуры F в фигуру F1, при котором каждая точка A фигуры F переходит в точку A1, симметричную относительно данной точки O, называется преобразованием симметрии относительно точки O. Фигуры F и F1 называются фигурами, симметричными относительно точки O.
Чтобы построить треугольник, симметричный треугольнику ABC относительно точки O, достаточно построить точки A1, B1 и C1, симметричные точкам A, B и C относительно точки O, и соединить их отрезками.
Треугольники ABC и A1B1C1 симметричны относительно точки O.
Если преобразование симметрии относительно точки O переводит фигуру в себя, то такая фигура называется центрально-симметричной, а точка O называется центром симметрии этой фигуры.
Примеры центрально-симметричных фигур:
1) Параллелограмм.
Центр симметрии параллелограмма — точка пересечения его диагоналей.
Центр симметрии окружности — её центр.
3) Прямая.
Центром симметрии прямой является любая точка этой прямой ( то есть прямая имеет бесконечное множество центров симметрии).
Преобразование симметрии относительно точки является движением.
Понятие осевой и центральной симметрии
Презентация к уроку
Цели и задачи:
- совершенствование знаний об осевой симметрии;
- познакомить с понятием центральная симметрия;
- научить распознавать фигуры, обладающие осевой симметрией и центральной симметрией;
- совершенствование знаний и умений при работе с чертежно – измерительными инструментами;
- развивать пространственное воображение, конструкторские навыки и творчество;
- способствовать развитию интереса к техническому творчеству;
- расширение кругозора.
Материалы и инструменты:
- Компьютер учителя (ноутбук), мультимедийный проектор, экран; слайдовая презентация к занятию; циркуль для доски; циркули ученические, треугольники, цветной картон и бумага, ножницы, клей.
– Организационная часть (подготовка к работе).
– Актуализация опорных знаний.
– Повторение геометрического материала.
– Практическая работа, объяснение и показ основных методов выполнения работы, соревнования.
– Подведение итогов занятия, обсуждение выполненной работы.
– Уборка рабочих мест.
Организационный момент. Проверка готовности к занятию.
Задание №1. “Разделите треугольник” Слайд 2

Разделите представленный на рисунке равносторонний треугольник следующим образом:
1. Тремя линиями на четыре равные части.
2. Тремя линиями на шесть равных частей.
3. Тремя линиями на три равные части.
4. Одной линией на четыре произвольные части
Задание №2. Слайд 3
В квадрате 6 на 6 клеток нарисовать геометрический орнамент, через 2 два столбика клеток его повторить до конца листа.
В древности слово “СИММЕТРИЯ” употреблялось в значении “гармония”, “красота”. Действительно, в переводе с греческого это слово означает “соразмерность, пропорциональность, одинаковость в расположении частей”.
С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого развития. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность. Что же такое симметрия? Почему симметрия буквально пронизывает весь окружающий нас мир?
Мы рассмотрим ту симметрию, которую можно непосредственно видеть – симметрию положений, форм, структур. Она может быть названа геометрической симметрией.
ОСЕВАЯ СИММЕТРИЯ Слайд 4
Равнобедренный (но не равносторонний) треугольник имеет также одну линию симметрии. А равносторонний треугольник – три линии симметрии.
У неразвёрнутого угла одна линия симметрии – прямая, на которой расположена биссектриса угла.
Прямоугольник и ромб, не являющиеся квадратами имеют по две линии симметрии, а квадрат – четыре линии симметрии.
Выступление “Зеркальная (осевая) симметрия” Приложение № 1
Найдите фигуры, обладающие линией симметрии (Задание №1) Приложение № 2
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ Слайд 8
Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.
Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма – точка пересечения его диагоналей.
Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии у прямой их бесконечно много – любая точка прямой является её центром симметрии.
Примером фигуры, не имеющей центра симметрии, является треугольник.
Найдите фигуры, обладающие центральной симметрией (Задание №2) Приложение № 2
Найдите фигуры, имеющие обе оси симметрии (Задание №3) Приложение № 2
Выступление “Симметрия в буквах” Приложение № 3
Раз – руки вверх махнули
И при том вздохнули
Два – три нагнулись, пол достали
А четыре – прямо встали и сначала повторяем.
Воздух сильно мы вдыхаем
При наклонах выдох дружный
Но колени гнуть не нужно.
Чтобы руки не устали,
Мы на пояс их поставим.
Прыгаем как мячики
Девочки и мальчики.
Практическая работа “Летающая тарелка” Приложение № 5
На какое геометрическое тело похожа летающая тарелка? (цилиндр)
Каким инструментом мы будем пользоваться? (циркуль)
Правила техники безопасности при работе с циркулем.
Сейчас начинаем практическую работу (рис.10):
- Для изготовления летающей тарелки используем картон любого цвета.
- На изнаночной стороне картона чертим окружность R55 (1 деталь) и R36 (2 детали).
- По длине картона откладываем прямоугольник длиной 220 мм и шириной 12 мм (по длине отмечаем клапаны).
- Вырезаем все детали.
- Склеиваем детали №2 и №3, получился цилиндр.
- Приклеиваем цилиндр на деталь №1
- Получилась “Летающая тарелка”.
- Оформление по собственному замыслу.
- Соревнования.
- Подведение итогов
Сегодня на занятии мы с вами повторили и изучили осевую и центральную симметрии.
- Сколько осей симметрии имеет отрезок, прямая? (по 2).
- Имеют ли центр симметрии отрезок, прямая, квадрат? (по2)
- Какие из данных букв имеют ось симметрии? (М, А, Н, Е)
- Какие из данных букв имеют центр симметрии? (Н, О) Приложение № 6
Сегодня все хорошо поработали и разобрались с симметрией, но если кто – то все-таки сомневается, я вам подготовила вот такую подсказку
Награждение и поздравление победителей соревнований.
Уборка рабочих мест.
Литература.
- Тарасов Л. Этот удивительный симметричный мир. М., 1982 г.
- Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. М., 1995 г.
- Интернет ресурсы.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/622273
[/spoiler]
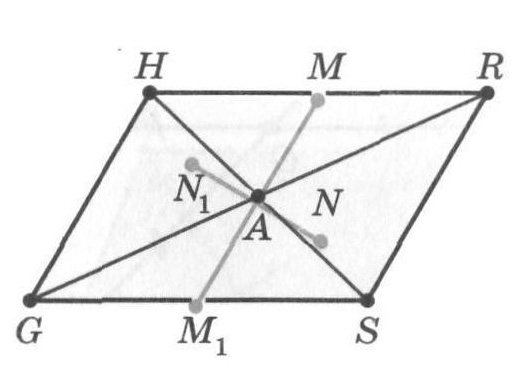
Теорема: Точка пересечения диагоналей параллелограмма является его центром симметрии.
Доказательство:
Пусть GR и HS — диагонали параллелограмма GHRS, пересекающиеся в точке А.
Пусть М — произвольная точка на границе параллелограмма, например на стороне HR. Найдем точку, симметричную точке М относительно точки А. Для этого проведем луч МА, который пересекает сторону GS в точке M1. Треугольники AMR и AM1G равны, так как у них равны углы MAR и M1AG, MRA и M1GA, а также стороны AR и AG.
Значит, АМ1 — AM. Это означает, что точки М и М1 равноудалены от точки А. Поэтому М1 — точка, центрально-симметричная точке М относительно точки А. Таким образом, для любой точки М на границе параллелограмма центрально-симметричная ей точка также лежит на границе параллелограмма. Теперь понятно, что если взять произвольную внутреннюю точку N параллелограмма GHRS, то точка N1, симметричная ей относительно точки А, также является внутренней точкой этого параллелограмма. Значит, точка А пересечения диагоналей параллелограмма GHRS является его центром симметрии.
Поскольку параллелограмм — центрально-симметричная фигура, то и его виды — прямоугольник и ромб, а значит, и вид ромба — квадрат являются центрально симметричными фигурами.
Оси симметрии и центы симметрии плоских фигур
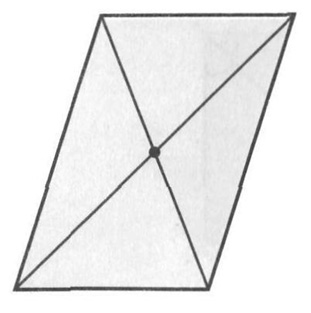
Таким образом, параллелограмм имеет центр симметрии:
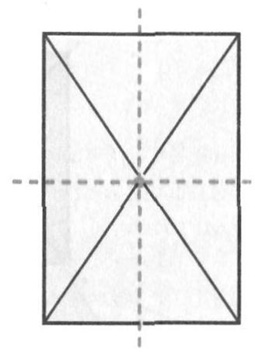
Прямоугольник имеет центр симметрии и две оси симметрии:
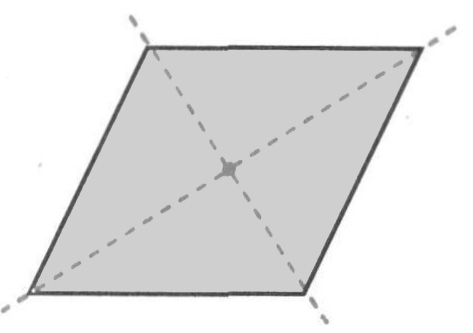
Ромб имеет центр симметрии и две оси симметрии:
Квадрат имеет центр симметрии и четыре оси симметрии:
Теперь вы знаете разные виды четырехугольников и основные их свойства и признаки.
в параллелограмме ABCD A(-3; 4) С(9; -2). Найдите координаты центра симметрии параллелограмма
Светило науки – 68 ответов – 0 раз оказано помощи
Центр симметрии это точка пересечения диагоналей, а точка пересечения диагоналей делит их пополам ⇒ надо найти координату середины диагонали AC(т.к нам даны координаты A и C)
Вычислим по формуле:
((x₁+x₂)/2;(y₁+y₂)/2),где A(x1; y1) и C(x2; y2)
(6/2;2/2)
(3;1)
Отв:(3;1)

Светило науки – 9 ответов – 0 раз оказано помощи
x=(x1+x2)/2=(-3+9)/2=3
y=(y1+y2)2=(4-2)/2=2
точка=(3$2)
<< Назад | Оглавление | Далее >>
4.4. Симметрия относительно точки. Параллелограмм
Немного терминологии
Пусть нам даны на плоскости две произвольные прямые m и n. Отметим на прямой m какую-либо точку M, а на прямой n — какую-либо точку N. Проведем третью прямую через точки M и N. При этом образуется две четверки углов, как показано на рисунке:
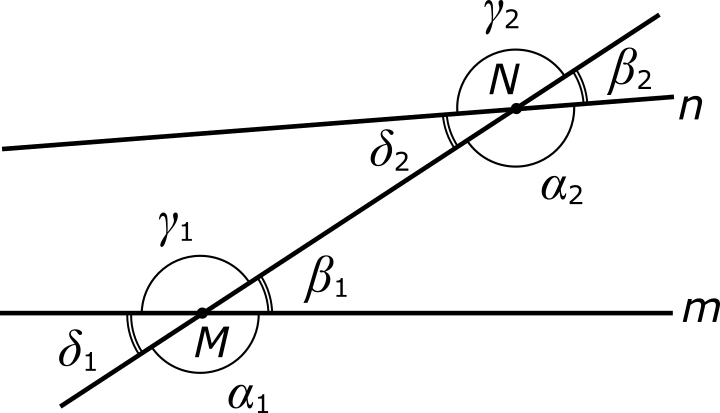
Здесь у дуг, обозначающих углы, отсутствуют стрелочки, поскольку нас сейчас интересуют угловые расстояния, а не угловые смещения. Можно сказать, что в данной геометрической конструкции угол α1 соответствует углу α2. Именно так эти углы и называются — соответственными по отношению друг к другу. Аналогичным образом, соответственными являются пары углов:
β1 и β2,
γ1 и γ2,
δ1 и δ2.
(Замечу в скобках, что похожие по смыслу величины у математиков принято обозначать одинаковыми буквами и различать их по так называемому индексу — числовому или буквенному довеску, приписываемому справа внизу мелким шрифтом. Так, в обозначении α1 основным символом является α, а индексом — число 1.)
На прошлом уроке мы ввели понятие параллельных прямых: две несовпадающие прямые называются параллельными, если угол между ними равен нулю.
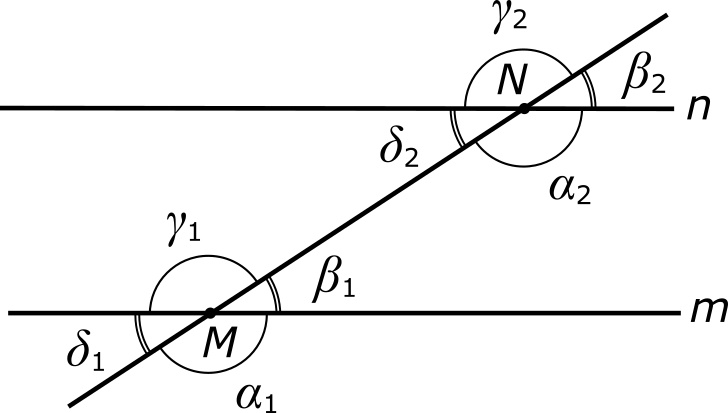
Угол же между двумя прямыми всегда можно найти как разность соответственных углов, образуемых при пересечении с какой-либо третьей прямой. Так, угол φ между прямыми m и n равен
φ = |α2 − α1|.
Здесь мы взяли результат по абсолютной величине, поскольку речь идет об угловом расстоянии, а не об угловом смещении. При этом совершенно безразлично, какую пару соответственных углов брать. С тем же успехом мы могли бы написать
φ = |β2 − β1|,
φ = |γ2 − γ1|,
φ = |δ2 − δ1|.
Действительно, угол β1 является смежным с углом α1, а угол β2 — смежным с углом α2, следовательно,
β1 = 180° − α1,
β2 = 180° − α2,
|β2 − β1| = |α2 − α1|.
По точно такой же причине,
|δ2 − δ1| = |α2 − α1|.
Что же касается углов γ1 и γ2, то они являются вертикальными по отношению к α1 и α2, а потому
γ1 = α1,
γ2 = α2,
Значит, угол φ между прямыми n и m можно найти как
φ = |α2 − γ1|.
Углы α2 и γ1 в рассматриваемой геометрической конструкции называются внутренними накрест лежащими. Другой парой внутренних накрест лежащих углов здесь являются углы δ2 и β1, разность которых также можно использовать для нахождения угла φ:
φ = |δ2 − β1|.
Таким образом, две прямые, пересеченные какой-либо третьей, являются параллельными тогда и только тогда, когда внутренние накрест лежащие углы равны между собой.
Симметрия относительно точки
Рассмотрим на плоскости две произвольные параллельные прямые m и n. Пусть M — какая-либо точка, принадлежащая прямой m, а N — какая-либо точка, принадлежащая прямой n. Соединим эти точки отрезком MN. Выберем какую-либо пару накрест лежащих углов и обозначим каждый из них буквой α (мы вправе это сделать, потому что эти углы равны между собой).
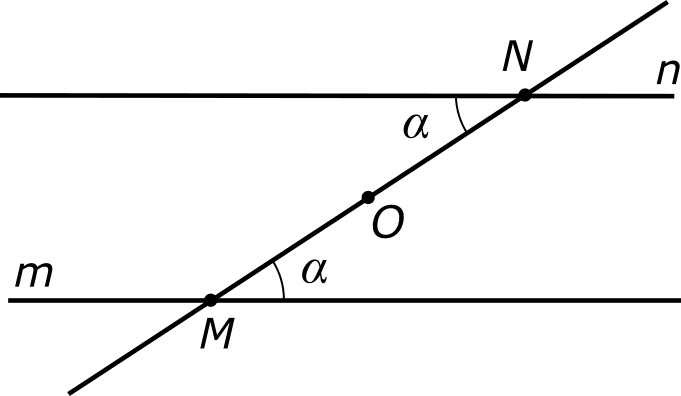
Отметим на отрезке MN середину и обозначим ее буквой O. В скором времени мы научимся изящному способу делить отрезок на любое число частей, но пока мы можем просто измерить длину отрезка MN (напомню, что она обозначается как |MN|), поделить ее пополам: |MN|/2, а потом отложить указанное расстояние вдоль отрезка MN, начиная от любого из его концов.
Теперь, не выходя из плоскости, повернем полученную геометрическую конструкцию на полоборота (180°) вокруг точки O. При этом, как это принято в математике, за старыми положениями точек M и N сохраняются старые обозначения, а для их новых положений мы должны подобрать новые обозначения, например, M1 и N1. Это же относится и к обозначениям прямых. Если до поворота они обозначались как m и n, то после поворота они должны обозначаться как-то по-другому, например, m1 и n1.
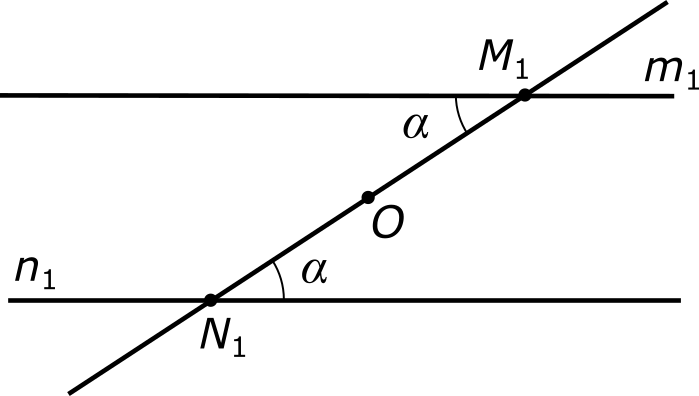
Примечание. Когда мы вводили понятие точки, мы отмечали, что, если не оговорено противное, точки считаются неподвижными. Теперь к этому необходимо добавить, что только неподвижные точки могут иметь собственные обозначения, такие как M, N, M1, N1 и т.п. Подвижная же точка собственного обозначения никогда не имеет и распознается по той неподвижной точке, где она в данный момент находится. Это же относится и, вообще, к любым подвижным геометрическим объектам (прямым, отрезкам и др.).
Нетрудно видеть, что местоположение точки N1 полностью совпадает с местоположением точки М, то есть фактически это одна и та же точка. Подобным же образом, точка М1 совпадает с точкой N. Более того, из-за равенства накрест лежащих углов прямая n1 в точности ложится на прямую m, а прямая m1 — на прямую n. Возвращаясь к первоначальным обозначениям, мы приходим к тому же самому положению вещей, которое было до поворота:

Мы рассмотрели частный случай так называемой симметрии относительно точки. В общем случае эта симметрия определяется следующим образом. Пусть на плоскости задана некоторая точка O. Симметрией относительно этой точки называется поворот вокруг нее на угол 180° (в пределах той же плоскости).
При этом сама точка O называется центром симметрии.
Точки М и N, переходящие друг в друга в результате такого поворота, называются симметричными (одна по отношению к другой). Центр симметрии O лежит на отрезке МN и делит его в точности пополам.
Также называются симметричными любые пары геометрических объектов (прямых, отрезков и т.п.), если они переходят друг в друга.
Про геометрическую конструкцию, которая переходит сама в себя, говорят, что она центрально-симметрична или же что она обладает центром симметрии (подразумевая под таким центром точку O).
Пусть даны две произвольные точки M и O. Чтобы построить точку N, симметричную точке M относительно центра O, надо проделать следующее.
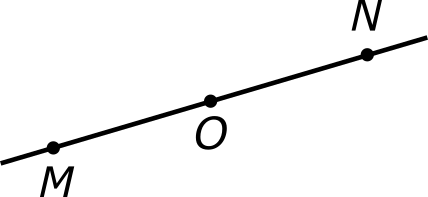
Проведем прямую OM. Направление от O к M примем за положительное. Отложим от точки O вдоль прямой в отрицательном направлении отрезок ON, равный по длине отрезку OM. Угол ∠MON равен по величине 180°, а значит, его стороны получаются друг из друга поворотом на 180° (безразлично в каком направлении), при этом точка M переходит в точку N, и наоборот, точка N переходит в точку M. Таким образом, эти точки являются симметричными.
Перечислим некоторые очевидные свойства симметрии относительно точки.
Прямая центрально-симметрична относительно любой из своих точек.
Отрезок центрально-симметричен относительно своей середины.
Если точки M и N симметричны, то центр симметрии O совпадает с серединой отрезка MN.
Параллельные прямые симметричны относительно середины отрезка, один из концов которого лежит на одной прямой, а другой конец — на другой прямой. (Мы это доказали чуть выше).
Параллелограмм
Вернемся к паре параллельных прямых m и n из предыдущего пункта. Отметим на прямой m произвольную точку K, не совпадающую с M, и проведем через точки K и N прямую, которую мы обозначим буквой k.
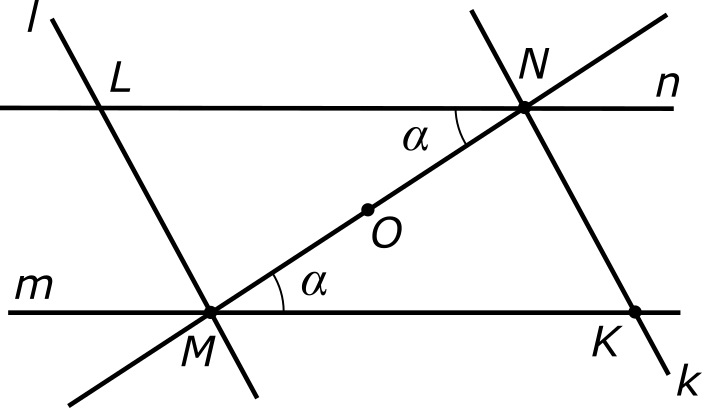
Далее, проведем через точку M еще одну прямую, параллельную k, и обозначим ее через l. Мы снова пришли к симметричной конструкции. Мы имеем:
Прямые m и n симметричны, как было показано ранее.
Прямые k и l симметричны по той же причине, что и прямые m и n.
Прямые k и m пересекаются в точке K.
Следовательно, у прямых l и n также есть точка пересечения, которая симметрична точке K. Обозначим ее буквой L.
У нас образовалась замкнутая цепочка из четырех отрезков LM, MK, KN и NL. В этой цепочки соседние отрезки имеют общие концы, а противоположные отрезки параллельны (то есть лежат на параллельных прямых). Внутренняя часть плоскости, ограниченная такой цепочкой, называется параллелограммом.
Отрезки, служащие границей, также принадлежат параллелограмму и называются его сторонами.
Концы сторон, где они соединяются друг с другом, называются вершинами параллелограмма.
Внутренние углы между соседними сторонами (при вершинах) называются углами параллелограмма.
Отрезки, соединяющие противоположные вершины параллелограмма, называются его диагоналями.
Всего у параллелограмма две диагонали, из которых мы пока построили только одну — отрезок MN. Проведем другую диагональ — KL. Она пересекает первую диагональ в точке O и делится этой точкой пополам (в силу симметричности конструкции).
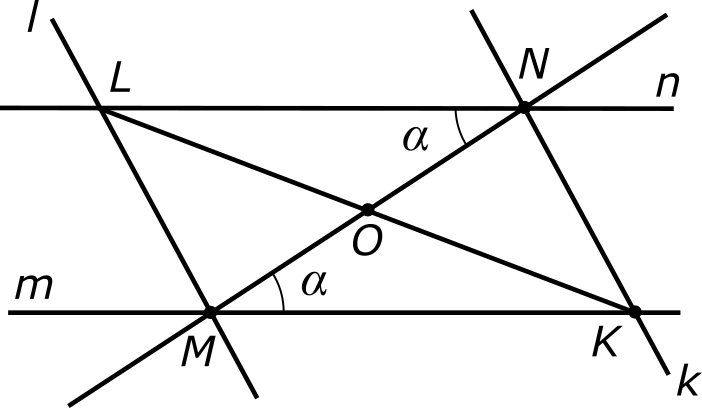
Таким образом, мы установили, что параллелограмм обладает центром симметрии, который находится в точке пересечения диагоналей. Вот еще два полезных свойства параллелограмма, следующие из его симметричности:
Длины противоположных сторон параллелограмма одинаковы.
Противоположные углы параллелограмма равны между собой.
Параллелограмм обычно обозначают, перечисляя его вершины. Параллелограмм, который мы построили в данном случае, можно обозначить как LMKN.
Конспект
Угол между двумя прямыми, пересеченными третьей прямой, может быть найден как разность соответственных углов или же как разность внутренних накрест лежащих углов. В обоих случаях разность следует брать по абсолютной величине.
Две прямые, пересеченные третьей, параллельны тогда и только тогда, когда соответственные углы равны между собой. Такое же утверждение справедливо и для внутренних накрест лежащих углов.
Симметрия относительно точки O: поворот вокруг этой точки на 180° (в пределах заданной плоскости).
Построение точки N, которая симметрична точке M относительно центра O: на прямой OM откладываем отрезок ON, равный по длине |OM|, в противоположную от M сторону.
Параллелограмм: внутренняя часть плоскости, ограниченная замкнутой цепочкой из четырех отрезков, в которой противоположные отрезки параллельны друг другу. Граница принадлежит параллелограмму.
У параллелограмма имеются: стороны (граничные отрезки), вершины (точки соединения сторон), углы (внутренние при вершинах), диагонали (отрезки, соединяющие противоположные вершины).
Свойства параллелограмма:
Центром симметрии является точка пересечения диагоналей.
Длины противоположных сторон одинаковы.
Противоположные углы равны между собой.