Центр выпуклого многоугольника как найти

В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как

,

где интегрирование выполняется по объёму тела. Другое название барицентра в этом значении — центроид.

Неформально, геометрический барицентр есть точка равновесия фигуры, вырезанной из картона, в предположении, что картон имеет постоянную плотность, а внешнее гравитационное поле однородно.

В физике термин «барицентр» — синоним понятия «центр масс», используемый, в основном, в задачах космической механики. Центр масс объекта является средним арифметическим всех его точек с учётом локальной плотности массы. Для физических объектов с постоянной плотностью центр масс совпадает с барицентром фигуры той же формы.

Ниже барицентр рассматривается в математическом (геометрическом) смысле, о барицентре в физике см. статью Центр масс.

Свойства[править | править код]

Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.

Если барицентр известен, он является фиксированной точкой группы изометрии симметрий фигуры. Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильного многоугольника, правильного многогранника, цилиндра, прямоугольника, ромба, окружности, сферы, эллипса, эллипсоида, суперэллипса, суперэллипсоида и т. д.) можно найти исходя исключительно из этого принципа.

В частности, барицентром треугольника является точка пересечения его медиан (см. рисунок). Барицентром параллелограмма является точка пересечения его диагоналей, но это неверно для других четырёхугольников.

Барицентр объекта с трансляционной симметрией не определён (или лежит вне пространства фигуры), поскольку сдвиг не имеет фиксированной точки.

Центроид треугольника[править | править код]

• Барицентр треугольника называется центроидом и лежит на пересечении трёх медиан, также лежит на прямой Эйлера (проходящей и через другие ключевые точки, включая ортоцентр и центр описанной окружности)^[1][2].

• Если в вершины треугольника поместить равные массы, то центр масс (барицентр) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой массой также находится в центроиде.

^[3].

• Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин треугольника:

^[3].

• Центр масс сторон треугольника совпадает с центром вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с инцентром дополнительного треугольника, или с центром Шпикера.
• О других свойствах центроида треугольника смотрите ниже.

Минимаксные свойства центроида треугольника[править | править код]

• Центроид или точка пресечения медиан треугольника является единственной точкой треугольника такой, что проведенные через неё три чевианы разделяют своими концами стороны треугольника на шесть отрезков. При этом произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально^[4].
• Центроид или точка пересечения трёх медиан является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).

Центроид четырёх точек (вершин четырёхугольника)[править | править код]

Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противолежащих сторон. Точка пересечения делит все три отрезка пополам.

Центр масс вершин четырёхугольника не обязан совпадать с центром масс самого четырёхугольника как плоской фигуры.

Определение местоположения барицентра[править | править код]

Определение местоположения барицентра однородной плоской фигуры методом отвеса[править | править код]

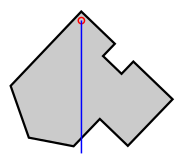
Барицентр однородной плоской фигуры, такой как фигура (a) на рисунке, можно найти экспериментально с использованием отвеса и булавки путём нахождения центра масс тонкой пластины однородной плотности, имеющей ту же форму. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке (b). Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр (c).

Этот метод можно распространить (в теории) на вогнутые фигуры, когда барицентр лежит вне их, а также тела (постоянной плотности), но положение линии отвеса придётся отмечать каким-то иным способом.

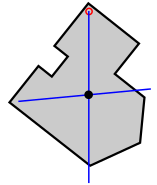
Определение местоположения барицентра выпуклой двумерной фигуры методом балансировки[править | править код]

Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например, на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.

Определение местоположения барицентра для конечного множества точек[править | править код]

Барицентр конечного множества из точек в находится по формуле

^[5].

Полученная точка такая, что сумма квадратов расстояний между ней и точками множества является минимальной.

Определение местоположения барицентра с помощью геометрического разложения[править | править код]

Барицентр плоской фигуры можно вычислить, разделив её на конечное число более простых фигур , найдя положение барицентров и площадей каждой части, а затем вычислив

Дыры в фигуре , наложения частей, или части, выступающие за фигуру, можно рассматривать как фигуры с отрицательной площадью . А именно, знак площади нужно выбирать так, чтобы сумма знаков для всех частей, включающих точку , была равна 1, если принадлежит , и 0 в противном случае.

Например, фигуру (a) на рисунке легко разделить на квадрат и треугольник с положительным знаком, круглое отверстие с отрицательным (b).

Барицентр каждой части легко найти в любом списке барицентров простых фигур (c). Затем вычисляется барицентр фигуры, как средневзвешенное трёх точек. Горизонтальное положение барицентра, считая от левого края фигуры, равно

Вертикальное положение вычисляется аналогично.

Та же формула применима для любого трёхмерного объекта, только обозначают уже объёмы частей тела , а не площади. Формула верна также для пространства любой размерности при замене площади -мерными мерами частей.

Определение местоположения барицентра интегрированием[править | править код]

Барицентр подмножества X пространства можно вычислить с помощью интеграла

где интегрирование ведётся по всему пространству , а g является характеристической функцией подмножества, принимающей 1 внутри X и 0 вне его^[6]. Заметим, что знаменатель равен мере множества X. Формула неприменима к множеству нулевой меры, а также к множествам, для которых интеграл расходится.

Другая формула для вычисления координат барицентра:

где G_k является k-й координатой G, а S_k(z) — мера пересечения X с гиперплоскостью, определяемой уравнением x_k = z. Снова знаменатель — это мера множества X.

Для плоской фигуры координатами барицентра будут

где A — площадь фигуры X, S_y(x) — длина пересечения^{[неизвестный термин]} X с вертикальной прямой с абциссой x, S_x(y) — аналогичная величина при обмене осей.

Определение местоположения барицентра для области, ограниченной графиками непрерывных функций[править | править код]

Координаты барицентра области, ограниченной графиками непрерывных функций и , таких что на интервале , , задаются выражениями

^[6].

^[7]

где  — площадь области (вычисляемая по формуле )^[8][9].

Определение местоположения барицентра объекта, имеющего форму буквы L[править | править код]

Метод нахождения барицентра фигуры, имеющей форму буквы L.

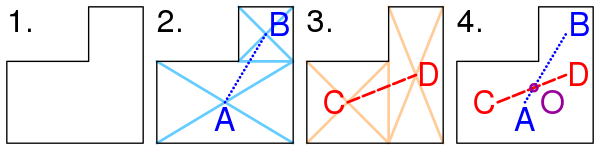
1. Фигуру делят на два прямоугольника (см. фигуру (2) на рисунке). Находят барицентры A и B этих двух прямоугольников как пересечение диагоналей. Рисуют отрезок AB, соединяющий барицентры. Барицентр фигуры должен лежать на этом отрезке AB.
2. Делят фигуру на два прямоугольника другим способом (см. фигуру (3) на рисунке). Находят барицентры C и D этих двух прямоугольников. Проводят отрезок CD, соединяющий барицентры. Барицентр фигуры должен лежать на отрезке CD.
3. Поскольку барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.

Барицентры треугольника и тетраэдра[править | править код]

Барицентр треугольника совпадает с пересечением медиан. Барицентр разбивает каждую медиану в отношении 2:1, то есть барицентр находится на расстоянии ⅓ от стороны до противоположной вершины (см. рисунок). Его декартовыми координатами является среднее координат трёх вершин. То есть, если вершинами треугольника являются , и , то координаты барицентра вычисляются по формуле

.

Таким образом, барицентр имеет барицентрические координаты .

В трилинейных координатах барицентр можно получить одним из эквивалентных способов^[10]:

Барицентр является также физически центром масс треугольника, сделанного из однородного листового материала, а также, если вся масса сконцентрирована в вершинах и одинаково разделена между ними. Если же масса распределена равномерно вдоль периметра, то центр масс лежит в точке Шпикера (инцентре серединного треугольника), который (в общем случае) не совпадает с центроидом всего треугольника.

Площадь треугольника равна 3/2 длины любой стороны, умноженной на расстояние от центроида до стороны^[11].

Центроид треугольника лежит на прямой Эйлера между его ортоцентром и центром его описанной окружности , ровно вдвое ближе ко второму, чем к первому:

.

Кроме того, для инцентра и центра девяти точек , мы имеем

,

,

,

,

.

Аналогичными свойствами обладает тетраэдр — его барицентр является пересечением отрезков, соединяющих вершины с барицентрами противоположных граней. Эти отрезки делятся барицентром в отношении 3:1. Результат может быть обобщён на любой -мерный симплекс. Если вершины симплекса обозначить и рассматривать вершины как вектора, центроид равен

.

Геометрический барицентр совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как равных масс.

Изогональным сопряжением центроида треугольника является точка пересечения его симедиан.

Барицентр тетраэдра[править | править код]

Тетраэдр является телом в трёхмерном пространстве, имеющим четыре треугольника в качестве граней. Отрезок, соединяющий вершину тетраэдра с барицентром противоположной грани, называется медианой, а отрезок, соединяющий середины двух противоположных сторон, называется бимедианой. Таким образом, имеется четыре медианы и две бимедианы. Эти шесть отрезков пересекаются в барицентре тетраэдра^[12]. Барицентр тетраэдра лежит посередине между точкой Монжа и центром описанной сферы. Эти точки задают прямую Эйлера тетраэдра, являющуюся аналогом прямой Эйлера треугольника.

Барицентр многоугольника[править | править код]

Барицентром самонепересекающегося замкнутого многоугольника, заданного вершинами , , , , является точка , где

;

и где является площадью многоугольника (со знаком):

^[13].

В этой формуле предполагается, что вершины пронумерованы вдоль периметра многоугольника. Кроме того, вершина считается той же самой, что и .
Заметим, что если точки пронумерованы по часовой стрелке, площадь , вычисленная выше, будет отрицательной, но координаты барицентра подкорректируют этот случай.

Барицентры конуса и пирамиды[править | править код]

Барицентр конуса или пирамиды расположен на отрезке, соединяющем вершину тела с барицентром основания. Для целого конуса или пирамиды барицентр находится на расстоянии 1/4 от основания к вершине. Для поверхности конуса или пирамиды (боковая поверхность без внутренности и без основания) центроид находится на 1/3 расстояния от основания до вершины.

См. также[править | править код]

• Центр масс
• Центроид треугольника
• Центр тяжести
• Центр Чебышева^[en]
• Среднее Фреше^[en]
• k-means
• Список барицентров
• Теоремы Паппа — Гульдина
• Замечательные точки треугольника

Примечания[править | править код]

Литература[править | править код]

• Зетель, С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд/. — М. : Учпедгиз, 1962. — С. 12.
• Leung Kam-tim, Suen Suk-nam. Vectors, matrices and geometry. — Hong Kong University Press, 1994.

• Nathan Altshiller-Court. College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. — 2nd. — New York: Barnes & Noble, 1925.
• Paul Bourke. Calculating the area and centroid of a polygon. — 1997.
• Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007.
• David C. Kay. College Geometry. — New York: Holt, Rinehart and Winston, 1969.
• Roland E. Larson, Robert P. Hostetler, Bruce H. Edwards. Calculus of a Single Variable. — 6th. — Houghton Mifflin Company, 1998.
• Murray H. Protter, Charles B. Morrey Jr. College Calculus with Analytic Geometry. — 2nd. — Reading: Addison-Wesley, 1970.

Ссылки[править | править код]

• Characteristic Property of Centroid at cut-the-knot
• Barycentric Coordinates at cut-the-knot
• Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge
• Experimentally finding the medians and centroid of a triangle at Dynamic Geometry Sketches, an interactive dynamic geometry sketch using the gravity simulator of Cinderella.

На карте отобразил условный контур и теперь хотел бы в него вывести балун. Создать балун не проблема, не поместить его в центр полигона — проблема.

В математике есть довольно сложные формулы для расчёта центра масс многоугольника, ими я не умею пользоваться. но в яндекс апи есть poly.geometry.getBounds(), который берёт максимально большой контур и находит центр. У меня тоже не получается его применить потому что полигон я создал не стандартным способом( new ymaps.Polygon()), а через map.geoObjects.add(objectManager);

Помогите пожалуйста получить координаты центра полигона.

Если нужно, то вот фиддл, который демонстрирует getBounds().

Медиана треугольника есть диаметр, делящий пополам хорды, параллельные основанию, поэтому на ней лежит центр тяжести (п° 217) площади треугольника. Следовательно, три медианы треугольника, пересекаясь, определяют центр тяжести площади треугольника.

Элементарные соображения показывают, что медианы треугольника пересекаются в точке, отстоящей на две трети длины каждой из них от соответствующей вершины. Поэтому центр тяжести площади треугольника лежит на любой его медиане на расстоянии двух третей ее длины от вершины.

219. Четырехугольник.

Центр тяжести площади четырехугольника определяется пересечением двух прямых, которые мы получаем, применяя распределительное свойство центров тяжести (п° 213).

Сначала делим четырехугольник диагональю на два треугольника. Центр тяжести четырехугольника лежит на прямой, соединяющей центры тяжести этих треугольников. Эта прямая и есть первая из двух искомых прямых.

Вторую прямую получим таким же способом, разбивая четырехугольник на два треугольника (отличных от предыдущих) посредством другой диагонали.

220. Многоугольник.

Мы знаем способы нахождения центров тяжести площади треугольника и четырехугольника. Чтобы определить центр тяжести площади многоугольника с произвольным числом сторон, предположим, что мы умеем находить центр тяжести площади многоугольника с меньшим числом сторон.

Тогда можно поступить так же, как в случае четырехугольника. Площадь данного многоугольника делят на две части двумя разными способами проведением диагоналей. В каждом из двух случаев соединяют прямой центры тяжести отдельных частей. Эти две прямые пересекаются в искомом центре тяжести.

221. Дуга окружности.

Пусть требуется определить центр тяжести дуги окружности АВ длины s. Отнесем окружность к двум взаимно перпендикулярным диаметрам ОХ и OY, из которых первый проходит через середину С дуги АВ. Центр тяжести лежит на оси ОХ, являющейся осью симметрии. Достаточно поэтому определить 5. Для этого имеем формулу:

Пусть будут: а — радиус окружности, с — длина хорды АВ, — угол между осью ОХ и радиусом, проведенным к элементу значения , соответствующие концам дуги АВ. Имеем:

Тогда, принимая В за переменную интегрирования и выполняя интегрирование вдоль дуги АВ, получим:

Следовательно, центр тяжести дуги окружности лежит на радиусе, проведенном через середину дуги, в точке, расстояние которой от центра окружности есть четвертая пропорциональная длины дуги, радиуса и хорды.

222. Круговой сектор.

Сектор, заключенный между дугой окружности и двумя радиусами ОА и ОВ, может быть разложен промежуточными радиусами на бесконечно малые равные между собою секторы. Эти элементарные секторы можно рассматривать как бесконечно узкие треугольники; центр тяжести каждого из них, по предыдущему, лежит на радиусе, проведенном через середину элементарной дуги этого сектора, на расстоянии двух третей длины радиуса от центра окружности. Равные между собою массы всех элементарных треугольников, сосредоточенные в их центрах тяжести, образуют однородную дугу окружности, радиус которой равен двум третям радиуса дуги сектора. Рассматриваемый случая приводится, таким образом, к отысканию центра тяжести этой однородной дуги, т. е. к задаче, решенной в предыдущем п°.

223. Тетраэдр.

Определим центр тяжести объема тетраэдра. Плоскость, проходящая через одно из ребер и через середину противоположного ребра, есть диаметральная плоскость, которая делит пополам хорды, параллельные этому последнему ребру: она содержит поэтому центр тяжести объема тетраэдра. Следовательно, шесть плоскостей, тетраэдра, из которых каждая проходит через одно из ребер и через середину противоположного ребра, пересекаются в одной точке, представляющей собой центр тяжести объема тетраэдра.

Рассмотрим тетраэдр ABCD (фиг. 37); соединим вершину А с центром тяжести I основания BCD; прямая AI есть пересечение диаметральных плоскостей, проходящих

через ребра АВ и поэтому она содержит искомый центр тяжести. Точка находится на расстоянии двух третей медианы ВН от вершины В. Точно так же возьмем на медиане АН точку К на расстоянии двух третей ее длины от вершины . Прямая В К пересечет прямую А в центре тяжести тетраэдра. Проведем из подобия треугольников АВН и ЮН видно, что IK есть третья часть АВ) далее, из подобия треугольников и ВГА заключаем, что есть третья часть .

Следовательно, центр тяжести объема тетраэдра лежит на отрезке, соединяющем любую вершину тетраэдра с центром тяжести противоположной грани, на расстоянии трех четвертей длины этого отрезка от вершины.

Заметим еще, что прямая, соединяющая середины Я и L двух противоположных ребер (фиг. 38) есть пересечение диаметральных плоскостей, проходящих через эти ребра, она также проходит через центр тяжести тетраэдра. Таким образом, три прямые, соединяющие середины противоположных ребер тетраэдра, пересекаются в его центре тяжести.

Пусть Н и — середины одной пары противоположных ребер (фиг. 38) и М, N — середины двух других противоположных ребер. Фигура HNLM есть параллелограм, стороны которого соответственно параллельны остальным

двум ребрам. Прямые HL и MN, соединяющие середины двух противоположных ребер, суть диагонали этого параллелограма, а значит, они в точке пересечения делятся пополам. Таким образом, центр тяжести тетраэдра лежит в середине отрезка, соединяющего середины двух противоположных ребер тетраэдра.

224. Пирамида с многоугольным основанием.

Центр тяжести пирамиды лежит на отрезке, соединяющем вершину пирамиды с центром тяжести основания на расстоянии трех четвертей длины этого отрезка от вершины.

Чтобы доказать эту теорему, разложим пирамиду на тетраэдры плоскостями, проведенными через вершину пирамиды и через диагонали основания ABCD (например BD на фиг. 39).

Проведем плоскость пересекающую ребра на расстоянии трех четвертей их длины от вершины. Эта плоскость содержит центры тяжести тетраэдров, а следовательно, и пирамиды. Массы тетраэдров, которые мы предполагаем сосредоточенными в их центрах тяжести, пропорциональны их объемам, следовательно и площадям из оснований (фиг. 39) или также площадям треугольников bad, bed. подобных предыдущим и расположенным в секущей плоскости abcd. Таким образом, искомый центр тяжести совпадает с центром тяжести многоугольника abcd. Последний же лежит на прямой, соединяющей вершину S пирамиды с центром тяжести (подобно расположенным) многоугольника основания.

225. Призма. Цилиндр. Конус.

На основании симметрии, центры тяжести призмы и цилиндра лежат на середине отрезка, соединяющего центры тяжести оснований.

Рассматривая конус, как предел вписанной в него пирамиды с той же вершиной, убеждаемся, что центр тяжести конуса лежит на отрезке, соединяющем вершину конуса с центром тяжести основания, на расстоянии трех четвертей длины этого отрезка от вершины. Можно также сказать, что центр тяжести конуса совпадает с центром тяжести сечения конуса плоскостью, параллельной основанию и проведенной на расстоянии одной четверти высоты конуса от основания.

Понятие “центр тяжести многоугольника” можно интерпретировать тремя различными способами:

1. Масса находится только в вершинах, причем каждая вершина “весит” одинаково
2. Масса равномерно распределена по границе многоугольника
3. Масса равномерно распределена по области, ограниченной многоугольником.

Рассмотрим все три интерпретации в порядке возрастания сложности алгоритма.

1. Масса находится только в вершинах, причем каждая вершина весит одинаково

В этом случае координаты центра тяжести выражаются по формулам:

Таким образом для нашего частного случая имеем:

2. Масса равномерно распределена по границе многоугольника

В этом случае масса ребра пропорциональна его длине. Таким образом каждое ребро мы можем заменить на точечную массу (пропорциональную длине ребра). Затем применяя те же формулы для определения центра тяжести получаем:

Ниже представлена программа, реализующая описанный алгоритм:

3. Масса равномерно распределена по области, ограниченной многоугольником.

Этот случай уже не является столь тривиальным, как два предыдущих. Для построения алгоритма понадобится следующий факт:

Предложение 1
Пусть фигура Ф есть объединение двух других фигур Ф1 и Ф2 (пересекающихся только по границе).
Тогда центр тяжести фигуры Ф выражается так:

(Это утверждение очевидно следует из определения центра тяжести произвольной фигуры и свойства аддитивности интеграла)

Кроме того для треугольника центр тяжести определяется так:

Разобьем наш многоугольник на треугольники. Для каждого треугольника найдем его центр тяжести (Xci, Yci) и площадь (Si). После этого, согласно Предложению 1, координаты центра тяжести многоугольника можно найти следующим образом:

Остается вопрос, как разбить многоугольник на треугольники. Если многоугольник выпуклый, а вершины перечислены в порядке обхода по или против часовой стрелки, то достаточно просто найти одну точку внутри многоугольника (Xm,Ym), а затем разбить многоугольник на N следующих треугольников:

Если же многоугольник выпуклый, но вершины перечислены не в порядке обхода, то их придется упорядочить. Сделать это можно, например, отсортировав вершины по углу между положительной полуосью ОХ и вектором (Xi-Xm, Yi-Ym).

Невыпуклый многоугольник всегда можно разбить на несколько выпуклых. А затем, применив описанный алгоритм для каждой выпуклой части, и используя Предложение 1, найти центр тяжести всего многоугольника. Задача о разбиении произвольного многоугольника на выпуклые части является самостоятельной задачей, которая рассмотрена в соответствующем разделе. Поэтому представленная ниже реализация алгоритма работает только для выпуклых многоугольников.

Ниже представлен пример реализации описанного алгоритма на языке С для нахождения центра тяжести выпуклого многоугольника, вершины которого перечислены в порядке обхода по или против часовой стрелки:

Ваше определение центра вообще не имеет смысла.

Чтобы увидеть это, просто нарисуйте три невыровненные точки на плоскости и вычислите одну – единственную окружность, которая проходит для всех трех точек. Ясно, что ваш центр треугольника должен быть центром этого круга.

Теперь нарисуйте четвертую точку, которая не лежит на окружности и образует четырехгранный многоугольник. Что такое центр? На плоскости нет точки, равноудаленной от всех вершин.

Также обратите внимание, что даже в случае треугольников с использованием точки, равноудаленной от вершин, вы можете получить точки вне и далеко от многоугольника, а также численно нестабильно (при любых ε> 0 и M> 0 вы всегда можете построить треугольник, в котором специфическое перемещение вершины на расстояние меньше ε перемещает центр на расстояние больше M).

Обычно используемые “центры”, которые легко вычислить, – это среднее значение всех вершин, среднее значение границы, центр масс или даже просто центр ограничивающего прямоугольника, выровненного по оси. Однако все они могут выходить за пределы многоугольника, если многоугольник не выпуклый, но в вашем случае они могут работать.

Самый простой разумный (поскольку он не зависит от системы координат) – это барицентр вершин (код на Python):

xc = sum(x for (x, y) in points) / len(points)
yc = sum(y for (x, y) in points) / len(points)

что-то плохое в том, что просто разделение одной стороны многоугольника дает вам другой центр (другими словами, это зависит от вершин, а не от набора точек, ограниченных многоугольником). Самым простым, что зависит от многоугольника, является центр масс границы IMO:

sx = sy = sL = 0
for i in range(len(points)):   # counts from 0 to len(points)-1
    x0, y0 = points[i - 1]     # in Python points[-1] is last element of points
    x1, y1 = points[i]
    L = ((x1 - x0)**2 + (y1 - y0)**2) ** 0.5
    sx += (x0 + x1)/2 * L
    sy += (y0 + y1)/2 * L
    sL += L
xc = sx / sL
yc = sy / sL

Для них обоих расширение до 3d тривиально … просто добавьте z, используя те же формулы.

В случае общего (не обязательно выпуклого, не обязательно односвязного) многоугольника «центром», который я нашел полезным, но который нетривиально вычислить, является () внутренняя точка, которая находится на максимальном расстоянии от границы (в другими словами «самая внутренняя» точка).

В этом случае я прибег к использованию дискретного (растрового) представления и преобразования гауссова расстояния.

person
6502
  
schedule
19.08.2013

II. SOLVE THE PROBLEM

Why doesn’t a simple mean give the position of a centroid in a polygon? leads to formulas.

Frown. I want to know how to set up and solve the problem. A solution can always be converted to a formula. The reverse –figuring out how a problem was solved by looking at the formula– is very hard. So I will solve problem from scratch.

A working demonstration of the method below can be found here. The linked document is a Geogebra worksheet; feel free to download it, examine the code, and use it as you see fit.

A. Observation
The centroid of triangle $Delta ABC$ is the simple average of its vertices:
$;;;D = (A+ B + C)/3$.
What? Point order does not matter here: take the vertices A,B,C, in any order, they are the same triangle. To prove the formula is correct, I might Integrate the triangle area; Find the balance point of figure ABC; or, with compass and straightedge, draw the intersection of the medians. I say, the point is the same in every case.

B. Procedure
I will convert the problem into one I know how to solve:
Proposition: Find the centroid of a set of weighted points.

1. Chop Jerome up into mutually exclusive triangles.

2. Say there are m triangles. For each triangle $;Delta_k, ;k =1, 2, ldots, m,;$ find the centroid $C_k$, and the area (weight) $w_k$. The set of weighted points is then $[frac{w_k C_k}{J}],$ where J is the area of Jerome.

3. Solution: Add ’em up.
   I say, the resulting point is the centroid of the polygon.

I have a general solution (I can always carry out this procedure). But it’s messy: I don’t have a triangulation rule. Now what? A good way to generalize is to start with a case I can solve.

C. Case: Jerome is Convex
It is commonly known that, given a convex polygon $P$, we may choose any vertex, $V,$ draw segments from $V$ to every non-adjacent vertex, and $P$ is correctly triangulated.

I will also use the following formulas:
-Let any two sides of $Delta ABC$ be vectors ${rm u =(u_1, u_2),;; v= (v_1, v_2)}.;$ Then
$;;;{rm Area}_{Delta ABC} = tfrac{1}{2}|{rm u times v}|,;;;;;$where (the determinant) ${rm u times v}={rm u_1 v_2-u_2 v_1}$.

-Let sides $AB, AC$ of $Delta ABC$ be vectors ${rm u, v}.;$ Then the centroid D= (A+B+C)/3 can be written
$;;;D = A + tfrac{1}{3}|{rm u + v}|.$

I have gathered what I need.

D. Solution

1. Let the counterclockwise path of my n-gon be given, in order, by
   $;;[A_i] = A_1, A_2, ldots, A_n$
   For covenience, I choose $V=A_1$.

2. Draw the n-1 vectors from A_1 to the other vertices:
   $;;[{rm a_i}] = (A_{k+1}-A_1),;; k = 1, 2, ldots n!-!1$

3. I have n-2 adjacent triangles with centroids
   $;;[C_i] = A_1 + tfrac{1}{3}{rm (a_k+a_{k+1})},;; k = 1, 2, ldots n!-!2$
   And areas (weights)
   $;;[w_i] = tfrac{1}{2}{rm (a_ktimes a_{k+1})},;; k = 1, 2, ldots n!-!2$
   (I dropped the absolute value: counter-clockwise, ${rm u times v}$ is positive.) Then
   Total area = $sum_{k=1}^{n-2} w_k$ and

4. The centroid $C_J$ of Jerome is the sum of weighted triangle ‘roids, divided by total area:
   $;;C_J= {large frac{sum_{k=1}^{n-2} w_k C_k}{sum_{k=1}^{n-2} w_k}}$,

which can be written

$$(2);;C_J= A_1+{large frac{1}{3} frac{sum_{k=1}^{n-2} ({rm a_k+ a_{k+1}})({rm a_k times a_{k+1}})}{sum_{k=1}^{n-2} ({rm a_k times a_{k+1}})}
}$$

I say, that this is in fact the complete solution: the determinants give signed areas: +/- according as the direction of rotation from $A_k$ to $A_{k+1}$, about $A_1$ is positive or negative, preserving measure in either case.

Being the thing to be done.

1. 1 накопление и центр тяжести
Предположим, что есть N дискретных точек данных (xi, yi) (i = 1, 2,., N) на плоскости, и
Центр тяжести многоугольника G (. X1 ,. Y1):

Это самый простой и интуитивно понятный способ поиска полигонов. Дискретные числа можно использовать напрямую
Координаты x и y базовой точки позволяют найти центр тяжести графика. Но недостаток заключается в отсутствии
Графика вокруг точек данных недостаточно точна для обработки и анализа.

1. 2 Алгоритм 1: Говоря об этом алгоритме, мы должны сначала понять следующие теоремы.
Теорема 1 «Координаты вершин Ai (xi, yi) (i = 1, 2, 3) треугольника △ A1A2A3 известны. Его координаты центра тяжести:

　　xg = (x1+x2+x3) / 3 ;                       yg = (y1+y2+y3) / 3 ;

Теорема 2 «Координаты вершин Ai (xi, yi) (i = 1, 2, 3) треугольника A1A2A3 известны. Площадь треугольника:

　　S =  ( (x2 – x1) * (y3 – y1) – (x3 – x1) * (y2 – y1) ) / 2 ;

△ A1A2A3 Когда граница образует петлю против часовой стрелки, возьмите +, а по часовой стрелке –。

Кроме того, в процессе решения нет необходимости учитывать, какой порядок ввода точек – по часовой стрелке или против часовой стрелки, и деление аннулируется.

Принцип: разделите многоугольник на n небольших областей, каждая из которых имеет площадь σi и центр тяжести Gi (.xi, .yi), и используйте формулу, чтобы найти центр тяжести тонкой пластины.
На совокупную сумму:

Основываясь на принципах и математических теоремах, предложенных выше, можно получить общую формулу центра тяжести для многоугольника, окруженного дискретными точками данных: любой N-сторонний многоугольник A1A2 с Ai (xi, yi) (i = 1, 2,., n) как вершину .An, разделите ее на N-2 треугольника (рисунок 1). Центр тяжести каждого треугольника – Gi (. Xi ,. Yi), а площадь – σi. Тогда координаты центра тяжести G (.x2, .y2) многоугольника равны:

               Рис.1 Разложение по многоугольнику

Примеры вопросов:HDU 1115 Lifting the Stone

код показан ниже.

 1 #include<stdio.h>
 2 #include<math.h>
 3 #include<stdlib.h>
 4 struct centre
 5 {
 6        double x , y ;
 7 };
 8 int cas , n ;
 9 double Area( centre p0 , centre p1 , centre p2 )
10 {
11        double area = 0 ;
12        area =  p0.x * p1.y + p1.x * p2.y + p2.x * p0.y - p1.x * p0.y - p2.x * p1.y - p0.x * p2.y;
13        return area / 2 ;  // Кроме того, в процессе решения нет необходимости учитывать, какой порядок ввода точек - по часовой стрелке или против часовой стрелки, и деление аннулируется.
14 }
15 int main ()
16 {
17     centre p0 , p1 , p2 ;
18     double sum_x , sum_y , sum_area , area;
19     scanf ( "%d" , &cas ) ;
20     while ( cas -- )
21     {
22           sum_x = sum_y = sum_area = 0 ;
23           scanf ( "%d" , &n ) ;
24           scanf ( "%lf%lf" , &p0.x , &p0.y ) ;
25           scanf ( "%lf%lf" , &p1.x , &p1.y ) ;
26           for ( int i = 2 ; i < n ; ++ i )
27           {
28               scanf ( "%lf%lf" , &p2.x , &p2.y ) ;
29               area = Area(p0,p1,p2) ;
30               sum_area += area ;
31               sum_x += (p0.x + p1.x + p2.x) * area ;
32               sum_y += (p0.y + p1.y + p2.y) * area ;
33               p1 = p2 ;
34           }
35           printf ( "%.2lf %.2lfn" , sum_x / sum_area / 3 , sum_y / sum_area / 3 ) ;
36     }
37     return 0 ;
38 }