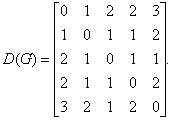Определение
Эксцентриситетом вершины называется расстояние до самой дальней вершины графа.
Радиусом графа называется минимальный эксцентриситет среди всех вершин графа
Диаметром графа – это наибольшее расстояние между всеми парами вершин графа
Центральной вершиной графа является вершина чей эксцентриситет равен радиусу графа.
Периферийной вершиной графа является вершина чей эксцентриситет равен диаметру графа.
Поиск радиуса и диаметра
Сервис граф онлайн позволит вам найти радиус и диаметр, а также укажет центральные и периферийные вершины. Для этого выберете пункт меню Алгоритмы -> Поиск радиуса и диаметра графа.
Реализацию алгоритма на JavaScript можно найти по ссылке: http://graphonline.ru/script/plugins/RadiusAndDiameter.js
-
Диаметр, радиус и центр графа
Для связного графа
определим
расстояние
между двумя его вершинами
и
как длину самой короткой цепи, соединяющей
эти вершины, и обозначим через
.
Длина цепи – это количество ребер,
составляющих цепь. Нетрудно проверить,
что введенное расстояние удовлетворяет
аксиомам метрики:
1)
2)
;
3)
.
Определим расстояние
от каждой вершины
графа
до самой далекой от нее вершины
,
которое называется
эксцентриситетом.
Очевидно, что эксцентриситет для всех
вершин в полного графа равен единице,
а для вершин простого цикла
–
.
Максимальный
эксцентриситет
носит название диаметра
графа, а
минимальный
– радиуса
графа
.
В полном графе имеем
,
а в простом цикле
–
.
Вершина
называется центральной, если
.
Граф может иметь несколько таких вершин,
а в некоторых графах все вершины являются
центральными. В простой цепи при нечетном
числе вершин только одна является
центральной, а при четном их числе таких
вершин две. В полном графе и для простого
цикла центральными являются все вершины.
Множество центральных вершин называется
центром
графа.
Пример 1.
Найти диаметр,
радиус и центр графа, приведенного на
рис. 4.
°
°
°
°
°
°
°
°
°
Рис.
4.
Для решения этой
задачи удобно предварительно вычислить
матрицу
расстояний
между вершинами графа. В данном случае
это будет матрица размером
,
в которой на месте
стоит расстояние от вершины
до вершины
:
Для каждой строки
матрицы находим наибольший элемент и
записываем его справа от черточки.
Наибольшее из этих чисел равно диаметру
графа
,
наименьшее – радиусу графа
.
Центр графа составляют центральные
вершины
и
.
Понятия центральной
вершины и центра графа появились в связи
с задачами оптимального размещения
пунктов массового обслуживания, таких
как больницы, пожарные части, пункты
охраны общественного порядка и т. п.,
когда важно минимизировать наибольшее
расстояние от любой точки некоторой
сети до ближайшего пункта обслуживания.
-
Матрицы достижимостей и контрадостижимостей
Матрица достижимостей
определяется следующим образом:
Множество вершин
графа
,
достижимых из заданной вершины
,
состоит из таких элементов
,
для которых
-й
элемент в матрице
равен 1. Это множество можно представить
в виде
.
Матрица
контрадостижимостей
(обратных
достижимостей)
определяется следующим образом:
Аналогично построению
достижимого множества
можно сформировать множество
,
используя следующее выражение:
.
Из определений
следует, что
-й
столбец матрицы
совпадает с
-й
строкой матрицы
,
т. е.
,
где
– матрица, транспонированная к матрице
.
Пример 2.
Найти матрицы достижимостей и
контрадостижимостей для графа,
приведенного на рис. 5.
°
°
°
°
°
°
°
Рис.
5.
Определим множества
достижимостей для вершин графа:
,
,
,
,
,
,
.
Следовательно,
матрицы достижимостей и контрадостижимостей
имеют вид:


Так как
– множество таких вершин, каждая из
которых принадлежит по крайней мере
одному пути, идущему от
к
,
то вершины этого множества называются
существенными
или неотъемлемыми
относительно концевых вершин
и
.
Все остальные вершины
называются несущественными
или избыточными,
поскольку их удаление не влияет на пути
от
к
.
Можно определить
также матрицы ограниченных
достижимостей и контрдостижимостей,
если потребовать, чтобы длины путей не
превышали некоторого заданного числа.
Тогда
будет верхней границей длины допустимых
путей.
Граф называют
транзитивным,
если из существования дуг
и
следует существование дуги
.
Транзитивным
замыканием
графа
является граф
,
где
– минимально возможное множество дуг,
необходимых для того, чтобы граф
был транзитивным. Очевидно, что матрица
достижимостей
графа
совпадает с матрицей смежности
графа
,
если в матрице
на главной диагонали поставить единицы.
6
Соседние файлы в папке LK
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- 1 Диаметр дерева
- 1.1 Алгоритм
- 1.2 Реализация
- 1.3 Обоснование корректности
- 1.4 Оценка времени работы
- 2 Центр дерева
- 2.1 Определения
- 2.2 Алгоритм
- 2.2.1 Наивный алгоритм
- 2.2.2 Алгоритм для дерева за O(n)
- 3 См. также
- 4 Источники информации
Диаметр дерева
| Определение: |
| Диаметр дерева (англ. diameter of a tree) — максимальная длина (в рёбрах) кратчайшего пути в дереве между любыми двумя вершинами. |
Пусть дан граф . Тогда диаметром называется , где — кратчайшее расстояние между вершинами.
Алгоритм
- Возьмём любую вершину и найдём расстояния до всех других вершин.
- Возьмём вершину такую, что для любого . Снова найдём расстояние от до всех остальных вершин. Самое большое расстояние — диаметр дерева.
Расстояние до остальных вершин будем искать алгоритмом .
Реализация
//граф g представлен списком смежности
int diameterTree(list<list<int>> g):
v = u = w = 0
d = bfs(g, v)
for i = 0, i < n, i++
if d[i] > d[u]
u = i
d = bfs(g, u)
for i = 0, i < n, i++
if d[i] > d[w]
w = i
return d[w]
Обоснование корректности
Будем пользоваться свойством, что в любом дереве больше одного листа. Исключительный случай — дерево из одной вершины, но алгоритм сработает верно и в этом случае.
| Теорема: |
|
Искомое расстояние — расстояние между двумя листами. |
| Доказательство: |
| Пусть искомое расстояние — расстояние между вершинами , где не является листом. Так как не является листом, то её степень больше единицы, следовательно, из неё существует ребро в непосещённую вершину (дважды посетить вершину мы не можем). |
После запуска алгоритма получим дерево .
| Теорема: |
|
В дереве не существует ребер между вершинами из разных поддеревьев некоторого их общего предка. |
| Доказательство: |
|
Предположим, существует ребро между соседними поддеревьями: Рассмотрим первую вершину, в которую приведет наш алгоритм, пусть это вершина , тогда в ходе рассмотрения всех смежных вершин мы добавим в список вершину , тем самым исключив возможность попадания их в разные поддеревья. |
Мы свели задачу к нахождению вершины , такой что сумма глубин поддеревьев максимальна.
Докажем, что одно из искомых поддеревьев содержит самый глубокий лист.
Пусть нет, тогда, взяв расстояние от до глубочайшего листа, мы можем улучшить ответ.
Таким образом мы доказали, что нам нужно взять вершину с наибольшей глубиной после первого , очевидно, что ей в пару надо сопоставить вершину , такую что максимально. Вершину можно найти запуском из .
Оценка времени работы
Все операции кроме — .
работает за линейное время, запускаем мы его два раза. Получаем .
Центр дерева
Определения
| Определение: |
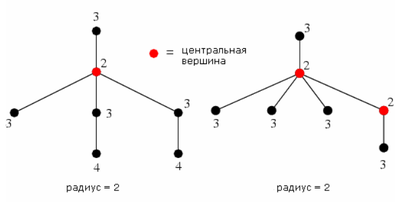
| Эксцентриситет вершины (англ. eccentricity of a vertex) — , где — множество вершин связного графа . |
| Определение: |
| Радиус (англ. radius) — наименьший из эксцентриситетов вершин графа . |
| Определение: |
| Центральная вершина (англ. central vertex) — вершина графа , такая что |
| Определение: |
| Центр графа (англ. center of a graph) — множество всех центральных вершин графа . |
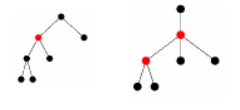
Примеры деревьев с одной и двумя центральными вершинами
Графы, у которых показан эксцентриситет каждой вершины
Алгоритм
Наивный алгоритм
Найдём центр графа исходя из его определения.
- Построим матрицу ( — мощность множества ), где , то есть матрицу кратчайших путей. Для её построения можно воспользоваться алгоритмом Флойда-Уоршелла или Дейкстры.
- Подсчитаем максимум в каждой строчке матрицы . Таким образом, получим массив длины .
- Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами.
Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет , а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и , за которую мы находим максимумы в матрице.
Алгоритм для дерева за O(n)
| Теорема: |
|
Каждое дерево имеет центр, состоящий из одной вершины или из двух смежных вершин. |
| Доказательство: |
| Утверждение очевидно для деревьев с одной и двумя вершинами. Покажем, что у любого другого дерева те же центральные вершины, что и у дерева , полученного из удалением всех его висячих вершин. Расстояние от данной вершины дерева до любой другой вершины достигает наибольшего значения, когда – висячая вершина. Таким образом, эксцентриситет каждой вершины дерева точно на единицу меньше эксцентриситета этой же вершины в дереве , следовательно, центры этих деревьев совпадают. Продолжим процесс удаления и получим требуемое. |
Собственно, алгоритм нахождения центра описан в доказательстве теоремы.
- Пройдёмся по дереву обходом в глубину и пометим все висячие вершины числом .
- Обрежем помеченные вершины.
- Образовавшиеся листья пометим числом и тоже обрежем.
- Будем повторять, пока на текущей глубине не окажется не более двух листьев, и при этом в дереве будет тоже не более двух листьев.
Оставшиеся листья являются центром дерева.
Для того, чтобы алгоритм работал за , нужно обрабатывать листья по одному, поддерживая в очереди два последовательных по глубине слоя.
См. также
- Дерево, эквивалентные определения
- Дополнительный, самодополнительный граф
Источники информации
- Wikipedia — Distance (graph theory)
- Ф. Харари: Теория графов
- А. Клебанов: Центры графов(нерабочая ссылка)
Граф с центральными точками, представленными красным цветом. Это такие точки A, что d(A, B) ≤ 3 для любых вершин B. Любая чёрная вершина находится на расстоянии по меньшей мере 4 от одной из других вершин.
Центр (или центр Жордана[1]) графа — это множество всех вершин с минимальным эксцентриситетом[2]. То есть множество всех вершин A, для которой максимальное расстояние d(A,B) до других вершин B минимально. Эквивалентно, это множество вершин с эксцентриситетом, равным радиусу графа[3].
Нахождение центра графа полезно для задач размещения предприятий, целью которых является минимизация наиболее дальних расстояний до предприятия. Например, размещение госпиталя в центре объекта уменьшает максимальное расстояние, которое приходится преодолевать машинам медицинской помощи.
Концепция центра графа связана с измерением центральности по близости в анализе социальных сетей, которая равна обратной величине к среднему расстояний d(A,B)[1].
Примечания[править | править код]
- ↑ 1 2 Wasserman & Faust, 1994, p. 185.
- ↑ McHugh, James A., Algorithmic Graph Theory Архивировано 1 августа 2010 года.
- ↑ Weisstein, Eric W. Graph center (англ.) на сайте Wolfram MathWorld.
Литература[править | править код]
- Stanley Wasserman[en], Katherine Faust. . Social Network Analysis: Methods and Applications. — Cambridge: Cambridge University Press, 1994. — ISBN 0-521-38269-6. — P. 185.
Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).
Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:
1) d(v, w) 0, причем d(v, w) = 0 тогда и только тогда, когда v=w;
2) d(v, w) = d(w, v);
3) d(v, w) d(v, u) + d(u, w).
Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.
Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.
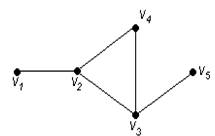
Пример 82.
Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.
Рис. 3.16. Граф для примера 82
Решение.
Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами dij которой будут расстояния между вершинами vi и vj. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали.
С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения: для i, j = 1, 2, …, 5. В результате получаем: r(v1) = 3, r(v2) = 2, r(v3) = 2, r(v4) = 2, r(v5) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v2, v3, v4.