Центральный угол конуса в развертке как найти

Центральный угол конуса в развертке как найти

Построение развертки конуса

Развертка поверхности конуса – это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.

Варианты построения развертки:

  • Прямой круговой конус
  • Наклонный конус
  • Усеченный конус

Развертка прямого кругового конуса

Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.

В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.

Алгоритм построения

  1. Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
  2. Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.

Пример

На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.

Рассмотрим треугольник S0A0B0. Длины его сторон S0A0 и S0B0 равны образующей l конической поверхности. Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.

Грани S0B0C0, S0C0D0, S0D0E0, S0E0F0, S0F0A0 пирамиды SABCDEF строим аналогично треугольнику S0A0B0.

Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

Алгоритм

  1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
  2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
    Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
  3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S01060, S06050, S05040, S04030, S03020, S02010. Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

Алгоритм

  1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
  2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
  3. Находим положение точек A0, B0, C0 на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S0A0=S’’A’’, S0B0=S’’B’’1, S0C0=S’’C’’1.
  4. Соединяем точки A0, B0, C0 плавной линией.

Развертка усеченного конуса

Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.

Алгоритм

  1. Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
  2. Строим развертку боковой поверхности конуса ε – S0A01020304050A0 и на биссектрисе угла A0S0A0 отмечаем точку O0, выбрав ее расположение произвольно.
  3. Проводим прямые O0A0, O010, O020, O030, O040, O050, O0A0 и на них откладываем отрезки [O0A10]=t×|O0A0|, [O0110]= t×|O010|, [O0210]=t×|O020|, [O0310]=t×|O030|, [O0410]=t×|O040|, [O0510]=t×|O050|, [O0A10]=t×|O0A0| соответственно, где t=D/d. Соединяем точки A10, 110, 210, 310, 410, 510, A10 плавной линией.
  4. Из точек A10, 110, 210, 310, 410, 510, A10 проводим лучи, которые параллельны соответственно прямым A0S0, 10S0, 20S0, 30S0, 40S0, 50S0, A0S0, и на них откладываем отрезки A10B10, 110120, 210220, 310320, 410420, 510520, A10B10, равные l – образующей усеченного конуса. Проводим линию B10120220320420520B10.
Источник
Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

  • Все категории
  • экономические
    43,651
  • гуманитарные
    33,653
  • юридические
    17,917
  • школьный раздел
    611,896
  • разное
    16,900

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Источник

По какой формуле находится центральный угол развертки боковой поверхности конуса?!Если помож. отв. признаю лучшим…

Megana 21



Ученик

(20),
закрыт



9 лет назад

Снежная Зима

Ученик

(149)


10 лет назад

alpha=360o*sin(gamma/2), где gamma- угол на верхушке конуса, получаемый на его осевом сечении. Например, если это сечение представляет собой равносторонний треуголыник (диаметр основания равен образующей) , то развертка – полукруг.

Источник

Развертка конуса.

Если задана поверхность прямого конуса,
то развертка его боковой поверхности
представляет круговой сектор, радиус
которого равен длине образующей
конической поверхности l, а
центральный угол φ=360о
r / l, где r –
радиус окружности основания конуса.
Для простоты построения используется
аппроксимация длинны окружности
основания конуса, для чего конус
вписывается в 12-угольную пирамиду
(рис.6).

Рисунок 5. Построение развертки конуса.

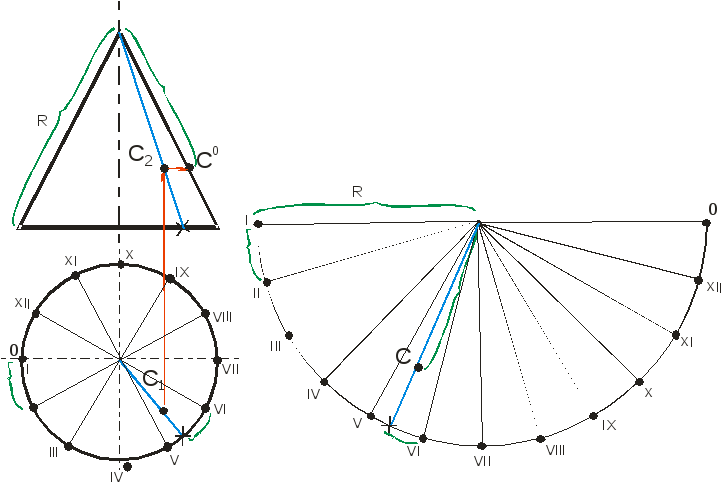
Построение развертки конуса начинаем
с деления основания на 12 частей радиусом.
Точки деления обозначаем римскими
цифрами. Радиусом, равном очерковой
образующей, строим сектор круга. Длина
дуги определяется, последовательно
откладывая на ней полученные при делении
отрезки. Для построение точки С,
принадлежащей поверхности конуса,
строим на развертке образующую, на
которой располагается точка. Чтобы
определить натуральную величину
расстояния от точки С до вершины конуса,
переносим ее на очерковую образующую
(метод вращения разбирали при построении
развертки пирамиды).

Построение
линии взаимного пересечения
кривых
поверхностей

Линией взаимного пересечения кривых
поверхностей является множество точек,
общих для данных поверхностей. Из этого
множества выделяют характерные (опорные,
или главные) точки, с которых следует
начинать построение этой линии. К таким
точкам относятся:

экстремальные
точки – верхняя и нижняя точки
линии пересечения относительно той или
иной плоскости проекций;

точки, расположенные на очерковых
образующих поверхностей, которые
определяют границы видимости, точки
пересечения оснований, и т.д.

Для уточнения формы линии пересечения
используются вспомогательные точки.

Для определения точек часто пользуются
вспомогательными секущими поверхностями.
Поверхности-посредники пересекают
данные поверхности по линиям, которые,
в свою очередь, пересекаются в точках
линии пересечения данных поверхностей.

Секущие поверхности-посредники выбираются
так, чтобы они, пересекаясь с данными
поверхностями, давали простые для
построения линии, например прямые и
окружности.

Из общей схемы построения линии
пересечения поверхностей выделяют два
основных метода – метод секущих
плоскостей и метод секущих
сфер.

Следует имеет в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в зоне общей для этих пересекающихся поверхностей

Характер линии пересечения кривых
поверхностей зависит от формы поверхностей
и от из взаимного положения. Линия
пересечения имеет форму замкнутой или
незамкнутой кривой, за исключением
случаев, когда пересекаются два цилиндра,
оси вращения которых параллельны, когда
пересекаются два конуса вершины которых
совпадают. В этих случаях линия пересечения
прямая.

Задача на построение линии пересечения
значительно упрощается, если одна
поверхность занимает проецирующее
положение. Для этого целесообразно
воспользоваться преобразованием
чертежа, чтобы представить пересекающиеся
поверхности в частном положении или
воспользоваться третьей проекцией.

Например (рис.1), на П3 цилиндр
занимает проецирующее положение.

Рисунок 1. Построение линии пересечения
цилиндра и конуса с

использованием третьей проекции.

Рассмотрим некоторые случаи взаимного
расположения поверхностей, которые
определяют характер линии пересечения.

1. Поверхности могут полностью
или не полностью пересекаться (рис.
2). В случае неполного проникновения
(рис.2. а.) линия пересечения – замкнутая
или незамкнутая пространственная кривая
линия, симметричная очерковой образующей.
В случае полного проникновения (рис.2
б.) линия пересечения состоит из двух
симметричных частей. На рисунке 2. в) две
симметричные части кривой соединяются
в точке касания. Проникновение с точкой
касания.

а) б)
в)

Рисунок 2. Пересечение конуса и цилиндра

а) Неполное проникновение; б) Полное
проникновение; в) Проникновение

с точкой касания.

2. Оси поверхностей вращения
параллельны:

– находятся в одной меридиональной
плоскости (рис.3 а.). Линия пересечения
симметрична относительно главного
меридиана и совпадает.

– находятся в разных плоскостях (рис.3
б.). Линия пересечения симметрична
относительно линии, соединяющей центры
поверхностей.

а.)
б.)

Рисунок 3. а) Ось конуса и цилиндра
находятся в одной меридиональной
плоскости, б) Ось конуса и цилиндра
находятся в разных плоскостях.

3. Оси поверхностей вращения
совпадают. Такие поверхности
называются соосными. Линия пересечения
таких поверхностей окружность (рис. 4).

Рисунок 4. Пересечение соосных поверхностей
цилиндра, конуса и сферы.

4. Особый случай пересечения
поверхностей. Теорема Монжа. Если
две поверхности второго порядка описаны
около третьей или вписаны в нее, то линия
их пересечения распадается на две
плоские кривые второго порядка. Плоскости
этих кривых проходят через прямую,
соединяющую точки линий касания.
Рисунок 5.


а)
б)

Рисунок 5. Особый случай пересечения
поверхностей.

а) Наглядное изображение. б) Эпюр.

Рассмотрим случай пересечения поверхностей
вращения, ни одна из которых не является
проецирующей. В этом случае линия
пересечения строиться на обеих плоскостях
проекций (рис. 6).

Построение линии пересечения выполняется
в следующем порядке:

  1. Анализируем взаимное положение и форму
    поверхностей.

  2. Определяем положение основных и
    вспомогательных точек методом секущих
    плоскостей.

  3. Соединяем полученные точки.

Разберем подробно второй пункт. Точки
верха (1) и точка низа кривой (4) располагаются
на пересечении главных меридианов
(очерковых образующих) сферы и конуса,
так как их оси вращения лежат в одной
плоскости, параллельной П2. и через
них можно провести вспомогательную
секущую плоскость.

Между точками 1 и 4 будут располагаться
основные и вспомогательные точки.
Проведем вспомогательную секущую
плоскость перпендикулярно оси вращения
конуса на уровне экватора сферы, для
того чтобы определить положение основных
точек (3), которые на горизонтальной
проекции определят границу видимости,
а на фронтальной плоскости проекций
они будут совпадать ввиду симметрии
линии пересечения.

Данная вспомогательная секущая плоскость
II пересекает конус
по окружности соответствующего радиуса,
сферу также по окружности. Построим эти
окружности на горизонтальной плоскости
проекций. На пересечении этих окружностей
(сечений) получаются горизонтальные
проекции искомых точек 3. Теперь необходимо
построить их фронтальные проекции,
спроецировав на секущую плоскость.

Для уточнения формы кривой воспользуемся
вспомогательными точками (2). Для этого
проведем вспомогательную секущую I
плоскость между точкой 1 и экватором
сферы.

Проведение секущей плоскости III
ниже точки 4 не имеет смысла, так
как в этой плоскости сфера и конус не
будут иметь общих точек.

Теперь можно соединить полученные точки
с учетом видимости на горизонтальной
проекции.

Рисунок 6. Построение линии пересечения
конуса и сферы.

Источник

Выкройка для конуса

Эскизы конусов и выкроек для нихВместо слова «выкройка» иногда употребляют «развертка», однако этот термин неоднозначен: например, разверткой называют инструмент для увеличения диаметра отверстия, и в электронной технике существует понятие развертки. Поэтому, хоть я и обязан употребить слова «развертка конуса», чтобы поисковики и по ним находили эту статью, но пользоваться буду словом «выкройка».

Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).

1. Полный конус

Обозначения:

  • D — диаметр основания конуса;
  • H — высота конуса;
  • R — радиус дуги выкройки;
  • alpha — центральный угол выкройки.

Параметры выкройки рассчитываются по формулам:
R~=~k~*~{D/2};
alpha~=360/k;
где k~=~sqrt{1~+~(2*H/D)^2}.

2. Усеченный конус

Обозначения:

  • D_1 — диаметр большего основания конуса;
  • D_2 — диаметр меньшего основания конуса;
  • H — высота конуса;
  • R_1 — радиус внешней дуги выкройки;
  • R_2 — радиус внутренней дуги выкройки;
  • alpha — центральный угол выкройки.

Формулы для вычисления параметров выкройки:
R_1~=~k~*~{D_1/2};
R_2~=~k~*~{D_2/2};
alpha~=360/k;
где k~=~sqrt{1~+~(2*H/{D_1-D_2})^2}.
Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них D_2~=~0.

3. Угол при вершине конуса

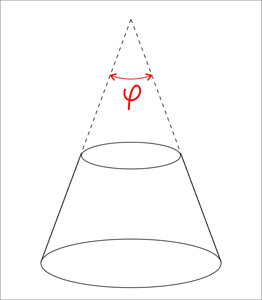
Угол при вершине конусаИногда при построении конуса принципиальным является значение угла при его вершине (или при мнимой вершине, если конус усеченный). Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой varphi (см. картинку).
В этом случае мы можем его использовать вместо одного из трех входных значений: D_1, D_2 или H. Почему «вместо«, а не «вместе«? Потому что для построения конуса достаточно трех параметров, а значение четвертого вычисляется через значения трех остальных. Почему именно трех, а не двух и не четырех — вопрос, выходящий за рамки этой статьи. Таинственный голос мне подсказывает, что это как-то связано с трехмерностью объекта «конус». (Сравните с двумя исходными параметрами двухмерного объекта «сегмент круга», по которым мы вычисляли все остальные его параметры в статье Геометрия круга.)

Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.

4. Методы построения выкройки

  • Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
  • Занести формулы и исходные данные в электронную таблицу (например, Microsoft Excel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
  • использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.

5. Не параллельные основания

Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания.
Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта:
Усеченный конус с не параллельными основаниями.

Источник

Добавить комментарий