Цепь резистор конденсатор как найти ток

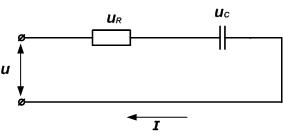
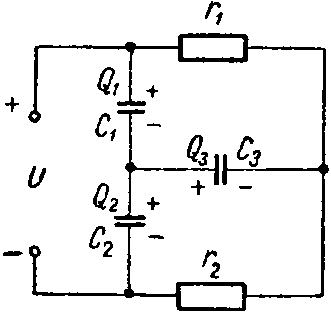
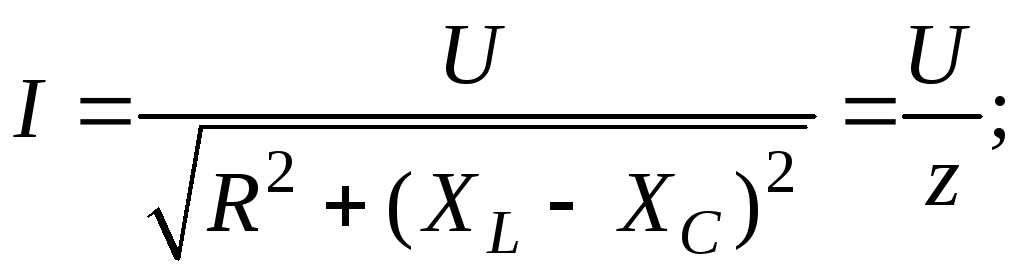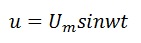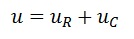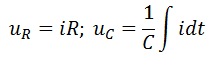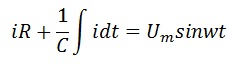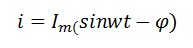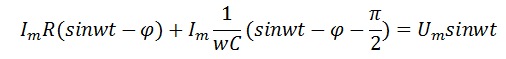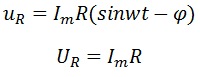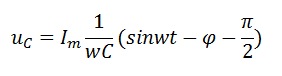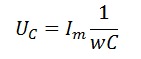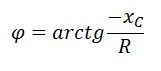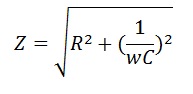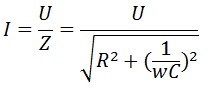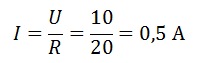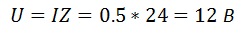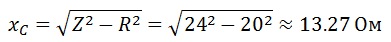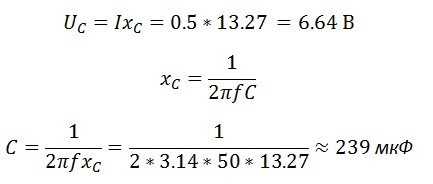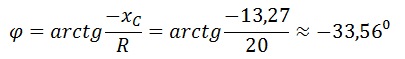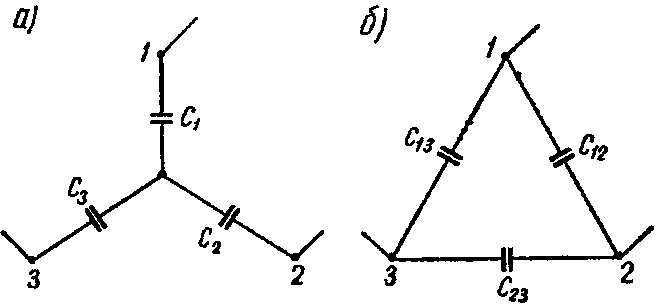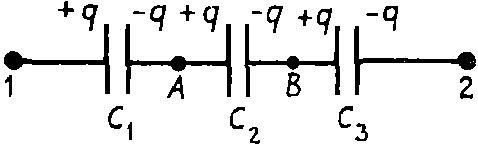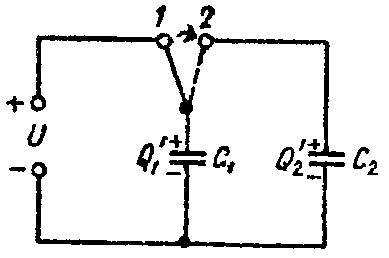Напряжение на входе цепи (рис. 2.10 а)
согласно второму закону Кирхгофа для
действующих значений определяется по
уравнению

.
(2.24)

Рис. 2.10

Построим векторную
диаграмму, полагая, что в цепи протекает
ток
и< 0. Вектор тока откладываем под угломк осив отрица­тельном направлении – по
часовой стрелке (рис. 2.10 б). Вектор
напряжения на резисторесовпадает по фазе с вектором тока, а
вектор напряжения на конденса­тореотстает от вектора тока на 90°. При
сложении двух векторов со­гласно
уравнению (2.24) получим вектор напряжения
источника(рис. 2.10 б). Из векторной диаграммы

,
(2.25)

где
– полное сопротивление цепи.

Вектор напряжения источника отстает
от вектора тока на угол
,
поэтому говорят, что цепь носит емкостный
характер (– 90°<<0).

Для треугольника напряжений (рис. 2.10
б) и треугольника сопротивлений (рис.
2.10 в) можно записать соотношения,
аналогичные (2.20), (2.21) и (2.23).

2.3.3. Последовательное соединение резистора, катушки и конденсатора

При протекании
синусоидального токапо цепи, состоящей из последовательно
соединенных элементов(рис.
2.11 а), на ее зажимах создается синусоидальное
напряжение, равное алгебраиче­ской
сумме синусоидальных напряжений на
отдельных элементах (второй за­кон
Кирхгофа):

.

Для действующих значений это уравнение
имеет вид

.

Построим векторную диаграмму с учетом
известных фазовых соотношений (рис.
2.11 б). Вектор напряжения на резисторе
совпадает по фазе с вектором тока, на
конденсаторе он отстает от вектора тока
на 90°, а на катушке опережает вектор
тока на 90°. Сумма этих векторов напряжения
на элементах цепи, даст вектор напряжения
источника.

а)	б)	в)

Рис. 2.11

Из векторной диаграммы определяем
входное напряжение

откуда ток и полное сопротивление

,
(2.26)

где
– разность индуктивного и емкостного
сопротивлений, называе­мая реактивным
сопротивлением.

Сдвиг фаз определим из треугольника
напряжений или сопротивлений:

.

Если
,
т.е.>
0, то цепь имеетиндуктивный
характер. В
этом слу­чае
(рис. 2.11 б), а сдвиг фаз> 0. Если,
т.е.<
0, то цепь имеетемкостный
характер и
сдвиг фаз
< 0 (рис. 2.11 в). Таким образом, реактивное
сопротивлениеможет быть положительным (> 0) и отрицательным (< 0).

Особый случай цепи,
когда
,
т.е. реактивное сопротивление.
В этом случае цепь имеет чисто активный
характер, а сдвиг фаз= 0. Такой режим называетсярезонансом
напряжений.

Условием резонанса напряжений является

_.

Эти условия показывает, что резонанс
напряжений в цепи можно получитьизменением частоты напряжения ис­точника,
или индуктивности катушки или емкости
конденсатора.

Угловая частота, при
которой в цепи наступает резонанс
напряжений, называетсярезо­нансной
угловой частотой

Полное сопротивление цепи минимальное
и равно активному

Ток в цепи, очевидно,
будет максимальным

Напряжение на резисторе равно напряжению
источника:
.

Резонанс
напряжений, как правило, нежелателен в
электроэнергетике, но широко применяется
в радиотехниче­ских устройствах,
автоматике, телемеханике, связи,
измерительной технике и др..

Соседние файлы в папке Лекции

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Рассмотрим последовательную RC-цепь, состоящую из последовательно соединенных резистора и конденсатора.

Напряжение на зажимах цепи

По второму закону Кирхгофа это же напряжение можно определить как сумму падений напряжений на резисторе и конденсаторе

где

Тогда первое выражение можно переписать в следующем виде

Ток в цепи равен

Подставив в выражение выше, и выполнив интегрирование, получим

Напряжение на резисторе равно

Напряжение на конденсаторе

Как видно из последнего выражения напряжение на конденсаторе отстает от тока на угол π/2.

Реактивное (емкостное) сопротивление конденсатора равно

С уменьшением частоты емкостное сопротивление конденсатора увеличивается. При постоянном токе оно равно бесконечности, так как частота равна нулю.

Сдвиг фаз в последовательной RC – цепи можно определить по формуле

Полное сопротивление RC-цепи

Амплитудное значение тока

Рассмотрим пример решения задачи с RC-цепью

Полное сопротивление последовательной RC– цепи равно 24 Ом. Напряжение на резисторе равно 10 В, а его сопротивление 20 Ом. Найдите С, Uc, U, I, сдвиг фаз φ. Постройте векторную диаграмму.

Найдем ток, протекающий через резистор. Так как соединение последовательное, то этот ток будет общим для всей цепи.

Зная ток и сопротивление цепи, найдем напряжение

Емкостное сопротивление конденсатора

Зная сопротивление, найдем напряжение и емкость

Сдвиг фаз

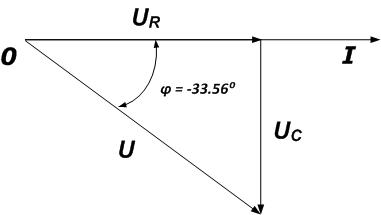
Построим векторную диаграмму RC – цепи, при этом учитываем, что напряжение на конденсаторе отстает от тока (это видно по знаку сдвига фаз).

Сначала откладывается вектор тока в цепи, затем напряжение на резисторе и напряжение на конденсаторе. Затем строится вектор общего напряжения как сумма векторов напряжений на конденсаторе и на резисторе.

Читайте также – Последовательная RL-цепь

Просмотров: 34891

Электрическая цепь RC

Рассмотрим ток в электрической цепи, состоящей из конденсатора ёмкостью C и резистора сопротивлением R, соединённых параллельно.
Значение тока заряда или разряда конденсатора определится выражением I = C(dU/dt), а значение тока в резисторе,
согласно закону Ома, составит U/R, где U – напряжение заряда конденсатора.

Из рисунка видно, что электрический ток I в элементах C и R цепи будет иметь одинаковое значение и
противоположное направление, согласно закону Кирхгофа. Следовательно, его можно выразить следующим образом:

Решаем дифференциальное уравнение C(dU/dt)= -U/R

Интегрируем:

Из таблицы интегралов здесь используем преобразование

Получаем общий интеграл уравнения: ln|U| = – t/RC + Const.
Выразим из него напряжение U потенцированием: U = e^-t/RC * e^Const.
Решение примет вид:

U = e^-t/RC * Const.

Здесь Const – константа, величина, определяемая начальными условиями.

Следовательно, напряжение U заряда или разряда конденсатора будет меняться во времени по экспоненциальному закону
e^-t/RC.

Экспонента – функция exp(x) = e^x
e – Математическая константа, приблизительно равная 2.718281828…

---

Постоянная времени τ

Если конденсатор емкостью C последовательно с резистором сопротивлением R подключить к источнику постоянного напряжения U,
в цепи пойдёт ток, который за любое время t зарядит конденсатор до значения U_C и определится выражением:

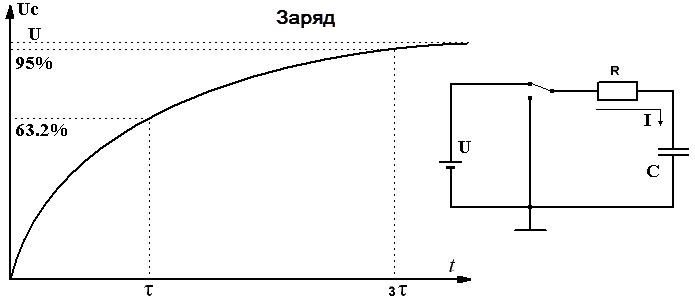
Тогда напряжение U_C на выводах конденсатора будет увеличиваться от нуля до значения U по экспоненте:

U_C = U(1 – e^-t/RC)

При t = RC, напряжение на конденсаторе составит U_C = U(1 – e^-1) = U(1 – 1/e) .
Время, численно равное произведению RC, называется постоянной времени цепи RC и обозначается греческой буквой τ.

Постоянная времени τ = RC

За время τ конденсатор зарядится до (1 – 1/e)*100% ≈ 63,2% значения U.
За время 3τ напряжение составит (1 – 1/e³)*100% ≈ 95% значения U.
За время 5τ напряжение возрастёт до (1 – 1/e⁵)*100% ≈ 99% значения U.

---

Если к конденсатору емкостью C, заряженному до напряжения U, параллельно подключить резистор сопротивлением R,
тогда в цепи пойдёт ток разряда конденсатора.

Напряжение на конденсаторе при разряде будет составлять U_C = Ue^-t/τ = U/e^t/τ.

За время τ напряжение на конденсаторе уменьшится до значения U/e, что составит 1/e*100% ≈ 36.8% значения U.

За время 3τ конденсатор разрядится до (1/e³)*100% ≈ 5% от значения U.
За время 5τ до (1/e⁵)*100% ≈ 1% значения U.

Параметр τ широко применяется при расчётах RC-фильтров различных электронных цепей и узлов.

---

Пример 4.5. Последовательное соединение резистора и конденсатора в цепи синусоидального тока.

К цепи с последовательным соединением активного сопротивления

R = 12 Ом и емкостного Х_с = 16 Ом подведено общее напряжение u_об =170sinwt, В. Определить ток в цепи, активную, реактивную и полную мощности, построить векторную диаграмму.

Полное сопротивление цепи .

По закону Ома находим ток в цепи:

Символ квадратного кореня из двух появился в формуле чтобы перевести амплитудное значение напряжения в действующее.

Мощности, выделяющиеся в цепи:

активная Р = I 2 ·R=36 ·12 = 432 Вт,

реактивная Q_С = I 2 ·X_{C =} 6 2 ·16 = 576 Вар,

полная S =UI = 120·6 = 720 ВА.

При построении диаграммы, прежде всего, строим вектор тока I, поскольку он одинаков для всех элементов последовательной цепи. Активное напряжение U_a совпадает по фазе с током, ёмкостное – U_С отстаёт от тока на угол 90 градусов. (Учитывая, что вектора на диаграммах вращаются против часовой стрелки, направляем вектор напряжения U_С вниз.) Общее напряжение U_об равно векторной сумме напряжений U_a и U_С. Этот вектор проводится из начала вектора U_a в конец вектора U_С.

Пример 4.6. Цепь с последовательным соединением резистора, индуктивности и конденсатора.

Неразветвлённая цепь содержит последовательно включённые сопротивления: R=4 Ом, X_L = 7 Ом и X_C = 10 Ом. Напряжение на зажимах цепи U_об = 24 В. Определить ток, реактивную мощность цепи, напряжение на резисторе и на индуктивности, а также показания вольтметра. Построить векторную диаграмму.

Полное сопротивление цепи

Ток в цепи, по закону Ома:

I = U/Z == 24/5 = 4,8 А.

Напряжение на резисторе:

U_R=IR=4,8 · 4=19,2 В.

Напряжение на индуктивности:

U_L=I·X_L=4,8·7=33,6 В.

Вольтметр подключён так, что показывает суммарное напряжение на R и L. Как известно, в цепях переменного тока нельзя складывать величины арифметически. В соответствии с векторной диаграммой для данной цепи, по теореме Пифагора:

U_{вольтметра}=

Построение векторной диаграммы начинается с вектора тока. Затем последовательно, в виде цепочки векторов, строятся вектора напряжений на элементах цепи: U_а, U_L, U_С, Uоб. Прежде всего, отображается вектор активного напряжения U_а, которое совпадает с током по фазе. Затем строится вектор напряжения U_L, опережающий ток по фазе на 90 градусов. После этого откладывается вектор напряжения U_С, который отстаёт по фазе от тока на 90 градусов. Последним строится вектор общего напряжения Uоб. Его проводят от начала вектора U_а к концу вектора U_С.

Общее напряжение U_об равно векторной сумме напряжений U_а, U_L и U_С.

Реактивная мощность: Q_С = I 2 (X_L-X_C) = 4,8 2 (7-10) = — 69,1 Вар. (Реактивная мощность получилась отрицательной, что указывает на то, что она имеет ёмкостный характер.)

Пример 4.7 Резонанс напряжений.

Цепь с последовательным соединением активного сопротивления R, индуктивности L и емкости C настроена на резонанс напряжений. При этом сопротивления элементов цепи: R = 3 Ом, X_L,=Xc= 15 Ом. Напряжение на входе цепи U_об = 24 В. Определить ток в цепи, индуктивное напряжение U_L, активную мощность Р и реактивную мощность Q_об, выделяющуюся в цепи.

Полное сопротивление цепи Z при резонансе напряжений равно активному R=3 Ом, а ток в цепи

I = U / z = 24/3 = 8 А.

Напряжение на индуктивности U_L =I · X_L= 8 ·15= 120 В. (Заметьте, что напряжение на реактивном элементе получилось много больше напряжения U_об на входе всей цепи.)

Активная мощность, выделяющаяся в цепи:

Р = UI = 24 • 8 = 192 Вт.

Реактивная мощность Q_об, выделяющаяся в цепи, равна нулю, т.к. при резонансе цепь ведёт себя как чисто активное сопротивление. (Реактивные мощности Q_L и Q_C , выделяющиеся в реактивных элементах цепи равны по величине и противоположны по знаку.) Следовательно, при резонансе общая мощность цепи S равна активной мощности Р.

Пример 4. 8. Расчёт простейшей разветвлённой цепи.

Общий ток I в неразветвленной части цепи переменного тока составляет 1 А при напряжении на зажимах цепи 60 В. Коэффициент мощности цепи cosφ=0,6.

Определить активную I_а и емкостную составляющие I_с тока, активное сопротивление, емкость конденсатора C, если частота тока f составляет 50 Гц. Построить векторную диаграмму для данной схемы.

Построим векторную диаграмму для цепи. Построение начинаем с вектора напряжения U, поскольку оно является одинаковым для обеих ветвей цепи. Вектор тока в резисторе I_a совпадает по фазе с напряжением. К концу вектора I_a пристраиваем вектор тока в конденсаторе I_с . Этот вектор направлен вниз, поскольку ток в конденсаторе отстаёт по фазе от напряжения на угол 90 градусов.

Вектор общего тока I_об проводим из начала первого в конец последнего вектора. Ток I_об является суммой токов в ветвях.

Зная коэффициент мощности цепии величину тока I_об, находим величину токов в ветвях:

I_a= I_об·cosj = 1· 0,6 = 0,6A;

Значение sinj найдено по значению cosj.

Теперь можно найти величину сопротивления:

R = U / I_a = 60 / 0,6 = 100 Ом.

Из формулы ёмкостного сопротивления X_c = 1 / 2p·f·C найдём величину ёмкости конденсатора:

С = 1 / 2p·f·X_c = 1 / 2·3,14·50·75 =0,0000425 Ф = 42,5 мкФ.

Пример 4. 9. Расчёт цепи переменного тока с параллельным соединением ветвей без использования метода проводимости.

Приборы, включенные в цепь переменного тока, показывают: амперметры (A1 и А2) — 10 А, вольтметр — 220 В, ваттметр — 3520 Вт. Определить ток всей цепи и угол сдвига фаз тока I относительно напряжения U.

Перед началом решения задачи проанализируем схему. В левой ветви схемы (в неё входит резистор R₁) протекает ток I₁ активного характера, т. к. в ветви включено только активное сопротивление. В правой ветви (она состоит из последовательно включённых элементов: резистора R₂ и индуктивности L) протекает ток I₂ активно-индуктивного характера. Величину токов в ветвях показывают амперметры.

Вольтметр показывает напряжение на входе цепи. Ваттметр показывает активную мощность, потребляемую всей цепью. Общий ток равен векторной сумме токов в ветвях.

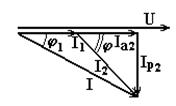
На основании проведённого анализа построим векторную диаграмму для данной цепи. Сначала построим вектор напряжения на входе цепи U. Затем строим активный ток в левой ветви I₁ и активную составляющую тока в правой ветви I_a2, совпадающие по фазе с напряжением на входе цепи. Реактивная (индуктивная) составляющая тока I_p2 в правой ветви отстаёт по фазе от напряжения на угол 90 градусов. Общий ток равен сумме векторов I₁ + I_a2 + I_p2.

Активная составляющая тока всей цепи I_a слагается из двух составляющих I₁ + I_a2 = P/U = 3520 / 220 = 16 А.

Активная составляющая второго тока I_{a2_} = I_a — I₁ = 16 — 10 = 6 А. Реактивная составляющая второго тока I_p2=

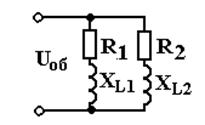
Пример 4. 10. Расчёт цепи переменного тока при параллельном соединении ветвей методом проводимости

Две катушки индуктивности соединены параллельно и имеют сопротивления: r₁= 6 Ом,

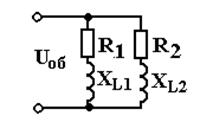
x_L1=8 Ом; r₂ = 8 Ом; x_L2 = 6 Ом. Напряжение источника энергии U = 220 В.

Определить токи в ветвях, ток в неразветвленной части цепи и активную мощность Р. Построить диаграмму проводимостей.

Определим проводимости ветвей и общую проводимость всей цепи.

Активная проводимость левой ветви: g₁=r₁/z₁ 2 =6/ (6 2 +8 2 ) =6 ·10 -2 Cм.

Активная проводимость правой ветви: g₂=r₂/z₂ 2 =8/(8 2 +6 2 ) = 8·10 -2 Cм.

Реактивная проводимость левой ветви: b₁= x₁/z₁ 2 =8/ (6 2 +8 2 ) =8 ·10 -2 Cм

Реактивная проводимость правой ветви: b₂=x₂/z₂ 2 =6/(8 2 +6 2 ) = 6·10 -2 Cм.

Чтобы найти общий ток в неразветвлённой части цепи построим диаграмму проводимостей.

Из рассмотрения диаграммы становится понятным принцип вычисления полной проводимости всей цепи по известным проводимостям ветвей. (В большом треугольнике горизонтальный катет равен сумме активных проводимостей, а вертикальный — сумме реактивных проводимостей. По теореме Пифагора находим гипотенузу треугольника, которая изображает полную проводимость всей цепи.)

Общая проводимость цепи:

Ток в неразветвлённой части цепи I =U·Y=220·19,7·10 -2 =43,3A.

Пример 4.11. Расчёт цепи с конденсатором с использованием метода комплексных чисел

К конденсатору С2, обладающему ёмкостным сопротивлением x_С2= 6 Ом, приложено напряжение U₂= 300e В. Найти ток в цепи.

Решение:

Прежде всего выражаем сопротивление конденсатора в комплексной форме:

Затем, по закону Ома, находим ток в цепи:

I₂= U₂ / Z₂ = 300e / 6e = 50e А.

Пример 4.12. Расчёт последовательной цепи с использованием комплексных чисел.

К цепи с последовательным сопротивлением элементов r₃= 10 Ом и X_L3 = 8 Ом подключено напряжение U₃= 300e В.

Найти ток в цепи и напряжение на каждом элементе.

Сначала находим комплексное сопротивление цепи:

Теперь можно найти ток в цепи по закону Ома:

I₃ = U₃ / Z₃ = U₃= 300e / 12,8e = 23,8 А.

Теперь найдем напряжение на резисторе

и на индуктивном сопротивлении

Задача 20

Определить показания вольтметра, если известны параметры цепи: Uобщ = 100 В, R = 30 Ом, Х_L = 90 Ом, Хс = 50 Ом.

Постройте в масштабе векторную диаграмму для тока и напряжений.

Ответ: показания вольтметра 100В

В электрической цепи протекает ток I = 5 A, частота приложенного к цепи напряжения f = 50 Гц. Напряжения на элементах цепи составляют: U₁ = 50 B, U₂ = 100 B, U₃ = 60 B.

Определите напряжения на элементах этой цепи, если, при том же напряжении U на входе цепи, частота возрастёт до 100 Гц?

Постройте в масштабе векторную диаграмму для тока и напряжений при частоте 50 герц.

Определить величину активного сопротивления R, а также индуктивного сопротивления X_C, если ко входу цепи приложено напряжение U = 200 B, ваттметр показывает активную мощность 640 Вт, а амперметр — ток 4 А.

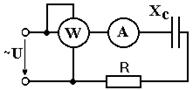
Постройте в масштабе векторную диаграмму для тока и напряжений.

Ответ: R= 40 Ом; X_С = 30 Ом

Задача 23

Определить сопротивления резистора R и конденсатора X_C, если приборы в цепи показывают: мощность Р = 90 Вт, ток всей цепи I­₁ = 5 A, ток через конденсатор I₂ = 4 A.

Постройте в масштабе векторную диаграмму для тока и напряжений.

Ответ : R = 10 Ом ; X_C = 7,5 Ом .

К схеме приложено переменное напряжение, частотой f = 50 Гц. В схеме протекает ток I = 5 A. При этом на резисторе действует напряжение U₁ = 50 B, на катушке индуктивности U₂ = 100 B, а на конденсаторе U₃ = 60 B.

Определите, при какой частоте приложенного напряжения в схеме возникнет резонанс напряжений.Каким будет ток в цепи, если величина входного напряжения не изменится?

Ответ: резонанс возникнет при частоте 40 Гц, ток в цепи при резонансе составит 6,4 А.

Задача 2 5

Определить сопротивление R и активную мощность Р цепи, если X_L = 30 Ом, амперметр

показывает 4 А, вольтметр 200 В.

Постройте в масштабе векторную диаграмму для напряжения и токов.

Ответ: R = 40 Ом, Р = 640 Вт.

Задача 26*

Определите активную мощность цепи. Необходимые для расчёта данные возьмите с рисунка.

Ответ: 1. 1480 Вт.

Определить напряжение U на входе цепи, общий ток цепи I, напряжение на горизонтальной ветви U₁, напряжение на индуктивности U₂, и напряжение U­_3, на цепочке, состоящей из элементов L и C.

Известно, что: X_L = X_C = R = 5 Ом, I₃ = 10 A.

Ответы : I = 20 A; U₁ = 141B; U₂ = 50 B;

Задача 28

Цепь переменного тока с последовательным соединением активного сопротивления, индуктивности и емкости настроена на резонанс напряжений. При этом активное сопротивление R = 3 Ом, индуктивное сопротивление X_L равно ёмкостному сопротивлению X_Си составляют 20 Ом каждое.

Напряжение на входе цепи U_об = 12 В. Определить ток в цепи и напряжение U_L на индуктивности. Найти активную и реактивную мощности, выделяющиеся в цепи.

Построить векторную диаграмму без масштаба. Определить величину индуктивности L и ёмкости С, если резонанс возник на частоте 250 Гц.

Задача 29

Две катушки индуктивности соединены параллельно и имеют сопротивления: R₁= 6 Ом, X_L1=8 Ом; R₂ = 16 Ом; X_L2 = 12 Ом. Напряжение источника энергии U = 220 В.

Найти токи в ветвях и общий ток двумя разными способами: а) путём построения в масштабе векторной диаграммы; б) используя метод комплексных чисел.

Задача 30

К цепи с последовательным соединением активного сопротивления R = 12 Ом и индуктивности 314мГн подведено общее напряжение U =120 вольт. Определить действующее значение тока в цепи, активную, реактивную и полную мощности, построить векторную диаграмму без масштаба.

Задача 31

В сеть переменного тока с действующим напряжением 220 В включены последовательно конденсатор емкостью 100 мкФ, катушка индуктивностью 0,4 Гн и активное сопротивление 8 Ом. Определите амплитуду силы тока в цепи, если частота переменного тока 200 Гц. Найдите также частоту переменного тока, при которой в данной схеме наступит резонанс напряжений.

Ответы: ток в цепи при резонансе 0,43А; частота, при которой возникает резонанс 25 Гц.

5. Цепи трёхфазного тока

Решение задач на трехфазный ток требует знания свойств соединения потребителей звездой и треугольником, умения строить векторные диаграммы для указанного соединения.

Источник

Последовательная RC-цепь

Рассмотрим последовательную RC-цепь, состоящую из последовательно соединенных резистора и конденсатора.

Напряжение на зажимах цепи

По второму закону Кирхгофа это же напряжение можно определить как сумму падений напряжений на резисторе и конденсаторе

Тогда первое выражение можно переписать в следующем виде

Ток в цепи равен

Подставив в выражение выше, и выполнив интегрирование, получим

Напряжение на резисторе равно

Напряжение на конденсаторе

Как видно из последнего выражения напряжение на конденсаторе отстает от тока на угол π/2.

Реактивное (емкостное) сопротивление конденсатора равно

С уменьшением частоты емкостное сопротивление конденсатора увеличивается. При постоянном токе оно равно бесконечности, так как частота равна нулю.

Сдвиг фаз в последовательной RC – цепи можно определить по формуле

Полное сопротивление RC-цепи

Рассмотрим пример решения задачи с RC-цепью

Полное сопротивление последовательной RC— цепи равно 24 Ом. Напряжение на резисторе равно 10 В, а его сопротивление 20 Ом. Найдите С, Uc, U, I, сдвиг фаз φ. Постройте векторную диаграмму.

Найдем ток, протекающий через резистор. Так как соединение последовательное, то этот ток будет общим для всей цепи.

Зная ток и сопротивление цепи, найдем напряжение

Емкостное сопротивление конденсатора

Зная сопротивление, найдем напряжение и емкость

Построим векторную диаграмму RC – цепи, при этом учитываем, что напряжение на конденсаторе отстает от тока (это видно по знаку сдвига фаз).

Сначала откладывается вектор тока в цепи, затем напряжение на резисторе и напряжение на конденсаторе. Затем строится вектор общего напряжения как сумма векторов напряжений на конденсаторе и на резисторе.

Источник

Параллельное соединение резистора и конденсатора

Компоненты электрической цепи

Для чего предназначены резисторы и конденсаторы

Резисторы – одни из наиболее распространённых элементов в электронике. Их главное назначение – сопротивление течению тока и преобразовывать его в тепло. Главной характеристикой данных элементов является значение R.

Чем больше величина R, тем большая часть электроэнергии сможет рассеется в тепло. В схемах, которые питаются небольшим напряжением от 5 до 12 В, чаще всего используют резисторы имеющие величину R от 100 Ом до 100 кОм.

Конденсаторы – устройства, главная задача которых накапливать электрические заряды. Стоит отметить, что эту же функцию выполняет и аккумулятор, но в отличие от батареи конденсатор сразу же отдаёт весь накопившийся заряд. Величина, которую способно накопить устройство, называют «ёмкость».

Когда подсоединяется цепь к источнику электроэнергии: через конденсатор течет электрический ток. Сила тока в начале прохождения через устройство имеет наивысшее значение, в это же время напряжение станет низким.

После того, как устройство начнет накопление заряда, сила тока упадёт до нуля, а напряжение наоборот станет увеличиваться.

Особенности соединения резистора и конденсатора в цепи

Существует два типа соединения резисторов и конденсаторов: параллельное и последовательное.

Параллельное соединение резистора и конденсатора

Для того, чтобы осуществить параллельное соединение резистора и конденсатора, необходимо объединить все элементы цепи двумя узлами. Они не должны иметь связи с другими элементами.

При таком соединении, величина напряжения между обоими узлами станет падать, и оно станет равным для каждого элемента. А величина, которая обратна общему R, будет равняться сумме величин, которые обратны R всех проводников.

Когда осуществляется параллельное соединение резисторов, проводимость всех резисторов станет равняться проводимости цепи.

Если резистор соединить к заряженному конденсатору то вполне возможно короткое замыкание.

Последовательное соединение

Последовательное соединение – связка элементов между собой так, чтобы начальный участок цепи не имел ни одного узла. При таком соединении величина тока на проводниках станет равна между собой.

Когда осуществляется последовательное соединение всех элементов, то их общая ёмкость имеет формулу 1/С_общ = 1/С₁ + 1/С₂ + … + 1/С_n.

Как рассчитать импеданс в цепи

Импеданс – полное R тока, который обозначается Z. Этот параметр – отражение меняющегося во времени значения тока. Импеданс – векторная величина, которая состоит из двух значений: активное и реактивное сопротивление.

Активная часть импеданса, которая обозначается R – это мера степени, с которой материал будет противостоять движению электронов между атомными частицами. Чем легче атомные частицы освобождают или принимают электроны, тем ниже и сопротивление.

К материалам с минимальным сопротивлением можно отнести сталь, алюминий, золото. Самое большое значение R имеют стекло, слюда, полиэтилен и чаще всего их называют изоляторы или диэлектрики.

Стоит отметить! Активное R, имеет одно и тоже значение, как при последовательном, так и при параллельном соединении.

Если использовать резисторы в цепях синусоидального тока, то термин «импеданс» будет использоваться для обозначения сопротивления R=Z.

Практические расчеты импеданса чаще всего выполняются по следующей формуле:

Реактивное сопротивление обозначается X и является выражением степени, с которой электронный компонент схемы станет хранить или высвобождать электроэнергию, в то время, когда сила тока и значение напряжения станет колебаться при каждом цикле. Реактивное сопротивление выражается в числе Ом.

Энергия будет храниться и выделяться в двух типах:

• Магнитного поля. Реактивная часть является индуктивной.
• Электрического поля.

Как рассчитать время разряда и заряда конденсатора через резистор

Чтобы осуществить заряд устройства, нужно включить устройство в цепь и присоединить к зажимам генератора. Как вы уже знаете, генератор имеет внутреннее сопротивление.

Если резистор подключить к заряженному конденсатору то ключ будет замкнут и конденсатор начнёт зарядку до напряжения между обкладками, которая станет равна э.д.с генератора и равна Uc=E. При этом, обкладка которая соединена с положительным зажимом, получит положительный заряд, вторая же получит отрицательный заряд.

Чтобы обе обкладки устройства полностью зарядились, нужно, чтобы одни из них приобрела определенное количество электронов, а вторая столько же потеряла.

Зарядный ток в цепи будет протекать сотые доли секунды, пока величина напряжения на устройстве достигнет такой же уровня, что и на генераторе. В то время, пока конденсатор будет заряжаться, по всей цепи будет проходить зарядный ток. Вначале он будет иметь максимальную величину, т.к. величина напряжения станет равна 0.

По мере того как конденсатор станет заряжаться, величина R на нём будет падать.

Время процесса зарядки будет зависеть от следующих величин:

1. Внутреннее сопротивление электрического генератора.
2. Способность конденсатора принять количество тока.

Для того, чтобы разрядить устройство нужно отключить его от генератора переменного тока и присоединить к его обкладкам сопротивление. Дело в том, что на обкладках уже есть разность потенциалов, поэтому в цепи потечет ток.

Он будет проходить от одной обкладки через сопротивление к другой. Процесс разряда будет проходить до тех пор, пока обе обкладки не станут равны, т.е. пока напряжение между ними станет равно 0.

В самом начале, напряжение будет максимальным, сила тока – наибольшая. Как только начнется разрядка, напряжение и сила тока будут уменьшаться.

Продолжительность разряда устройства имеет зависимость от:

• Отношению заряда к разности потенциалов;
• Удельному электрическому сопротивлению.

Чем значение сопротивления выше, тем дольше будет происходить разряд конденсатора. Это можно объяснить тем, что при максимальном сопротивлении, сила тока небольшая, а величина заряда станет медленно уменьшаться.

Важно! Заряженный конденсатор не станет пропускать постоянный ток, потому что диэлектрик между его положительной и отрицательной обкладками будет размыкать цепь.

Для того, чтобы рассчитать время заряда и разряда на устройстве, лучше всего воспользоваться онлайн калькулятором.

Источник

Электрик в доме

Рубрики

Свежие записи

Свежие комментарии

Расчёт сопротивления резисторов и ёмкости конденсаторов

Автор: admin, 22 Мар 2013

Расчёт сопротивления резисторов и ёмкости конденсаторов

В этой статье рассмотрим как можно с помощью параллельного и последовательного включения резисторов и конденсаторов подобрать нужный номинал радиодетали, при отсутствии нужного. Расчёт производится по формулам расчёта сопротивления и ёмкости для параллельного и последовательного включения, а также с помощью удобной таблицы подбора ёмкости и сопротивления.

Резисторы

Широко применяются в радиоприёмниках, усилителях сигналов и во многих других схемах. Они служат для ограничения тока, создания падения напряжения, регулирования частоты, громкости и других сигналов. Обозначаются на схемах буквой R. Сопротивление резистора измеряется в Омах. Для больших сопротивлений используют единицы: килоомы (1кОм=1000Ом), мегаомы (1Мом=1000кОм). Кроме сопротивления резисторы характеризуются мощностью рассеяния, это такая наибольшая мощность, которую резистор может выдержать длительное время. Мощность рассеяния измеряется в ваттах (Вт). Ещё один показатель — это наибольшее возможное отклонение действительного сопротивления от номинального, указанного на резисторе, выражается в %. Резисторы бывают постоянные (не изменяют своего сопротивления) и переменные(изменяют сопротивление в зависимости от положения движка резистора).

Иногда, при сборке схемы не оказывается под рукой резистора нужного номинала. В этом случае в большинстве случаев можно заменить резистор на ближайший по номиналу — например вместо 110 Ом можно использовать резистор номиналом 100 или 120 Ом. А если нет и ближайшего по номиналу или требуется точное значение сопротивления, то можно составить нужное сопротивление с помощью последовательного или параллельного соединения нескольких резисторов.

Последовательное соединение резисторов:

последовательное соединение резисторов

При последовательном соединении резисторов их общее сопротивление равно их сумме: Rобщ = R1+R2+…+Rn.

Параллельное соединение резисторов:

параллельное соединение резисторов

При параллельном соединении резисторов их общее сопротивление рассчитывается по формуле:

1/Rобщ = 1/R1 + 1/R2 +…+1/Rn или

Rобщ = 1/(1/R1 + 1/R2 +…+1/Rn).

На практике для подбора нужного сопротивления обычно включают параллельно два резистора, в этом случае формула примет вид:

Ещё можно отметить, что при включении резисторов одинакового сопротивления, то их общее сопротивление будет равно половине сопротивления каждого их них. Мощность рассеяния, в этом случае, увеличится в 2 раза. Также при параллельном соединении общее сопротивление всегда меньше наименьшего из включенных в параллель резисторов.

Конденсаторы

Конденсаторы, как и резисторы, тоже очень широко применяются. Конденсатор это накопитель энергии, в простейшем виде это две пластины, между которыми находится диэлектрик, в качестве диэлектрика может быть просто воздух. Конденсаторы также бывают постоянной и переменной ёмкости. Единицей ёмкости является фарада(Ф). На практике используют меньшие ёмкости, их выражают в микрофарадах(1Ф=1 000 000 мкФ), нанофарадах(1мкФ = 1 000 нФ), пикофарадах(1нФ=1 000 пФ). Также конденсаторы характеризуются рабочим напряжением, выражаемом в вольтах (В). Превышение на конденсаторе напряжения выше рабочего может привести к «пробою» диэлектрика конденсатора.

Конденсатор не проводит постоянный ток, а переменному току оказывает сопротивление, которое вычисляется по формуле:

Хс = 1/(2πfC), где

• Хс — емкостное сопротивление конденсатора, Ом;
• π— математическая константа, примерно равная 3,1416;
• f — частота переменного тока, Гц;
• С — ёмкость конденсатора, Ф.

Рассмотрим как можно собрать нужную ёмкость из имеющихся под рукой.

Последовательное включение конденсаторов:

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов их общая ёмкость рассчитывается по формуле, очень похожей на формулу для параллельного включения резисторов:

Но чаще тоже используют два конденсатора, тогда формула упрощается:

Также, при включении конденсаторов с одинаковой ёмкостью их общая ёмкость будет в два раза меньше ёмкости каждого из них. Рабочее напряжение такого сборного конденсатора увеличится в 2 раза.

Параллельное включение конденсаторов:

Параллельное соединение конденсаторов

При параллельном соединении конденсаторов их общая ёмкость будет равна сумме всех емкостей.

При необходимости можно делать даже комбинированные соединения и параллельные и последовательные, в этом случае высчитывается ёмкость(или сопротивление) по одинаковым группам соединений, получают промежуточные значения, например Собщ1, Собщ2. а потом уже из них высчитывают общее значение.

Но, как правило, более двух деталей для составления нужного номинала не используют, для параллельного соединения конденсаторов и последовательного резисторов всё просто — считаем сумму. А для последовательного соединения конденсаторов и параллельного соединения резисторов нужно считать, поэтому будет удобно пользоваться заранее составленной таблицей, которая подойдёт для обоих радиоэлементов.

Таблица расчёта общего сопротивления (ёмкости) для двух параллельно соединённых резисторов (двух последовательно соединённых конденсаторов)

Таблица расчёта общего сопротивления(ёмкости)

По горизонтали смотрим значения, выделенные зелёным цветом, первого резистора(конденсатора) по вертикали второго. На перекрестии этих двух значений и будет общее сопротивление (ёмкость).

Источник

Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Основные положения и соотношения

1. Общее выражение емкости конденсатора

C= Q U .

2. Емкость плоского конденсатора

C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,

здесь

S — поверхность каждой пластины конденсатора;

d — расстояние между ними;

ε_a = ε_r·ε₀ — абсолютная диэлектрическая проницаемость среды;

ε_r — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);

ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12    Ф м  – электрическая постоянная.

3. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .

4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:

C= C 1 ⋅ C 2 C 1 + C 2 ,

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

U 1 =U⋅ C 2 C 1 + C 2 ;    U 2 =U⋅ C 1 C 1 + C 2 .

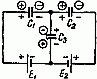
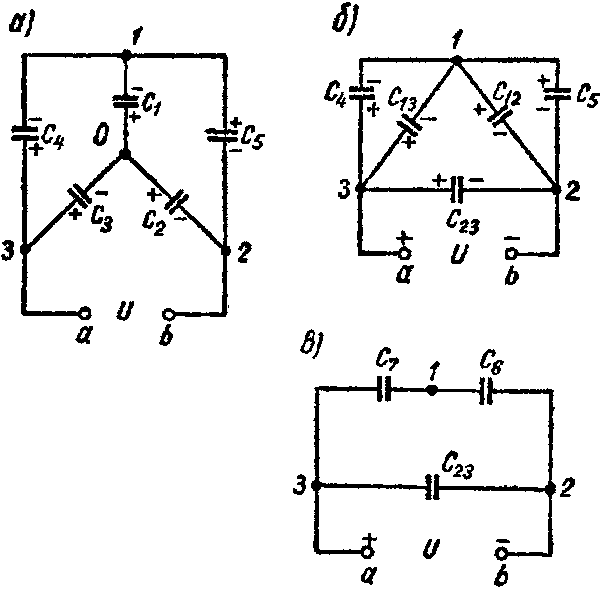
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)

Рис. 0

осуществляется по формулам:

Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ;   C 13 = C 1 ⋅ C 3 ΣC ;   C 23 = C 2 ⋅ C 3 ΣC , где          ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .

6. Энергия электростатического поля конденсатора:

W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .

7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

ΣQ=Σ Q ′ .

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .

Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.

Решение задач на расчет электрической цепи постоянного тока с конденсаторами

Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).

Рис. 1

Решение

На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U₁₂, то на левую пластину конденсатора С₁ перейдет заряд +q, на правую пластину конденсатора С₃ заряд –q.

Вследствие электризации через влияние правая пластина конденсатора С₁ будет иметь заряд –q, а так как пластины конденсаторов С₁ и С₂ соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C₂ будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.

Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.

Разность потенциалов U₁₂ = φ₁ — φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов

U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .

Воспользовавшись формулой напряжения на конденсаторе

U= q C ,

запишем

q C = q C 1 + q C 2 + q C 3 .

Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов

1 C = 1 C 1 + 1 C 2 + 1 C 3 .

В общем случае эквивалентная емкость при последовательном соединении конденсаторов

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

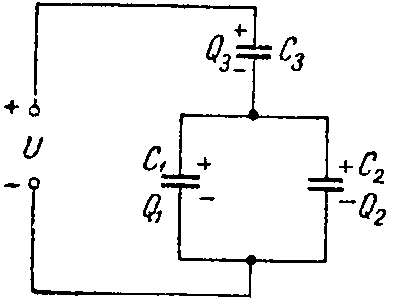
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.

Рис. 2

Емкости конденсаторов: C₁ =50 мкФ; C₂ =150 мкФ; C₃ =300 мкФ.

Решение

Эквивалентная емкость конденсаторов C₁ и C₂, соединенных параллельно

C₁₂ = C₁ + C₂ = 200 мкФ,

эквивалентная емкость всей цепи равна

C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120  мкФ.

Заряд на эквивалентной емкости

Q = C·U = 120·10^–6·240 = 288·10^–4 Кл.

Той же величине равен заряд Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288·10^–4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96  В.

Напряжение на конденсаторах C₁ и C₂ равно

U₁ = U₂ = U — U₃ = 240 — 96 = 144 В.

их заряды имеют следующие значения

Q₁ = C₁·U₁ = 50·10^–6·144 = 72·10^–4 Кл;

Q₂ = C₂·U₂ = 150·10^–6·144 = 216·10^–4 Кл.

Энергии электростатического поля конденсаторов равны

W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52  Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56  Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38  Дж.

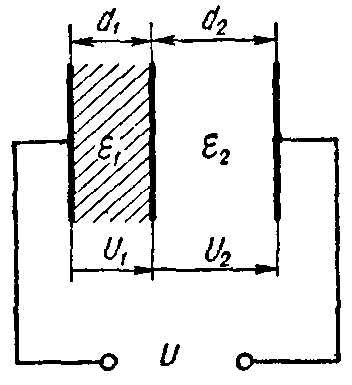
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см², имеет диэлектрик, состоящий из слюды (ε_r1 = 6) толщиною d₁ = 0,3 мм и стекла (ε_r2 = 7) толщиною d₂ =0,4 мм.

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

Рис. 3

Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Решение

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .

Подставляя сюда числовые значения, предварительно заменив ε_a1 = ε_r1·ε₀ и ε_a2 = ε_r2·ε₀, получим

C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12   Ф.

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через U_пр, при этом заряд конденсатора будет равен

Q = C·U_пр.

Напряжения на каждом слое будут равны

U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .

Напряженности электростатического поля в каждом слое

E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .

Здесь U’_np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”_np — общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5  кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0  кВ.

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

27,0 кВ / 2 = 13,5 кВ.

Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см². Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Решение

Энергия заряженного плоского конденсатора равна

W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,

где С₁ — емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения

Q = C₂·U₂,

где C₂ — емкость конденсатора после раздвижения обкладок, следует, что, так как C₂ = ε₀·S/d₂ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7   Дж.

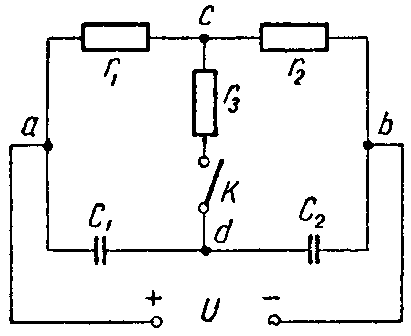
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.

Даны: C₁ = 30 мкФ; C₂ = 20 мкФ; r₁ = 100 Ом. r₂ = 400 Ом. r₃ = 600 Ом, U = 20 В.

Решение

Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям

U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8  В; U 2 =U− U 1 =20−8=12  В.

Рис. 4

Ключ К замкнут. Через сопротивления r₁ и r₂ протекает ток

I= U r 1 + r 2 = 20 500 =0,04  А,

а через сопротивление r₃ ток не протекает.

Поэтому точки c и d равнопотенциальны (φ_c = φ_d). Следовательно, напряжение между точками a и c (U_ac = φ_a — φ_c) равно напряжению между точками a и d (U_ad = φ_a — φ_d).

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

U_C1 = I·r₁ = 0,04·100 = 4 В.

Аналогично напряжение на втором конденсаторе равно

U_C2 = I·r₂ = 0,04·400 = 16 В.

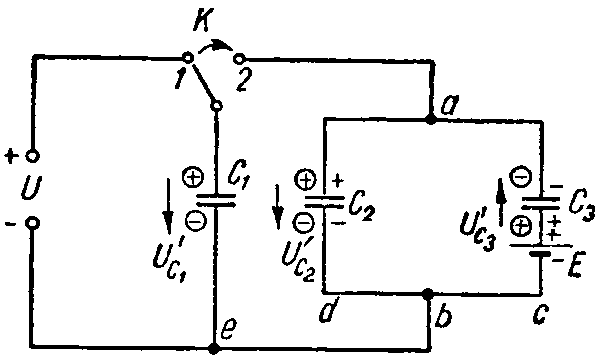
Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ предварительно не был заряжен.

Рис. 5

Решение

Когда рубильник находится в положении 1, то конденсатор C₁ заряжен до напряжения U и его заряд равен

Q = C₁·U = 5·10^–6·25 = 125·10^–6 Кл.

После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C₁ и C₂ (рис. 5). Обозначим эти заряды через Q’₁ и Q’₂.

На основании закона сохранения электричества имеем

Q = Q’₁ + Q’₂ = 125 10^–6 Кл. (1)

По второму закону Кирхгофа имеем

0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,

или

Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0.   (2)

Решая уравнения (1) и (2), найдем

Q’₁ = 5 10^–6 Кл; Q’₂ = 120 10^–6 Кл.

Доставка свежих и аппетитных японских суши в Новороссийске – ям ям..

Напряжение на зажимах конденсаторов станет равным

U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1  В.

Энергия обоих конденсаторов будет равна

W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6   Дж.

Подсчитаем энергию, которая была запасена в конденсаторе С₁, при его подключении к источнику электрической энергии

W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6   Дж.

Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10^–6 — 62,5·10^–6 = 1500·10^–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C₁ в конденсатор C₂ после перевода рубильника в положение 2.

Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.

Рис. 6

Решение

Рубильник находится в положении 1. Заряд конденсатора C₁ равен

Q₁ = C₁·U = 10·10^–6·30 = 0,3·10^–3 Кл.

В указанном положении рубильника конденсаторы C₂ и C₃ соединены последовательно друг с другом, поэтому их заряды равны: Q₂ = Q₃. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем

E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,

откуда

Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3   Кл.

При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’₁, Q’₂ и Q’₃. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.

Для узла a

Q’₁ + Q’₂ — Q’₃ = Q₁ + Q₂ — Q₃. (1)

Для контура 2ebda2

0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .

Для контура bcadb

E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .

Уравнения (1) — (3), после подстановки числовых значений величин, примут вид

Q’₁ + Q’₂ — Q’₃ = 0,3·10^–3; (4)

3Q’₁ — Q’₂ = 0; (5)

2Q’₂ + Q’₃ = 3·10^–3. (6)

Решая совместно уравнения (4) — (6), получим

Q’₁ = 0,33·10^–3 Кл; Q’₂ = 0,99·10^–3 Кл; Q’₃ = 1,02·10^–3 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.

Напряжения на конденсаторах после перевода рубильника будут равны

U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33  В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33  В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17  В.

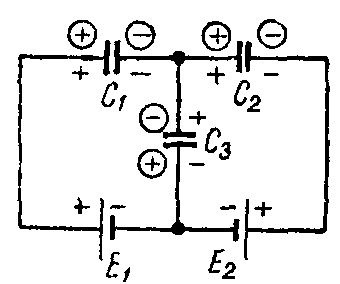
Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C₁ = 5 мкФ; C₂ = 4 мкФ; C₃ = 3 мкФ; э. д. с. источников E₁ = 20 В и E₂ = 5 В.

Рис. 7

Решение

Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках

− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .

Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q₁ = 50 мкКл; Q₂ = 20 мкКл; Q₃ = –30 мкКл.

Таким образом, истинная полярность зарядов на обкладках конденсаторов C₁ и C₂ соответствует выбранной, а у конденсатора C₃ — противоположна выбранной.

Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C₁ = 2 мкФ; C₂ = 3 мкФ; C₃ = 5 мкФ; C₄ = 1 мкФ; C₅ = 2,4 мкФ.

Рис. 8

Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол. Фото на Купчинской 32 – Ксерокс распечатка документов Купчино.

Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.

Решение

1-й способ. Звезду емкостей C₁, C₂ и C₃ (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)

C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6  мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0  мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5  мкФ.

Емкости C₁₂ и C₅ оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость

C₆ = C₁₂ + C₅ = 3 мкФ.

Аналогично

C₇ = C₁₃ + C₄ = 2 мкФ.

Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется

C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7  мкФ.

Вычислим напряжение на каждом из конденсаторов.

На конденсаторе C₇ напряжение равно

U 7 = C 6 C 6 + C 7 ⋅U=6  В.

Таково же напряжение и на конденсаторах C₄ и C₁₃

U₄ = U₃₁ = 6 В.

Напряжение на конденсаторе C₆ равно

U₆ = U — U₇ = 4 В;

U₅ = U₁₂ = 4 В.

Вычислим заряды

Q₄ = C₄·U₄ = 6·10^–6 Кл;

Q₅ = C₅·U₅ = 9,6·10^–6 Кл;

Q₁₂ = C₁₂·U₁₂ = 6·10^–6 Кл;

Q₁₃ = C₁₃·U₃₁ = 2,4·10^–6 Кл.

По закону сохранения электричества для узла 1 схем 8, а и б имеем

–Q₄ — Q₁ + Q₅ = –Q₄ — Q₁₃ + Q₁₂ + Q₅,

отсюда

Q₁ = Q₁₃ — Q₁₂ = 3,6·10^–6 Кл,

а напряжение на конденсаторе, емкостью C₁ составляет

U 1 = Q 1 C 1 =1,8  В.

Далее находим напряжения и заряды на остальных конденсаторах

U₃₁ = U₁ + U₃,

отсюда

U₃ = U₃₁ — U₁ = 4,2 В;

Q₃ = C₃·U₃ = 21·10^–6 Кл,

также

U₁₂ = U₂ — U₁ = 4,2 В,

откуда

U₂ = U₁₂ + U₁ = 5,8 В;

Q₂ = C₂·U₂ = 17,4·10^–6 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.

2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)

для узла 1

Q₅ — Q₁ — Q₄ = 0; (1)

для узла О

Q₁ + Q₂ — Q₃ = 0; (2)

для контура О13О

Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0;  (3)

для контура О12О

Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0;  (4)

для контура a3О2b

Q 3 C 3 + Q 2 C 2 =U.  (5)

Система уравнений (1) — (5) — содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы С_ab можно найти из отношения

C ab = Q U ,

где Q = Q₃ + Q₄, или Q = Q₂ + Q₅.

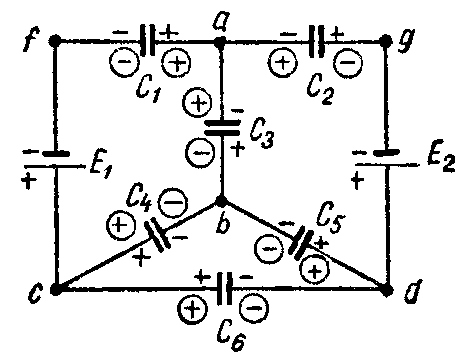
Задача 9. В схеме рис. 9 найти распределение зарядов, если E₁ = 20 В; E₂ = 7 В; C₁ = 7 мкФ; C₂ = 1 мкФ; C₃ = 3 мкФ; C₄ = 4 мкФ; C₅ = C₆ = 5 мкФ.

Рис. 9

Решение

При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:

для узла а

Q₁ + Q₂ + Q₃ = 0;

для узла b

–Q₃ — Q₄ — Q₅ = 0;

для узла c

–Q₁ + Q₄ + Q₆ = 0;

для контура afcba

E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;

ля контура gdbag

E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;

для контура cbdc

0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .

Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды

Q₁ = 35 мкКл; Q₂ = –5 мкКл; Q₃ = –30 мкКл;

Q₄ = 20 мкКл; Q₅ = 10 мкКл; Q₆ = 15 мкКл.

Таким образом, истинные знаки зарядов Q₁, Q₄, Q₅ и Q₆ соответствуют выбранным, а знаки Q₂ и Q₃ противоположны выбранным.

Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.

Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C₁ = 6 мкФ; C₂ = 2 мкФ; C₃ = 3 мкФ; r₁ = 500 Ом; r₂ = 400 Ом; U = 45 В.

Рис. 10

Решение

Через сопротивления протекает ток

I= U r 1 + r 2 =0,05  А.

Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:

− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,

или

Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .

Решив эту систему уравнений, найдем, что

Q₁ = 90 мкКл; Q₂ = 60 мкКл; Q₃ = 30 мкКл.

---

последовательное соединение конденсаторов,
параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами

Комментарии