Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Дифферен. функций нескольких переменных. Найти d^2z/dx^2
|
|||
|
z=arctg((x+y)/(1-xy)) Найти d^2z/dx^2 , d^2z/dxdy, d^z/dy^2
|
||
| Вернуться к началу |
|
||
|
Andy |
Заголовок сообщения: Re: Дифферен. функций нескольких переменных. Найти d^2z/dx^2
|
|
Если выражение не сокращается, то в общем случае это ещё не свидетельствует о наличии проблемы. Правда, в данном случае выражения получаются достаточно простыми. Например, [math]frac{partial^2 z}{partial x^2}=-frac{2x}{left( x^2+1 right)^2}.[/math] Значит, нужно искать ошибку в вычислениях. Проверить себя можно, например, здесь.
|
|
| Вернуться к началу |
|
|
Yurik |
Заголовок сообщения: Re: Дифферен. функций нескольких переменных. Найти d^2z/dx^2
|
|
Вольфрам рекомендует использовать правило цепи.
|
|
| Вернуться к началу |
|
|
searcher |
Заголовок сообщения: Re: Дифферен. функций нескольких переменных. Найти d^2z/dx^2
|
|
djeak11 писал(а): Начинаю делать получается огромные выражения Если совсем невмоготу, то можно попробовать упростить исходное выражение (типа сумма арктангенсов).
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Дифферен. функций нескольких переменных Найти du/dt если
в форуме Дифференциальное исчисление |
djeak11 |
1 |
791 |
29 мар 2016, 21:30 |
|
Дифференциалы функций нескольких переменных
в форуме Дифференциальное исчисление |
makc2299 |
1 |
184 |
13 фев 2019, 19:41 |
|
Дифференцирование функций нескольких переменных
в форуме Дифференциальное исчисление |
mk00 |
3 |
247 |
04 мар 2021, 23:52 |
|
Дифференциальное исчисление функций нескольких переменных
в форуме Дифференциальное исчисление |
katavagner |
1 |
284 |
04 янв 2017, 11:19 |
|
Дифференциальное исчисление функций нескольких переменных
в форуме Дифференциальное исчисление |
tittotop |
1 |
278 |
21 май 2015, 19:33 |
|
Дифференциальное исчисление функций нескольких переменных
в форуме Дифференциальное исчисление |
photographer |
1 |
436 |
30 май 2013, 12:24 |
|
Дифференцирование функций заданых нескольких переменных
в форуме Дифференциальное исчисление |
ladislaus232 |
1 |
226 |
18 апр 2021, 22:34 |
|
Найти предел функции нескольких переменных
в форуме Пределы числовых последовательностей и функций, Исследования функций |
arrapato |
2 |
566 |
18 апр 2015, 13:50 |
|
Найти экстремум функции нескольких переменных (Демидович)
в форуме Дифференциальное исчисление |
boode |
9 |
1043 |
24 май 2017, 14:03 |
|
Функции нескольких переменных
в форуме Дифференциальное исчисление |
never-sleep |
1 |
448 |
12 апр 2014, 17:46 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
[АссолЬ]
Знаток
(321),
закрыт
5 лет назад
объясните чайнику. ничего не понимаю.
или это производная от dz/dy, в которой х – число, а у – переменная????
Трудное детство
Оракул
(70141)
10 лет назад
z – это сложная функция зависящая от двух переменных х и у, она описывает некоторую поверхность. смешанная производная z“(x,y) находится так. сначала берем производную по х, считая у постоянной, потом – по у считая х постоянной. например z=x^2+5xy^2-6y^3, z`(x)=2x+5y^2, z“(x,y)=10y. при этом, если мы сначала возмем производную по у, а потом по х, результат не изменится. на самом деле z`(y)=10xy-18y^2, z“(y,x)=10y.
Решение: согласно задания, нужно найти дифференциал второго порядка (d^2z) функции, заданной неявно, в точке.
Дифференциал второго порядка находится по формуле $$d^2z = frac{partial^2z}{partial x^2}dx^2 + 2frac{partial^2z}{partial x partial y}dxdy + frac{partial^2z}{partial y^2}dy^2 quad (1)$$
1. Найдем частные производные первого порядка функции (z(x,y)) заданной неявно.
Найдем частные производные функции двух переменных (z(x,y)), которая заданна равенством (F(x,y,z) = 0) (неявно заданна), где (F(x,y,z)) – дифференцируемая функция переменных (x,y,z) и (F'(x,y,z) ne 0).
Вычислим частные производные функции по формулам $$ frac{partial z}{partial x} = -frac{F’_x(x,y,z)}{F’_z(x,y,z)}$$где
(F’_x ) – частная производная функции (F(x,y,z)) по (x) – независимая переменная, а (y,z) – константы $$F’_x = (-y^2+yx+6yz+2x^2-3xz-z^2-8)’_x = y+4x-3z$$
(F’_y ) – частная производная функции (F(x,y,z)) по (y) – независимая переменная, а (x,z) – константы $$F’_y = (-y^2+yx+6yz+2x^2-3xz-z^2-8)’_y = -2y+x+6z$$
(F’_z ) – частная производная функции (F(x,y,z)) по (z) – независимая переменная, а (x,y) – константы $$F’_z = (-y^2+yx+6yz+2x^2-3xz-z^2-8)’_z = 6y-3x-2z$$
получили частные производные $$ z’_x = frac{partial z}{partial x} = -frac{y+4x-3z}{6y-3x-2z}$$$$ z’_y = frac{partial z}{partial y} = -frac{-2y+x+6z}{6y-3x-2z}$$
2. Найдем частные производные второго порядка функции (z(x,y)).
$$frac{partial^2z}{partial x^2} = frac{partial}{partial x}(frac{partial z}{partial x}) = (z’_x)’_x = (-frac{y+4x-3z}{6y-3x-2z})’_x = $$$$ =-frac{(4-3z’_x)(6y-3x-2z) – (y+4x-3z)(-3-2z’_x)}{(6y-3x-2z)^2} $$
$$frac{partial^2z}{partial y^2} = frac{partial}{partial y}(frac{partial z}{partial y}) = (z’_y)’_y = (-frac{-2y+x+6z}{6y-3x-2z})’_y = $$$$ = -frac{(-2+6z’_y)(6y-3x-2z) – (-2y+x+6z)(6-2z’_y)}{(6y-3x-2z)^2}$$
$$frac{partial^2z}{partial x partial y} = frac{partial}{partial y}(frac{partial z}{partial x}) = (z’_x)’_y = (-frac{y+4x-3z}{6y-3x-2z})’_y = $$$$ = -frac{(1-3z’_y)(6y-3x-2z) – (y+4x-3z)(6-2z’_y)}{(6y-3x-2z)^2}$$
Подставляем результат в (1)
$$d^2z = -frac{(4-3z’_x)(6y-3x-2z) – (y+4x-3z)(-3-2z’_x)}{(6y-3x-2z)^2}dx^2 – $$$$ 2frac{(1-3z’_y)(6y-3x-2z) – (y+4x-3z)(6-2z’_y)}{(6y-3x-2z)^2}dxdy – $$$$-frac{(-2+6z’_y)(6y-3x-2z) – (-2y+x+6z)(6-2z’_y)}{(6y-3x-2z)^2}dy^2 $$
3. Найдем значений дифференциала второго порядка функции (z(x,y)) с координатами ((x_0=0;y_0=3;z_0=1)).
Найдем значения частных производных первого порядка в точке
$$z’_x(0;3;1) = -frac{y+4x-3z}{6y-3x-2z} = -frac{3+4*0-3*1}{6*3-3*0-2*1} = 0$$
$$z’_y(0;3;1) = -frac{-2y+x+6z}{6y-3x-2z} = -frac{-2*3+0+6*1}{6*3-3*0-2*1} = 0$$
Найдем значения частных производных второго порядка в точке $$frac{partial^2z}{partial x^2} = -frac{(4-3z’_x)(6y-3x-2z) – (y+4x-3z)(-3-2z’_x)}{(6y-3x-2z)^2} = $$$$ =-frac{4(6*3-3*0-2*1) – (3+4*0-3*1)(-3)}{(6*3-3*0-2*1)^2} = -frac{1}{4}$$
$$frac{partial^2z}{partial y^2} = -frac{(-2+6z’_y)(6y-3x-2z) – (-2y+x+6z)(6-2z’_y)}{(6y-3x-2z)^2} =$$$$= -frac{(-2+6*0)(6*3-3*0-2*1) – (-2*3+0+6*1)(-3-2*0)}{(6*3-3*0-2*1)^2} = frac{1}{8}$$
$$frac{partial^2z}{partial x partial y} = -frac{(1-3z’_y)(6y-3x-2z) – (y+4x-3z)(6-2z’_y)}{(6y-3x-2z)^2} = $$$$ =-frac{(1-3*0)(6*3-3*0-2*1) – (3+4*0-3*1)(6-2*0)}{(6*3-3*0-2*1)^2} = -frac{1}{16}$$
Подставляем результат в (1)
$$d^2z = -frac{1}{4}dx^2 – 2frac{1}{16}dxdy + frac{1}{8}dy^2 $$
Ответ: дифференциал второго порядка в точке равен (d^z(0;3) = -frac{1}{4}dx^2 – frac{1}{8}dxdy + frac{1}{8}dy^2)
Мария Гуськова
20 октября 2018 · 2,4 K
Люблю смотреть российские сериалы, играть в шахматы и путешествовать. · 26 дек 2018
- Находим производную по ху
1.1. Находим первую производную по х: z’=(cos xy)’=-ysin(xy)
1.2. Находим вторую производную по y: z”=(-ysin(xy))’= -sin(xy)-yxcos(xy)
- Находим производную по ух
2.1. Находим первую производную по y: z’=(cos xy)’= -хsin(xy)
2.2. Находим вторую производную по х: z”=(-хsin(xy))’= -sin(xy)-xycos(xy)
Таким образом, в обоих случаях производные совпали, значит
d^2z/dxdy=d^2z/dydx, если z=cos xy
1,3 K
Комментировать ответ…Комментировать…

|
дz |
= 2xy; |
дz |
= 2; |
||||
|
дx |
дx P |
||||||
|
дz |
= x2 ; |
дz |
|||||
|
= 1. |
|||||||
|
дy |
|||||||
|
дy P |
Следовательно, grad z=2i+j (рис. 10).
Производные и дифференциалы высших порядков
1°. Частные производные высших порядков. Частными производными второго порядка
функции z=f(х,у) называются частные Производные от ее частных производных первого порядка.
Для производных второго порядка употребляются обозначения
|
д2 z |
= f ”xx ( x, y ); |
||
|
дx2 |
|||
|
д2 z |
= f ”xx ( x, y ). |
||
|
дxдy |
|||
Аналогично определяются и обозначаются частные производные порядка выше второго.
Если частные производные, подлежащие вычислению, непрерывны, то результат многократного дифференцирования не зависит от порядка дифференцирования.
Пример. Найти частные производные второго порядка от функции z = arctg xy .
Решение. Найдем сначала частные производные первого порядка:
|
дz |
= |
1 |
1 |
= |
y |
, |
||||||||||||||||||||||||||||||||||||||||
|
дx |
1 |
+ |
x2 |
y |
x2 |
+ y2 |
||||||||||||||||||||||||||||||||||||||||
|
y2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
дz |
1 |
x |
x |
|||||||||||||||||||||||||||||||||||||||||||
|
= |
− |
= − |
. |
|||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||
|
дy |
x |
y |
x |
+ y |
||||||||||||||||||||||||||||||||||||||||||
|
1 |
+ |
|||||||||||||||||||||||||||||||||||||||||||||
|
y2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
Теперь дифференцируем вторично: |
||||||||||||||||||||||||||||||||||||||||||||||
|
д2 z |
= |
д |
y |
= − |
2xy |
, |
||||||||||||||||||||||||||||||||||||||||
|
дx2 |
дx |
x2 + y2 |
(x2 + y2 )2 |
|||||||||||||||||||||||||||||||||||||||||||
|
д2 z |
д |
x |
2xy |
|||||||||||||||||||||||||||||||||||||||||||
|
= |
− |
= |
. |
|||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
(x |
2 |
2 2 |
|||||||||||||||||||||||||||||||||||||||||
|
дy |
x |
+ y |
+ y |
|||||||||||||||||||||||||||||||||||||||||||
|
дy |
) |
(x2 − y2 ) |
||||||||||||||||||||||||||||||||||||||||||||
|
д2 z |
= |
д |
y |
= |
1(x2 |
+ y2 )− |
2y y |
= |
||||||||||||||||||||||||||||||||||||||
|
. |
||||||||||||||||||||||||||||||||||||||||||||||
|
дxдy |
дy |
x2 + y2 |
(x2 + y2 )2 |
(x2 + y2 )2 |
|
Заметим, что так называемую «смешанную» частную производную можно найти и иначе, а |
||||||||||||||||||||||||||
|
д2 z |
д2 z |
д |
x |
1 |
(x2 + y2 )− 2x x |
(x2 − y2 ) |
||||||||||||||||||||
|
именно: |
= |
= |
− |
= − |
= |
. |
||||||||||||||||||||
|
2 |
(x |
2 |
2 |
2 |
(x |
2 |
2 |
2 |
||||||||||||||||||
|
x |
+ y |
2 |
+ y |
+ y |
||||||||||||||||||||||
|
дxдy дyдx дx |
) |
) |
2°. Дифференциалы высших порядков. Дифференциалом второго порядка функции z=f(х, у)
называется дифференциал от дифференциала (первого порядка) этой функции d²z=d(dz). Аналогично определяются дифференциалы функции г порядка выше второго, например:
d³z=d(d²z) и, вообще, d n z = d (d n−1z).
68

Если z=f(х,у), где х и y — независимые переменные, то дифференциал 2-го порядка функции г вычисляется по формуле
|
d 2 z = |
д2 z dx2 |
+ 2 |
д2 z |
dxdy + |
д2 z dy2 . |
(1) |
|
|
дxдy |
|||||||
|
дx2 |
дy2 |
Вообще, справедлива символическая формула
|
д |
д |
n |
||||
|
d n z = dx |
+ dy |
z , |
||||
|
дx |
||||||
|
дy |
которая формально развертывается по биномиальному закону.
Если z=f(х,у), где аргументы х и у суть функции одного или нескольких независимых переменных, то
|
d |
2 |
z = |
д2 z |
dx |
2 |
+ 2 |
д2 z |
dxdy + |
д2 z |
dy |
2 |
+ |
дz |
d |
2 |
x + |
дz |
d |
2 |
y .(2) |
|
дx2 |
дxдy |
дy2 |
дx |
дy |
||||||||||||||||
Если х и у — независимые переменные, d²x=0, d²y=0 и формула (2) становится тождественной формуле (1).
Пример. Найти полные дифференциалы 1-го и 2-го порядков функции z = 2x2 − 3xy − y2 .
|
Решение. 1-й способ. Имеем: |
дz |
= 4x − 3y, |
дz |
− 3x − 2y . |
|||||||||||||||||
|
дx |
дy |
||||||||||||||||||||
|
Поэтому |
dz = |
дz |
dx + |
дz |
dy = (4x − 3y)dx − (3x + 2y)dy . |
||||||||||||||||
|
дx |
дy |
||||||||||||||||||||
|
Далее, d |
2 |
z = |
д2 z |
dx |
2 |
+ 2 |
д2 z |
дxdy + |
д2 z |
dy |
2 |
= |
4dx |
2 |
− 6дxdy − 2dy |
2 |
. |
||||
|
дx2 |
дxдy |
дy2 |
|||||||||||||||||||
2-й способ. Дифференцированием находим:
dz = 4xdx − 3(ydx + xdy) − 2ydy = (4x − 3y)dx − (3x + 2y)dy .
Дифференцируя ещё раз и помня, что dx и dy не зависят от х и у, получим: d 2 z = (4dx − 3dy)dx − (3dx + 2dy)dy = 4dx2 − 6dxdy − 2dy2 .
Интегрирование полных дифференциалов
1°. Условие полного дифференциала. Для того чтобы выражение Р(х,у)dx+Q(х,у)dу, где функции P(х,y) и Q(х,у) непрерывны в односвязной области D вместе со своими частными производными первого порядка, представляло собой в области D полный дифференциал
некоторой функции u(х,у), необходимо и достаточно выполнение условия ддQx ≡ ддPy .
Пример. Убедится в том, что выражение (2x+y)dx+(x+2y)dy=du= ддux dx = ддuy dy , где u —
искомая функция.
По условию ддux = 2x + y , следовательно, u = ∫(2x + y)dx = x2 + xy + ϕ (y) .
Но, с другой стороны, ддuy = x + ϕ ‘(y) = x + 2y , откуда ϕ ‘(y) = 2y ,ϕ (y) = y2 + C и
u = x2 + xy + y2 + C .
Окончательно, (2x + y)dx + (x + 2y)dx = d (x2 + xy + y2 + C).
69

2º. Случай трех переменных. Аналогично выражение P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz, где
P(x,y,z)dx, Q(x,y,z)dy, R(x,y,z)dz — непрерывные, вместе со своими частными производными 1-го порядка, функции переменных х, у и z, тогда и только тогда представляет собой полный дифференциал некоторой функции u(х,у,z), когда выполнены условия
ддQx ≡ ддPy , ддRy ≡ ддQz , ддPz ≡ ддRx .
Пример. Убедится в том, что выражение (3x2 + 3y −1)dx + (z2 + 3x)dy + (2yz + 1)dz есть полный дифференциал некоторой функции, и найти эту функцию.
Решение. Здесь P=3x²+3y-1, Q=z²+3x, R=2yz+1. Устанавливаем, что
ддQx = ддPy = 3, ддRy = ддQz = 2z, ддPz = ддRx = 0
и, следовательно, (3x2 + 3y −1)dx + (z2 + 3x)dy + (2yz + 1)dz = du = ддux dx + ддuy dy + ддuz dz , где u
— искомая функция.
Имеем: ддux = 3x2 + 3y −1, значит u = ∫(3x2 + 3y −1)dx = x2 + 3xy − x + ϕ (y, z) .
С другой стороны,
ддuy = 3x + ддϕy = z2 + 3x, ддuz = ддϕz = 2yz + 1,
откуда ддϕy = z2 и ддϕz = 2yz + 1. Задача сводится к отысканию функции двух переменных
ϕ (у,z), частные производные которой известны и выполнено условие полного дифференциала. Находим ϕ :
ϕ (y, z) = ∫z2dy = yz2 +ψ (z)
ддϕz = 2yz +ψ ‘(z) = 2yz + 1, ψ ‘(z) = 1,ψ (z) = z + C,
т. е. ϕ (y, z) = yz2 + z + C . Окончательно, u=x²+3xy-x+yz²+z+C.
Дифференцирование неявных функций
1°. Случай одной независимой переменной. Если уравнение f(х,у) =0, где f(х,у) — дифференцируемая функция переменных х и у, определяет у как функцию от х, то производная этой неявно заданной функции при условии, что f‘y(х, у)≠0, может быть найдена по формуле
|
dy |
= − |
fx ‘(x, y) |
. |
(1) |
|||||
|
dx |
f y ‘(x, y) |
||||||||
|
Производные высших порядков находятся последовательным дифференцированием |
|||||||||
|
формулы (1). |
|||||||||
|
Пример. Найти |
dy |
и |
d 2 y |
, если (x²+y²)³-3(x²+y²)+1=0. |
|||||
|
dx |
dx2 |
||||||||
|
70 |
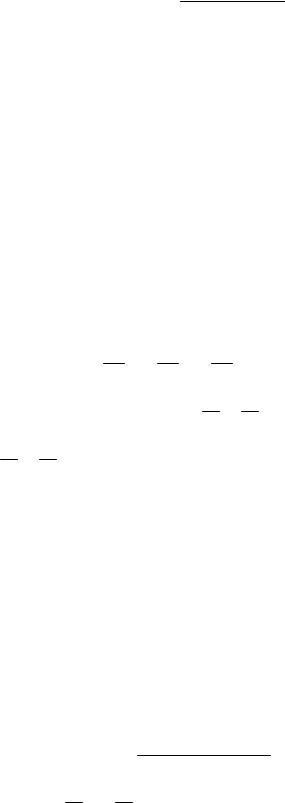
Решение. Обозначая левую часть данного уравнения через f(х,y) найдем частные производные
f’x(x,y)=3(x²+y²)²·2x-3·2x=6x[(x²+y²)-1], f’y(x,y)=3(x²+y²)²·2y-3·2y=6y[(x²+y²)-1].
Отсюда, применяя формулу (1), получим:
|
dy |
fx ‘(x, y) |
6x[(x2 + y2 )2 −1] |
x |
|||
|
= − |
= − |
6y[(x2 + y2 )2 −1]= − |
. |
|||
|
dx |
f y ‘(x, y) |
y |
Чтобы найти вторую производную, продифференцируем по х найденную первую производную, учитывай при этом, что у есть функция х:
|
dy |
x |
|||||||||||||||
|
d 2 y |
d |
x |
y − x |
− |
y2 + x2 |
|||||||||||
|
1 y − x dx |
y |
|||||||||||||||
|
= |
− |
= − |
= − |
= − |
. |
|||||||||||
|
dx2 |
y2 |
y2 |
y2 |
|||||||||||||
|
dx |
y |
2°. Случай нескольких независимых переменных. Аналогично, если уравнение F(х, у, z)=0, где F(х, у, z) — дифференцируемая функция переменных х, у и z, определяет z как функцию независимых переменных х и у и Fz(x, у, z)≠0, то частные производные этой неявно заданной функции, вообще говоря, могут быть найдены по формулам
|
дz |
F ‘(x,y,z) |
дz |
Fy‘(x,y,z) |
|||||
|
= − |
x |
, |
= − |
(2) |
||||
|
дx |
Fz‘(x,y,z) |
дy |
||||||
|
Fz‘(x,y,z) . |
Другой способ нахождения производных функции z следующий: дифференцируя уравнение
F(х, у, z) = 0, получим:
ддFx dx + ддFy dy + ддFz dz = 0.
Отсюда можно определить dz, а следовательно, ддxz и ддyz .
Пример. Найти ддxz и ддyz , если x² – 2y²+3z² – yz+y=0.
Решение.
1-й способ. Обозначая левую часть данного уравнения через F(х, у, z), найдем частные производные F’x(x,y,z)=2x, F’y(x,y,z)=-4y-z+1, F’z(x,y,z)=6z-y.
Применив формулы (2), получим:
|
дz |
= − |
Fx‘ ( x, y,z ) |
= − |
2x |
; |
||||||
|
дx |
F ‘ ( x, y,z ) |
6 z − y |
|||||||||
|
z |
|||||||||||
|
дz |
− |
Fy‘ ( x, y,z ) |
= − |
1 − 4 y − z |
. |
||||||
|
дy |
F ‘ ( x, y,z ) |
6 z − y |
|||||||||
|
z |
2-й способ. Дифференцируя данное уравнение, получим:
2х dx-4y dy+6z dz-y dz-z dy+dy=0
Отсюда определяем dz, т. е. полный дифференциал неявной функции:
dz = 2xdx + (1− 4y − z)dy . y − 6z
Сравнивая с формулой dz = ддxz dx + ддyz dy , видим, что
71

|
дz |
= |
2x |
, |
дz |
= |
1− 4y − z |
. |
|
y − 6z |
дy |
||||||
|
дx |
y − 6z |
3°. Система неявных функций. Если система двух уравнений
F(x, y,u.v)= 0,G(x, y,u.v)= 0,
определяет u и v как функции переменных х и у и якобиан
|
D( F ,G ) |
дF |
дF |
|||||
|
= |
дu |
дv |
≠ 0 , |
||||
|
D( u,v ) |
|||||||
|
дG |
дG |
||||||
|
дu |
дv |
то дифференциалы этих функций (а следовательно, и их частные производные) могут быть найдены из системы уравнений
|
dx + |
∂F |
dy + |
∂F |
du + |
∂F |
dv = 0, |
|
|
∂y |
∂u |
∂v |
(3) |
||||
|
dx + |
∂G |
dy + |
∂G |
du + |
∂G |
||
|
dv = 0. |
|||||||
|
∂y |
∂u |
∂v |
Пример: Уравнения u+v=x+y, xu+yv=1 определяют u и v как функции х и у; найти
ддux , ддuy , ддvx , ддvy .
Решение. 1-й способ. Дифференцируя оба уравнения по х, получим:
|
дu |
+ |
дv |
= 1, |
||||||||||||||
|
дx |
дx |
||||||||||||||||
|
u + x |
дu |
+ y |
дv |
= 0, |
|||||||||||||
|
дx |
|||||||||||||||||
|
дx |
|||||||||||||||||
|
отсюда |
|||||||||||||||||
|
дu |
= − |
u + y |
, |
дv |
= |
u + x |
. |
||||||||||
|
дx |
x − y |
дx |
|||||||||||||||
|
x − y |
Аналогичным образом найдем:
|
дu |
= − |
u + y |
, |
дv |
= |
u + x |
. |
|
дy |
x − y |
дy |
|||||
|
x − y |
2-й способ. Дифференцированием находим два уравнения, связывающие дифференциалы всех четырех переменных: du+dv=dx+dy, x du+u dx+y dv+v dy=0.
Решив эту систему относительно дифференциалов du и dv, получим:
|
du = − |
( u + y )dx + ( v + y )dy |
, |
dv = |
( u + x )dx + ( v + x )dy |
. |
||||||||||||||
|
x − y |
x − y |
||||||||||||||||||
|
Отсюда |
|||||||||||||||||||
|
дu |
= − |
u + y |
, |
дu |
= − |
u + x |
, |
||||||||||||
|
дx |
x − y |
дy |
x − y |
||||||||||||||||
|
дu |
= |
u + y |
, |
дu |
= |
u + x |
. |
||||||||||||
|
дx |
|||||||||||||||||||
|
x − y |
дy |
x − y |
4°. Параметрическое задание функции. Если функция г переменных х и у задана параметрически уравнениями x=x(u,v), y=y(u,v), z=z(u,v) и
72

|
D(x, y) |
дx |
дx |
|||||
|
= |
дu |
дv |
≠ 0 |
, |
|||
|
D(u,v) |
дy |
дy |
|||||
|
дu |
дv |
то дифференциал этой функции может быть найден из системы уравнений
|
∂x |
du + |
∂x |
dv, |
|||
|
dx = |
||||||
|
∂u |
∂v |
|||||
|
∂y |
∂y |
|||||
|
du + |
dv, |
|||||
|
dy = |
(4) |
|||||
|
∂u |
∂v |
|||||
|
dz = |
∂z |
du + ∂z dv. |
||||
|
∂u |
∂v |
|||||
Зная дифференциал dz=p dx+q dy, находим частные производные ддxz = p и ддyz = q .
Пример. Функция z аргументов х и у задана уравнениями x=u+v, y=u²+v², z=u²+v² (u≠v).
Найти ддxz и ддyz .
Решение. 1-й способ. Дифференцированием находим три уравнения, связывающие дифференциалы всех пяти переменных:
dx = du + dv,dy = 2udu + 2vdv,
dz = 3u2du + 3v2dv.
Из первых двух уравнений определим du и dv:
|
du = |
2vdx + dy |
, |
dv = |
dy + 2udx |
. |
|
2( v − u ) |
|||||
|
2( v − u ) |
Подставим в третье уравнение найденные значения du и dv:
|
dz = 3u2 2vdx − dy |
+ 3v2 dy − 2udx = 6uv(u − v)dx + 3(v2 − u2 )dy |
= −3uvdx + |
3 (u + v)dy . |
|||||||||||||||||||||||||||||||
|
2(v − u) |
2(v − u) |
2(v − u) |
2 |
|||||||||||||||||||||||||||||||
|
Отсюда |
||||||||||||||||||||||||||||||||||
|
дz |
= −3uv, |
дz |
= |
3 |
(u + v) . |
|||||||||||||||||||||||||||||
|
дx |
дy |
2 |
||||||||||||||||||||||||||||||||
|
2-й способ. Из третьего данного уравнения можно найти: |
||||||||||||||||||||||||||||||||||
|
дz |
= |
3u |
2 |
дu |
+ 3v |
2 |
дv |
; |
дz |
= |
3u |
2 |
дu |
+ 3v |
2 |
дv |
(5) |
|||||||||||||||||
|
дx |
дx |
дx |
дy |
дy |
дy |
|||||||||||||||||||||||||||||
|
Продифференцируем первые два уравнения сначала по х, затем по у: |
||||||||||||||||||||||||||||||||||
|
1 = |
∂u |
+ |
∂v |
, 0 = |
∂u |
+ |
∂v |
, |
||||||||||||||||||||||||||
|
∂x |
∂y |
∂y |
∂y |
|||||||||||||||||||||||||||||||
|
∂u |
∂v |
∂u |
∂v . |
|||||||||||||||||||||||||||||||
|
0 = 2u |
+ 2v |
, 1 = 2u |
+ 2v |
|||||||||||||||||||||||||||||||
|
∂x |
∂x |
∂y |
∂y |
|||||||||||||||||||||||||||||||
Из первой системы найдем:
Из второй системы найдем:
Подставляя выражения ддxz
|
дu |
= |
v |
дv |
= |
u |
. |
||||||||
|
дx |
v − u, дx |
u − v |
||||||||||||
|
дu |
= |
1 |
, |
дv |
= |
1 |
. |
|||||||
|
дy |
2( u − v ) |
дy |
2( u − v ) |
|||||||||||
и ддyz в формулу (5), получим:
73
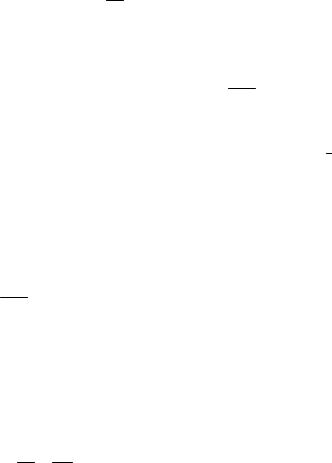
|
дz |
= 3u2 |
v |
+ 3v |
2 |
u |
= −3uv, |
|||||||
|
дx |
v − u |
u − v |
|||||||||||
|
дz |
= 3u2 |
1 |
+ |
3v2 |
1 |
= |
3 |
( u + v ). |
|||||
|
дy |
2(v − u) |
2(u − v) |
2 |
Замена переменных
При замене переменных в дифференциальных выражениях входящие в них производные следует выразить через другие производные по правилам дифференцирования сложной функции.
1°. Замена переменных в выражениях, содержащих обыкновенные производные.
|
Пример. Преобразовать уравнение |
|||||||||
|
x2 |
d 2 y |
+ 2x |
dy |
+ |
a2 |
y = 0 , |
|||
|
dx2 |
dx |
x2 |
|||||||
|
полагая |
x = |
1 |
. |
||||||
|
t |
Решение. Выразим производные от у по х через производные от у по t. Имеем:
|
dy |
dy |
dy |
|||||||||
|
= |
dt |
= |
dt |
||||||||
|
dx |
dx |
1 |
|||||||||
|
dt |
− |
||||||||||
|
t2 |
|||||||||||
|
d dy |
|||||||||||
|
dy |
|||||||||||
|
dt dt |
|||||||||||
|
= − |
2t |
||||||||||
|
dx |
dt |
dt
= −t2 dydt ,
|
d |
2 |
y |
|||
|
+ t2 |
(− t2 )= 2t2 |
||||
|
dt2 |
|||||
+ t2 d 2 2y . dt
Подставляя найденные выражения производных в данное уравнение и заменяя х через 1t ,
получим:
|
1 |
2 |
dy |
2 d 2 y |
1 |
2 |
dy |
2 |
2 |
||||||||||||||||
|
t |
2t |
+ t |
+ 2 |
− t |
+ a |
t |
y = 0 |
|||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||
|
t |
dt |
dt |
t |
|||||||||||||||||||||
|
dt |
или
d 2 2y + a2 y = 0 . dt
|
Пример. Преобразовать уравнение |
||||||||
|
d 2 y |
dy 2 |
dy |
||||||
|
x |
+ |
− |
= 0, |
|||||
|
dx2 |
dx |
dx |
приняв за аргумент у, а за функцию х.
Решение. Выразим производные от у по х через производные от х по у.
dydx = dx1 ; dy
74

d 2 x dy2
d 2 y dx2
|
d 2 x |
||||||
|
d |
1 dy |
= − |
dy2 |
|||
|
dy |
dx |
dx |
dx 2 |
|||
|
dy |
dy |
1 dx dy
= − dx 2 .dy
Подставив эти выражения производных в данное уравнение, будем иметь:
|
d 2 x |
|||||||||||||||||||||||||||||||||
|
dy2 |
1 |
1 |
|||||||||||||||||||||||||||||||
|
x − |
+ |
− |
= 0 , |
||||||||||||||||||||||||||||||
|
dx |
2 |
dx |
2 |
dx |
|||||||||||||||||||||||||||||
|
dy |
|||||||||||||||||||||||||||||||||
|
dy |
dy |
||||||||||||||||||||||||||||||||
|
или, окончательно, |
|||||||||||||||||||||||||||||||||
|
d 2 x |
dx |
2 |
|||||||||||||||||||||||||||||||
|
x |
−1+ |
= 0 . |
|||||||||||||||||||||||||||||||
|
dy2 |
|||||||||||||||||||||||||||||||||
|
dy |
|||||||||||||||||||||||||||||||||
|
Пример. Преобразовать уравнение |
|||||||||||||||||||||||||||||||||
|
dy |
= |
x + y |
, |
||||||||||||||||||||||||||||||
|
dx |
x − y |
||||||||||||||||||||||||||||||||
|
перейдя к полярным координатам |
|||||||||||||||||||||||||||||||||
|
x=r cosφ, y=r cosφ. |
(1) |
||||||||||||||||||||||||||||||||
|
Решение. Рассматривая r как функцию φ, из формул (1) получим: |
|||||||||||||||||||||||||||||||||
|
dх = соsφ dr – r sinφ dφ, dy=sinφ+r cosφ dφ, |
|||||||||||||||||||||||||||||||||
|
отсюда |
|||||||||||||||||||||||||||||||||
|
sinϕ |
dr |
+ r cosϕ |
|||||||||||||||||||||||||||||||
|
dy |
= |
sinϕdr + rcosϕdϕ |
= |
dϕ |
|||||||||||||||||||||||||||||
|
. |
|||||||||||||||||||||||||||||||||
|
dx |
cosϕdr − r sinϕdϕ |
cosϕ |
dr |
− r sinϕ |
|||||||||||||||||||||||||||||
|
dϕ |
|||||||||||||||||||||||||||||||||
|
Подставляя в данное уравнение выражения для х, у и |
dy |
, будем иметь: |
|||||||||||||||||||||||||||||||
|
dx |
|||||||||||||||||||||||||||||||||
|
sinϕ |
dr |
+ r cosϕ |
|||||||||||||||||||||||||||||||
|
dϕ |
= |
sinϕdr + rcosϕdϕ |
, |
||||||||||||||||||||||||||||||
|
dr |
|||||||||||||||||||||||||||||||||
|
cosϕ |
− r sinϕ |
cosϕdr − r sinϕdϕ |
|||||||||||||||||||||||||||||||
|
dϕ |
|||||||||||||||||||||||||||||||||
или, после упрощений, ddrϕ = r .
2°. Замена переменных в выражениях, содержащих частные производные. Пример. Уравнение колебаний струны
|
д2u |
= a2 |
д2u |
(a ≠ 0) |
|
|
дt2 |
дx2 |
|||
преобразовать к новым независимым переменным α иβ , где α = x − αt , β = x + αt .
Решение. Выразим частные производные от u по х и y через частные производные от u по α иβ . Применяя формулы дифференцирования сложной функции
ддut = ддαu ддαt + ддβu ддβt , ддux = ддαu ддαx + ддβu ддβx ,
получим:
75

|
дu |
дu |
дu |
|||||||||
|
= |
(−α ) + |
α |
= α |
||||||||
|
дα |
дβ |
дβ |
|||||||||
|
= |
дu |
1+ |
дu |
1 = |
дu |
+ |
дu |
. |
|||
|
дα |
дβ |
дα |
|||||||||
|
дβ |
Дифференцируем вторично, применяя те же формулы:
|
д2u |
д |
дu |
д |
дu |
дα |
д |
дu |
дβ |
|||||||||||||||||||
|
= |
= |
+ |
= |
||||||||||||||||||||||||
|
дt2 |
дt |
дt |
дβ |
дt |
|||||||||||||||||||||||
|
дt |
дα |
дt |
дt |
||||||||||||||||||||||||
|
д2u |
д2u |
д2u |
д2u |
||||||||||||||||||||||||
|
= α |
− |
( −α ) + |
α |
− |
α = |
||||||||||||||||||||||
|
дα |
2 |
2 |
|||||||||||||||||||||||||
|
дαдβ |
дβ |
дαдβ |
|
д2u |
д2u |
д2u |
|||||||||||||||||||||||||||||||||||
|
= α 2 |
− 2 |
+ |
; |
||||||||||||||||||||||||||||||||||
|
2 |
2 |
||||||||||||||||||||||||||||||||||||
|
дαдβ |
дβ |
||||||||||||||||||||||||||||||||||||
|
дα |
|||||||||||||||||||||||||||||||||||||
|
д2u |
д |
дu |
д |
дu дα |
д |
дu |
дβ |
||||||||||||||||||||||||||||||
|
= |
= |
+ |
= |
||||||||||||||||||||||||||||||||||
|
дx2 |
дx |
дx |
дβ |
дx |
дx |
||||||||||||||||||||||||||||||||
|
дx |
дα |
дx |
|||||||||||||||||||||||||||||||||||
|
д2u |
д2u |
д2u |
д2u |
||||||||||||||||||||||||||||||||||
|
= |
+ |
1 + |
+ |
1 |
= |
||||||||||||||||||||||||||||||||
|
2 |
дαдβ |
дβ |
2 |
||||||||||||||||||||||||||||||||||
|
дα |
дαдβ |
||||||||||||||||||||||||||||||||||||
|
= |
д2u |
+ 2 |
д2u |
+ |
д2u |
. |
|||||||||||||||||||||||||||||||
|
дα 2 |
дαдβ |
дβ 2 |
|||||||||||||||||||||||||||||||||||
Подставив в данное уравнение, будем иметь:
|
2 |
д2u |
д2u |
д2u |
2 |
д2u |
д2u |
д2u |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
α |
− 2 |
+ |
= α |
+ 2 |
+ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дα |
дαдβ |
дβ |
дα |
дαдβ |
дβ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
или |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
д2u |
= 0. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дαдβ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример. Преобразовать уравнение |
x2 |
дz |
+ y2 |
дz |
= z2 , приняв за новые независимые |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дx |
дy |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
переменные u=х, v = |
1 |
− |
1 |
и за новую функцию |
w = |
1 |
− |
1 |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
y |
z |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Решение. Выразим частные производные |
дz |
и |
дz |
через частные производные |
дw |
и |
дw |
. Для |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дx |
дy |
дv |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дu |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
этого продифференцируем данные соотношения между старыми и новыми переменными |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
du = dx, dv = |
dx |
− |
dy |
, |
dw = |
dx |
− |
dz |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
x2 |
y2 |
x2 |
z2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
С другой стороны, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дw = |
дw |
du + |
дw |
dv . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дu |
дv |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поэтому |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дw |
du + |
дw |
dv = |
dx |
− |
dz |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дu |
дv |
z2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
или |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дw |
dx + |
дw dx |
− |
dy |
dx |
− |
dz |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
дu |
дv |
y2 |
= |
x2 |
z2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
2 |
Отсюда
76




