Даны два вектора как найти проекцию - Сайт, где вы сможете решить свои вопросы

Как найти проекцию вектора на вектор?

Для того, чтобы найти проекцию вектора на вектор ($overline{a}$ на $overline{b}$) нужно разделить скалярное произведение этих векторов на длину последнего вектора $overline{b}$ по формуле: $$text{Пр}_{overline{b}} overline{a} = frac{(overline{a},overline{b})}{|overline{b}|}$$

Пример 1

Найти проекцию вектора $overline{a} = (1,2)$ на вектор $overline{b} = (-1,2)$

Решение

Вычисляем скалярное произведение векторов. Умножаем соответствующие координаты и складываем $$(overline{a},overline{b}) = 1 cdot (-1) + 2 cdot 2 = -1 + 4 = 3$$

Находим модуль вектора, на который ищем проекцию $$|overline{b}| = sqrt{(-1)^2 + 2^2} = sqrt{5}$$

Подставляя в формулу проекции вектора $overline{a}$ на направляющий вектор $overline{b}$ получаем искомое значение $$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$text{Пр}_{overline{b}} overline{a} = frac{3}{sqrt{5}}$$

Пример 2

Вычислить проекцию вектора на вектор, если $overline{a} = (1,2,-3)$ и $overline{b} = (2,1,1)$

Решение

Берем скалярное произведение двух векторов. Перемножаем попарно соответствующие координаты и суммируем полученные значения $$(overline{a},overline{b}) = 1 cdot 2 + 2 cdot 1 + (-3) cdot 1 = 2 + 2 – 3 = 1$$

Так как ищем проекцию на вектор $overline{b}$, то вычисляем его модуль (длину) $$|overline{b}| = sqrt{2^2 + 1^2 + 1^2} = sqrt{6}$$

По главной формуле получаем ответ к задаче $$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$

Ответ

$$text{Пр}_{overline{b}} overline{a} = frac{1}{sqrt{6}}$$

Источник

Проекция вектора на ось. Проекция вектора на вектор

Навигация по странице:

Определение проекции вектора на ось
Определение проекции вектора на вектор
Формула вычисления проекции вектора на вектор
Примеры задач на проекцию вектора
- плоские задачи
- пространственные задачи

Определение. Проекцией вектора AB на ось l называется число, равное величине отрезка A₁B₁ оси l, где точки A₁ и B₁ являются проекциями точек A и B на ось l. (рис. 1).

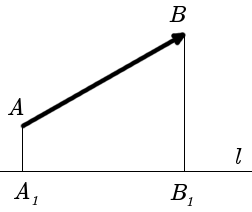рис. 1

Определение. Проекцией вектора a на направление вектора b , называется число, равное величине проэкции вектора a на ось проходящую через вектор b.

Формула вычисления проекции вектора на вектор

Для вычисления проекции вектора a на направление вектора b из определения скалярного произведения получена формула:

Примеры задач на проекцию вектора

Примеры вычисления проекции вектора для плоских задач

Пример 1. Найти проекцию вектора a = {1; 2} на вектор b = {3; 4}.

Решение:

Найдем скалярное произведение этих векторов

a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11

Найдем модуль вектора b

|b| = √3² + 4² = √9 + 16 = √25 = 5

Найдем проекцию вектора a на вектор b

Пр _ba =	a · b	=	11	= 2.2
\|b\|	5

Ответ: Пр _ba = 2.2.

Примеры вычисления проекции вектора для пространственных задачи

Пример 2. Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.

Решение:

Найдем скалярное произведение этих векторов

a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12

Найдем модуль вектора b

|b| = √4² + 2² + 4² = √16 + 4 + 16 = √36 = 6

Найдем проекцию вектора a на вектор b

Пр _ba =	a · b	=	12	= 2
\|b\|	6

Ответ: Пр _ba = 2.

Источник

Содержание:

Формула
Примеры нахождения проекции вектора на вектор

Формула

Чтобы найти проекцию вектора $bar{a}$ на вектор
$bar{b}$, надо
скалярное произведение указанных векторов поделить на
длину (модуль) вектора
$bar{b}$, то есть

$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}$$

В случае если векторы заданы на плоскости и имеют координаты
$bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, то проекция вектора
$bar{a}$ на вектор
$bar{b}$ вычисляется по формуле:

$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{b_{x}^{2}+b_{y}^{2}}}$$

Если векторы заданы в пространстве, то есть имеют координаты bar{a}=left(a_{x} ; a_{y} ; a_{z}right) text { и } bar{b}=left(b_{x} ; b_{y} ; b_{z}right), то проекция вектора
$bar{a}$ на вектор
$bar{b}$ вычисляется по формуле:

$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$

Примеры нахождения проекции вектора на вектор

Пример

Задание. Найти проекцию вектора
$bar{a}$ на вектор
$bar{b}$, если
$bar{a}=(-1 ; 0)$ и $bar{b}=(3 ;-4)$

Решение. Для нахождения проекции вектора
$bar{a}$ на вектор
$bar{b}$, будем использовать формулу

$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{b_{x}^{2}+b_{y}^{2}}}$$

Подставляя в неё координаты заданных векторов, получим:

$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{-1 cdot 3+0 cdot(-4)}{sqrt{3^{2}+(-4)^{2}}}=frac{-3+0}{sqrt{9+16}}=frac{-3}{sqrt{25}}=-frac{3}{5}$$

Ответ. $Пр_{bar{b}} bar{a}=-frac{3}{5}$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти проекцию вектора
$bar{a}=(-2 ; 3 ; 0)$ на вектор
$bar{b}=(-2 ; -1 ; 5)$

Решение. Подставляя координаты заданных векторов в формулу

$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$

получим:

$$Пр_{bar{b}} bar{a}=frac{(bar{a}, bar{b})}{|b|} =frac{-2 cdot(-2)+3 cdot(-1)+0 cdot 5}{sqrt{(-2)^{2}+(-1)^{2}+5^{2}}}=$$
$$=frac{4-3+0}{sqrt{4+1+25}}=frac{1}{sqrt{30}}$$

Ответ. $Пр_{bar{b}} bar{a}=frac{1}{sqrt{30}}$

Читать дальше: как найти длину вектора.

Источник

Проекция вектора на вектор: онлайн-калькулятор

Осуществлять векторное проецирование стало проще с нашим сервисом. Студентам и школьникам, чтобы найти проекцию вектора на вектор при подготовке к занятиям, понадобится только ввести заданные координаты или точки. Дальнейшая последовательность действий определяется автоматически.

Вычисление проекции вектора а на вектор б происходит по формуле:

Пpb→a→=a→·b→b→

После отправки введенных данных на расчет вам доступно подробное решение и точный ответ.

Проекция вектора на вектор онлайн

Чтобы найти проекцию вектора на вектор онлайн по координатам, программа использует следующий алгоритм:

Вычисляем скалярное произведение векторов.
Рассчитываем модуль вектора.
Подставляем данные в формулу и находим проекцию.

Для нахождения проекции по точкам необходимо предварительно вычислить векторы a и b.

На нашем сайте вы сможете не только найти проекцию вектора на вектор онлайн-калькулятором, но и произвести другие действия с векторами. Также в нашем сервисе представлены калькуляторы для решения задач на другие темы по алгебре и геометрии.

Использование сервиса не требует вносить оплату, регистрироваться, оставлять личные данные. Вы можете тренироваться без ограничений по количеству проверок. Каждый раз после отправки примера на расчет вы будете видеть подробное решение. Это позволит разобраться в теме, запомнить последовательность действий и применять их в дальнейшем для решения аналогичных задач.

Если в освоении темы даже после изучения примеров все равно возникают трудности, напишите онлайн-консультанту. Мы подберем грамотного преподавателя по вашему запросу. За минимальное количество занятий по выгодной цене вы заполните пробелы в знаниях.

Источник

В данной публикации мы рассмотрим, что такое проекция вектора на ось или на другой вектор, и приведем формулу, с помощью которой можно найти значение этой проекции. Также разберем примеры решения задач по этой теме.