Даны координаты вершин треугольника как найти высоту

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Пример.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

Решение:

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

   

Таким образом, уравнение прямой BC —

   

Угловой коэффициент прямой, перпендикулярной BC,

   

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

   

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

   

Итак, уравнение высоты, проведённой к стороне BC:

   

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

   

Уравнение прямой AB:

   

Угловой коэффициент перпендикулярной ей прямой

   

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

   

Угловой коэффициент прямой, перпендикулярной AC,

   

Таким образом, уравнение перпендикулярной AC прямой имеет вид

   

Подставив в него координаты точки B(5;-3), найдём b:

   

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

   

Как найти высоту треугольника, если даны координаты точек

Высотой в треугольнике называют отрезок прямой линии, соединяющий вершину фигуры с противолежащей стороной. Этот отрезок обязательно должен быть перпендикулярен стороне, поэтому из каждой вершины можно провести лишь одну высоту. Поскольку вершин в этой фигуре три, высот в нем столько же. Если треугольник задан координатами своих вершин, вычисление длины каждой из высот можно произвести, например, воспользовавшись формулой нахождения площади и рассчитав длины сторон.

Инструкция

Исходите в расчетах из того, что площадь треугольника равна половине произведения длины любой из его сторон на длину высоты, опущенной на эту сторону. Из этого определения вытекает, что для нахождения высоты нужно знать площадь фигуры и длину стороны.

Начните с вычисления длин сторон треугольника. Обозначьте координаты вершин фигуры так: A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃). Тогда длину стороны AB вы сможете рассчитать по формуле AB = √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²). Для двух других сторон эти формулы будут выглядеть так: BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) и AC = √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²). Например, для треугольника с координатами A(3,5,7), B(16,14,19) и C(1,2,13) длина стороны AB составит √((3-16)² + (5-14)² + (7-19)²) = √(-13² + (-9²) + (-12²)) = √(169 + 81 + 144) = √394 ≈ 19,85. Длины сторон BC и AC, рассчитанные таким же способом, будут равны √(15² + 12² + 6²) = √405 ≈ 20,12 и √(2² + 3² + (-6²)) = √49 = 7.

Знания длин трех сторон, полученных на предыдущем шагу, достаточно для вычисления площади треугольника (S) по формуле Герона: S = ¼ * √((AB+BC+CA) * (BC+CA-AB) * (AB+CA-BC) * (AB+BC-CA)). Например, после подстановки в эту формулу значений, полученных из координат треугольника-образца из предыдущего шага, эта формула даст такое значение: S = ¼*√((19,85+20,12+7) * (20,12+7-19,85) * (19,85+7-20,12) * (19,85+20,12-7)) = ¼*√(46,97 * 7,27 * 6,73 * 32,97) ≈ ¼*√75768,55 ≈ ¼*275,26 = 68,815.

Исходя из площади треугольника, рассчитанной на предыдущем шаге, и длин сторон, полученных на втором шаге, вычислите высоты для каждой из сторон. Так как площадь равна половине произведения высоты на длину стороны, к которой она проведена, для нахождения высоты делите удвоенную площадь на длину нужной стороны: H = 2*S/a. Для использованного выше примера высота, опущенная на сторону AB составит 2*68,815/16,09 ≈ 8,55, высота к стороне ВС будет иметь длину 2*68,815/20,12 ≈ 6,84, а для стороны АС эта величина будет равна 2*68,815/7 ≈ 19,66.

Источники:

• даны точки найти площадь треугольника

8

Даны вершины
треугольника.
Найти:

1. длину стороны ВС;

2. уравнение высоты ВС;

3. уравнение высоты, проведённой из вершины
   А;

4. длину высоты, проведённой из вершины
   А;

5. угол В.

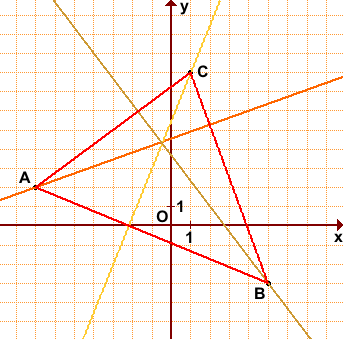
Сделать чертёж.

Дано: А(-8;3), В(4;-2), С(7;2).

РЕШЕНИЕ

1. Длину стороны ВС находим по формуле
   .
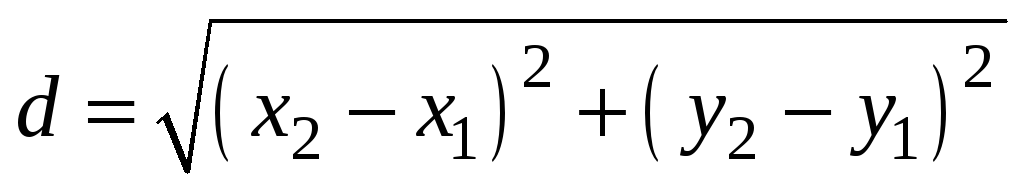   По условию имеем В(4;-2), С(7;2).

1. Найдём уравнение стороны ВС. Найдём
   уравнение прямой, на которой лежит
   сторона ВС. Используем уравнение прямой,
   проходящей через две точки
   ,
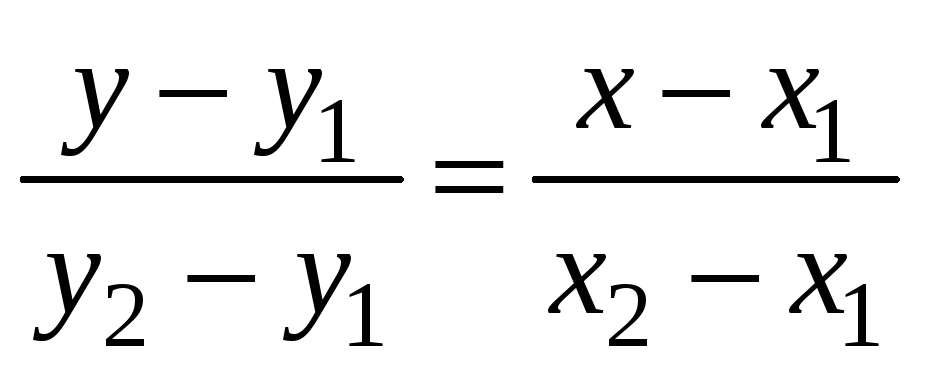   полагая
   

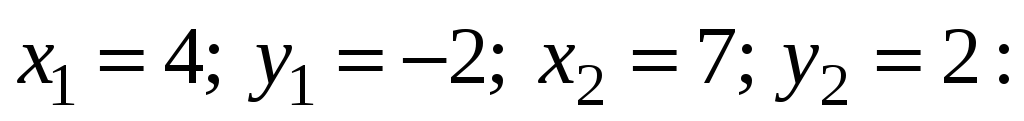
1. Найдём уравнение высоты, проведённой
   из вершины А. При составлении уравнения
   прямой, на которой лежит высота
   треугольника, воспользуемся формулой
   
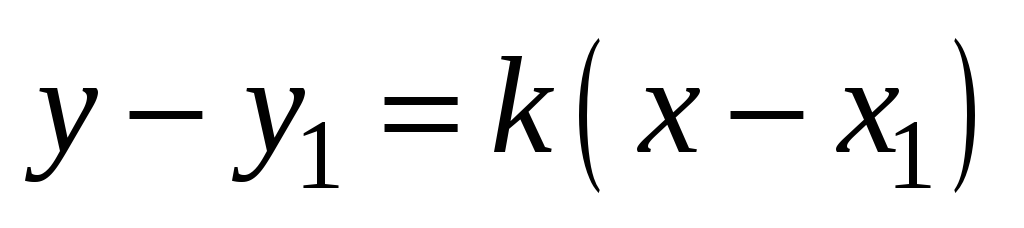
   и условием перпендикулярности двух
   прямых
   :

Определим угловой коэффициент прямой
ВС. Для этого разрешим уравнение стороны
ВС относительно у:

Следовательно, высота, проведённая из
точки А, имеет угловой коэффициент

Тогда, уравнение высоты, опущенной из
вершины А(-8;3) на сторону ВС:

1. Найдём длину высоты, проведённой из
   вершины А. Она равна расстоянию от точки
   А(-8;3) до прямой ВС заданной уравнением
   .
   По формуле
   
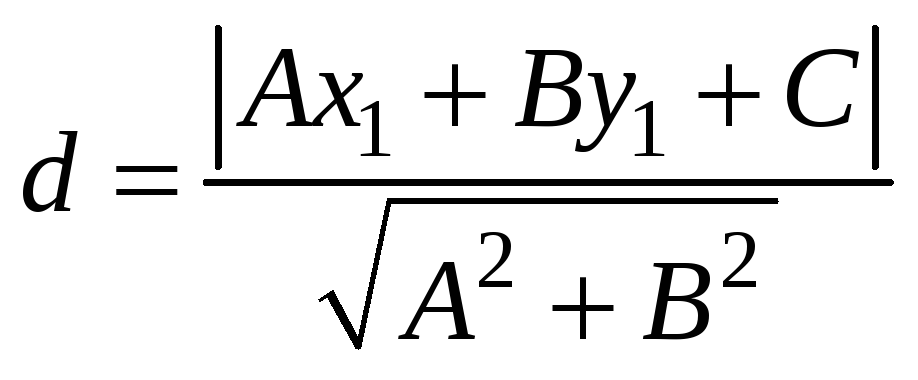
   вычисляем расстояние от точки А до
   прямой ВС, полагая
   

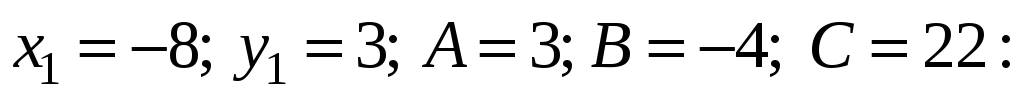
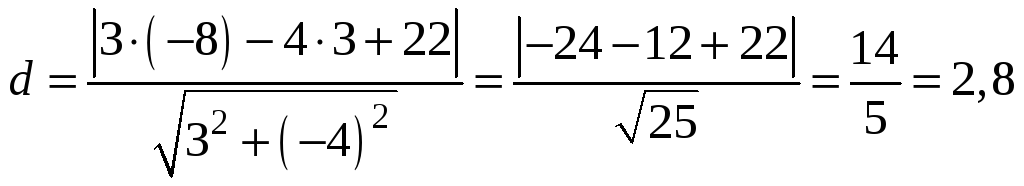
1. Найдём угол В. Угол В равен углу между
   прямыми ВС и АВ и может быть найден с
   помощью формулы
   .
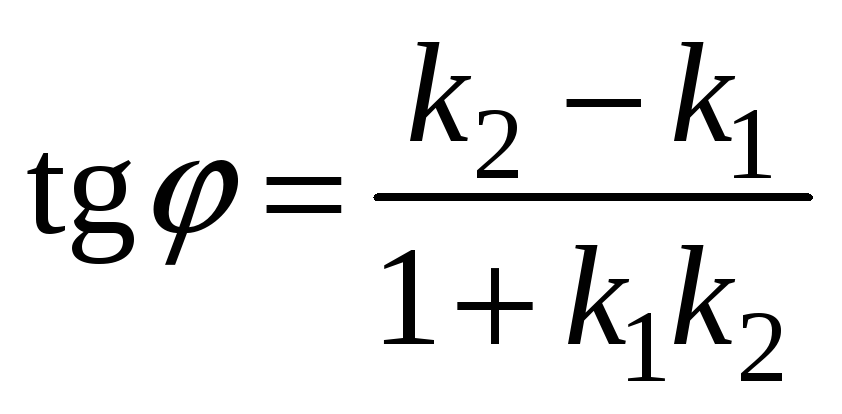   Угловой коэффициент прямо ВС известен
   и равен
   .
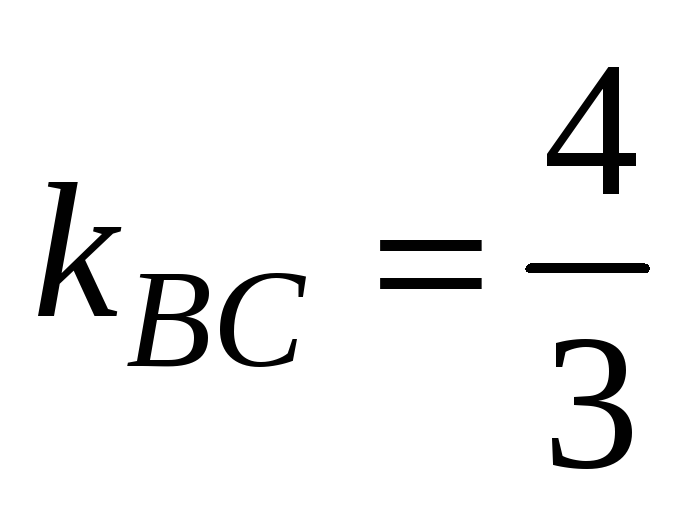   Найдём угловой коэффициент прямой АВ
   по формуле:
   

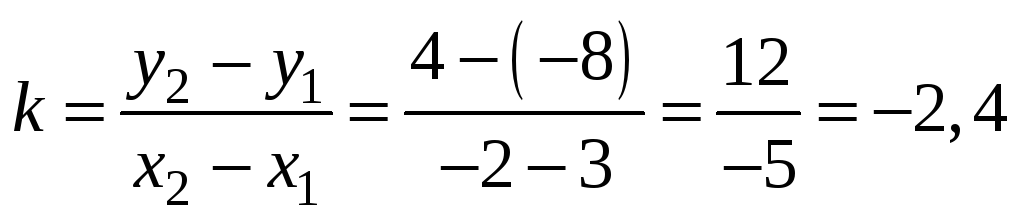
Тогда получаем,

И угол равен

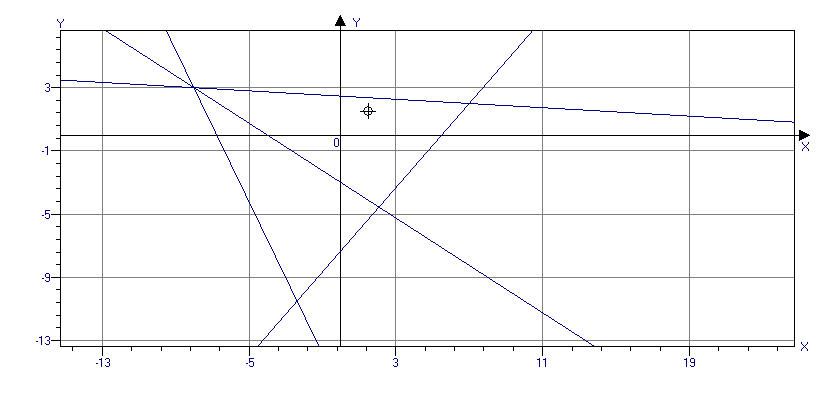
Выполним чертёж. В прямоугольной
декартовой системе координат хОу строим
исходные точки и получаем треугольник
АВС. Затем из вершины А опустим
перпендикуляр на сторону ВС, получим
АК.

18

Даны координаты вершин пирамиды А₁А₂А₃А₄.
Найти:

1. координаты вектора
   
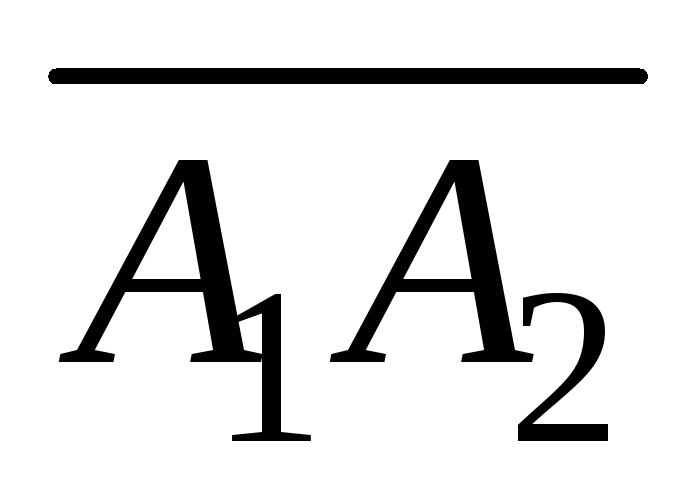
   и длину ребра
   ;

2. угол между рёбрами
   
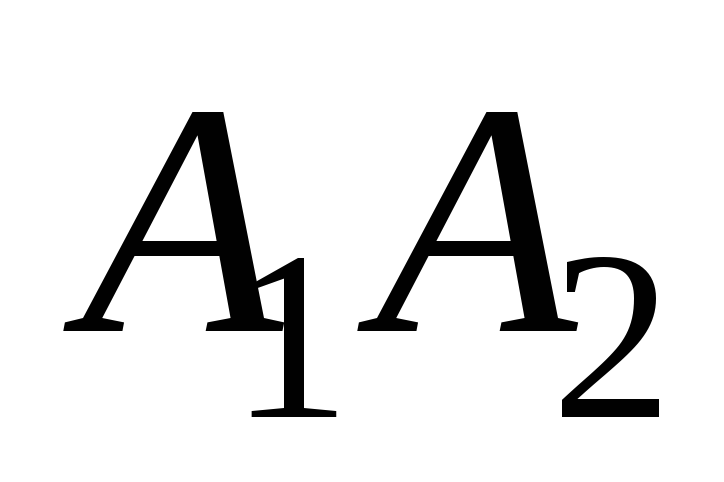
   и
   ;

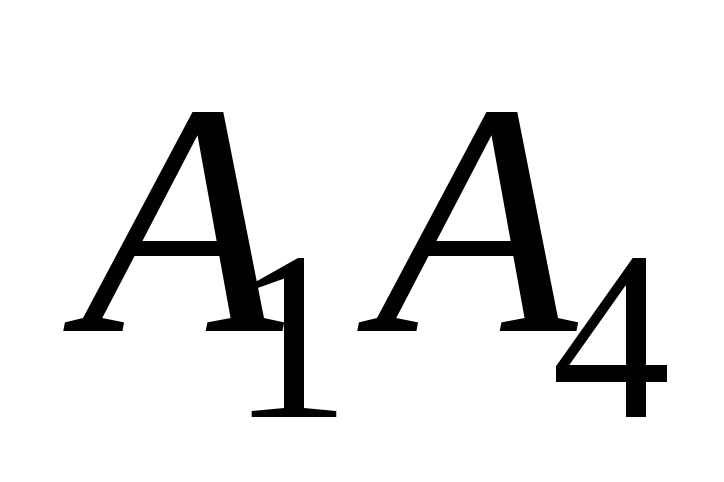3. площадь грани
   ;

4. объём пирамиды;

5. уравнение плоскости
   ;

6. уравнение прямой
   ;

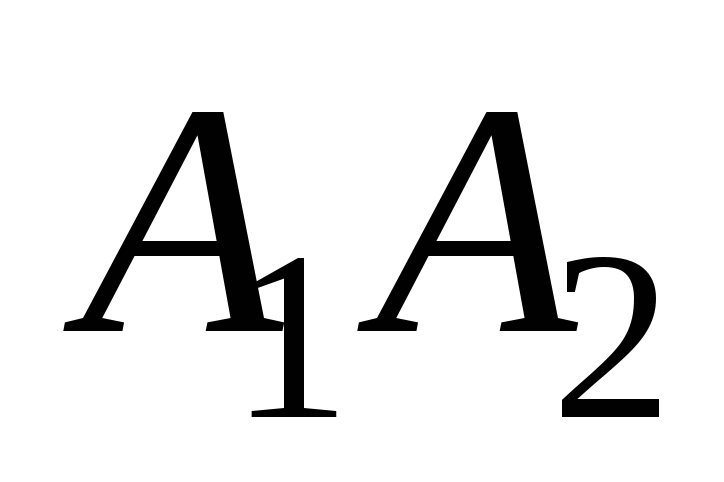7. угол между ребром
   
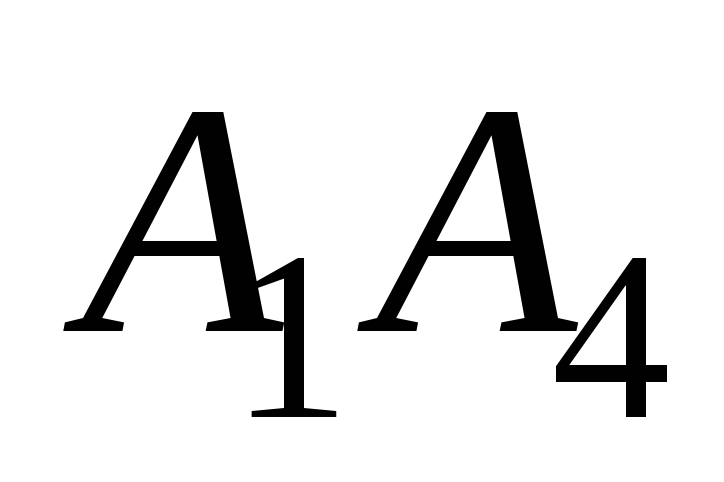
   и гранью
   ;

8. уравнение высоты, опущенной из вершины
   
   на грань
   ;

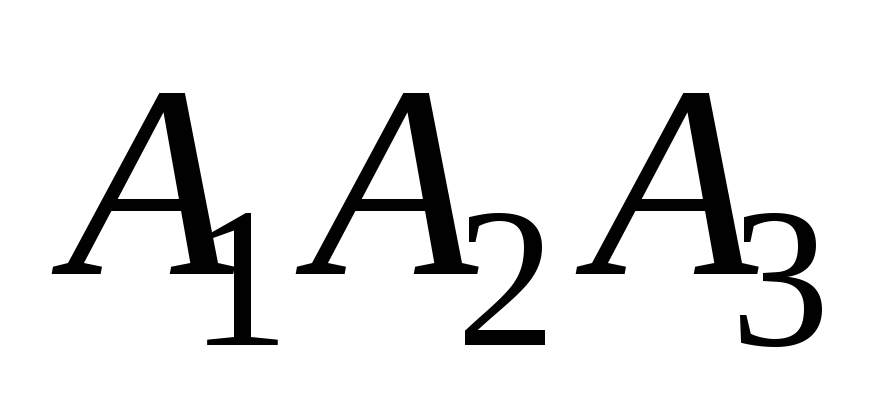Сделать чертёж.

Дано: А₁(7;2;2), А₂(5;7;7), А₃(5;3;1),
А₄(2;3;7).

РЕШЕНИЕ

1. Вектор
   
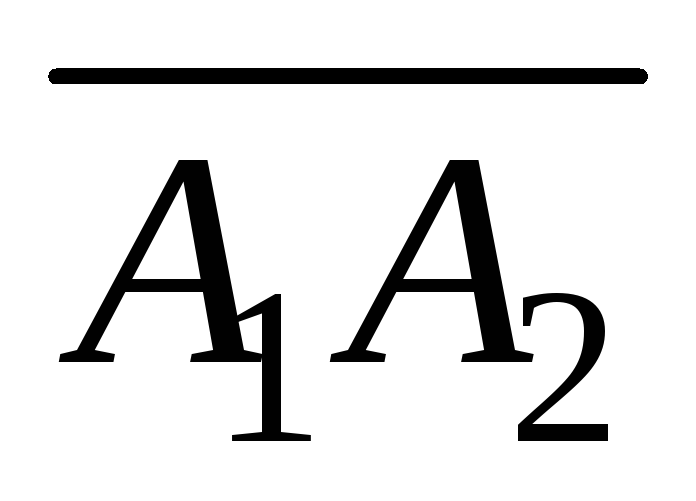
   равен

Длину ребра

можно найти как расстояние между двумя
точками

и
,
оно равно

Получаем

1. Угол между рёбрами
   
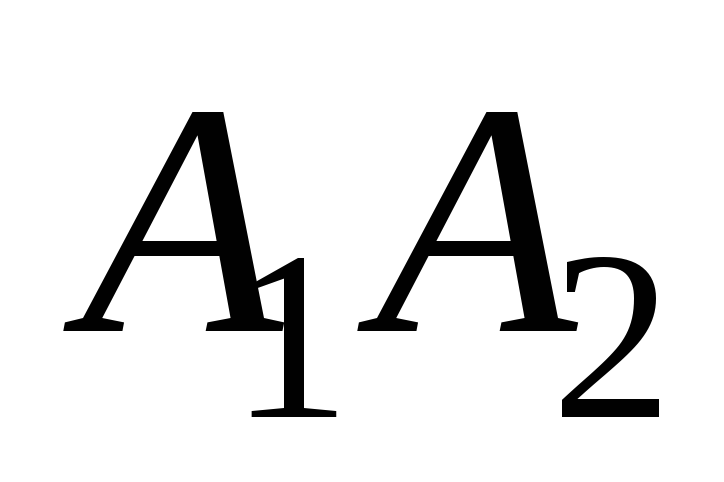
   и
   
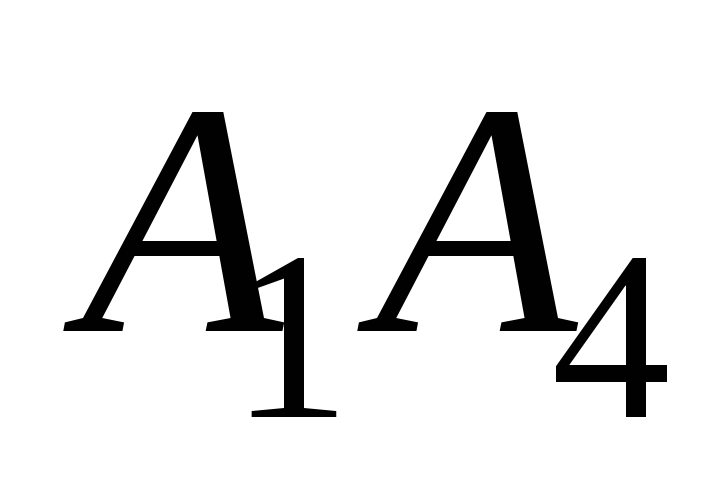
   найдём как угол между векторами
   
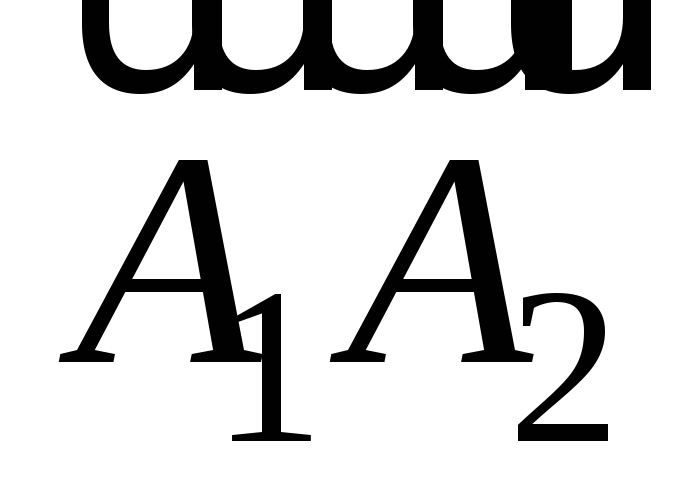
   и
   .

Вектор

Таким образом, имеем два вектора

и
,
угол между ними найдём по формуле:

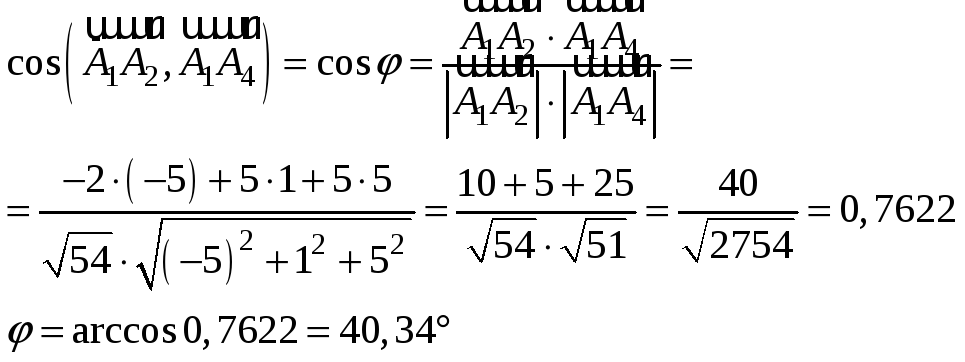
Скалярное произведение двух векторов
в числителе дроби находили как сумму
произведений одноимённых координат
(проекций).

1. Площадь грани
   
   равна половине площади параллелограмма,
   построенного на векторах, как на
   сторонах. И площадь треугольника
   
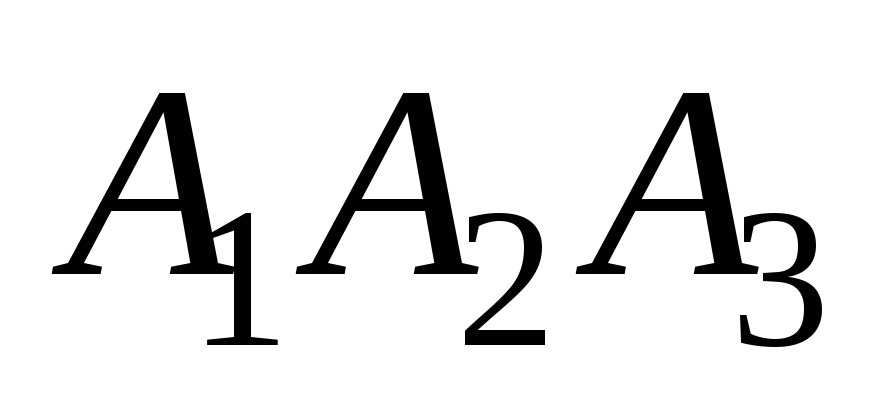
   можно вычислить через векторное
   произведение
   

Координаты вектора

или

Векторное произведение вычислим через
определитель 3-го порядка, разложив его
по элементам первой строки:

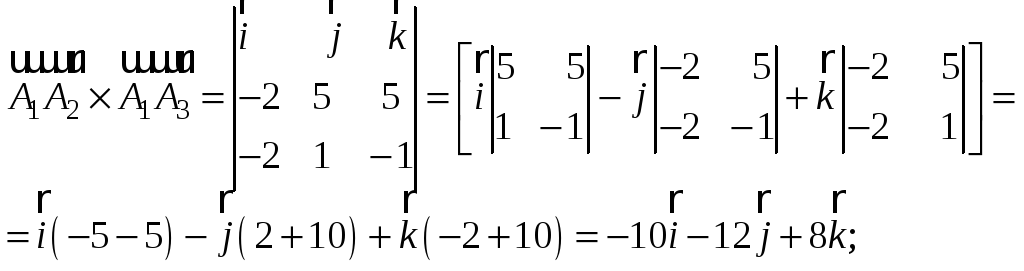
Модуль векторного произведения

1. Объём треугольной пирамиды А₁А₂А₃А₄
   можно рассматривать как одну шестую
   часть объёма параллелепипеда, построенного
   на векторах
   ,
   
   и
   
   как на рёбрах:

Смешанное произведение трёх векторов
равно

1. Уравнение плоскости
   
   имеет вид

или для нашей задачи

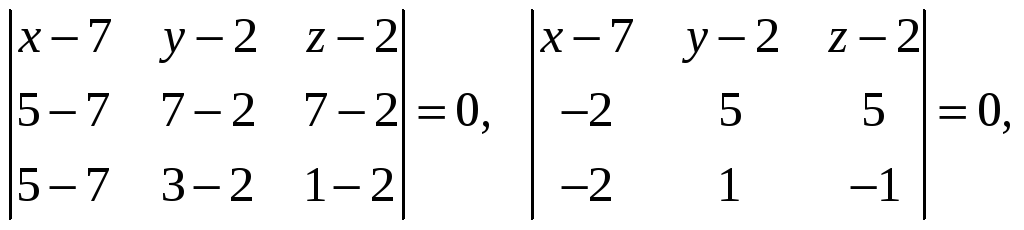
Разложим определитель по элементам
первой строки:

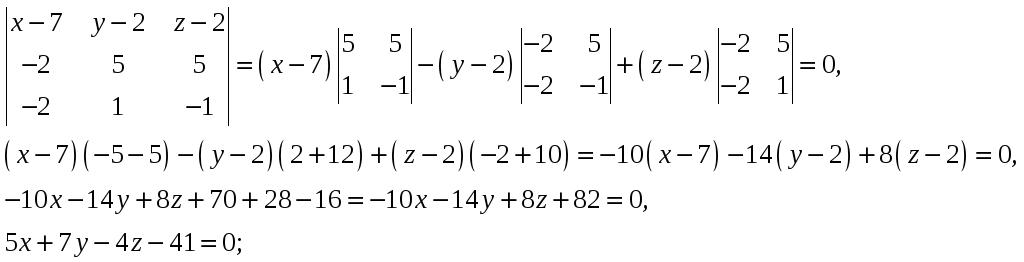
1. Уравнения прямой
   
   найдём в канонической форме, для этого
   воспользуемся уравнением прямой,
   проходящей через две заданные точки
   
   и
   :

,

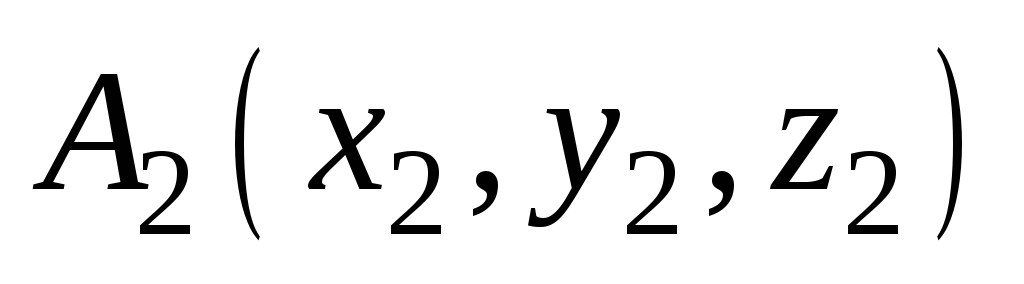1. Углом ψ между ребром
   
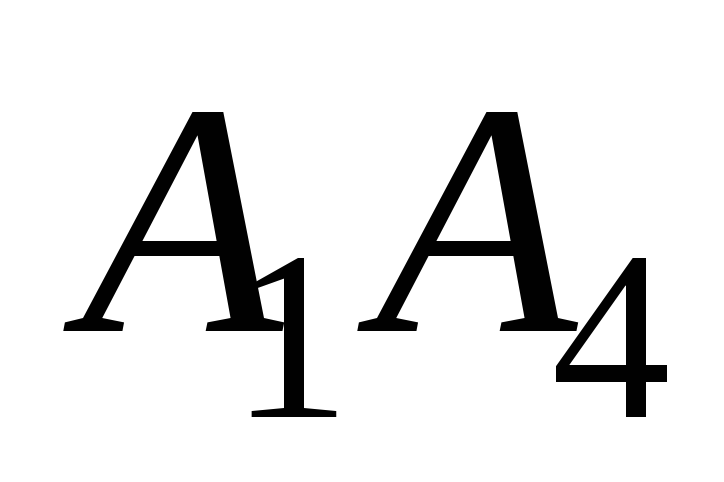
   и гранью
   
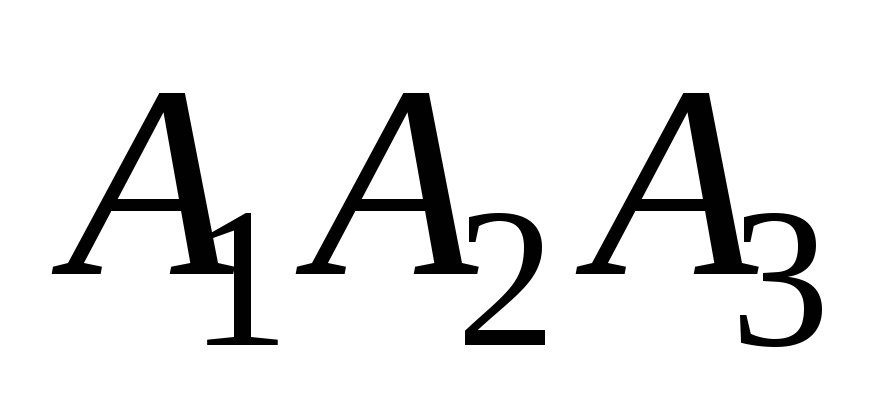
   будет острый угол между прямой
   
   и её проекцией на плоскость
   .
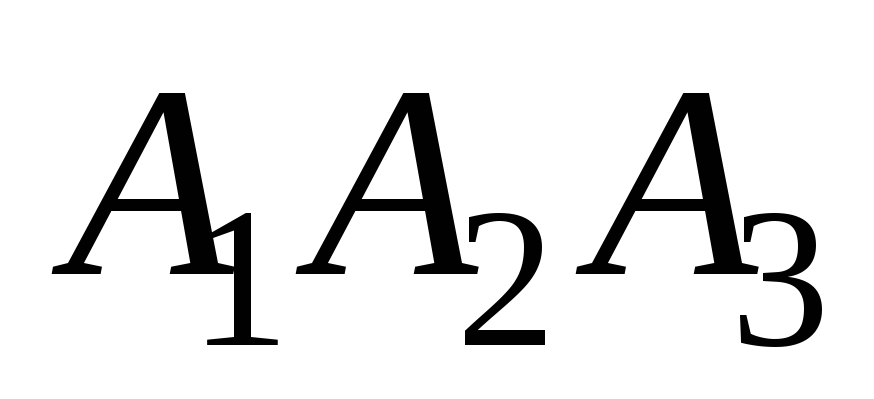   Для нахождения угла ψ воспользуемся
   формулой

Канонические уравнения прямой

получим как:

Отсюда l=5; m=1;
n=-5, где l,
m, n –
координаты направляющего вектора прямой
:

;

Уравнение плоскости

было получено в пункте 5:

Отсюда А=5; В=7; С=-4, где А, В, С – координаты
нормального вектора плоскости
:

Тогда получаем

1. Уравнения высоты, опущенной из вершины
   
   на грань
   .

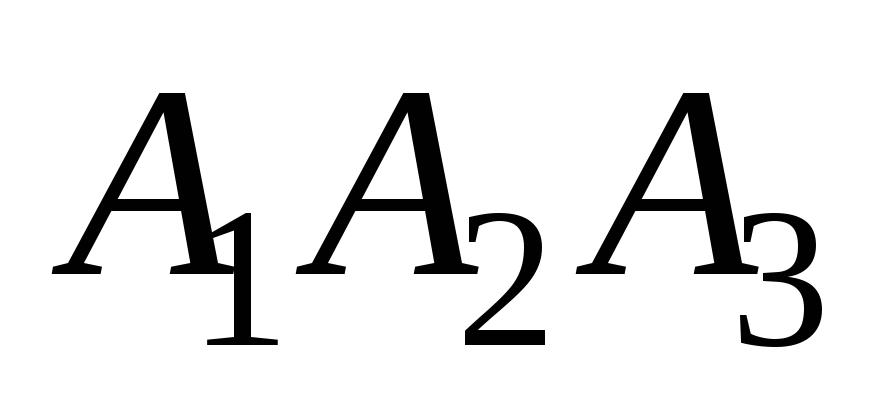Канонические уравнения прямой, проходящей
через точку
,
имеют вид
,
где l, m, n
– координаты направляющего вектора
прямой.

Так как высота перпендикулярна плоскости
,
то из условия перпендикулярности прямой
и плоскости

координаты направляющего вектора
прямой, перпендикулярной плоскости
можно заменить координатами нормального
вектора плоскости l=A=5;
m=B=7; n=C=-4.

Окончательно получим

Выполним чертёж пирамиды как пересечения
плоскостей её граней:

Грань А₁А₂А₄:

Грань А₁А₂А₃:

Грань А₁А₃А₄:

Грань А₂А₃А₄:

28

Составить уравнение и построить линию,
каждая точка которой равноотстоит от
оси ординат и от окружности

РЕШЕНИЕ

В системе координат хОу строим ось
ординат х=0 и окружность

Пусть точка М(х; у) – произвольная точка
искомого геометрического места точек.
Опустим перпендикуляры на ось ординат
и на окружность.

Тогда расстояние от произвольной точки
М(х; у) до оси ординат
–
абсцисса точки М(х; у), а расстояние от
точки М(х; у) до окружности
.
Приравнивая эти расстояния и снимая
знак модуля, получаем

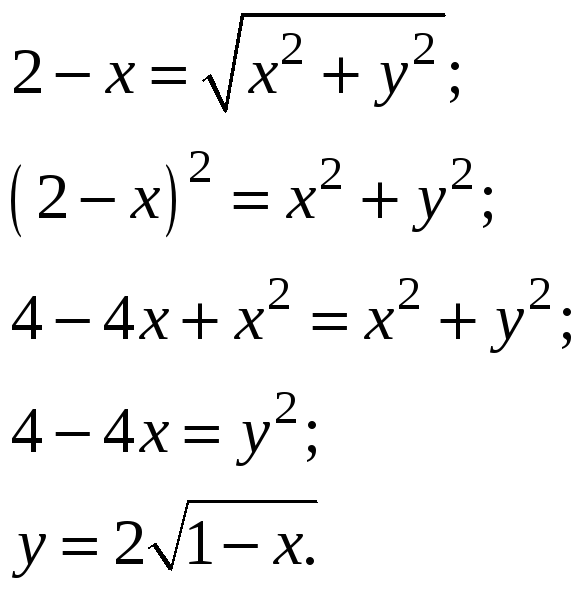
Получили уравнение параболы, строим
верхнюю часть окружности и параболы,
так как чертёж симметричный:

Соседние файлы в папке Приборостроителям

• #
• #
• #
• #
• #
• #
• #
• #
• #