Даны модули векторов как найти скалярное произведение - Сайт, где вы сможете решить свои вопросы

Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.

Скалярное произведение векторов

Формула

Пусть даны векторы $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $. Как найти скалярное произведение векторов? Для того, чтобы найти скалярное произведение векторов необходимо воспользоваться формулой: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y $$ Стоит заметить, что скалярное произведение записывается в скобках, в которых векторы записываются через запятую. Данное обозначение широко применяется в математике и его нужно запомнить.

Если в задаче векторы заданы тремя координатами (в пространстве), то найти скалярное произведение векторов нужно по другой формуле, основанной на предыдущей. Но с тем же смыслом: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z $$

По сути скалярное произведение – это сумма произведений соответствующих координат данных векторов. Первая координата умножается на первую, вторая на вторую и затем произведения суммируются.

Примеры решений

Пример 1

Найти скалярное произведение векторов $ overline{a} = (-1;2) $ и $ overline{b} = (2;1) $

Решение

В данном примере векторы заданы двумя координатами, поэтому применяем первую формулу для плоской задачи. Умножаем соответствующие координаты, а потом складываем их:

$$ (overline{a},overline{b}) = -1 cdot 2 + 2 cdot 1 = -2 + 2 = 0 $$

Произведение получилось равным нулю, а это кстати означает, что векторы оказались ортогональными (перпендикулярными) друг к другу.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ (overline{a},overline{b}) = 0 $$

Пример 2

В пространстве заданы начала и концы векторов: $$ A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2) $$ Требуется найти скалярное произведение векторов $ overline{AB} $ и $ overline{AC} $.

Решение

В примеры решения данной задачи даны только точки и сразу вычислить произведение векторов не представляется возможным. Сначала нужно найти сами векторы $ overline{AB} $ и $ overline{AC} $. Вычисляются они с помощью разности соответствующих координат точек (из конца вычитается начало вектора):

$$ overline{AB} = (-1 – 1; 4-3; 1-(-2)) = (-2; 1; 3) $$

$$ overline{AC} = (2 – 1; 1 – 3; -2 – (-2)) = (1; -2; 0) $$

Теперь, когда необходимые векторы найдены, то вычисляем их произведение:

$$ (overline{AB},overline{AC}) = -2 cdot 1 + 1 cdot (-2) + 3 cdot 0 = -2-2+0 = -4 $$

Ответ

$$ (overline{AB},overline{AC}) = -4 $$

В статье мы ответили на вопрос: «Как найти скалярное произведение векторов?», а так же привели формулы и примеры решений задач.

Источник

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В случае плоской задачи скалярное произведение векторов a = {a_x ; a_y} и b = {b_x ; b_y} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y

Формула скалярного произведения векторов для пространственных задач

В случае пространственной задачи скалярное произведение векторов a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y + a_z · b_z

Формула скалярного произведения n -мерных векторов

В случае n-мерного пространства скалярное произведение векторов a = {a₁ ; a₂ ; … ; a_n} и b = {b₁ ; b₂ ; … ; b_n} можно найти воспользовавшись следующей формулой:

a · b = a₁ · b₁ + a₂ · b₂ + … + a_n · b_n

Свойства скалярного произведения векторов

Скалярное произведение вектора самого на себя всегда больше или равно нуля:

a · a ≥ 0
Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:

a · a = 0 <=> a = 0
Скалярное произведение вектора самого на себя равно квадрату его модуля:

a · a = |a|²
Операция скалярного умножения коммуникативна:

a · b = b · a
Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:

a ≠ 0, b ≠ 0, a · b = 0 <=> a ┴ b
(αa) · b = α(a · b)
Операция скалярного умножения дистрибутивна:

(a + b) · c = a · c + b · c

Примеры задач на вычисление скалярного произведения векторов

Примеры вычисления скалярного произведения векторов для плоских задач

Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.

Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.

Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.

Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.

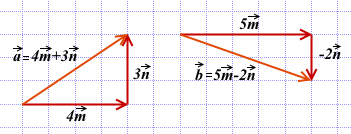
Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a – 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.

Решение:

p · q = (a + 3b) · (5a – 3b) = 5 a · a – 3 a · b + 15 b · a – 9 b · b =

= 5 |a|² + 12 a · b – 9 |b|² = 5 · 3² + 12 · 3 · 2 · cos 60˚ – 9 · 2² = 45 +36 -36 = 45.

Пример 4. Найти скалярное произведение векторов (a + 2i)·(b – 2j),если a = {1; 2} и b = {4; -8}.

Решение: Запишем вектора a и b через ортонормированные базисные вектора i и j:

a = i + 2j
b = 4i – 8j

Тогда используя свойства ортов (i² = 1, j² = 1, i·j = 0)

(a + 2i)·(b – 2j) = (i + 2j + 2i)·(4i – 8j – 2j) = (3i + 2j)·(4i – 10j) = 12i² – 30i·j + 12j·i – 20j² = 12 – 0 + 0 – 20 = -8

Пример вычисления скалярного произведения векторов для пространственных задач

Пример 5. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 – 5 = 15.

Пример вычисления скалярного произведения для n -мерных векторов

Пример 6. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 – 5 -4 = 11.

Источник

Скалярное произведение векторов равно произведению

Скаля́рное произведе́ние (иногда называемое внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат.
Используется в определении длины векторов и угла между ними.

Обычно для скалярного произведения векторов и используется одно из следующих обозначений.

{displaystyle (mathbf {a} ,mathbf {b} )}

{displaystyle mathbf {a} cdot mathbf {b} , {vec {a}}cdot {vec {b}}}

или просто

второе обозначение применяется в квантовой механике для векторов состояния^[1].

В простейшем случае, а именно в случае конечномерного вещественного евклидового пространства, иногда используют «геометрическое» определение скалярного произведения ненулевых векторов и как произведения длин этих векторов на косинус угла между ними^[2]:

{displaystyle (mathbf {a} ,mathbf {b} )=|mathbf {a} ||mathbf {b} |cos(theta ).}

Равносильное определение: скалярное произведение есть произведение длины проекции первого вектора на второй и длины второго вектора (см. рисунок). Если хотя бы один из векторов нулевой, то произведение считается равным нулю^[3].

У понятия скалярного произведения существует также большое количество обобщений для различных векторных пространств, то есть для множеств векторов с операциями сложения и умножения на скаляры^[⇨]. Данное выше геометрическое определение скалярного произведения предполагает предварительное определение понятий длины вектора и угла между ними. В современной математике используется обратный подход: аксиоматически определяется скалярное произведение, а уже через него — длины и углы^[4]. В частности, скалярное произведение определяется для комплексных векторов, многомерных и бесконечномерных пространств, в тензорной алгебре.

Скалярное произведение и его обобщения играют чрезвычайно большую роль в векторной алгебре, теории многообразий, механике и физике. Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения^[5].

Определение и свойства[править | править код]

Будем говорить, что в вещественном или комплексном векторном пространстве определено скалярное произведение, если каждой паре векторов из поставлено в соответствие число из того числового поля, над которым задано удовлетворяющее следующим аксиомам.

Для любых трёх элементов ${displaystyle mathbf {a} _{1},mathbf {a} _{2},mathbf {b} }$ пространства и любых чисел справедливо равенство: ${displaystyle (alpha mathbf {a} _{1}+beta mathbf {a} _{2},mathbf {b} )=alpha (mathbf {a} _{1},mathbf {b} )+beta (mathbf {a} _{2},mathbf {b} )}$ (линейность скалярного произведения по первому аргументу).
Для любых справедливо равенство , где черта означает комплексное сопряжение.
Для любого имеем: , причём только при (положительная определённость и невырожденность скалярного произведения соответственно).

Заметим, что из аксиомы 2 следует, что — вещественное число. Поэтому аксиома 3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения. Если аксиома 3 не выполняется, то произведение называется индефинитным или неопределённым.

Если не только при , то произведение называется квазискалярным^[6].

Из данных аксиом получаются следующие свойства:

коммутативность для вещественных векторов:

Дистрибутивность скалярного произведения в случае вещественного евклидового пространства
дистрибутивность относительно сложения: и
инволюционная линейность относительно второго аргумента: ${displaystyle (mathbf {a} ,(alpha _{1}mathbf {b} _{1}+alpha _{2}mathbf {b} _{2}))={overline {alpha _{1}}}(mathbf {a} ,mathbf {b} _{1})+{overline {alpha _{2}}}(mathbf {a} ,mathbf {b} _{2});}$ (в случае вещественного — просто линейность по второму аргументу).
(что совпадает с для вещественного ).

Также есть свойства, связанные не с данными аксиомами:

неассоциативность относительно умножения на вектор^[7]‘: ;
ортогональность: два ненулевых вектора a и b ортогональны тогда и только тогда, когда (a, b) = 0 (определения ниже).

Замечание. В квантовой физике скалярное произведение (волновых функций, которые комплекснозначны) принято определять как линейное по второму аргументу (а не по первому), соответственно, по первому аргументу оно будет инволюционо линейным. Путаницы обычно не возникает, поскольку традиционное обозначение для скалярного произведения в квантовой физике также отличается: , т.е. аргументы отделяются вертикальной чертой, а не запятой, и скобки всегда угловые.

Определение и свойства в евклидовом пространстве[править | править код]

Вещественные векторы[править | править код]

В -мерном вещественном евклидовом пространстве векторы определяются своими координатами — наборами вещественных чисел в ортонормированном базисе. Определить скалярное произведение векторов ${displaystyle mathbf {a} =(a_{1},a_{2}dots a_{n}),mathbf {b} =(b_{1},b_{2}dots b_{n})}$ можно так^[4]:

${displaystyle langle mathbf {a} ,mathbf {b} rangle =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+dots +a_{n}b_{n}.}$

Проверка показывает, что все три аксиомы выполнены.

Например, скалярное произведение векторов и будет вычислено так:

${displaystyle {begin{aligned} (1,3,-5)cdot (4,-2,-1)&=1cdot 4+3cdot (-2)+(-5)cdot (-1)\&=4-6+5\&=3.end{aligned}}}$

Можно доказать^[8], что эта формула равносильна определению через проекции или через косинус:

Комплексные векторы[править | править код]

Для комплексных векторов ${displaystyle mathbf {a} =(a_{1},a_{2}dots a_{n}),mathbf {b} =(b_{1},b_{2}dots b_{n})}$ определим аналогично^[9]:

${displaystyle langle mathbf {a} ,mathbf {b} rangle =sum _{k=1}^{n}a_{k}{overline {b_{k}}}=a_{1}{overline {b_{1}}}+a_{2}{overline {b_{2}}}+cdots +a_{n}{overline {b_{n}}}.}$

Пример (для n=2 ):

Свойства[править | править код]

Помимо общих свойств скалярного произведения, для многомерных евклидовых векторов верно следующее:

в отличие от обычного умножения скаляров, где если ab = ac и a ≠ 0, то b равняется c, для скалярного умножения векторов это неверно: если a · b = a · c, то есть a · (b − c) = 0, то в общем случае a и b − c лишь ортогональны; но вектор b − c в общем случае не равен 0, то есть b ≠ c;
правило произведения: для дифференцируемых вектор-функций a(t) и b(t) верно соотношение (a(t), b(t))′ = a′(t) ⋅ b(t) + a(t) ⋅ b′(t)^[10];
оценка угла между векторами:

в формуле знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение больше 0, если угол между векторами острый, и меньше 0, если угол между векторами тупой;
проекция вектора на направление, определяемое единичным вектором :

${displaystyle a_{e}=(mathbf {a} ,mathbf {e} )=|mathbf {a} ||mathbf {e} |cos angle {(mathbf {a} ,mathbf {e} )}=|mathbf {a} |cos angle {(mathbf {a} ,mathbf {e} )}}$ , так как
площадь параллелограмма, натянутого на два вектора и , равна ${displaystyle {sqrt {(mathbf {a} ,mathbf {a} )(mathbf {b} ,mathbf {b} )-(mathbf {a} ,mathbf {b} )^{2}}}.}$

Теорема косинусов в вещественном пространстве[править | править код]

Теорема косинусов легко выводится с использованием скалярного произведения. Пусть на сторонах треугольника находятся векторы a, b и c, первые два из которых образуют угол θ, как показано в изображении справа. Тогда, следуя свойствам и определению скалярного произведения через косинус:

${displaystyle {begin{aligned}mathbf {color {orange}c} cdot mathbf {color {orange}c} &=(mathbf {color {red}a} -mathbf {color {blue}b} )cdot (mathbf {color {red}a} -mathbf {color {blue}b} )\&=mathbf {color {red}a} cdot mathbf {color {red}a} -mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {blue}b} cdot mathbf {color {red}a} +mathbf {color {blue}b} cdot mathbf {color {blue}b} \&=|mathbf {color {red}a} |^{2}-mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {red}a} cdot mathbf {color {blue}b} +|mathbf {color {blue}b} |^{2}\&=|mathbf {color {red}a} |^{2}-2mathbf {color {red}a} cdot mathbf {color {blue}b} +|mathbf {color {blue}b} |^{2}\&=|mathbf {color {red}a} |^{2}+|mathbf {color {blue}b} |^{2}-2|mathbf {color {red}a} |{cdot }|mathbf {color {blue}b} |cos mathbf {color {purple}theta } .\end{aligned}}}$

Связанные определения[править | править код]

В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия^[11]:

Длина вектора, под которой обычно понимается его евклидова норма:

{displaystyle |mathbf {a} |={sqrt {(mathbf {a} ,mathbf {a} )}}}

(термин «длина» обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).

Углом varphi между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):

${displaystyle cos varphi ={frac {(mathbf {a} ,mathbf {b} )}{|mathbf {a} ||mathbf {b} |}} (0leqslant varphi leqslant pi ).}$

Данные определения позволяют сохранить формулу: и в общем случае. Корректность формулы для косинуса гарантирует неравенство Коши — Буняковского^[12]:

Для любых элементов векторного пространства со скалярным произведением выполняется неравенство:

${displaystyle vert (mathbf {a} ,mathbf {b} )vert ^{2}leqslant (mathbf {a} ,mathbf {a} )(mathbf {b} ,mathbf {b} )}$

В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):

{displaystyle |(mathbf {a} ,mathbf {b} )|=|mathbf {a} ||mathbf {b} |operatorname {ch} varphi .}

Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.
- При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.

История[править | править код]

Скалярное произведение было введено У. Гамильтоном в 1846 году^[13] одновременно с векторным произведением в связи с кватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю^[14].

Вариации и обобщения[править | править код]

В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных или комплексных функций можно ввести положительно определённое скалярное произведение:

${displaystyle (mathbf {f} ,mathbf {g} )=int limits _{Omega }f(x){overline {g(x)}}dOmega }$

При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора^[15] $g_{ij}$ :

${displaystyle (mathbf {a} ,mathbf {b} )=g_{ij}a^{i}b^{j}}$

При этом сама метрика (говоря точнее, её представление в данном базисе) так связана со скалярными произведениями базисных векторов $f_{i}$ :

${displaystyle g_{ij}=(mathbf {f} _{i},mathbf {f} _{j})}$

Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:

${displaystyle (mathbf {f} ,mathbf {g} )=int limits _{(Omega _{1}times Omega _{2})}K(x_{1},x_{2})f(x_{1})g(x_{2})d(Omega _{1}times Omega _{2})}$

${displaystyle (mathbf {f} ,mathbf {g} )=int limits _{Omega }K(x)f(x)g(x)dOmega }$

где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).

Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам.

См. также[править | править код]

Гильбертово пространство
Векторное произведение
Внешнее произведение
Псевдоскалярное произведение
Смешанное произведение

Примечания[править | править код]

↑ Hall B. C. Quantum Theory for Mathematicians. — NY: Springer Science & Business Media, 2013. — xvi + 553 p. — (Graduate Texts in Mathematics. Vol. 267). — ISBN 978-1-4614-7115-8. Архивная копия от 31 января 2016 на Wayback Machine — P. 85.
↑ Имеется в виду наименьший угол между векторами, не превосходящий
↑ Векторная алгебра // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 634.
↑ ¹ ² Гельфанд, 1971, с. 30—31.
↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193—194. — 704 с. — ISBN 5-85270-087-8.
↑ Кудрявцев Л. Д. Математический анализ. II том. — М., Высшая школа, 1970. — с. 316.
↑ Weisstein, Eric W. Dot Product Архивная копия от 29 апреля 2021 на Wayback Machine. From MathWorld — A Wolfram Web Resource.
↑ Calculus II – Dot Product. tutorial.math.lamar.edu. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
↑ Гельфанд, 1971, с. 86.
↑ Stewart, James (2016), Calculus (8 ed.), Cengage, Section 13.2.
↑ Гельфанд, 1971, с. 34.
↑ §9.5. Линейные пространства со скалярным произведением: евклидовы и унитарные
↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101. Архивная копия от 6 марта 2019 на Wayback Machine
↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
↑ Гельфанд, 1971, с. 240.

Литература[править | править код]

Гельфанд И. М. Лекции по линейной алгебре. — 4-е изд. — М.: Наука, 1971. — 272 с.

Ссылки[править | править код]

Емелин А. Скалярное произведение векторов. Дата обращения: 14 ноября 2019.

Источник

Что такое произведение векторов

Определение

Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.

Это одна из основных операций над векторами в векторной алгебре. Вектор, в отличие от обычного отрезка, имеет не только длину, но и направление в пространстве.

Основные типы перемножения векторов

В математике есть два основных вида умножения векторов: скалярное и векторное. Результатом первого является число, результатом второго — вектор. Оба произведения применяются к двум векторам. Также выделяют смешанное произведение векторов, которое является комбинацией двух вышеописанных. Оно применяется, когда необходимо узнать результат умножения трех векторов.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Скалярное

Определение

Скалярным произведением двух векторов называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними. Длина вектора является его модулем.

Записывается скалярное произведение двумя способами: ( (overline a,;overline b) ) или ( overline acdotoverline b.)

Алгебраические свойства скалярного произведения

Перестановочность. Произведение не меняется от перемены мест множителей: (overline acdotoverline b=overline bcdotoverline a.)
Сочетательность относительно числа. Умножение одного из векторов на число равносильно умножению обоих векторов на это число: ((lambdaoverline a)cdotoverline b=lambda(overline acdotoverline b)(lambdaoverline a)cdot(muoverline b)=(lambdamu)(overline acdotoverline b).)
Распределительный закон. Скалярное произведение суммы двух векторов на третий равносильно сумме скалярных произведений этих векторов на третий вектор: ((overline a+overline b)cdotoverline c=overline acdotoverline c+overline bcdotoverline c.)

Примечание

Таким образом, при выполнении алгебраических действий, связанных со скалярным произведением, с векторами можно обращаться как с числами.

Геометрические свойства скалярного умножения

Скалярное произведение вектора на него же равняется квадрату его модуля: (overline acdotoverline a=overline a^2=overline{left|aright|}cdotoverline{left|aright|}cdotcosleft(0right)=left|overline a^2right|.)
Если угол между векторами острый (меньше (90^circ)), то скалярное произведение этих векторов больше нуля.
Если угол между векторами тупой (больше (90^circ)), то их скалярное произведение меньше нуля.
Если вектора перпендикулярны (угол равен (90^circ)), то их скалярное произведение будет равняться нулю.
Если координаты перемножаемых векторов известны, то их скалярное произведение будет равняться сумме произведений соответствующих координат:( overline acdotoverline b=a_xcdot b_x+a_ycdot b_y+a_zcdot b_z.)

Геометрический смысл

Скалярное произведение двух векторов равно произведению модуля одного из них на проекцию второго вектора на первый.

(overline acdotoverline b=left|overline aright|cdot пр_overline aoverline b=overline{left|bright|}cdot пр_overline boverline a)

(пр_overline boverline a=frac{overline acdotoverline b}{left|overline bright|})

Физический смысл

Скалярное произведение применяется для расчета работы, выполняемой при перемещении материальной точки вдоль вектора (overline s) под действием силы (overline F), приложенной под некоторым углом (varphi.)

Физический смысл скалярного произведения

Рисунок 1. Физический смысл скалярного произведения

Силу (overline F) необходимо разложить на ортогональные компоненты (overline{F_1}) и (overline{F_2}.) Тогда (overline{F_1}) будет являться проекцией силы (overline F) на вектор (overline s:)

(left|overline{F_1}right|=left|overline Fright|cdotcosleft(varphiright).)

В свою очередь, работа A вычисляется по формуле:

(A=left|overline{F_1}right|cdotleft|overline Sright|.)

Соединив данные формулы получим:

(A=left|overline Fright|cdotleft|overline Sright|cdotcosleft(varphiright),)

что является скалярным произведением векторов (overline F) и (overline s:)

(A=overline Fcdotoverline S.)

Векторное

Определение

Векторным произведением векторов overline a и overline b называют перпендикулярный им вектор overline c из правой тройки, модуль которого равняется произведению модулей векторов overline a и overline b на синус угла между ними.

Упорядоченная тройка некомпланарных векторов называется правой, если с конца третьего вектора кратчайший поворот от первого ко второму совершается против часовой стрелки. В противном случае такая тройка называется левой.

Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Векторное произведение может выражаться в записи двумя способами: (overline atimesoverline b) и (lbrackoverline a,overline brbrack.)

Алгебраические свойства

Антиперестановочность. В отличие от скалярного произведения, в векторном при перемене мест множителей знак меняется на противоположный: (overline atimesoverline b=-(overline btimesoverline a))
Сочетательность относительно числа. Как и в случае со скалярным умножением, произведение числа на один из векторов равняется произведению его на другой или на оба вектора: ((lambdaoverline a)timesoverline b=overline atimes(lambdaoverline b)=lambda(overline atimesoverline b).)
Распределительный закон. Векторное произведение суммы двух векторов на третий равносильно сумме векторных произведений этих векторов на третий вектор: ((overline a+overline b)timesoverline c=overline atimesoverline c+overline btimesoverline c.)

Из этого следует, что при выполнении алгебраических действий, связанных с векторным произведением, скобки можно раскрывать так же, как при работе с числами, с поправкой на правило антиперестановочности.

Геометрические свойства

Если вектора (overline a) и (overline b) параллельны, то их векторное произведение равняется нулю.
Векторное произведение векторов с известными координатами выражается в матричном виде: (overline atimesoverline b=begin{vmatrix}i&j&k\a_x&a_y&a_z\b_x&b_y&b_zend{vmatrix}=left(begin{vmatrix}a_y&a_z\b_y&b_zend{vmatrix};;-begin{vmatrix}a_x&a_z\b_x&b_zend{vmatrix};;begin{vmatrix}a_x&a_y\b_x&b_yend{vmatrix}right).)

Геометрический смысл

Модуль векторного произведения двух векторов равняется площади параллелограмма, сторонами которого являются эти вектора.

Геометрический смысл векторного произведения

Рисунок 2. Геометрический смысл векторного произведения

Из определения векторного умножения следует, что модуль полученного вектора равняется произведению модулей исходных векторов на синус угла между ними:

Площадь параллелограмма вычисляется так:

(S=left|overline aright|cdot h, где h=left|overline bright|cdotsinleft(varphiright).)

Таким образом, получаем:

Отсюда следует формула для площади треугольника:

(S_bigtriangleup=frac12left|overline atimesoverline bright|)

Физический смысл

В физике векторное произведение применяется для расчета момента силы, приложенной к одной точке относительно другой:

(overline M=overline{AB}timesoverline F)

Смешанное умножение векторов

Фактически, смешанное произведение векторов представляется как скалярное умножение одного вектора на векторное произведение двух других. Результатом смешанного произведения является число.

Свойства смешанного умножения

((overline atimesoverline b)cdotoverline c=overline acdot(overline btimesoverline c)=overline acdotoverline bcdotoverline c.)
Если (overline acdotoverline bcdotoverline c) больше нуля, тройка векторов — правая.
Если( overline acdotoverline bcdotoverline c) меньше нуля, тройка векторов — левая.
Если вектора (overline a, overline b) и (overline c) компланарны, то их смешанное произведение равняется нулю.

Геометрический смысл

Если вектора overline a, overline b и overline c не компланарны, то их смешанное произведение равно объему параллелепипеда, построенного на этих векторах. Число будет положительным, если тройка векторов правая, и отрицательным, если тройка левая.

(V_{пар.}=overline acdotoverline bcdotoverline c)

Следствием этого является формула нахождения объема пирамиды:

(V_{пир.}=frac16left(overline acdotoverline bcdotoverline cright))

Произведение векторов, примеры и решения

Задача №1

Даны вектора (overline a=(-1,;0,;3) и overline b=(2,;-3,;1).)

Найти их скалярное произведение.

Решение

Возьмем формулу скалярного произведения для векторов с известными координатами:

(overline acdotoverline b=a_xcdot b_x+a_ycdot b_y+a_zcdot b_z) и подставим имеющиеся значения:

(overline acdotoverline b=(-1)cdot2+0cdot(-3)+3cdot1=1)

Задача №2

Найти площадь треугольника с известными координатами угловых точек

Задача №2

Координаты точек: (A(-1,;2,;3), B(0,;-2,;1), C(1,;2,;1))

Решение

Для решения этой простейшей задачи из геометрии воспользуемся следствием геометрического смысла векторного произведения:

(S_bigtriangleup=frac12left|overline atimesoverline bright|)

В данном случае треугольник построен на векторах( overline{AB}) и (overline{AC}). Чтобы рассчитать их координаты, необходимо вычесть из координат конечной точки координаты начальной:

(overline{AB}=(0-(-1),;(-2)-2,;1-3)=(1,;-4,;-2))

(overline{AC}=(1-(-1),;2-2,;1-3)=(2,;0,;-2))

Векторное произведение векторов с известными координатами выполняется в матричном виде:

(overline atimesoverline b=begin{vmatrix}i&j&k\a_x&a_y&a_z\b_x&b_y&b_zend{vmatrix}=left(begin{vmatrix}a_y&a_z\b_y&b_zend{vmatrix};;-begin{vmatrix}a_x&a_z\b_x&b_zend{vmatrix};;begin{vmatrix}a_x&a_y\b_x&b_yend{vmatrix}right))

Подставляем значения векторов( overline{AB}) и (overline{AC}) в матрицу и производим вычисления:

(overline{AB}timesoverline{AC}=begin{vmatrix}i&j&k\1&-4&-2\2&0&-2end{vmatrix}=left(ibegin{vmatrix}-4&-2\0&-2end{vmatrix};;-jbegin{vmatrix}1&-2\2&-2end{vmatrix};;kbegin{vmatrix}1&-4\2&0end{vmatrix}right)=8i-2j+8k)

Подставляем полученное значение в формулу вычисления площади треугольника, учитывая, что в ней фигурирует модуль произведения:

(S_bigtriangleup=frac12left|overline{AB}timesoverline{AC}right|=frac12sqrt{8^2+{(-2)}^2+8^2}=sqrt{132}=11.49)

Источник

Определение 1

Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними.

где

(0°≤φ≤180°).

Если хотя бы один из векторов нулевой, то скалярное произведение принимают равным нулю.

Определение 2

Скалярным произведением двух векторов

называется сумма произведений их соответствующих координат:

(В учебнике в качестве определения даётся одно, другое доказывается как теорема).

Свойства скалярного произведения:

(переместительное);

(сочетательное);

(распределительное);

$[ 4)overrightarrow a cdot overrightarrow a = overrightarrow a ^2 = left| {overrightarrow a } right|^2 ]$

— такое произведение называется скалярным квадратом вектора a.

Из определения следует формула для нахождения угла между ненулевыми векторами:

$[ cos varphi = frac{{overrightarrow a cdot overrightarrow b }}{{left| {overrightarrow a } right| cdot left| {overrightarrow b } right|}}. ]$

Поскольку модуль ненулевого вектора — положительное число, то знаменатель этой дроби — положительное число. Значит знак дроби зависит от знака числителя, то есть от знака скалярного произведения векторов.

Таким образом, знак косинуса угла между векторами совпадает со знаком скалярного произведения векторов.

Поскольку косинус острого угла равен положительному числу, косинус тупого угла равен отрицательному числу, а косинус 90° равен нулю, то

3)Свойство перпендикулярных векторов и признак перпендикулярности векторов:

то есть

Рассмотрим применение скалярного произведения на практике.

№ 1. Найти скалярное произведение векторов

$[1)left| {overrightarrow a } right| = 5,left| {overrightarrow b } right| = 8,angle (overrightarrow a ,overrightarrow b ) = 120^o ;]$

Решение:

подставляем данные из условия и значение cos120°:

$[overrightarrow a cdot overrightarrow b = 5 cdot 8 cdot ( - frac{1}{2}) = - 20.]$

Подставляем координаты векторов:

№ 2. Дано:

$[left| {overrightarrow a } right| = 4,left| {overrightarrow b } right| = 7,angle (overrightarrow a ,overrightarrow b ) = 60^o .]$

Найти:

Решение:

Подставляем данные условия и cos60°

$[ 1)overrightarrow a cdot overrightarrow b = 4 cdot 3 cdot cos 60^o = 12 cdot frac{1}{2} = 6;]$

$[= left| {overrightarrow a } right|^2 + overrightarrow a cdot overrightarrow b = 4^2 + 6 = 22;]$

$[= 5 cdot overrightarrow a cdot overrightarrow b + 2 cdot left| {overrightarrow b } right|^2 = 5 cdot 6 + 7^2 = 79.]$

№ 3. Даны векторы

При каком значении x эти векторы перпендикулярны?

Решение:

Векторы перпендикулярны, если их скалярное произведение равно нулю. Найдём скалярное произведение данных векторов и выясним, при каком значении переменной x оно равно нулю.

Ответ: -6 или 6.

№ 4. Найти косинус угла между векторами

если

Решение:

$[cos angle (overrightarrow a ,overrightarrow b ) = frac{{overrightarrow a cdot overrightarrow b }}{{left| {overrightarrow a } right| cdot left| {overrightarrow b } right|}}.]$