Задача 29832 даны три вектора а=(3,-2,4), в=(5,1,6).
Условие
даны три вектора а=(3,-2,4), в=(5,1,6), с=(-3,0,2) найти вектор х удовлетворяющий трем уравнениям: (а ^ x)=4 (b ^ x)=35 (c ^ x)=0
Все решения
Пусть вектор х имеет координаты (x_(1);x_(2);x_(3)).
Скалярное произведение векторов, заданных своими координатами равно сумме произведений одноименных координат.
Найти четвертую вершину параллелограмма
Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?
В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.
Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.
Дано: ABCD — параллелограмм,
1) Найдём координаты точки O — середины диагонали AC.
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:
Дано: ABCD — параллелограмм,
1) Ищем координаты точки O — середины отрезка BD:
2) Точка O также является серединой AC:
2 Comments
А как вы получили -14 в первом примере.
Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.
3.1.7. Примеры решения задач по теме «Линейные операции над векторами. Скалярное произведение»
Даны векторы А = (-2; 3; 5) и B = (4; -1; 7). Найти координаты вектора
При умножении вектора на число все его координаты
Умножаются на это число, при сложении векторов складываются их соответствующие координаты.
Координаты коллинеарных векторов пропорциональны.
Если A || B, то 
Ответ: 
Найти направляющие косинусы вектора А = <-2; -1; 2>.
Направляющие косинусы являются координатами орта (единичного вектора) данного направления.
Найдем модуль вектора А:
Разделив все координаты вектора А на его модуль, получим координаты орта:
Ответ:
Тогда AA + BB + GC = <2A + B– 3G; –A + B+ G; 3A – B+ 2G>, причем координаты этого вектора должны равняться соответствующим координатам вектора D. Приравнивая эти координаты, получаем систему уравнений для определения A, B, G:
Для векторов A = <1; -2; 3>, B = <-1; 1; -2>, C = <3; 2; 1>, D = < 15; 7; 4>найти такие числа A, B, G, чтобы векторы AA, BB, GC и D образовали замкнутую ломаную линию, если начало каждого последующего вектора совместить с концом предыдущего.
C = <1; -4; 3>линейно зависимой или линейно независимой.
Система векторов называется линейно независимой, если равенство
Вычислим главный определитель Δ системы уравнений
По правилу Крамера система имеет единственное решение, но для однородной системы всегда существует нулевое решение (A = B = G = 0).
Поскольку других решений нет, данная система векторов линейно независима.
Ответ: Система векторов линейно независима.
Найти координаты какого-либо вектора, направленного по биссектрисе угла между векторами А = (-4; 3; 0) и B = (12; -15; 16).
Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.
Вектор A + B направлен по диагонали параллелограмма, построенного на векторах А и B как на смежных сторонах и выходящей из общего начала векторов А и B.
Диагональ параллелограмма является биссектрисой угла между сторонами только в том случае, если этот параллелограмм – ромб. Следовательно, искомым вектором можно считать сумму двух векторов равной длины, коллинеарных соответственно векторам А и B.
Следовательно, |5A| = |B|. Значит, параллелограмм со сторонами, совпадающими с векторами 5A и B, является ромбом, поэтому вектор 5A + B будет иметь заданное направление.
При каких значениях X, Y, Z точки А(Х; -1; 3), В(5; -4; Z), C(-2; Y; 9), D(-5; 1; 7) являются вершинами параллелограмма?
Для выполнения условия задачи требуется коллинеарность векторов 



Для выполнения условия задачи требуется коллинеарность векторов 



Найдем координаты этих векторов:
Из последней пропорции получаем, что Z = 1 – 2Y. Тогда
Но при этих значениях неизвестных
Условие задачи выполнено.
Используйте определение скалярного произведения:
Используем свойства скалярного произведения:
По определению скалярного произведения
Сложим левые и правые части полученных равенств:
Даны векторы А = <2; -3; 1>и B = <-1; 2; 1>. Найти скалярное произведение
Найдите координаты векторов 3А – B и A + 2B или используйте свойства скалярного произведения.
Используем свойства скалярного произведения:
Используйте формулу, выражающую косинус угла между векторами через их скалярное произведение.
Ответ: 
Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.
Координаты вектора B пропорциональны координатам А. Если K – коэффициент пропорциональности, то B = <2K; -2K; 3K>.
Известно, что |A| = 2, |B| = 7. Найти значения K, при которых векторы
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
Если векторы перпендикулярны, то их скалярное произведение равно нулю.
Ответ: K = 
Найти проекцию вектора А = <7; 0; -5>на ось, образующую с координатными осями Ох и Оу углы 60о и 45о, а с осью Oz – тупой угол γ.
Используйте свойство направляющих косинусов:
Найдем cosγ: cos260o + cos245o + cos2γ = 1,
Тогда проекция А на заданную ось равна:
[spoiler title=”источники:”]
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/3-1-7-primery-resheniia-zadach-po-teme-lineinye-operatcii-nad-vektorami-skaliarnoe-proizvedenie
[/spoiler]
Даны три вектора: a={8,4,1}, b={2,-2,1},c={4,0,3}. Найти четвертый вектор d длины 1, перпендикулярный к векторам a и b и направленный так, чтобы упорядоченные тройки векторов a,b,c и a,b,d имели одинаковую ориентацию.
задан
25 Сен ’16 2:59
Jenya
167●1●14
52% принятых
Неизвестный вектор записываем в виде v=(x,y,z). Составляем два уравнения для равенства нулю скалярных произведений. Это даёт однородную систему. Она решается с точностью до коэффициента пропорциональности, который находится далее из соображений длины. Получается два варианта: v и -v. Выбор между ними осуществляется за счёт рассмотрения определителей из координат: по знаку такого определителя распознаётся ориентация.
каждый из следующих векторов: 1).
перпендикулярны, причем
угол
угол
должны удовлетворять векторы
имели место следующие соотношения:
должны удовлетворять векторы
вектор
построить каждый из следующих
векторов:
вектор
и вектор
следующих векторов. Принимая в качестве
масштабной единицы
центром масс треугольника АВС. Доказать, что
пятиугольнике ABCDE заданы векторы, совпадающие с
его ребрами:
ABCDA’B’C’D’ (рис.) заданы векторы, совпадающие с
его ребрами:
каждый из следующих векторов:
;
точке, имеют взаимно перпендикулярные
направления. Определить величину их
равнодействующей
оси следующих векторов:
коллинеарность векторов
3; -9}. Установить, какой из них
длиннее другого и во сколько раз, как они
направлены – в одну или в противоположные
стороны.
каких значениях
четыре точки A(3; -1; 2), B(1; 2; -1), C(2; 2; -7), D(3; -5; 3) служат
вершинами трапеции.
B(5; -7; 8), C(2; 2; -7), D(5; -4; 2). Проверить, что векторы
коллинеарны, установить, какой из
них длиннее другого и во сколько раз, как они
направлены – в одну или в противоположные
стороны.
суммы и разности векторов
1; -4}.
вектора
разложение по этому же базису вектора
вектору
направления, при условии, что
2; -2} приложены к одной точке.
Определить координаты вектора
по биссектрисе угла между векторами
условии, что
2; -2} совпадают со сторонами
теругольника АВС. Определить координаты
векторов, приложенных к вершинам треугольника и
совпадающими с его медианами AM, BN, CP.
– какие угодно неколлинеарные
векторы, то всякий вектор, лежащих в их плоскости,
может быть представлен в виде
что числа
два вектора
базису
три вектора
разложение каждого из этих трех векторов,
принимая в качестве базиса два других.
разложение вектора
базиса векторы
со сторонами треугольника АВС, опреедлить
разложение векторов, приложенных в вершинах
треугольника и совпадающие с его медианами.
етыре точки A(1; -2), B(2; 1), C(3; 2), D(-2; 3). Определить
разложение векторов
принимая в качестве базиса
векторы
некомпланарные векторы, то всякий вектор
может быть представлен в виде
что числа
определяются векторами
вектора
его по базису
разложения.
этих четырех векторов, принимая в качестве
базиса три остальных.
Понятие
вектора
Определение
1. Вектором называется направленный
отрезок ( или, что то же, упорядоченная
пара точек).
Обозначают:
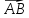
вектора) или одной буквой –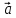
Определение
2. Длиной вектора (модулем)называется
расстояние между началом и концом
вектора. Длина вектора обозначается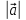
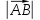
Определение
3. Нулевым вектором называется
вектор, у которого начало и конец
совпадают. Обозначают:
Определение
4. Единичным векторомназывается
вектор, длина которого равна единице.
Единичный
вектор, имеющий одинаковое направление
с данным вектором
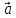
называется ортом вектора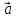
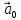
Определение
5. Векторы называютсяколлинеарными,
если они расположены на одной прямой
или на параллельных прямых. Нулевой
вектор считается коллинеарным любому
вектору.
Определение
6. Векторы называютсяравными,
если они коллинеарны, имеют одинаковые
длины и одинаковое направление.
Линейные
операции над векторами
Определение
7. Линейными операциями над вектораминазываются сложение векторов и умножение
вектора на число.
Определение
8. Суммой
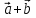
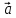

вектор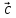
который идет из начала вектора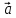
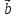
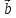
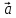
неколлинеарных векторов
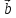
вместо правила треугольника использовать
правило параллелограмма: если векторы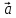
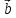
построен параллелограмм, то сумма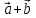
этого параллелограмма, идущего из общего
начала

Определение
9. Разностью
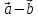
векторов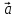
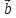
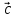
который в сумме с вектором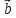
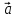
Если два вектора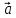
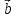
есть вектор, исходящий из конца вектора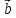

Определение
10. Два коллинеарных вектора равной
длины, направленные в противоположные
стороны, называются противоположными.
Вектор, противоположный вектору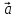
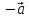
Произведение
вектора
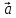
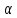
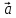
Некоторые
свойства линейных операций
1)
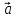
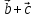
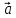
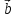
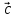
2)
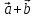
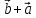
3)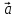
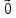

4)
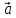
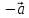
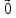
5)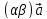

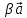
6)
7)

8)
1·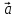
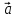
Теорема
1. (О коллинеарных векторах). Если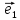

вектор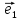
то существует единственное число х
такое, что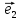
В
частности, ненулевой вектор
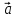
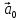

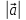
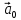
Сформулированные
свойства линейных операций позволяют
преобразовать выражения, составленные
из векторов, по обычным правилам алгебры:
можно раскрыть скобки, приводить подобные
члены, переносить некоторые члены в
другую часть равенства с противоположным
знаком и т.д.
Пример
1.
Доказать
равенства:
а)
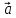
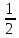


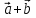
б)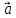
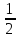

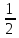
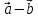
и
выяснить, каков их геометрический смысл.
Решение.
а) В левой части равенства раскроем
скобки, приведем подобные члены, получим
вектор в правой части. Поясним это
равенство геометрически. Пусть даны
два вектора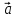
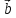
отложим их от общего начала и посмотрим
параллелограмм и его диагонали, получим:
§2 Линейная комбинация векторов
Векторный
базис на плоскости и в пространстве.
Определение
1. Линейной комбинацией векторов
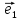
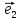
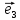
векторов на какие-нибудь числа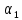
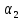

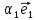
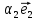
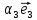
Определение
2. Векторным базисом в данной
плоскости называется любая пара
неколлинеарных векторов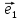
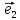
Вектор
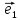
при этом первым базисным вектором,
вектор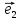
Справедлива
следующая теорема.
Теорема
1.Если базис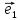
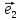
любой вектор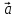
и притом единственным образом, в виде
линейной комбинации базисных векторов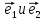
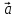
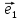
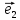
(*)
Определение
3. Равенство(*) называютразложением
вектора
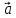
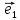
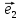
а числа х и у –координатами вектора
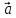
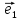
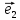
илиотносительно базиса

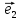
речь, то пишут кратко: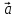
определения координат вектора относительно
базиса следует, что равные векторы имеют
соответственно равные координаты.
Два
и более векторов в пространстве называются
компланарными, если они параллельны
одной и той же плоскости или лежат в
этой плоскости.
Определение
4. Векторным базисом в пространстве
называют любые три вектора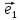

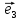
Вектор
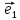
вектором,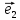
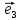
Замечание.
1. Три вектора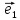
{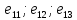
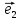
{
и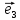

образуют базис пространства, если
определитель, составленный из их
координат, отличен от нуля :

2.
Основные положения теории определителей
и способы их вычисления рассмотрены в
модуле 1 «линейная алгебра».
Теорема
2. Пусть

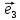
любой вектор
и притом единственным образом, в виде
линейной комбинации базисных векторов
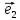
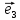
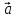
х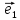
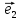
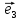
(**)
Определение
5. Равенство (**) называютразложением
вектора

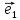
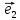

а числаx,y,z–координатами
(компонентами) вектора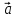
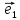
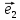
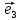
Если
заранее ясно, о каком базисе идет речь,
то пишут кратко:
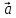
Определение
6. Базис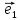
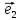
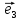
векторы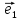
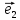
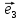
длину. В этом случае приняты обозначения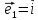
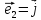
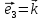
Действия
над векторами, заданными своими
координатами.
Теорема
3. Пусть на плоскости выбран векторный
базис
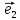
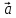
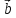
своими координатами: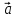

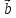
{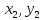
Тогда
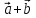
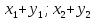
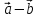
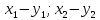
т.е. при сложении или вычитании векторов
складываются или вычитаются их одноименные
координаты;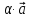
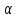
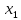
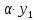
т.е. при умножении вектора на число его
координаты умножаются на это число.
Условие
коллинеарности двух векторов
Теорема
4. Вектор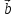
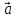
вектора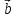
координатам вектора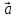
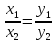
Линейные
операции над векторами, заданными своими
координатами в пространстве, производятся
аналогично.
Пример
1. Пусть даны векторы

= {1;0;1} в некотором векторном базисе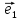

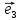
Найти координаты линейной комбинации
2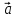
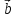
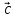
Решение.
Введем обозначение для линейной
комбинации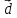
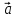

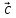
Коэффициенты
линейной комбинации
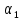
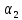

Запишем данное векторное равенство в
координатной форме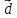
{x,y,z}=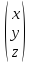
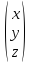
Очевидно,
что каждая координата линейной комбинации
векторов равна такой же линейной
комбинации одноименных координат, т.е.
х
= 2·1+3·3+(-4)·1=7,
у
= 2·2+3·2+(-4)·0=10,
z= 2·(-1)+3·1+(-4)·0=-3.
Координаты
вектора
в базисе
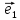
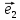
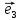

{7,10,-3}
Ответ: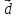
{7,10,-3}.
Общая
(аффинная) декартова система координат
Определение
7. Пусть О- некоторая фиксированная
точка, которую будем называтьначалом.
Если
М- произвольная точка, то вектор
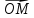
М по отношению к началу, коротко,
радиус-вектор точки М.
Декартовы
(аффинные) координаты на прямой
Пусть
дана в пространстве некоторая прямая
l.Выберем начало
О лежащим на этой прямой. Кроме того,
выберем на прямойl
ненулевой вектор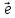
который будем называть базисным.
Определение
8. Пусть точка М лежит на прямойl.
Так как векторы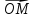
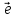
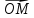

где х- некоторое число. Это число назовемкоординатой точки М на прямой.
Начало
О имеет положительные или отрицательные
координаты, в зависимости от того,
совпадают ли направления векторов
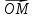
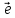
на которой координаты, будем называть
осью координат или осью ОХ.
Введение
координат на прямой соответствует
единственное число х, и наоборот,
существует единственная точка М, для
которой это число является координатой.
Декартовы
(аффинные) координаты на плоскости.
Выберем
на плоскости О два неколлинеарных
вектора
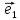
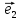
образующих некоторый базис . Очевидно,
что длины векторов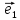
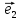
Определение
9. Совокупность {0;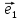
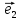
точки О и векторного базиса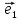

декартовой (аффинной) системой на
плоскости.
Две
прямые, проходящие через О и параллельные
соответственно векторам
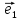
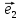
осями координат. Первую из них обычно
называют осью абсцисс и обозначают Ох,
вторую- осью ординат и обозначают Оу.
Будем
всегда изображать
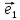
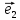
координат.
Определение
10. Координатами точки М на плоскости
относительно декартовой (аффинной)
системы координат {0;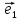
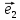
называют координаты ее радиус-вектора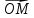
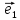
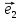
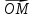
х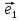
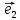
тогда числа х и у будет координатами М
относительно декартовой(аффинной)
системы координат {0;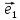
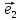
Координату х называютабсциссой точки
М, координату у-ординатой точки М.
Итак,
если выбрана система координат, {0;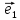
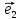
на плоскости, то каждой точке М плоскости
соответствует единственная точка М на
плоскости: эта точка является концом
вектора

х

Введение
системы координат лежит в основе метода
аналитической геометрии, сущность
которой состоит в том, чтобы уметь
сводить любую геометрическую задачу к
задачам арифметики или алгебры.
Определение
11. Координатами вектора
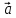
плоскости относительно декартовой
системы координат {0;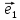
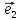
называют координаты этого вектора в
базисе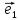
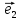
Чтобы
найти координаты вектора
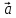
надо разложить его по базису

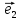
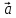
х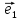
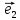
где коэффициенты х,у и будут координатами
вектора
относительно декартовой системы {0;

Декартова
(аффинная) система координат в пространстве.
Пусть
в пространстве зафиксирована некоторая
точка О(начало) и выбран векторный базис

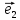
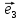
Определение
12. Совокупность {0;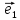
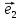
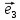
пространстве.
Определение
13. Три прямые проходящие через О и
параллельные соответственно векторам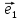
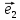
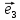
называютосями координат и обозначают
соответственно Оz,Oy,Oz.Мы
будем всегда изображать векторы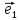
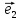
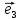
Определение
14. Координатами точки М в пространстве
относительно декартовой системы
координат {0;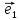
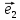
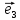
называют координаты ее радиус-вектора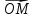
Иначе
говоря, координаты точки М – это такие
три числа х,у,zсоответственно
абсцисса и ордината точки М; третью
координатуzназывают
аппликатой точки М.
Введение
в пространстве декартовой системы
координат позволяет установить
взаимно-однозначное соответствие между
точками М пространства и упорядоченными
тройками чисел x,y,z.
Определение
15. Координатами вектора
в пространстве относительно декартовой
системы координат {0;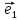
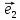
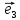
координаты этого вектора в базисе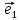
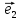
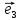
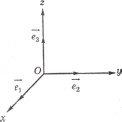
Пример
2.
Даны
три последовательные вершины
параллелограмма А(-2;1),В(1;3),С(4;0). Найти
четвертую его координату D.
Система координат аффинная.
Решение.
Векторы

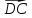
коэффициенты линейной комбинации):
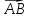
{3;2},


Значит,D(1;-2).
Ответ:D(1;-2).
Линейная
зависимость. Понятие базиса
Определение
16. Векторы
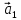

линейно зависимыми, если
существуют числа
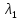
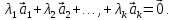
Это
определение линейной зависимости
векторов
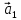
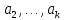
такому: векторы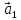
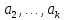
представить в виде линейной комбинации
остальных (или разложить по остальным).
Векторы
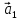
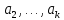
равенство (***) возможно в единственном
случае, когда
Понятие
линейной зависимости играет большую
роль в линейной алгебре. В векторной
алгебре линейная зависимость имеет
простой геометрический смысл.
-
Любые
два коллинеарных вектора линейно
зависимы, и наоборот, два неколлинеарных
вектора линейно независимы. -
Три
компланарных вектора линейно зависимы,
и наоборот, три некомпланарных вектора
линейно независимы. -
Каждые
четыре вектора линейно зависимы.
Определение
17. Три линейно
независимых вектора
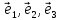
пространства, т.е.
любой вектор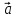
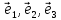
Определение
18. Два лежащих
в плоскости линейно независимых вектора
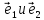
плоскости, т.е.
любой лежащий в этой плоскости вектор
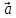
комбинации векторов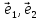
Задания
для самостоятельного решения.
-
Даны
три вектора
Найти
разложение векторапо
базису -
Даны
векторы
Вектор
–медиана
треугольникаOAB.
Разложить вектор
по
базису -
В
тетраэдре OABC
точки K,
L,
M,
N,
P,
Q
– середины рёбер OA,
OB,
OC,
AB,
AC,
BC
соответственно, S
– точка пересечения медиан треугольника
ABC.
Принимая за базисные
векторы
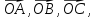
-
векторов
-
векторов
-
векторов
и
-
Точки
Mи
N
– середины сторон BCи
CDпараллелограмма
ABCD.
Разложить вектор
по
векторами
-
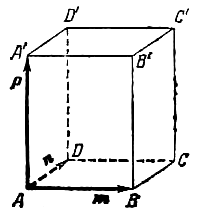
Дан
куб ABCDEFGH.
Разложить вектор
,
гдеK–
центр грани DHGC,
по векторам
,
-
На
плоскости даны вектора
Найти
разложение векторапо
базису,
-
На
плоскости даны три вектора
и
Определить разложение каждого из этих
трёх векторов, принимая в качестве
базиса два других. -
Принимая
в качестве базиса векторы
и
,
совпадающие со сторонами треугольникаABC,
определить разложение векторов,
приложенных в вершинах треугольника
и совпадающих с его медианами. -
Даны
четыре вектора
Найти координаты векторов – линейных
комбинаций: -
Даны
четыре вектора
,
Найти числа α, β, γ такие, что α
-
Проверить,
что векторы
образуют базис в пространстве. Найти
координаты векторов,
в
этом базисе. -
(Задача
об отрезке, разделённом в заданном
отношении.) Пусть точка C,
лежащая на отрезкеAB,
делит этот отрезок в отношении λ, т.е.
Выразить вектор
через векторы
и
-
Даны
две точки A(1;2;3).
B(7;2;5).
На прямой ABнайти
такую точку M,
чтобы точки Bи
Mбыли
расположены по разные стороны от точки
A и чтобы отрезок AMбыл
вдове длиннее отрезка AB.
Система координат аффинная. -
Вершина
Aпараллелепипеда
ABCD
принята за начало координат, а векторы
– за базисные векторы. Найти в этой
системе координаты всех вершин
параллелепипеда. -
Вершина
Oтетраэдра
OABCDпринята
за начало координат, а векторы
– за базисные векторы. Найти на этой
(аффинной) системе координаты точек
пересечения медиан граней тэтраэдра.
Жаль, что мы не можем делать здесь уравнения в стиле LaTeX (или может мы? Я не знаю, никогда не делал этого здесь…), но вот:
v1-v2 · v3-v4 = |v1-v2| * |v3-v4| * cos(a) (by definition)
определять |v3-v4| быть единичным вектором, так что
v1-v2 · v3-v4 = |v1-v2|*1*cos(a) = |v1-v2|*cos(a)
работа с левой стороны дает
v1·v4 + v2·v4 = |v1-v2|*cos(a) - v1·v3 + v2·v3
or
(v1+v2)·v4 = |v1-v2|*cos(a) - (v1-v2)·v3
в то время как
|v3-v4| = (v3-v4)·(v3-v4) = 1
Итак, есть 2 уравнения с 2 неизвестными. Теперь, для краткости,
aa = (v1+v2|x
bb = (v1+v2|y
x1 = v4|x
x2 = v4|y
A = |v1-v2|*cos(a) - (v1-v2)·v3
в котором |x означает x-компонента и т. д. При этом тривиальная замена дает нам
( (A-aa*x1)/bb )^2 + (aa*x1)^2 = 1 (-> 2 solutions)
( (A-bb*x2)/aa )^2 + (bb*x2)^2 = 1 (-> another 2 solutions)
Решения слишком запутаны, чтобы записывать их здесь, но они просты квадратные уравнения это можно легко решить.
Вы тогда имеете 4 уникальных вектора которые лежат на единичной окружности вокруг v3 (см. рисунок). Эти 4 вектора дают только 2 отдельные линии, но все равно неплохо найти все 4 вектора (в качестве самопроверки и для повышения надежности — могут быть некоторые крайние случаи, когда один из векторов таков, что что-то не так). нравится катастрофическая отмена происходит).
Какая линия лучше всего подходит для вас, зависит, конечно, от вашего варианта использования.
Какое бы решение вы ни выбрали, вы, конечно, всегда должны
arccos(((v1-v2)·(v3-v4))/|v1-v2|) = a
так, как это должно быть.





















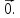
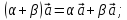
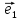
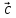
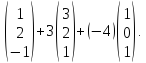




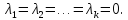
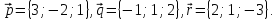 Найти
Найти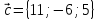 по
по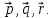
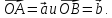 Вектор
Вектор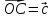 –медиана
–медиана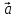 по
по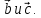

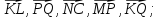
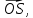 и
и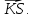
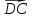 по
по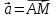 и
и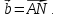
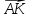 ,
,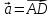 ,
,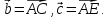
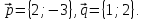 Найти
Найти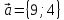 по
по ,
,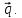
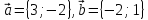 и
и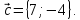 Определить разложение каждого из этих
Определить разложение каждого из этих и
и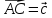 ,
,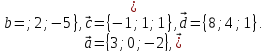 Найти координаты векторов – линейных
Найти координаты векторов – линейных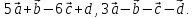
 ,
,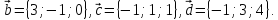 Найти числа α, β, γ такие, что α
Найти числа α, β, γ такие, что α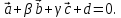
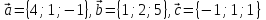 образуют базис в пространстве. Найти
образуют базис в пространстве. Найти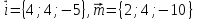 ,
,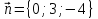 в
в Выразить вектор
Выразить вектор через векторы
через векторы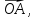 и
и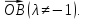

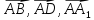
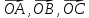 – за базисные векторы. Найти на этой
– за базисные векторы. Найти на этой
