Даны вершины треугольника как найти косинус - Сайт, где вы сможете решить свои вопросы

Мы уже находили косинусы углов треугольника по его сторонам в произвольном треугольнике и косинус острого угла прямоугольного треугольника.

Рассмотрим, как найти косинусы углов треугольника по его вершинам.

Задача

Дано: ΔABC,

A(-2;0), B(6;1), C(-3;-5).

1) Найти косинусы углов треугольника ABC;

2) Определить вид треугольника.

Решение:

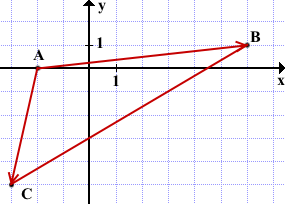1) Угол A образован векторами

(Чертёж не обязательно делать на координатной плоскости. Достаточно выполнить его схематически, для упрощения понимания, какой угол какими векторами образован).

Следовательно,

$[cos A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}}.]$

Найдём координаты векторов:

$[overrightarrow {AB} (x_B - x_A ;y_B - y_A ),]$

$[overrightarrow {AC} (x_C - x_A ;y_C - y_A ),]$

Находим скалярное произведение векторов:

Поскольку скалярное произведение меньше нуля, угол, образованный данными векторами, тупой. Значит треугольник ABC — тупоугольный.

Длины (или модули) векторов:

$[left| {overrightarrow {AB} } right| = sqrt {8^2 + 1^2 } = sqrt {65} ,]$

$[left| {overrightarrow {AC} } right| = sqrt {( - 1)^2 + ( - 5)^2 } = sqrt {26} .]$

Отсюда

$[cos A = frac{{ - 13}}{{sqrt {65} cdot sqrt {26} }} = frac{{ - 13}}{{sqrt {5 cdot 13 cdot 2 cdot 13} }} = ]$

$[= frac{{ - 13}}{{13sqrt {10} }} = - frac{1}{{sqrt {10} }} = - frac{{sqrt {10} }}{{10}}.]$

2) Угол B образован векторами

Таким образом,

$[cos B = frac{{overrightarrow {BA} cdot overrightarrow {BC} }}{{left| {overrightarrow {BA} } right| cdot left| {overrightarrow {BC} } right|}}.]$

Так как

— противоположные векторы, то их координаты отличаются только знаками и векторы имеют одинаковую длину:

$[overrightarrow {BC} (x_C - x_B ;y_C - y_B ),]$

$[left| {overrightarrow {BC} } right| = sqrt {( - 9)^2 + ( - 6)^2 } = sqrt {117} .]$

$[cos B = frac{{78}}{{sqrt {65} cdot sqrt {117} }} = frac{{13 cdot 6}}{{sqrt {5 cdot 13 cdot 9 cdot 13} }} =]$

$[= frac{{13 cdot 6}}{{13 cdot 3sqrt 5 }} = frac{2}{{sqrt 5 }} = frac{{2sqrt 5 }}{5}.]$

3) Угол C образован векторами

$[cos C = frac{{overrightarrow {CA} cdot overrightarrow {CB} }}{{left| {overrightarrow {CA} } right| cdot left| {overrightarrow {CB} } right|}}.]$

$[cos C = frac{{39}}{{sqrt {26} cdot sqrt {117} }} = frac{{13 cdot 3}}{{sqrt {2 cdot 13 cdot 9 cdot 13} }} = ]$

$[= frac{{13 cdot 3}}{{13 cdot 3sqrt 2 }} = frac{1}{{sqrt 2 }} = frac{{sqrt 2 }}{2}.]$

Ответ:

$[cos A = - frac{{sqrt {10} }}{{10}},cos B = frac{{2sqrt 5 }}{5},cos C = frac{{sqrt 2 }}{2};]$

ΔABC — тупоугольный.

Источник

Как найти косинус внутреннего угла при вершине В?

riuyt777
[0]

6 лет назад

Даны вершины треугольника А(2;-2;-2), В(2;2;-1) и С(3;1;-2).Найти косинус внутреннего угла при вершине В

Vasil Stryzhak
[11.5K]

6 лет назад

Вычислим стороны треугольника АВС, используя формулу определения расстояния между точками в прямоугольной декартовой системе координат в пространстве.

Затем, применив теорему косинусов, найдем искомый угол.

Решение:

а=ВС=√((3-2)²+(1-2)²+(-2+2)²)=√3

b=АС=√((3-2)²+(1+2)²+(-2+2)²)=√10

с=АВ=√((2-2)²+(2+2)²+(-1+2)²)=√17

cosβ=(a²+c²-b²)/2ac =(3+17-10)/(2√3*√17)=5/√51

Дополнительно: β=45⁰,56

система выбрала этот ответ лучшим

комментировать

в избранное

ссылка

отблагодарить

epimkin
[1.9K]

6 лет назад

Вот таким образом у меня получилось, если не ошибся в арифметике

комментировать

в избранное

ссылка

отблагодарить

SVFE48
[7.4K]

4 месяца назад

Чтобы найти косинус внутреннего угла при вершине В, нужно найти вектора, соединяющие вершину В с вершинами А и С. Вектор АВ будет иметь координаты (2-2; 2-(-2); (-1)-(-2))=(0;4;1). Вектор СВ будет иметь координаты (3-2; 1-2; (-2)-(-1))=(1;-1;-1). Теперь нужно найти скалярное произведение этих векторов и их длины. Скалярное произведение равно (01)+ (4-1) + (1*-1) = -5, а длины векторов равны sqrt(0^2+4^2+1^2)=sqrt(17) и sqrt(1^2+(-1)^2+(-1)^2)=sqrt(3). Таким образом, косинус внутреннего угла при вершине В равен -5/(sqrt(17)*sqrt(3))= -5/51= -0.09803921568627451.

комментировать

в избранное

ссылка

отблагодарить

storus
[73.8K]

5 лет назад

Найти косинус угла АВС можно по формуле для расчёта угла между двумя векторами.

Зная координаты вершин А(2;-2;-2), В(2;2;-1) и С(3;1;-2), находим вектора АВ = {0; -4; –1}, СВ = {1; -1; -1}. Для этого мы использовали формулу вида:

Затем полученные значения вставляем в следующую формулу:

Производим простые вычисления и получаем: cos a= 5/√51

комментировать

в избранное

ссылка

отблагодарить

Валерий Альбертович
[7K]

более года назад

Для начала вычислив вектор AB, вычтя из координат вершины B координаты вершины A. В итоге получаем AB = (0, 4, 1). Те же самые вычисления производим для вектора CB = (1, -1, -1). Далее подставляем в формулу cosa = (AB*CD)/(|AB|*|CD|) = 5/√51 – получили ответ.

комментировать

в избранное

ссылка

отблагодарить

Анна Сереевна Буянова
[0]

6 месяцев назад

Даны вершины треуольника АВС. Найти косинус угла при вершине А и площадь треугольника АВС

А(-3;-7;-5) В(0;-1;-2) С(-5;-6;-6). Напишите пожалуйста полное решение

комментировать

в избранное

ссылка

отблагодарить

Знаете ответ?

Источник

Как найти косинус угла треугольника с вершинами

Косинусом угла называется отношение прилежащего к данному углу катета к гипотенузе. Эта величина, как и другие тригонометрические соотношения, используется для решения не только прямоугольных треугольников, но и многих других задач.

Инструкция

Для произвольного треугольника с вершинами А, В и С задача нахождения косинуса одинакова для всех трех углов, если треугольник остроугольный. Если в треугольнике есть тупой угол, определение его косинуса следует рассмотреть отдельно.

В остроугольном треугольнике с вершинами А, В и С найдите косинус угла при вершине А. Опустите высоту из вершины В на сторону треугольника АС. Точку пересечения высоты со стороной АС обозначьте D и рассмотрите прямоугольный треугольник АВD. В этом треугольнике сторона АВ исходного треугольника является гипотенузой, а катеты — высота ВD исходного остроугольного треугольника и отрезок АD, принадлежащий стороне АС. Косинус угла А равен отношению АD/АВ, поскольку катет АD является прилежащим к углу А в прямоугольном треугольнике АВD. Если известно, в каком соотношении высота ВD делит сторону АС треугольника, то косинус угла А найден.

Если же величина АD не дана, но известна высота ВD, косинус угла можно определить через его синус. Синус угла А равен отношению высоты ВD исходного треугольника к стороне АС. Основное тригонометрическое тождество устанавливает связь между синусом и косинусом угла:

Sin² A+ Cos² A=1. Для нахождения косинуса угла А вычислите: 1- (ВD/AC)², из полученного результата нужно извлечь квадратный корень. Косинус угла А найден.

Если в треугольнике известны все стороны, то косинус любого угла найдите по теореме косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. Тогда косинус угла А в треугольнике со сторонами а, b, с вычислите по формуле: Cos A = (а²-b²-c²)/2*b*с.

Если в треугольнике нужно определить косинус тупого угла, воспользуйтесь формулой приведения. Тупой угол треугольника больше прямого, но меньше развернутого, он может быть записан как 180°-α, где α — острый угол, дополняющий тупой угол треугольника до развернутого. По формуле приведения найдите косинус: Cos (180°-α)= Cos α.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Подскажите, что надо делать для нахождения косинусов углов треугольника, если он задан координатами вершин?

Ученик

(100),
закрыт

12 лет назад

Matricfria

Мыслитель

(5124)

12 лет назад

А можно, чтобы найти угол А, сначала найти координаты векторов АВ и АС, а потом по формуле для косинуса угла между векторами:
косинус угла между векторами равен скалярному произведению векторов деленому на произведение модулей этих векторов.
cos a = b*c / IbI*IcI
Аналогично и косинусы других углов.

Вадим Терентьев

Просветленный

(23389)

12 лет назад

1)Находим уравнение прямых:
AB: (x-xa)/(xb-xa)=(y-ya)/(yb-ya)->(x-xa)/a1=(y-ya)/a2
Аналогично: BC: (x-xb)/b1=(y-yb)/b2; AC: (x-xc)/c1=(y-yc)/c2
2)Находим косинусы углов:
cosф=ab/[a], тогда:
cos(AB^BC)=(a1*b1+a2*b2)/(sqrt(a1^2+a2^2)*sqrt(b1^2+b2^2))
cos(BC^AC)=(b1*c1+b2*c2)/(sqrt(b1^2+b2^2)*sqrt(c1^2+c2^2))
cos(AC^AB)=(c1*a1+c2*a2)/(sqrt(c1^2_c2^2)*sqrt(a1^2+a2^2))

Источник

Как найти косинус угла треугольника с вершинами

Косинусом угла называется отношение прилежащего к данному углу катета к гипотенузе. Эта величина, как и другие тригонометрические соотношения,используется для решения не только прямоугольных треугольников, но и многих других задач.

Для произвольного треугольника с вершинами А, В и С задача нахождения косинуса одинакова для всех трех углов, если треугольник остроугольный. Если в треугольнике есть тупой угол, определение его косинусаследует рассмотреть отдельно.

В остроугольном треугольнике с вершинами А, В и С найдите косинус угла при вершине А. Опустите высоту из вершины В на сторонутреугольника АС. Точку пересечения высоты со стороной АС обозначьте D и рассмотрите прямоугольный треугольник АВD. В этом треугольнике сторона АВ исходного треугольника является гипотенузой, а катеты — высота ВD исходного остроугольного треугольника и отрезок АD, принадлежащий стороне АС. Косинус угла А равен отношению АD/АВ, поскольку катет АD является прилежащим к углу А в прямоугольном треугольнике АВD. Если известно, в каком соотношении высота ВD делит сторону АС треугольника, то косинус угла А найден.

Если же величина АD не дана, но известна высота ВD, косинус угла можно определить через его синус. Синус угла А равен отношению высоты ВD исходного треугольника к стороне АС.Основное тригонометрическое тождество устанавливает связь между синусом и косинусом угла:

Источник

Как найти косинус внутреннего угла при вершине В?

Как найти косинус угла треугольника с вершинами

Подскажите, что надо делать для нахождения косинусов углов треугольника, если он задан координатами вершин?

Как найти косинус угла треугольника с вершинами

Вам также может понравиться

Как правильно составить показания для суда

Как найти в слайм ранчер индигониум

Как составить урок на учи ру

Добавить комментарий Отменить ответ