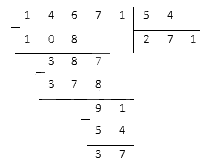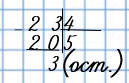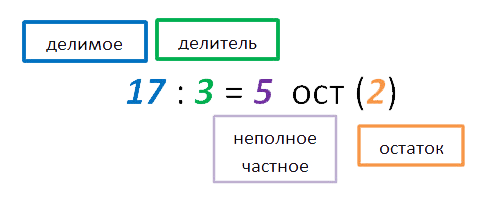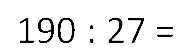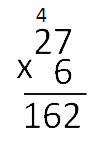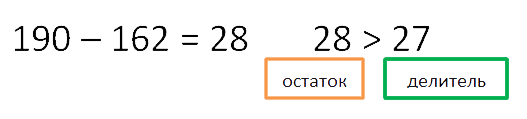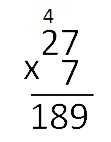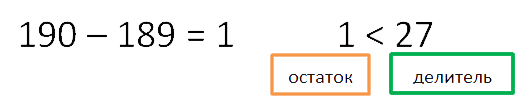Деление с остатком как найти неполное частное

Деление с остатком как найти неполное частное

Деление c остатком — арифметическая операция, играющая большую роль в арифметике, теории чисел, алгебре и криптографии. Чаще всего эта операция определяется для целых или натуральных чисел следующим образом[1]. Пусть a и b — целые числа, причём bneq 0. Деление с остатком a («делимого») на b («делитель») означает нахождение таких целых чисел q и r, что выполняется равенство:

a=bcdot q+r

Таким образом, результатами деления с остатком являются два целых числа: q называется неполным частным от деления, а r — остатком от деления. На остаток налагается дополнительное условие: {displaystyle 0leqslant r<|b|,} то есть остаток от деления должен быть неотрицательным числом и по абсолютной величине меньше делителя. Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел, то есть существует единственное решение уравнения a=bcdot q+r при заданных выше условиях. Если остаток равен нулю, говорят, что a нацело делится на b.

Нахождение неполного частного также называют целочисленным делением, а нахождение остатка от деления называют взятием остатка или, неформально, делением по модулю (однако последний термин стоит избегать, так как он может привести к путанице с делением в кольце или группе вычетов по аналогии со сложением или умножением по модулю).

Примеры
Проверка: 78=33cdot 2+12.
Проверка: -78=33cdot (-3)+21.
Проверка: {displaystyle -9=1cdot (-13)+4.}
Проверка: {displaystyle 9=90cdot 0+9.}

Операция деления с остатком может быть определена не только для целых чисел, но и для других математических объектов (например, для многочленов), см. ниже.

Определение[править | править код]

Оставаясь строго в рамках натуральных чисел, приходится различать деление с остатком и деление нацело, поскольку нулевой остаток не является натуральным числом; кроме того, неполное частное при делении меньшего числа на большее должно равняться нулю, что тоже выводит за рамки натуральных чисел. Все эти искусственные ограничения неоправданно усложняют формулировки, поэтому в источниках обычно либо рассматривается расширенный натуральный ряд, включающий ноль[2], либо теория сразу формулируется для целых чисел, как указано выше[1].

Для вычисления неполного частного от деления a на положительное число b следует разделить (в обычном смысле) a на b и округлить результат до ближайшего целого в меньшую сторону:

{displaystyle q=leftlfloor {frac {a}{b}}rightrfloor ,} когда b>0.

где полускобки {displaystyle leftlfloor cdot rightrfloor } обозначают взятие целой части. Значение неполного частного q позволяет вычислить значение остатка r по формуле:

{displaystyle r=a-bcdot q.}

Для отрицательного делителя нужно округлять частное в большую сторону:

{displaystyle q=leftlceil {frac {a}{b}}rightrceil ,} когда b<0.

Операция «mod» и связь со сравнениями[править | править код]


Величина остатка может быть получена бинарной операцией «взятия остатка» от деления a на b, обозначаемой mod:

{displaystyle r=a{bmod {b}}.}

Не следует путать это обозначение с обозначением сравнения по модулю b. Формула для r влечёт выполнение сравнения:

{displaystyle requiv a{pmod {b}},}

однако обратная импликация, вообще говоря, неверна. А именно, это сравнение не подразумевает выполнения неравенства 0leqslant r<|b|, необходимого для того, чтобы r было остатком.

В программировании[править | править код]

Операция вычисления неполного частного и остатка в различных языках программирования

Язык Неполное
частное		 Остаток Знак остатка
ActionScript % Делимое
Ada mod Делитель
rem Делимое
Бейсик MOD Не определено
Си (ISO 1990) / % Не определено
Си (ISO 1999) / % Делимое[3]
C++ (ISO 2003) / % Не определено[4]
C++ (ISO 2011) / % Делимое[5]
C# / % Делимое
ColdFusion MOD Делимое
Common Lisp mod Делитель
rem Делимое
D / % Делимое[6]
Delphi div mod Делимое
Eiffel // \ Делимое
Erlang div rem Делимое
Euphoria remainder Делимое
Microsoft Excel (англ.) QUOTIENT() MOD() Делитель
Microsoft Excel (рус.) ЧАСТНОЕ() ОСТАТ()
FileMaker Div() Mod() Делитель
Fortran mod Делимое
modulo Делитель
GML (Game Maker) div mod Делимое
Go / % Делимое
Haskell div mod Делитель
quot rem Делимое
J |~ Делитель
Java / % Делимое[7]
Math.floorDiv Math.floorMod Делитель (1.8+)
JavaScript .toFixed(0) % Делимое
Lua % Делитель
Mathematica Quotient Mod Делитель
MATLAB idivide(?, ?, 'floor') mod Делитель
idivide rem Делимое
MySQL DIV MOD
%		 Делимое
Oberon DIV MOD +
Objective Caml mod Не определено
Pascal div mod Делимое[8]
Perl Нет % Делитель
PHP Нет[9] % Делимое
PL/I mod Делитель (ANSI PL/I)
Prolog (ISO 1995) mod Делитель
PureBasic / Mod
%		 Делимое
Python // % Делитель
QBasic MOD Делимое
R %/% %% Делитель
RPG %REM Делимое
Ruby / % Делитель
Scheme modulo Делитель
SenseTalk modulo Делитель
rem Делимое
Tcl % Делитель
Verilog (2001) % Делимое
VHDL mod Делитель
rem Делимое
Visual Basic Mod Делимое

Нахождение остатка от деления часто используется в компьютерной технике и телекоммуникационном оборудовании для создания контрольных чисел и получения случайных чисел в ограниченном диапазоне, например в конгруэнтном генераторе случайных чисел.

Обозначения операции взятия остатка в различных языках программирования представлены в таблице справа.
Например, в Паскале операция mod вычисляет остаток от деления, а операция div осуществляет целочисленное деление, при котором остаток от деления отбрасывается: 

78 mod 33 = 12
78 div 33 = 2

Знак остатка[править | править код]

Операция взятия остатка в языках программирования может возвращать отрицательный результат (для отрицательного делимого или делителя). Тут есть два варианта:

  • Знак остатка совпадает со знаком делимого: неполное частное округляет к нулю.
  • Знак остатка совпадает со знаком делителя: неполное частное округляет к -infty .

Если в языке есть оба типа остатков, каждому из них соответствует своя операция неполного частного. Обе операции имеют жизненный смысл.

Операция div в x86/x64 делит регистровую пару rdx:rax на любой другой регистр или число из памяти[10]. Неполное частное и остаток выходят по первому варианту — округляют к нулю.

Как запрограммировать, если такой операции нет?[править | править код]

Неполное частное можно вычислить через деление и взятие целой части: q=left[{frac {a}{b}}right], где [x], в зависимости от задачи, может быть «полом» или усечением. Однако деление здесь получается дробное, которое намного медленнее целого. Такой алгоритм используется в языках, в которых нет целых типов (отдельные электронные таблицы, программируемые калькуляторы и математические программы), а также в скриптовых языках, в которых издержки интерпретации намного превышают издержки дробной арифметики (Perl, PHP).

При отсутствии команды mod остаток программируется как a-qb.

Если b положительно, а знак r совпадает со знаком делимого, не определён или неизвестен, для нахождения минимального неотрицательного остатка можно воспользоваться формулой r'=(b+(aoperatorname {mod}b))operatorname {mod}b.

Неполное частное и неотрицательный остаток от деления на степень двойки 2^{n} — это битовый сдвиг {displaystyle agg n} (для чисел со знаком — арифметический) и {displaystyle aoperatorname {&} (2^{n}-1)}.

Обобщения[править | править код]

Вещественные числа[править | править код]

Если два числа a и b (отличное от нуля) относятся к множеству вещественных чисел, a может быть поделено на b без остатка, и при этом частное также является вещественным числом. Если же частное по условию должно быть целым числом, в этом случае остаток будет вещественным числом, то есть может оказаться дробным.

Формально:

если a,bin {mathbb {R}},bneq 0, то {displaystyle a=bq+r}, где 0leqslant r<|b|.
Пример

Деление 7,9 на 2,1 с остатком даёт:

{displaystyle leftlfloor {frac {7{,}9}{2{,}1}}rightrfloor =3} (неполное частное);
{displaystyle 7{,}9-3cdot 2{,}1=1{,}6} (остаток).

Гауссовы целые числа[править | править код]

Гауссово число — это комплексное число вида a+bi, где a,b — целые числа. Для них можно определить деление с остатком: любое гауссово число u можно разделить с остатком на любое ненулевое гауссово число v, то есть представить в виде:

u=vq+r,

где частное q и остаток r — гауссовы числа, причём |r|<|v|.
Однако, в отличие от целых чисел, остаток от деления определяется неоднозначно. Например, {displaystyle 7+2i} можно разделить на {displaystyle 3-i} тремя способами:

{displaystyle 7+2i=(3-i)(2+i)+i=(3-i)(1+i)+3=(3-i)(2+2i)+(-1-2i).}

Многочлены[править | править код]

При делении с остатком двух многочленов f(x) и g(x) для однозначности результата вводится условие: степень многочлена-остатка должна быть строго меньше степени делителя:

{displaystyle f(x)=q(x)g(x)+r(x)}, причём {displaystyle deg(r)<deg(g)}.
Пример
{frac {2x^{2}+4x+5}{x+1}}=2x+2 (остаток 3), так как: {displaystyle 2x^{2}+4x+5=(x+1)(2x+2)+3}.

См. также[править | править код]

  • Алгоритм Евклида
  • Делимость
  • Наибольший общий делитель
  • Непрерывная дробь
  • Сравнение по модулю

Примечания[править | править код]

  1. ↑ 1 2 Деление // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2.
  2. ↑ Потапов М. К., Александров В. В., Пасиченко П. И. Алгебра и анализ элементарных функций. М.: Наука, 1981, 560 с., С. 9.
  3. ↑ ISO/IEC 9899:TC2: When integers are divided, the result of the / operator is the algebraic quotient with any fractional part discarded. [This is often called «truncation toward zero».]; в списке изменений 1999→TC1 и TC1→TC2 данное изменение не числится.
  4. ↑ «ISO/IEC 14882:2003 : Programming languages — C++», 5.6.4: International Organization for Standardization, International Electrotechnical Commission, 2003. «the binary % operator yields the remainder from the division of the first expression by the second. …. If both operands are nonnegative then the remainder is nonnegative; if not, the sign of the remainder is implementation-defined».
  5. ↑ N3242=11-0012 (Working draft), текст совпадает с C99
  6. ↑ D language specification (англ.). dlang.org. Дата обращения: 29 октября 2017. Архивировано из оригинала 3 октября 2017 года.
  7. ↑ Арнолд, Кен, Гослинг, Дж., Холмс, Д. Язык программирования Java. — 3-е изд. — М., СПб., Киев: Вильямс, 2001. — С. 173—174. — ISBN 5-8459-0215-0.
  8. ↑ Стандарт 1973 года: div — division with truncation.
  9. ↑ PHP: Arithmetic Operators — Manual. Дата обращения: 27 ноября 2014. Архивировано 19 ноября 2014 года.
  10. ↑ DIV — Unsigned Divide
Источник

Статья разбирает понятие деления целых чисел с остатком. Докажем теорему о делимости целых чисел с остатком и просмотрим связи между делимыми и делителями, неполными частными и остатками. Рассмотрим правила, когда производится деление целых чисел с остатками, рассмотрев подробно на примерах. В конце решения выполним проверку.

Общее представление о делении целых чисел с остатками

Деление целых чисел с остатком  рассматривается как обобщенное деление с остатком натуральных чисел. Это выполняется потому, что натуральные числа – это составная часть целых.

Деление с остатком произвольного числа говорит о том, что целое число a делится на число b, отличное от нуля. Если b=0, тогда не производят деление с остатком.

Также как и деление натуральных чисел с остатком, производится деление целых чисел a и b, при b отличном от нуля, на c и d. В этом случае a и b называют делимым и делителем, а d – остатком деления, с – целое число или неполное частное.

Если считать, что остаток – это целое неотрицательное число, тогда его величина не больше модуля числа b. Запишем таким образом: 0≤d≤b. Данная цепочка неравенств используется при сравнении 3 и более количества чисел.

Если с – неполное частное, тогда d – остаток от деления целого числа a на b, кратко можно зафиксировать: a:b=c (ост. d).

Остаток при делении чисел a на b возможен нулевой, тогда говорят, что a делится на b нацело, то есть без остатка. Деление без остатка считается частным случаем деления.

Если делим ноль на некоторое число, получаем в результате ноль. Остаток деления также будет равен нулю. Это можно проследить из теории о делении нуля на целое число.

Теперь рассмотрим смысл деления целых чисел с остатком.

Известно, что целые положительные числа – натуральные, тогда при делении с остатком получится такой же смысл, как и при  делении натуральных чисел с остатком.

При делении целого отрицательного числа а на целое положительное b имеется смысл. Рассмотрим на примере. Представив ситуацию, когда имеем долг предметов в количестве a, которое необходимо погасить b человек. Для этого необходимо каждому внести одинаковый вклад. Чтобы определить величину долга для каждого, необходимо обратить внимание на величину  частного с.  Остаток d говорит о том, что известно количество предметов после расплаты с долгами.

Рассмотрим на примере с яблоками. Если 2 человека должны 7 яблок. В случае, если посчитать, что каждый должен вернуть по 4 яблока, после полного расчета  у них останется 1 яблоко. Запишем в виде равенства это: (−7):2=−4 (ост. 1).

Деление любого числа а на целое не имеет смысла, но возможно как вариант.

Теорема о делимости целых чисел с остатком

Мы выявили, что а – это делимое, тогда b – это делитель, с – неполное частное, а d – остаток. Они между собой связаны. Эту связь покажем при помощи равенства a=b·c+d. Связь между ними характеризуется теоремой делимости с остатком.

Теорема

Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом: a=b·q+r, где q и r – это некоторые целые числа. Тут имеем 0≤r≤b.

Докажем возможность существования a=b·q+r.

Доказательство

Если существуют два числа a и b, причем a делится на b  без остатка, тогда  из определения следует, что имеется число q, что будет верно равенство a=b·q. Тогда равенство можно считать верным: a=b·q+r при r=0.

Если посчитать, что b – целое положительное число, тогда, следует выбрать целое q так, чтобы произведение b·q не было больше значения числа а, а произведение b·(q+1) было больше, чем a. 

Тогда необходимо взять q такое, чтобы данное неравенством b·q<a<b·(q+1) было верным. Необходимо вычесть b·q из всех частей выражения. Тогда придем к неравенству такого вида: 0<a−b·q<b.

Имеем, что значение выражения a−b·q больше нуля и не больше значения числа b, отсюда следует, что  r=a−b·q. Получим, что число а можем представить в виде a=b·q+r.

Теперь необходимо рассмотреть возможность представления a=b·q+r для отрицательных значений b.

Модуль числа получается положительным, тогда получим a=b·q1+r, где значение q1 – некоторое целое число, r – целое число, которое подходит условию 0≤r<b.  Принимаем q=−q1, получим, что a=b·q+r для отрицательных b.

Доказательство единственности

Допустим, что a=b·q+r, q и r являются целыми числами с верным условием 0≤r<b, имеется еще одна форма записи в виде a=b·q1+r1, где q1 и r1 являются некоторыми числами, где q1≠q , 0≤r1<b.

Когда из левой и правых частей вычитается неравенство, тогда получаем 0=b·(q−q1)+r−r1, которое равносильно r-r1=b·q1-q. Так как используется модуль, получим равенство r-r1=b·q1-q.

Заданное условие говорит о том, что 0≤r<b и 0≤r1<b запишется в виде r-r1<b. Имеем, что  q и q1 – целые, причем  q≠q1, тогда q1-q≥1. Отсюда имеем, что b·q1-q≥b. Полученные неравенства r-r1<b и b·q1-q≥b указывают на то, что такое равенство  в виде r-r1=b·q1-q невозможно в данном случае.

Отсюда следует, что по-другому число a быть представлено не может, кроме как такой записью a=b·q+r.

Связь между делимым, делителем, неполным частным и остатком

При помощи равенства a=b·c+d можно находить неизвестное делимое a, когда известен делитель b  с неполным частным c и остатком d.

Пример 1

Определить делимое, если при деление получим -21, неполное частное 5 и остаток 12.

Решение

Необходимо вычислить делимое a при известном делителе b=−21, неполным частным с=5 и остатком d=12. Нужно обратиться к равенству a=b·c+d, отсюда получим a=(−21)·5+12. При соблюдении порядка выполнения действий умножим -21 на 5, после этого получаем (−21)·5+12=−105+12=−93.

Ответ: -93.

Связь между делителем и неполным частным и остатком можно выразить при помощи равенств: b=(a−d):c, c=(a−d):b и  d=a−b·c. С их помощью мы можем вычислить делитель, неполное частное и остаток. Это сводится к постоянному нахождению остатка от деления целого целых чисел a на b с известным делимым, делителем и неполным частным. Применяется формула d=a−b·c. Рассмотрим решение подробно.

Пример 2

Найти остаток от деления целого числа -19 на целое 3 при известном неполном частном равном -7.

Решение

Чтобы вычислить остаток от деления, применим формулу вида d=a−b·c. По условию имеются все данные a=−19, b=3, c=−7.  Отсюда получим d=a−b·c=−19−3·(−7)=−19−(−21)=−19+21=2 (разность −19−(−21). Данный пример вычислен по правилу вычитания целого отрицательного числа.

Ответ: 2.

Деление с остатком целых положительных чисел, примеры

Все целые положительные числа являются натуральными. Отсюда следует, что деление выполняется по всем правилам деления  с остатком натуральных чисел. Скорость выполнения деления с остатком натуральных чисел важна, так как на нем основано не только деление положительных, но и правила деления целых произвольных.

Самый удобный метод деления – это столбик, так как проще и быстрее получить неполное или просто частное с остатком. Рассмотрим решение более подробно.

Пример 3

Произвести деление 14671 на 54.

Решение

Данное деление необходимо выполнять столбиком:

Деление с остатком целых положительных чисел, примеры

То есть неполное частное получается равным 271, а остаток – 37.

Ответ: 14 671:54=271. (ост. 37)

Правило деления с остатком целого положительного числа на целое отрицательное, примеры

Чтобы выполнить деление с остатком  положительного числа на целое отрицательное, необходимо сформулировать правило.

Определение 1

Неполное частное от деления целого положительного a на целое отрицательное b получаем число, которое противоположно неполному частному  от деления модулей чисел a на b. Тогда остаток  равен остатку при делении a на b.

Отсюда имеем, что неполное частное от деления целого полодительного числа на целое отрицательное число  считают целым неположительным числом.

Получим алгоритм:

  • найти модули делимого и делителя;
  • делить модуль делимого на модуль делителя, тогда получим неполное частное  и
  • остаток;
  • запишем число противоположное полученному.

Рассмотрим на примере алгоритма деления целого положительного числа на целое отрицательное.

Пример 4

Выполнить деление с остатком 17 на  -5.

Решение

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное. Необходимо разделить 17 на -5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2.

Получим, что искомое число от деления 17 на -5 =-3 с остатком равным 2.

Ответ: 17:(−5)=−3 (ост. 2).

Пример 5

Необходимо разделить 45 на -15.

Решение

Необходимо разделить числа по модулю. Число 45 делим на 15, получим частное 3 без остатка. Значит, число 45 делится на 15 без остатка. В ответе получаем -3, так как деление производилось по модулю.

45:(-15)=45:-15=-45:15=-3

Ответ: 45:(−15)=−3.

Деление с остатком целого отрицательного числа на целое положительное, примеры

Формулировка правила деления с остатком выглядит следующим образом.

Определение 2

Для того, чтобы получить неполное частное с при делении целого отрицательного  a на положительное b, нужно применить противоположное данному числу и вычесть из него 1, тогда остаток d будет вычисляться по формуле: d=a−b·c.

Исходя из правила можно сделать вывод, что при делении получим целое неотрицательное число. Для точности решения применяют алгоритм деления а на b с остатком:

  • найти модули делимого и делителя;
  • делить по модулю;
  • записать противоположное данному число и вычесть 1;
  • использовать формулу для остатка d=a−b·c.

Рассмотрим на примере решения, где применяется данный алгоритм.

Пример 6

Найти неполное частное и остаток от деления -17 на 5.

Решение

Делим заданные числа по модулю. Получаем, что при делении частное равно 3, а остаток 2. Так как получили 3, противоположное -3. Необходимо отнять 1.

−3−1=−4.

Искомое значение полчаем равное -4.

Чтобы вычислить остаток, необходимо a=−17, b=5, c=−4, тогда d=a−b·c=−17−5·(−4)=−17−(−20)=−17+20=3.

Значит, неполным частным от деления является число -4 с остатком равным 3.

Ответ: (−17):5=−4 (ост. 3).

Пример 7

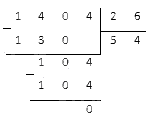
Разделить целое отрицательное число -1404 на положительное 26.

Решение

Необходимо произвести деление столбиком и по мудулю.

Деление с остатком целого отрицательного числа на целое положительное, примеры

Мы получили деление модулей чисел без остатка. Это значит, что деление выполняется без остатка, а искомое частное =-54.

Ответ: (−1 404):26=−54.

Правило деления с остатком целых отрицательных чисел, примеры

Необходимо сформулировать правило деления с остатком целых отрицательных чисел.

Определение 3

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, необходимо произвести вычисления по модулю, после чего прибавить 1, тогда сможем произвести вычисления по формуле d=a−b·c.

Отсюда следует, что неполное частное от деления целых отрицательных чисел будет число положительное.

Сформулируем данное правило в виде алгоритма:

  • найти модули делимого и делителя;
  • разделить модуль делимого на модуль делителя  с получением неполного частного с
  • остатком;
  • прибавление 1 к неполному частному;
  • вычисление остатка, исходя из формулы d=a−b·c.

Данный алгоритм рассмотрим на примере.

Пример 8

Найти неполное частное и остаток при делении -17 на -5.

Решение

Для правильности решения применим алгоритм для деления с остатком. Для начала раздели числа по модулю. Отсюда получим, что неполное частное =3, а остаток равен 2. По правилу необходимо сложить неполное частное и 1. Получим, что 3+1=4. Отсюда получим, что неполное частное от деления заданных чисел равно 4.

Для вычисления остатка мы применим формулу. По условию имеем, что a=−17, b=−5, c=4, тогда, используя формулу, получим d=a−b·c=−17−(−5)·4=−17−(−20)=−17+20=3. Искомый ответ, то есть остаток, равен 3, а неполное частное равно 4.

Ответ: (−17):(−5)=4 (ост. 3).

Проверка результата деления целых чисел с остатком

После выполнение деления чисел с остатком необходимо выполнять проверку. Данная проверка подразумевает 2 этапа. Вначале идет проверка остатка d на неотрицательность, выполнение условия 0≤d<b. При их выполнении разрешено выполнять 2 этап. Если 1 этап  не выполнился, значит вычисления произведены с ошибками. Второй этап состоит из того, что равенство a=b·c+d должно быть верным. Иначе в вычисления имеется ошибка.

Рассмотрим на примерах.

Пример 9

Произведено деление -521 на -12. Частное равно 44, остаток 7. Выполнить проверку.

Решение

Так как остаток – это число положительное, то его величина является меньше, чем модуль делителя. Делитель равен -12, значит, его модуль равен 12. Можно переходить к следующему пункту проверки.

По условию имеем, что a=−521, b=−12, c=44, d=7. Отсюда вычислим b·c+d, где b·c+d=−12·44+7=−528+7=−521. Отсюда следует, что равенство верное. Проверка пройдена.

Пример 10

Выполнить проверку деления (−17):5=−3 (ост. −2). Верно ли равенство?

Решение

Смысл первого этапа заключается в том, что необходимо проверить деление целых чисел с остатком. Отсюда видно, что действие произведено неверно, так как дан остаток, равный -2. Остаток не является отрицательным числом.

Имеем, что второе условие выполненное, но недостаточное для данного случая.

Ответ: нет.

Пример 11

Число -19 разделили на -3. Неполное частное равно 7, а остаток 1. Проверить, верно ли выполнено данное вычисление.

Решение

Дан остаток, равный 1. Он положительный. По величине меньше модуля делителя, значит, первый этап выполняется. Перейдем ко второму этапу.

Вычислим значение выражения b·c+d. По условию имеем, что b=−3, c=7, d=1, значит, подставив числовые значения, получим b·c+d=−3·7+1=−21+1=−20.  Следует, что a=b·c+d равенство не выполняется, так как в условии дано а=-19.

Отсюда следует вывод, что деление произведено с ошибкой.

Ответ: нет.

Источник
  1. Главная
  2. Справочники
  3. Справочник по математике для начальной школы
  4. Деление
  5. Деление с остатком

Начнём рассмотрение новой темы с решения задачи.

Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?

8 : 2 = 4 (к.)

Каждый ребёнок получил по 4 конфеты.

На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?

Каждый получил по 2 конфеты и 2 конфеты остались лишними.

Как это записать?

8 : 3 = 2 (ост. 2)

Как сделать проверку?

2 • 3 + 2 = 8

Правило 1

Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.

16 : 7 = 2 (ост. 2)

23 : 8 = 2 (ост. 7)

Правило 2

При делении с остатком остаток всегда должен быть меньше делителя.

43 : 8 = 5 (ост. 3)

остаток 3 < делимого 5

34 : 4 = 8 (ост. 2)

остаток 2 < делимого 4

Правило 3

Если делимое меньше делителя, в частном получается ноль, а остаток равен делимому.

7 : 10 = 0 (ост. 7)

6 : 9 = 0 (ост. 6)

Порядок решения

14 : 5 = 2 (ост. 4)

1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.

10 : 5 = 2

2. Вычитаю из делимого найденное число: 14 − 10 = 4

3. Сравниваю остаток с делителем

4 < 5

Решение верно.

Проверка деления с остатком

1. Умножаю неполное частное на делитель.

2. Прибавляю остаток к полученному результату.

3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.

Деление в столбик

В 23 содержится 5 раз по 4, и ещё остаётся 3.

Решение записывают так:

23 : 4 = 5 (ост. 3) или так:

, где 23 – делимое, 4 – делитель, 5 – неполное частное, а 3  – остаток.

Советуем посмотреть:

Табличное деление

Внетабличное деление

Деление суммы на число

Деление на однозначное число

Деление чисел, оканчивающихся нулями

Свойства деления

Деление


Правило встречается в следующих упражнениях:

2 класс

Страница 76. Урок 29,
Петерсон, Учебник, часть 3

Страница 77. Урок 29,
Петерсон, Учебник, часть 3

Страница 79. Урок 30,
Петерсон, Учебник, часть 3

Страница 80. Урок 30,
Петерсон, Учебник, часть 3

Страница 81. Урок 31,
Петерсон, Учебник, часть 3

Страница 82. Урок 31,
Петерсон, Учебник, часть 3

Страница 84. Урок 32,
Петерсон, Учебник, часть 3

Страница 87. Урок 33,
Петерсон, Учебник, часть 3

Страница 108. Повторение,
Петерсон, Учебник, часть 3

3 класс

Страница 56. ПР. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 61. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 40,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 58,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 71. Урок 24,
Петерсон, Учебник, часть 1

Страница 87. Урок 32,
Петерсон, Учебник, часть 1

Страница 17. Урок 7,
Петерсон, Учебник, часть 3

4 класс

Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 38,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 47,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 10. ПР 3. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 63,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 67,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

5 класс

Задание 529,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 550,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1082,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1724,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 532,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

Задание 8,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

Задание 6,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

Задание 1,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2

Номер 860,
Мерзляк, Полонский, Якир, Учебник

Номер 1222,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 497,
Мерзляк, Полонский, Якир, Учебник

Номер 499,
Мерзляк, Полонский, Якир, Учебник

Номер 1159,
Мерзляк, Полонский, Якир, Учебник

Номер 6,
Мерзляк, Полонский, Якир, Учебник

Задание 604,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 638,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1134,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1158,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1364,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 8,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

7 класс

Номер 209,
Мерзляк, Полонский, Якир, Учебник

Номер 330,
Мерзляк, Полонский, Якир, Учебник

Номер 351,
Мерзляк, Полонский, Якир, Учебник

Номер 385,
Мерзляк, Полонский, Якир, Учебник

Номер 574,
Мерзляк, Полонский, Якир, Учебник

Номер 582,
Мерзляк, Полонский, Якир, Учебник

Номер 583,
Мерзляк, Полонский, Якир, Учебник

Номер 602,
Мерзляк, Полонский, Якир, Учебник

Номер 606,
Мерзляк, Полонский, Якир, Учебник

Номер 1045,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 46,
Мерзляк, Полонский, Якир, Учебник

Номер 47,
Мерзляк, Полонский, Якир, Учебник

Номер 141,
Мерзляк, Полонский, Якир, Учебник

Номер 193,
Мерзляк, Полонский, Якир, Учебник

Номер 207,
Мерзляк, Полонский, Якир, Учебник

Номер 241,
Мерзляк, Полонский, Якир, Учебник

Номер 254,
Мерзляк, Полонский, Якир, Учебник

Номер 304,
Мерзляк, Полонский, Якир, Учебник

Номер 305,
Мерзляк, Полонский, Якир, Учебник

Номер 307,
Мерзляк, Полонский, Якир, Учебник

Источник

Деление с остатком.

Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.

Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?

Решение:
Поделим число 16 на 5 столбиком получим:

Деление с остатком
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.

16=5⋅3+1

a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.

Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.

Остаток от деления

Остаток всегда должен быть меньше делителя.

Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.

Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.

Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.

Остаток может быть равен делителю?
Ответ: нет.

Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)

Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8

Решение:
а) Делим столбиком:
Деленис с остатком 258:7

258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6<7.

Подставим в формулу и проверим правильно ли мы решили пример:
7⋅36+6=252+6=258

б) Делим столбиком:
Деление с остатком 1873:8

1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1<8.

Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873

Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?

Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.

Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?

Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.

Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)

Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22

б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107

Задача:

Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?

Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400

Ответ: 30 кусков получиться и 10 см. проволоки останется.

Источник

Не всегда можно полностью разделить одно число на другое. В примерах на деление может
оставаться остаток. Такое деление называется деление с остатком.

Запомните!
!

Деление с остатком — это деление одного натурального числа на другое, при котором
остаток не равен нулю.

Если при делении натуральных чисел остаток равен нулю, то говорят, что делимое
делится на делитель без остатка, или, иначе говоря, делится нацело.

Деление с остатком записывают так:

деление с остатком

Читается пример следующим образом:

«17» разделить на
«3» получится «5» и остаток «2».

Порядок решения примеров на деление с остатком.

  1. Находим наибольшее число до «17»,
    которое делится на «3» без остатка. Это «15».

    15 : 3 = 5

  2. Вычитаем из делимого найденное число из пункта «1».

    17 − 15 = 2

  3. Сравниваем остаток с делителем.
    сравниваем остаток с делителем

Запомните!
!

При делении с остатком остаток всегда должен быть меньше делителя.

Если получилось, что остаток больше делителя, значит, вы неверно нашли
наибольшее число, которое делится на делитель без остатка.

  1. Записываем ответ.

    17 : 3 = 5 ост (2)

При решении более сложных примеров не всегда можно легко найти наибольшее число из пункта 1.
Иногда для этого необходимо произвести дополнительные расчёты в столбик. Покажем это на примере.

деление с остатком пример

Методом подбора найдём на сколько надо умножить «27»,
чтобы получить ближайшее число к «190».

Попробуем умножить на «6».

расчёт в столбик

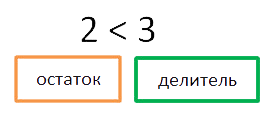
Рассчитаем остаток и сравним его с делителем.

рассчитаем остаток

Остаток больше делителя. Это означает, что «6» как множитель нам не подходит. Попробуем
умножить делитель на «7».

расчёт в столбик

Снова рассчитаем и сравним остаток с делителем.

сравниваем остаток

Остаток меньше делителя. Значит пример решён верно. Запишем ответ.

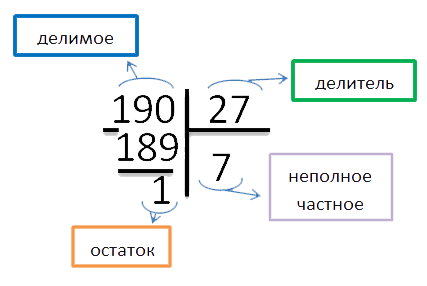
190 : 27 = 7 ост (1)

Все вычисления выше можно представить в виде деления в столбик. Правила деления в столбик вы можете
освежить в уроке «Деление в столбик» на
нашем сайте.

деление с остатком в стобик

Как проверить деление с остатком

  1. Умножить неполное частное на делитель
  2. Прибавить к полученному результату остаток
  3. Сравнить полученный результат с делимым

Проверим ответ нашего примера.

190 : 27 = 7 ост (1)

  1. 27 · 7 = 189
  2. 189 + 1 = 190
  3. 190 = 190

Деление с остатком выполнено верно.

Запомните!
!

Если при делении с остатком делимое меньше делителя, то их неполное частное равно нулю,
остаток равен делимому.

Например:

  • 6 : 10 = 0 ост (6)
  • 14 : 112 = 0 ост (14)
  • 31 : 45 = 0 ост (31)

Другими словами, если вы делите меньшее число на большее, неполное частное всегда будет равно нулю.

Ваши комментарии

Важно!
Галка

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Пришелец пожимает плечами

Оставить комментарий:

21 октября 2019 в 18:04

Мария Левицкая
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Мария Левицкая
Профиль
Благодарили: 0

Сообщений: 1

76: 12 = a (ост.4)
Как решить уравнение с остатком и при этом с  неизвестным неполным числом??? 

0
Спасибоthanks
Ответить

13 ноября 2019 в 6:48
Ответ для Мария Левицкая

Валя Гутник
(^-^)
Профиль
Благодарили: 0

Сообщений: 7

(^-^)
Валя Гутник
Профиль
Благодарили: 0

Сообщений: 7


Χ − −  

             много кратные числа и решить это невозможно          
 

♥ 

0
Спасибоthanks
Ответить

24 января 2017 в 19:31

Нуралы Оразов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Нуралы Оразов
Профиль
Благодарили: 0

Сообщений: 1

:32 = 7(30 ост)

0
Спасибоthanks
Ответить

11 февраля 2017 в 14:14
Ответ для Нуралы Оразов

Алексей Карапов
(^-^)
Профиль
Благодарили: 0

Сообщений: 9

(^-^)
Алексей Карапов
Профиль
Благодарили: 0

Сообщений: 9


Если я правильно понял вопрос то решение:
(7 · 32) +30 = 224+30=254
                                                     7 · 32 =7 · 30+7 · 2 =210+14=224;
Делаем проверку (если конечно надо):
254 :32=7(30 ост);

0
Спасибоthanks
Ответить

14 марта 2016 в 16:11

Евгения Болошова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Евгения Болошова
Профиль
Благодарили: 0

Сообщений: 1

51: 7=

0
Спасибоthanks
Ответить

14 марта 2016 в 16:28
Ответ для Евгения Болошова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


 = 7 

0
Спасибоthanks
Ответить

18 февраля 2016 в 22:44

Олеся Клименкова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Олеся Клименкова
Профиль
Благодарили: 0

Сообщений: 1

(9x+2z)всё во второй степени -(8x+3z)(4x-4z)

0
Спасибоthanks
Ответить

20 февраля 2016 в 16:41
Ответ для Олеся Клименкова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


Равно то чему? Хотябы задачу озвучивайте, если лень решать.

0
Спасибоthanks
Ответить

20 февраля 2016 в 17:04
Ответ для Олеся Клименкова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


(9x+2z)2 — (8x+3z)(4x-4Z)=
(9x)2 + 2*9x*2z + (2z)2-(8x*4x-8x*4z+3z*4x-3z*4z)=
81x2+36xz+4z2-32x2+32xz-12xz+12z2=
49x2+56xz+16z2

0
Спасибоthanks
Ответить

16 февраля 2016 в 18:44

Наталья Шипова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Наталья Шипова
Профиль
Благодарили: 0

Сообщений: 1

0
Спасибоthanks
Ответить

20 февраля 2016 в 13:23
Ответ для Наталья Шипова

Кристина Кот
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Кристина Кот
Профиль
Благодарили: 0

Сообщений: 1


6: 1000=0,006

0
Спасибоthanks
Ответить

4 марта 2016 в 16:23
Ответ для Наталья Шипова

Лиза Котик
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Лиза Котик
Профиль
Благодарили: 0

Сообщений: 2


0 (ост 006)sealed 

0
Спасибоthanks
Ответить

11 февраля 2016 в 15:43

Алена Ершова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Алена Ершова
Профиль
Благодарили: 0

Сообщений: 1

сколько получится 29 разделить на 3 с остаткомfrown напишите пж

0
Спасибоthanks
Ответить

11 февраля 2016 в 17:00
Ответ для Алена Ершова

Сулейманова Телихан
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Сулейманова Телихан
Профиль
Благодарили: 0

Сообщений: 2


будет 27(ост.2)innocent

0
Спасибоthanks
Ответить

11 февраля 2016 в 17:01
Ответ для Алена Ершова

Сулейманова Телихан
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Сулейманова Телихан
Профиль
Благодарили: 0

Сообщений: 2


если тебе надо дробь то 27  

0
Спасибоthanks
Ответить

19 сентября 2016 в 11:57
Ответ для Алена Ершова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


9 (ост. 2)

0
Спасибоthanks
Ответить

14 декабря 2016 в 16:41
Ответ для Алена Ершова

Наташа Сафонова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Наташа Сафонова
Профиль
Благодарили: 0

Сообщений: 1


9?

0
Спасибоthanks
Ответить

1 февраля 2016 в 17:07

Даня Вишняков
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Даня Вишняков
Профиль
Благодарили: 0

Сообщений: 1

(10100+90900)/100/5*4+101*2 помогите

0
Спасибоthanks
Ответить

3 февраля 2016 в 20:17
Ответ для Даня Вишняков

Сергей Аколоцев
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Сергей Аколоцев
Профиль
Благодарили: 0

Сообщений: 3


10100+90900=101000
101000/100=1010
1010/5=202
202*4=808
101*2=202
808+202=1010

0
Спасибоthanks
Ответить

23 января 2016 в 13:29

Александра Сирота
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Александра Сирота
Профиль
Благодарили: 0

Сообщений: 2

ПОМОГИТЕ ПОЖАЛУЙСТА    5.6:3.2= у меня получается 1.24 но это не правельно должно быть 1.75 я не пойму почему 

0
Спасибоthanks
Ответить

24 января 2016 в 10:54
Ответ для Александра Сирота

Владимир Талаев
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Владимир Талаев
Профиль
Благодарили: 0

Сообщений: 1


у тебя не получается, потому что надо перенести запятую на одно чило вправо в обоих числах

0
Спасибоthanks
Ответить

24 января 2016 в 13:40
Ответ для Александра Сирота

Инна Шабрашина
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Инна Шабрашина
Профиль
Благодарили: 0

Сообщений: 5


56/32= 1.75
-32
___
240
-224
____
160
-160
____
0
                       

0
Спасибоthanks
Ответить

21 января 2016 в 17:46

Дарина Жиенбаева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Дарина Жиенбаева
Профиль
Благодарили: 0

Сообщений: 1

436680:17=
204261:26=
269093:43=
23045:54=

0
Спасибоthanks
Ответить

22 января 2016 в 13:29
Ответ для Дарина Жиенбаева

Валерия Харламова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Валерия Харламова
Профиль
Благодарили: 0

Сообщений: 1


436680:17=25687(ост.1)
204261:26=7856(ост.5)
269093:43=6257(ост.42)
23045:54=426(ост.41)

0
Спасибоthanks
Ответить

30 ноября 2015 в 22:29

Vladimir Bobkov
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Vladimir Bobkov
Профиль
Благодарили: 0

Сообщений: 1

Найдите неполное частоное и остаток при делении:
243 на 15 
как это понять помогите пожалуйста)

0
Спасибоthanks
Ответить

9 декабря 2015 в 19:47
Ответ для Vladimir Bobkov

Тима Клюев
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Тима Клюев
Профиль
Благодарили: 0

Сообщений: 8


делимое — делитель = неполноя частное (ост. x)

0
Спасибоthanks
Ответить

16 сентября 2016 в 14:35
Ответ для Vladimir Bobkov

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


Думаю эта статья вам поможет. Там подробно рассмотрен данный вопрос.

0
Спасибоthanks
Ответить

4 октября 2015 в 17:34

Анастасия Белоусова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Анастасия Белоусова
Профиль
Благодарили: 0

Сообщений: 1

84:9=? 50:12=?

0
Спасибоthanks
Ответить

4 октября 2015 в 20:18
Ответ для Анастасия Белоусова

Ильяна Петрова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Ильяна Петрова
Профиль
Благодарили: 0

Сообщений: 1


9 и остаток 3.2)4 и остаток 2

0
Спасибоthanks
Ответить

29 октября 2015 в 16:04
Ответ для Анастасия Белоусова

Марья Голдобина
(^-^)
Профиль
Благодарили: 0

Сообщений: 4

(^-^)
Марья Голдобина
Профиль
Благодарили: 0

Сообщений: 4


84 : 9=9 (остаток 3)

50 : 12=5
(способом подбора)

0
Спасибоthanks
Ответить

26 сентября 2015 в 19:56

Николай Фадеев
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Николай Фадеев
Профиль
Благодарили: 0

Сообщений: 1

один токарь  работал 5 ч и сделал 45 деталей второй работал  с той же производительностью и сделал 90 деталей. Найдите время работы второго токаря

0
Спасибоthanks
Ответить

12 сентября 2016 в 13:26
Ответ для Николай Фадеев

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


Производительность, это количество деталей произведенное за единицу времени. Для нахождение производительности необходимо количество деталей раздлеить на время изготовления.
45: 5 = 9. 9 деталей в час — производительность токарей.
Найдём время работы второго токаря.
90: 9 = 10 часов. Работал второй токарь.
Ответ: 10 часов.

0
Спасибоthanks
Ответить

26 сентября 2015 в 13:19

Мария Логачёва
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Мария Логачёва
Профиль
Благодарили: 0

Сообщений: 1

за 3 дня Рокфор съел 230 головок сыра за первый день он съел 74 головки, что на 16 головок больше, чем за второй. Сколько головок сыра съел Рокфор за третий день?

0
Спасибоthanks
Ответить

12 сентября 2016 в 13:38
Ответ для Мария Логачёва

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197


Найдём сколько головок сыра Рокфор съел за второй день. Известно, что в первый день он съел на 16 головок больше, чем во второй. Значит во второй день он съел 74 ? 16 = 58. Головок Сыра съел Ракфор во второй день. Чтобы найти количество головок сыра, съеденного ракфором в третий день, нужно из общего количества головок вычести сыр, съеденный в первый и второй дни.
230 ?74 ?58 = 98.
Проверка: 74+58+98 = 230.
Ответ: 98 головок съел Рокфор за третий день.

0
Спасибоthanks
Ответить

5 июля 2015 в 14:56

Дмитрий Сергеев
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Дмитрий Сергеев
Профиль
Благодарили: 0

Сообщений: 1

Приветствую. Предстоит тестирование на поступление в вуз. Калькулятор брать запрещенно. Как можно быстро вычислить это выражение? Ведь делить в столбик такие числа не быстро а на задание дается всего лишь 3 мин.25*77/145

0
Спасибоthanks
Ответить

9 июня 2016 в 14:46
Ответ для Дмитрий Сергеев

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60


  = 72.

0
Спасибоthanks
Ответить

5 июля 2015 в 1:05

Полина Иванова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Полина Иванова
Профиль
Благодарили: 0

Сообщений: 1

коробка с 60 конфетами весит 2 кг, а без конфет 200г. какая масса одной конфеты если все они одинаковыsmile

0
Спасибоthanks
Ответить

26 июля 2015 в 17:50
Ответ для Полина Иванова

Лина Макарова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Лина Макарова
Профиль
Благодарили: 0

Сообщений: 1


2 кг=2000г1)2000-200=1800г2)1800:60=30г масса одной конфетыПроверка:30 · 60=1800г1800 + 200=2000г=2кгОтвет:30 гcool

0
Спасибоthanks
Ответить

Источник

Добавить комментарий