ldsilishare849
Вопрос по физике:
Что такое дельта в физике, объясните пожалуйста самым обычным способом а то я в интернете нашел но нечего не понял? заранее спасибо
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 2
yelrmprdepu
Дельта в физике означает приращение какой-либо величины. То есть разность СТАЛО минус БЫЛО (обычно речь идет о приращении величины за какой-то промежуток времени)
Пример. Скорость была v₁ = 4м/с а немного погодя стала v₂ = 6м/с. Тогда
Δv = v₂ – v₁ = 2м/с
ereala513
Дельта – ∆ – это разность того, что получилось и того, чтобы было первоначально, т.е. изменение чего-либо
Например ∆t = t2 – t1 – дельта Т показывает, насколько изменилась температура
∆l = l2 – l1 – дельта l показывает, насколько изменилась длина (или, например, настолько растянулась пружина, если решать задачу, где указана жесткость пружины), и т д
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
Содержание:
При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.
Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.
При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.
Пример:
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).
Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)
Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.
Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.
Относительная погрешность измерения ε (ЭПСИЛОН)
Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим:  . То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
. То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):
 (5.1)
(5.1)
Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.
Стандартная запись результата измерений и выводы
Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0  0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.
На точность измерения влияет много факторов, в частности:
- При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
- Не вполне ровно установили рулетку.
- Наша рулетка является копией эталона и может несколько отличаться от оригинала.
Все это необходимо учитывать при проведении измерений.
Итоги:
- Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
- Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора.
- Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:
 и указывает на качество измерения. Ее можно выразить в процентах.
и указывает на качество измерения. Ее можно выразить в процентах.
Измерительные приборы
Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.
Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.
Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.
Как определяют единицы длины и времени
В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.
Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).
Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.
Можно ли расстояние измерять годами
Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!
Что надо знать об измерительных приборах
Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?
Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.
Как определить цену деления шкалы? Для этого необходимо:
- выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
- подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
- вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
- Для линейки 1:
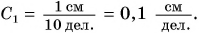
- Для линейки 2:
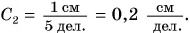
- Для линейки 3:
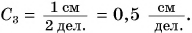
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:


А какими линейкой и мензуркой можно измерить точнее?
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы
Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы  ), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления
), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления  ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.
). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.
Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.
Главные выводы:
- Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
- Цена деления шкалы равна значению наименьшего деления шкалы.
- Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.
Для любознательных:
В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.
- Заказать решение задач по физике
Пример решения задачи
Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:
1) Цена деления нижней шкалы:

Цена деления средней шкалы:

Цена деления верхней шкалы:
2) Определенный но нижней шкале с точностью до 10°  определенный по средней шкале с точностью до 5°
определенный по средней шкале с точностью до 5°  определенный по верхней шкале с точностью до 1°
определенный по верхней шкале с точностью до 1° 
- Определение площади и объема
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Как зарождалась физика
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
В физике и некоторых других науках греческой буквой D («дельта») принято обозначать разницу между определенными параметрами. Это могут быть, например, температура, время, давление, длины отрезков, расстояния между координатами по одной и той же оси и т.д. Латинской буквой t чаше всего обозначают время и температуру.

Вам понадобится
- – данные измерений;
- – калькулятор.
Инструкция
Если буквой t в данном разделе физики обозначается температура, проведите измерения температуры. Термометр может быть любым. Нужно, чтобы его шкала соответствовала нужной вам степени точности. Разумеется, измерять оба показателя необходимо по одному и тому же термометру.
Второй показатель зависит от условий задачи. Например, если вам нужно отследить изменение состояния объекта, снимите второй показатель через некоторое время. Самый доступный эксперимент – измерить температуру своего тела утром и вечером. Вычтите из большего числа меньшее. Это и будет дельта t. Поскольку температура с течением времени может как увеличиваться, так и уменьшаться, вам нужен модуль разности.
В задаче может быть предложено и сравнение изменений разных объектов. Дельта t в этом случае приобретает несколько иной смысл, но все равно она остается разностью температур. Например, вам нужно определить, насколько нужно разогреть горелку, чтобы расплавить два разных металла. Сравните температуры плавления одного и другого вещества. Точно так же, как и в первом случае, вычтите из большего показателя меньший. Если вы проводите эксперимент, то сначала вам нужно разогреть горелку до меньшей температуры, затем прибавить к ней Dt, что и даст вам температуру плавления другого металла.
Во многих отраслях знаний буквой t обозначают время. Выражение «дельта t» в этих случаях также означает разность, но уже в показаниях часов. Засеките время и запишите результат. Подождите немного и снова посмотрите на часы. Допустим, в первый раз вы посмотрели на циферблат ровно в 14 часов, а второй — по прошествии 13 минут. Разность в этом случае составляет 13 минут. Это и есть Dt по условиям данной задачи.
На практике довольно часто приходится определять Dt без всяких вычислений. Например, во время соревнований по легкой атлетике арбитру важно знать, за какое время бегуны пробежали ту или иную дистанцию. При этом не особенно важно, во сколько начались состязания, объявлен старт раньше или позже указанного в афишах времени. В этом случае судья определяет только Dt. В начале забега он ставит секундомер на 0, а в конце – отмечает результат.
Обратите внимание
Определить Dt бывает необходимо и при сравнении движения разных объектов при прочих равных условиях. Этот способ тоже наиболее понятен, если представить себе спортсменов. Допустим, участников соревнований очень много, они все бегут одну и ту же дистанцию, но в разных забегах. Судьям нужно понять, кто окажется на каком месте в итоговой таблице. Для этого определяется лучший результат – в данном случае минимальный. С ним сравниваются все остальные. То есть каждый раз судьи находят Dt между временем первого и второго, второго и третьего спортсменов и т.д.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Путь и перемещение, теория и онлайн калькуляторы
Путь и перемещение
При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь
Определение
Путь – длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь – это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
[Delta s=left|x_2-x_1right|left(1right),]
где $x_1$ – координата начального положения тела; $x_2$ – конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
[Delta s=vt left(2right),]
где $t$ – время движения тела.
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
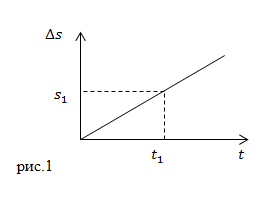
Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку ${Delta s}_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Определение
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
[Delta overline{r}=overline{r }left(t+Delta tright)-overline{r }left(tright)left(3right).]
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки – это перемещение ($Delta overline{r}$).
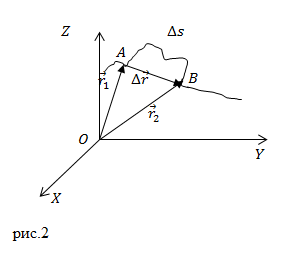
В декартовой системе координат радиус-вектор точки представляют в виде:
[overline{r }left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(4right),]
где $overline{i}$, $overline{j}$,$ overline{k}$ – единичные орты осей X,Y,Z. Тогда $Delta overline{r}$ равен:
[Delta overline{r}=left[xleft(t+Delta tright)-xleft(tright)right]overline{i}+left[yleft(t+?tright)-yleft(tright)right]overline{j}+left[zleft(t+?tright)-zleft(tright)right]overline{k}left(5right).]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
[left|Delta overline{r}right|=Delta s left(6right).]
Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overline{r}right|$ или просто $Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
[Delta overline{r}=Delta {overline{r}}_1+Delta {overline{r}}_2+dots left(7right).]
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Пример 1
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
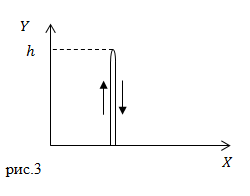
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь – длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
[Delta s=2h.]
Перемещение – направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
[Delta r=0.]
Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$
Пример 2
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
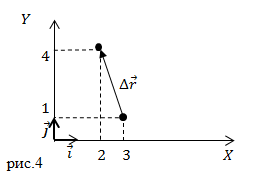
Радиус – вектор начальной точки запишем как:
[{overline{r }}_0left(tright)=x_0left(tright)overline{i}+y_0left(tright)overline{j}=3overline{i}+1overline{j}left(2.1right).]
Радиус – вектор конечной точки имеет вид:
[overline{r}left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}=2overline{i}+4overline{j}left(2.2right).]
Вектор перемещения представим как:
[Delta overline{r}=left[xleft(tright)-x_0left(tright)right]overline{i}+left[уleft(tright)-у_0left(tright)right]overline{j}=left[2-3right]+left[1-4right]overline{j}=-1overline{i}+3overline{j}(2.3).]
Из формулы видим, что:
[Delta r_x=-1;;Delta r_y=3. ]
Ответ: $Delta r_x=-1;;Delta r_y=3 $
Читать дальше: равнодействующая всех сил.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Обновлено: 15.05.2023
Физика. Наука, изучающая явления природы, свойства и строение материи.
Материя . Всё, что есть во Вселенной.
Молекула . Мельчайшая частица данного вещества.
Диффузия . Взаимное перемешивание молекул одного вещества с молекулами другого.
Механическое движение . Изменение положения тела относительно других тел с течением времени.
Путь . Длина траектории.
Траектория . Линия, по которой движется тело.
Равномерное движение. Движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.
Скорость . Величина, равная отношению пути ко времени, за которое этот путь пройден.
Инерция . Явление сохранения скорости тела при отсутствии действия на него других тел.
Тормозной путь . Путь, который проходит автомобиль после выключения двигателя до полной остановки.
Плотность . Физическая величина, равная отношению массы тела к его объёму.
Сила. Мера механического воздействия на тело со стороны других тел.
Масса. Мера инертности.
Вес. Сила, с которой тело вследствие притяжения к Земле действует на горизонтальную опору или подвес.
Равнодействующая сила . Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Сила трения . Сила, возникающая при движении одного тела по поверхности другого и направленная против движения.
Давление . Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности.
Атмосфера . Воздушная оболочка Земли.
Архимедова сила . Сила, выталкивающая тело из жидкости или газа.
Работа. Величина, равная произведению приложенной силы на пройденный путь.
Мощность. Величина, равная отношению работы ко времени, за которое она была совершена.
Рычаг. Твёрдое тело, которое может вращаться вокруг неподвижной опоры.
КПД. Отношение полезной работы к полной работе.
Потенциальная энергия . Энергия взаимодействия.
Кинетическая энергия . Энергия движения.
Определения и формулы
Измерение физических величин
Измерение физических величин
- из значения верхней границы (ВГ) шкалы вычесть значение нижней границы (НГ) шкалы и результат разделить на количество делений (N);
- найти разницу между значениями двух соседних числовых меток (А и Б) шкалы и разделить на количество делений между ними (n).
ЦД = (ВГ — НГ) / N
ЦД = (Б — А) / n
Механическое движение
Скорость (ʋ) — физическая величина, численно равна пути (S), пройденного телом за единицу времени (t).
Путь (S) — длина траектории, по которой двигалось тело, численно равен произведению скорости (ʋ) тела на время (t) движения.
Время движения (t) — равно отношению пути (S), пройденного телом, к скорости (ʋ) движения.
Средняя скорость (ʋ ср ) — равна отношению суммы участков пути (S1, S2, S3, …), пройденного телом, к промежутку времени (t1 + t2+ t3+ …), за который этот путь пройден.
ʋср = (S1 + S2 + S3 + …) / (t1 + t2 + t3 + …)
Сила тяжести, вес, масса, плотность
Сила тяжести — сила (FТ), с которой Земля притягивает к себе тело, равная произведению массы (т) тела на коэффициент пропорциональности (g) — постоянную величину для Земли. (g = 9,8 H/кг)
FТ = m*g
Вес (Р) — сила, с которой тело действует на горизонтальную опору или вертикальный подвес, равная произведению массы (т) тела на коэффициент (g).
Масса (т) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (Р) к коэффициенту (g).
т = Р / g
Плотность (ρ) — масса единицы объёма вещества, численно равная отношению массы (т) вещества к его объёму (V).
Механический рычаг, момент силы
Момент силы (М) равен произведению силы (F) на сё плечо (l)
М = F*l
Условие равновесия рычага — рычаг находится в равновесии, если плечи (l1, l2)действующих на него двух сил (F1, F2) обратно пропорциональны значениям сил.
a) F1 / F2 = l1 / l2
Давление, сила давления
Давление (р) — величина, численно равная отношению силы (F), действующей перпендикулярно поверхности, к площади (S) этой поверхности
Сила давления (F) — сила, действующая перпендикулярно поверхности тела, равная произведению давления (р) на площадь этой поверхности (S)
Давление газов и жидкостей
Давление однородной жидкости (р) — на дно сосуда зависит только от её плотности (ρ) и высоты столба жидкости (h).
Закон Архимеда — на тело, погруженное в жидкость (или газ), действует выталкивающая сила — архимедова сила (FВ). равная весу жидкости (или газа), в объёме (VТ) этого тела.
FВ = ρ*g*Vт
Условие плавания тел — если архимедова сила (FВ) больше силы тяжести (FТ)тела, то тело всплывает.
FВ > FТ
Закон гидравлической машины — силы (F1, F2), действующие на уравновешенные поршни гидравлической машины, пропорциональны площадям (S1, S2) этих поршней.
F1 / F2 = S1 / S2
Закон сообщающихся сосудов — однородная жидкость в сообщающихся сосудах находится на одном уровне (h)
Работа, энергия, мощность
Механическая работа — Работа (A) — величина, равная произведению перемещения тела (S) на силу (F), под действием которой это перемещение произошло.
Формула:
А = F*S
Коэффициент полезного действия механизма (КПД) — коэффициент полезного действия (КПД) механизма — число, показывающее, какую часть от всей выполненной работы (АВ) составляет полезная работа (АП).
ɳ = АП / АВ *100%
Потенциальная энергия (Е П ) тела, поднятого над Землей, пропорциональна его массе (т) и высоте (h) над Землей.
Формула:
ЕП = m*g*h
Кинетическая энергия (Е К ) движущегося тела пропорциональна его массе (m) и квадрату скорости (ʋ 2 ).
ЕК = m*ʋ 2 / 2
Сохранение и превращение механической энергии — Сумма потенциальной (ЕП) и кинетической (ЕК) энергии в любой момент времени остается постоянной.
EП + EК = const
Мощность (N) — величина, показывающая скорость выполнения работы и равная:
а) отношению работы (А) ко времени (t), за которое она выполнена;
б) произведению силы (F), под действием которой перемещается тело, на среднюю скорость (ʋ) его перемещения.
Формулы меры длины и веса и соотношения между единицами

12 самых востребованных формул по физике в 7 классе
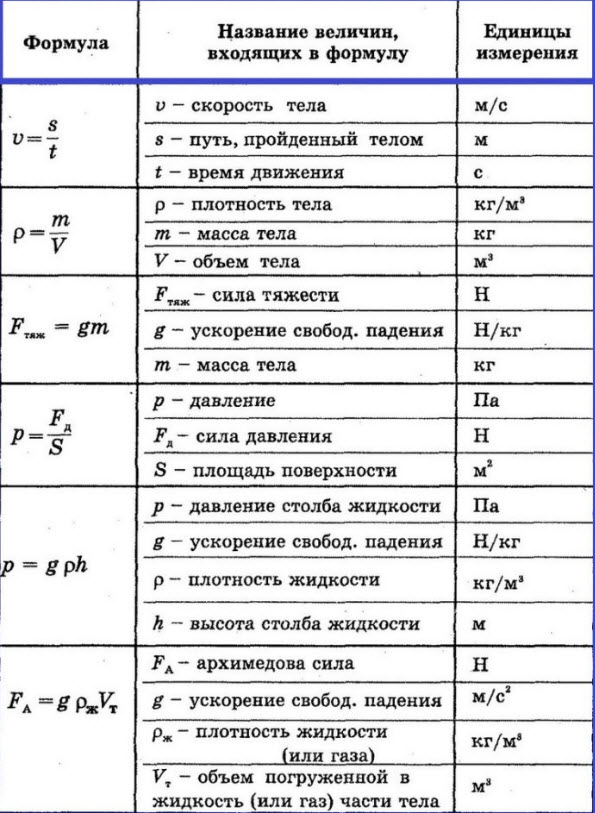

Тест для закрепления материала
- Сколько в теле молекул
- Чему равна масса тела из данного вещества
- Что массы разных тел неодинаковы
- Отношение массы тела к его объему
2 Вычислите скорость (в м/с) равномерного полёта воздушного шара в течение 1,5 мин., за которые он пролетел 540 м
Дельта-функция применяется в математической физике при решении задач, в которые входят сосредоточенные величины.
ДЕЛЬТА-ФУНКЦИЯ, d-функция Дирака, символ, применяемый в математической физике при решении задач, в которые входят сосредоточенные величины (нагрузка, заряд и т. п.) . Дельта-функция — простейшая обобщенная функция; она характеризует, напр. , плотность распределения масс, при котором в одной точке сосредоточена единичная масса, а любой интервал, не содержащий этой точки, свободен от масс.
разность напр. сила пружины= Г=к*дельтаХ
(г- вместо ф латинского, дельтаХ- величина растяжения пружины)

Физика
Понятия и определения

Физика — наука, изучающая явления природы, свойства и строение материи.
Материя — все то, что реально существует во Вселенной, независимо от нашего сознания.
Молекула — наименьшая частица вещества, определяющая его свойства и способная к самостоятельному существованию.
Диффузия — взаимное перемешивание молекул одного вещества с молекулами другого.
Механическое движение — изменение положения тела относительно других тел с течением времени.
Путь — длина траектории.
Траектория — линия, по которой движется тело.
Равномерное движение — движение, при котором тело за любые равные промежутки времени проходит одинаковые пути.
Скорость — величина, равная отношению пути ко времени, за которое этот путь пройден.
Инерция — явление сохранения скорости тела при отсутствии действия на него других тел.
Тормозной путь — путь, который проходит автомобиль после выключения двигателя до полной остановки.
Плотность — физическая величина, равная отношению массы тела к его объёму.
Сила — мера механического воздействия на тело со стороны других тел.
Масса — мера инертности.
Вес — сила, с которой тело вследствие притяжения к Земле действует на горизонтальную опору или подвес.
Равнодействующая сил — сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Сила трения — сила, возникающая при движении одного тела по поверхности другого и направленная против движения.
Давление — величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности.
Атмосфера — воздушная оболочка Земли.
Архимедова сила — сила, выталкивающая тело из жидкости или газа.
Работа — величина, равная произведению приложенной силы на пройденный путь.
Мощность — величина, равная отношению работы ко времени, за которое она была совершена.
Рычаг — твёрдое тело, которое может вращаться вокруг неподвижной опоры.
В данной статье поговорим о знаке Дельта – что он из себя представляет, в каких сферах применяется и для чего вообще используется. Также вы узнаете, как выглядит знак и как его можно вставить в текст в такой программе, какой является Ворд из Майкрософт Оффис.
Знак Дельта применяется во многих сферах жизнедеятельности, к примеру, в физике, текстовых редакторах, формулах и других сферах. Чаще всего именно при печати учебной литературы, докладов и других видов документов применяют знак дельта, который имеется в разных версиях ВОРД от Виндовс и других приложениях для создания документов текстового формата на ПК.

О происхождения знака
Буква, которая служит аналогом в русском алфавите – Д, а вот символ везде одинаков и изображается, как геометрическая фигура, а именно треугольник с равными сторонами (Δ). Эта версия является заглавной, прописная версия выглядит немного иначе, представляя собой кружок с хвостиком, похожий на обозначение в физике плотности (δ).

Где применяется данный символ?
Кроме использования в правописании греков, символ начали активно применять в математике, геометрии, алгебре, физике, химии и географии.
Поговорим отдельно о применении дельта в каждых научных сферах:
- География. Дельта подразумевает в географическом смысле начальную часть реки, океана или моря, имеет смысловое, нежели символическое, буквенное понятие и восприятие. Почему именно область впадения реки принято так называть? Все просто, дело в форме данной области, если сделать снимок сверху, то отток реки будет иметь форму правильного треугольника, а символ дельта, как раз представляет собой такой геометрический объект. Ярчайшим представителем с выраженной дельтой является река Нил (Египет), которая впадает в Средиземное море, а также Амазонка с ее впадением в океан Атлантики.
- Применение в математике, алгебре, геометрии. Очень часто знак применяют в математической сфере для таких целей, как: 1) Приращение аргумента подразумевает под дельтой измененную переменную. К примеру, сложим 5 и 4 в итоге получим число 9. Дельтой будет являться увеличение 5 на 4. 2) Применение в теории вероятности по системе Лапласа. Такой метод преподают в ВУЗах, а не школах и в нем используют такой знак. 3) А также символ применяется при обозначении прямой и обратной матриц. 4) Дельта, буква, применяемая в написании формул (как письменным методом, так и через компьютер);
- Также в математике применяют прописную версию дельта. А именно, такой символ обозначает производную от числа. Обозначение выглядит следующим образом – δy/δx. 2) Используется для описания бесконечной функции-дельта. Бесконечная функция возможна, если все значения аргумента равны нулю. 3) При помощи δ еще обозначают символику Кронекера, символ равен всегда 1, при условии того, что все его индексы равны, либо нулевые при заданных условиях.
- Физика, астрономия, космогония. Граничащие меж собой научные дисциплины, все особо важные и по-своему интересные, в каждой из дисциплин можно встретить знак дельта. В физике связь всех производных осуществляется при помощи формул с интеграцией. К примеру, формула скорости, которая выглядит следующим образом – δS к δt , является отношением одной части к другой. В данном случае расстояние, которое преодолел объект, соотносится со временем, затраченном на преодоление. Вторая производная – это ускорение, где тоже важна взаимосвязь одной составляющей формулы к другой. В космологии и астрономии применяют формулы, расчеты с данным символом, только в прописном варианте.

Поставь лайк, это важно для наших авторов, подпишись на наш канал в Яндекс.Дзен и вступай в группу Вконтакте
Читайте также:
- История названия каспийского моря кратко
- История адама и евы в исламе кратко
- Освобождение анголы и мозамбика кратко
- Конституционная реформа 2005 года в великобритании кратко
- Эдуард лимонов биография кратко
