Путь и перемещение, теория и онлайн калькуляторы
Путь и перемещение
При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь
Определение
Путь – длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь – это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
[Delta s=left|x_2-x_1right|left(1right),]
где $x_1$ – координата начального положения тела; $x_2$ – конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
[Delta s=vt left(2right),]
где $t$ – время движения тела.
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
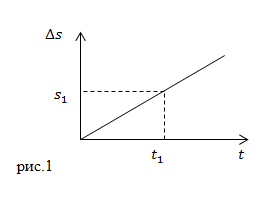
Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку ${Delta s}_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Определение
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
[Delta overline{r}=overline{r }left(t+Delta tright)-overline{r }left(tright)left(3right).]
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки – это перемещение ($Delta overline{r}$).
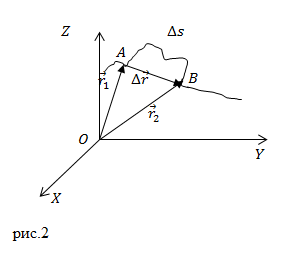
В декартовой системе координат радиус-вектор точки представляют в виде:
[overline{r }left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(4right),]
где $overline{i}$, $overline{j}$,$ overline{k}$ – единичные орты осей X,Y,Z. Тогда $Delta overline{r}$ равен:
[Delta overline{r}=left[xleft(t+Delta tright)-xleft(tright)right]overline{i}+left[yleft(t+?tright)-yleft(tright)right]overline{j}+left[zleft(t+?tright)-zleft(tright)right]overline{k}left(5right).]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
[left|Delta overline{r}right|=Delta s left(6right).]
Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overline{r}right|$ или просто $Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
[Delta overline{r}=Delta {overline{r}}_1+Delta {overline{r}}_2+dots left(7right).]
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Пример 1
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
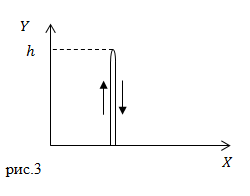
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь – длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
[Delta s=2h.]
Перемещение – направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
[Delta r=0.]
Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$
Пример 2
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
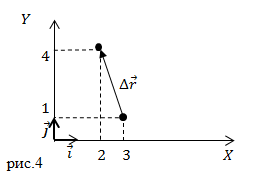
Радиус – вектор начальной точки запишем как:
[{overline{r }}_0left(tright)=x_0left(tright)overline{i}+y_0left(tright)overline{j}=3overline{i}+1overline{j}left(2.1right).]
Радиус – вектор конечной точки имеет вид:
[overline{r}left(tright)=xleft(tright)overline{i}+yleft(tright)overline{j}=2overline{i}+4overline{j}left(2.2right).]
Вектор перемещения представим как:
[Delta overline{r}=left[xleft(tright)-x_0left(tright)right]overline{i}+left[уleft(tright)-у_0left(tright)right]overline{j}=left[2-3right]+left[1-4right]overline{j}=-1overline{i}+3overline{j}(2.3).]
Из формулы видим, что:
[Delta r_x=-1;;Delta r_y=3. ]
Ответ: $Delta r_x=-1;;Delta r_y=3 $
Читать дальше: равнодействующая всех сил.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Содержание материала
- Кинематика
- Видео
- Как выглядит формула пути без времени, когда скорость тела уменьшается
- Импульс
- График скорости равномерного движения
- Виды движения и формулы длины пути
- Основные формулы электричества
- Примеры решения задач
Кинематика
К оглавлению…
Путь при равномерном движении:

Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):

Средняя скорость пути:

Средняя скорость перемещения:

Определение ускорения при равноускоренном движении:

Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:

Средняя скорость при равноускоренном движении:

Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:



Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):



Формула для тормозного пути тела:

Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:

Дальность полета тела при горизонтальном броске с высоты H:

Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:


Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):


Определение периода вращения при равномерном движении по окружности:

Определение частоты вращения при равномерном движении по окружности:

Связь периода и частоты:

Линейная скорость при равномерном движении по окружности может быть найдена по формулам:

Угловая скорость вращения при равномерном движении по окружности:

Связь линейной и скорости и угловой скорости выражается формулой:

Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):

Центростремительное ускорение находится по одной из формул:

Видео
Как выглядит формула пути без времени, когда скорость тела уменьшается
Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:
[large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]
Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:
[ large begin{cases} S = v_{0} cdot t — displaystyle frac{a}{2} cdot t^{2} \ v = v_{0} — a cdot t end{cases} ]
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:

Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):

Общий импульс системы тел (важно то, что сумма векторная):

Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:

Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

График скорости равномерного движения
Т.к. скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.

Если динозавр начнет двигаться к дому, то его скорость будет положительной, т.к. направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, т.к. направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.

Из графика видно, что скорость с течением времени не изменяется – она постоянна в любой выбранный момент времени. Из графика положительной скорости мы видим, что $upsilon = 6 frac{м}{с}$; из графика отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 с$.
$$S = upsilon t = 6 frac{м}{с} cdot 4 c = 24 м$.$
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути $Delta s$ на отрезке времени от $t$ до $t + Delta t$ находят как:
где $langle vrangle$ – средняя путевая скорость. При равномерном движении $langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
где a – постоянное ускорение, v – начальная скорость движения.
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:

Переходим к постоянному электрическому току:

Далее добавляем формулы по теме: “Магнитное поле электрического тока”

Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:

Ну и, конечно, куда же без электромагнитных колебаний:

Примеры решения задач
1. Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 м}{3600 с} approx 33 frac{м}{с}$.
Дано:$upsilon=120 frac{км}{ч}$$t = 3 c$СИ:$upsilon=33 frac{м}{с}$
Найти:$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t = 33 frac{м}{с} cdot 3 с approx 100 м$
Ответ: $100 м$
2. Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$;
$900 км = 900 000 м$.
Дано:$upsilon_{ср} = 40 frac{км}{ч}$$S = 900 км$CИ:$upsilon_{ср} = 11 frac{м}{с}$$S = 900 000 м$
Найти:$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}} = frac{900 000 м}{11 frac{м}{с}} approx 82 000 с$.
Переведем время в часы:
$1 ч = 60 мин = 60 cdot 60 c = 3600 c$.
Тогда,
$t = frac{82 000 c}{3600 c} approx 23 ч$.
Ответ: $t = 82 000 c = 23 ч$.
Теги
Для описания
движения выбирают тело отсчета – это
произвольны выбор тела относительно
которых определяется положение других
движущихся тел.
Система
координат
– это система связанная с телом отсчета
(в противном случае декартовая система
координата)
Система
отсчета –
это совокупность тел отсчета связанная
с ним системой координат и синхронизированных
между сомой часов.
Положение точки А
характеризуется 3 координатами
При движении
материальной точки координаты будут
изменяться
Уравнение
движения материальной точки
x=x(f)
y=y(f)
z=z(f)
r=r(f)
6.Скорость (средняя. Ее модуль, мгновенная скорость и ее модуль). Путь, траектория, вектор перемещения, длинна пути.
Траектория
– это линия
отсчитываемая движущиеся материальной
точкой то есть выбор системы координат.
Траектория в разл.
системе отсчета может быть разная если
траектория деления
прямая линия
–прямолинейной
Кривая линия –
криволинейной
Если тело находится
в точке А потом перемещается в точку В
то
дельтаr=r0-r
Это приращения
вектора r
за промежуток времени дельта ф
Длинна пути
дельта s(t)
– это пройденный промежуток времени
s
– скалярный вектор
Если все точки
траектории лежат в одной плоскости то
движение называется плоским
Скорость
– векторная
величина определяющая как быстроту
движения так и его направление в данный
момент времени.
Средняя
скорость
– векторная величина определяемая
дельта r
вращения к прошедшему времени вращения.
<v>=дельта
r/дельта
t
Направление вектора
средней
скорости
<v>=|<v>|=дельта
r/дельта
t
= |дельта r/дельта
t|=
дельта s/дельта
t
Мгновенная
скорость
v
– это векторная величина определяемая
первой производной r
вектора движущейся точки ко времени
v=lim
дельта r/дельта
t
(при t
стрем. к 0)= дельта r/дельта
t
Векторные скорости
направлены по касательной к т.А
Модуль
мгновенной скорости
v
v=|v|=|lim
дельта r/дельта
t
(при t
стрем. к 0)|= дельта s/дельта
t
Длинна
пути s
пройденного за промежуток точкой есть
s=интеграл
от t2
до t1
от v(t)dt
(м/с)
7. Ускорение и его составляющее (среднее, мгновенное, нормальное, тангинцеальное, полное ускорение при криволинейном движении)
Ускорение
– есть
характеристика ее равномерного движения
и определяет быстроту
изменения скорости
как по модулю или по направлению.
Существует понятие движение по окружности
с ускорением.
Среднее
ускорение
– это векторная величина равная отношению
изменения скорости к интервалу времени
<a>=
дельта v/дельта
t
Мгновенное
ускорение
а векторная величина определяемое
первой производной скорости ко времени
a=
lim
дельта v/дельта
t
(при t
стрем. к 0)|= дельта v/дельта
t
Составляющее
ускорение может быть
а).Тангенциальным
– характеризует
быстроту изменения скорости по модулю.
Она направлена по касательной к траектории
а тангенциальное
дельта v/дельта
t
б).Нормальное
составляющее
характеризует изменение скорости по
величине и направлению, характеризует
быстроту изменения скорости по
направленности. Она направлена к центру
изменения траектории.
а нормальное дельта
v
в квадрате/дельта r
Тангенциальное
ускорение – постоянная величина .
Нормальное ускорение
=0 появляется при движении по окружности.
Криволинейное
равнопеременное движение
Полное ускорение
при криволинейном геометрическом
движении
нормальное+тангенциальное
движение
а (м/с2)
8.Угловая скорость,
период вращения, углы поворота, частота,
скорость. Вращательное
движение твердого тела – движение при
котором все точки движущейся по окружности
центры которых лежат на одной прямой
называемой осью вращения.
Существует угловая
скорость
векторная величина определяемая
следующим образом.
w=lim
дельта f/дельта
t
(при t
стрем. к 0)|= дельта f/дельта
t
Пер. угла поворота
ко времени
где df
– вектор
Элементы угла
поворота df
рассчитываются как вектора
Модуль вектора df
равен углу
поворота,
а что направление совпадает с направлением
поступательного движения острия винта
головка которого вращается в в направлении
движения точки по окружности что
подчиняется правилу правого винта (если
точка движется по окружности против
часовой стрелки).
Поэтому угловая
скорость будет направлена по оси движения
Еденица w=1
рад/с
Период
вращения
время за которое точка совершает полный
оборот
w=2пи/Т
где Т-период
Линейная
скорость
точка движущейся по окружности
Линейная скорость
v=lim
дельта s/дельта
t
(при t
стрем. к 0)=lim
R*дельта
f/дельта
t
(при d
стрем. к 0)
v=Rw
Частота
вращения
– это число полных оборотов совершаемых
телом в единицу времени
Число полных
оборотов совершаемом за единицу времени
назывеется частотой вращения
n=1/T=w/2пи
w=2пи*n
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Движение Равномерное и Прямолинейное
2006-10-20 23:44
Движение Равномерное и Прямолинейное
Для описания этого случая достаточно знать функциональную
зависимость одной из трех координат от времени, например х =
f(t).
В этом случае траектория движения совпадает с отрезком
координатной оси, при этом v= дельта r/дельта t.
Для этого вида движения скорость есть величина постоянная.
Следовательно, vx = дельта x/дельта t
есть величина постоянная. Ускорение при равномерном движении
равно нулю, поскольку равно нулю изменение скорости. Таким
образом, уравнение движения будет иметь вид:
х = х0 + vxt.
Этот вид движения отображается следующими графиками. Графики 1
и 2 отображают движение материальных точек при условии
vl > v2, х0 = 0
(рис. 6). Графики 3 и 4 отображают движение материальных
точек, у которых скорости направлены против оси х, при этом
v4 > v3, Х0 =
Х1
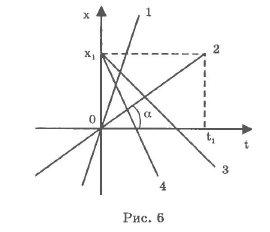
Заметим, что по графику зависимости координаты от времени
можно вычислить скорость движения:
![]()
например vx2=x1/t1, что равно
значению тангенса угла а, образованного графиком х = f(t) и осью
t. Чем больше угол наклона графика к оси времени, тем больше
скорость движения точки. График зависимости скорости от времени
может быть рассмотрен для двух случаев: v = f1(t) и
vx = f2(t).
В первом случае график всегда имеет положительную ординату, во
втором случае vх может быть меньше нуля (как всякая
проекция вектора).
На рис. 7 движение 2 осуществляется с большей скоростью, чем
движение 1. На рис. 8 движение 1 осуществляется с меньшей
скоростью, чем движение 2, а движение 3 – с самой большей.
Следует отметить, что движение 2 и 3 при этом осуществлялось в
направлении, обратном выбранному направлению оси Ох.
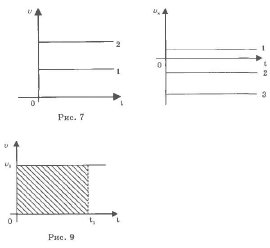
Укажем, как можно определить перемещение, если имеется график
зависимости vх = f1(t) или v =
f2(t).
Исходя из формулы и = дельта x/дельта t,
получим: Ах = v*дельта t.
Как известно, для прямолинейного движения изменение координаты
равно пройденному пути: Ах = s.
Для случая, изображенного на рис. 9, s =
v1дельтаt1, что в геометрической
интерпретации означает: перемещение численно равно площади,
ограниченной осью ординат (Оv), осью абсцисс (Ot), графиком
скорости (v) и ординатой времени (t1).
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В физике следует различать траекторию, путь и перемещение.
Определение 1
Траектория – форма линии, описываемая телом. Ее длина представляет собой путь и является скалярной величиной. Перемещением же называется вектор, соединяющий точки начала и конца пути, и направленный от начала к концу.
Длина пути измеряется в системе СИ в метрах, в СГС (сантиметр, грамм, секунда) – в сантиметрах. Применяются и другие единицы измерения длины, в том числе внесистемные (дюйм, фут, ярд, миля и т.д.).
При движении без ускорения путь равен произведению скорости на расстояние:
$S = v cdot (t_2 – t_1) = v cdot Delta t$,
где $v_0$ – скорость тела, $t_2$ — момент времени окончания движения, $t_1$ — момент времени начала движения, $Delta t$ – время движения. График зависимости пути от времени на координатной плоскости в случае такого, называемого равномерным, движения является прямой линией.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Замечание 1
Поскольку скорость – векторная величина, равномерным можно считать только движение по прямой, т.к. при изменении направления движения вектор не остается неизменным даже при сохранении его длины.
Если равноускоренное движение начато с нулевой скорости и известно ускорение, то формула пути имеет вид
$S = frac{a cdot t^{2}}{2}$
где $a$ – ускорение тела.
Объединив два условия, получим общую формулу нахождения пути при равноускоренном движении с произвольной начальной скоростью:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$.
Если движение не равномерное и известна средняя скорость движения, то путь можно выразить и другим способом:
$S = v_{ср.} cdot Delta t$,
где $v_{ср.}$ – средняя скорость движения.
На практике движение бывает равномерным или равноускоренным лишь на небольших фрагментах пути, поэтому для вычисления его длины траекторию разбивают на участки, где тело движется по простым закономерностям, вычисляют длину каждого из них и суммируют. Если известна траектория, то ее разбивают на фрагменты, каждый из которых имеет простую геометрическую форму. Сложив их длины, можно найти путь.
Пример 1
Найти путь, пройденный при движении с ускорением 2 $м/с^2$ в течение 20 с, если скорость на момент начала измерения была равна 10 м/с.
Подставим в формулу численные значения:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$
$S = frac{2 cdot 20^2}{2} + 10 cdot 20 = 600 м$.
Ответ: длина пути составила 600 метров.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
