Формула линейной скорости в физике
Формула линейной скорости
Скорость движения тела ($overline{v}$) называют линейной, если хотят подчеркнуть ее отличие от угловой скорости ($omega $). Чаще величину $overline{v}$, являющуюся векторной величиной, основной характеристикой движения тела, называют просто скоростью.
Формула мгновенной скорости
Определение
Мгновенная скорость (обычно просто скорость) – это векторная величина, равная первой производной от радиус-вектора ($overline{r}$), определяющего положение движущейся материальной точки, по времени ($t$):
[overline{v}=frac{doverline{r}}{dt}=dot{overline{r}}left(1right).]
Представим вектор $overline{r}$ в декартовой системе координат в виде:
[overline{r}=xleft(tright)overline{i}+yleft(tright)overline{j}+zleft(tright)overline{k}left(2right),]
где $overline{i}$; $overline{j}$; $overline{k}$ – единичные орты соответствующих осей координат, постоянные во времени, при этом формулой скорости можно считать выражение:
[overline{v}=overline{i}frac{dx}{dt}+overline{j}frac{dy}{dt}+overline{k}frac{dz}{dt}left(3right).]
Проекциями вектора скорости на оси координат X, Y,Z являются:
[left{ begin{array}{c}
v_x=frac{dx}{dt}, \
v_y=frac{dy}{dt} \
v_z=frac{dz}{dt}. end{array}
right.(4),]
Величину (модуль) скорости найдем в соответствии с формулой:
[v=sqrt{v^2_x+v^2_y{+v}^2_z}.]
Если движение задается при помощи параметров траектории, что означает: известны траектория и функция пути от времени ($s(t)$); путь отсчитывают от точки траектории, которую считают начальной; каждая точка траектории характеризуется своей величиной $s$; радиус – вектор является функцией от $s,$ и траекторию можно задать при помощи уравнения:
[overline{r}=overline{r}left(sright)left(5right),]
в таком случае в формуле (1) $overline{r}left(tright)$ будем рассматривать как сложную функцию: $overline{r}left[sleft(tright)right]$, формулой скорости станет:
[overline{v}=frac{doverline{r}}{dt}=frac{doverline{r}}{ds}frac{ds}{dt}left(6right).]
Величина $Delta s$ – это расстояние между двумя точками по траектории движения тела. Модуль $left|Delta overline{r}right|$ – расстояние между этими точками по кратчайшему направлению – прямой. При сближении рассматриваемых двух точек разница между $Delta s$ и $left|Delta overline{r}right|$ уменьшается. Имеем:
[frac{doverline{r}}{ds}={mathop{lim }_{Delta sto 0} frac{Delta overline{r}}{Delta s} }={mathop{lim }_{Delta sto 0} frac{Delta overline{r}}{left|Delta overline{r}right|} }cdot frac{left|Delta overline{r}right|}{Delta s}=overline{tau }left(7right),]
где $overline{tau }$ – единичный вектор, касательный к траектории движения материальной точки. Кроме этого:
[frac{ds}{dt}=v(8)]
модуль скорости движения точки по траектории. Уравнение (6) представим как:
[overline{v}=frac{doverline{r}}{dt}=frac{ds}{dt}overline{tau }=voverline{tau }left(9right).]
Формула (9) показывает, что мгновенная скорость направлена по касательной к траектории движения тела (материальной точки).
Формулы средней скорости
Вектор средней скорости ($leftlangle overline{v}rightrangle $) при движении между двумя точками определяют как:
[leftlangle overline{v}rightrangle left(t,t+Delta tright)=frac{Delta overline{r}}{left|Delta overline{r}right|}frac{left|Delta overline{r}right|}{Delta t}=frac{Delta overline{r}}{Delta t}left(10right),]
где в скобках у вектора средней скорости указан промежуток времени, для которого найдена средняя скорость; $Delta overline{r}$ – вектор перемещения точки; $Delta t$- время движения.
При неравномерном движении средняя скорость для разных промежутков времени не одинакова. Устремляя $Delta t$ к нулю, мы получим, что средняя скорость стремится к величине мгновенной скорости.
Иногда при вычислении средней скорости (ее называют средне путевой) применяют другую формулу:
[leftlangle vrightrangle =frac{s}{t}left(11right),]
где $s$- весь путь пройденный точкой; $t$ – все время ее движения. В этом случае средняя скорость – это скаляр.
Формулы линейной скорости при движении разных видов
Если тело движется равномерно, скорость постоянная величина. Ее формулой считают:
[v=frac{s}{t}left(12right),]
где $s$ – путь; $t$ – время движения. При равномерном прямолинейном движении у скорости постоянным является не только величина, но и направление, при этом записывают:
[overline{v}=const.]
Если известно ускорение материальной точки как функции от времени ($overline{a}(t)$) и начальная скорость движения тела (${overline{v}}_0(t=0)$), скорость находят, используя формулу:
[overline{v}={overline{v}}_0+intlimits^{t’}_0{overline{a}(t)}dt left(13right).]
Если тело перемещается с постоянным ускорением (при $overline{a}=const$) скорость равна:
[overline{v}={overline{v}}_0+overline{a}t left(14right).]
Угловая и линейная скорости
При движении по кривой вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($omega $), которая характеризует быстроту изменения угла поворота $varphi $:
[omega =frac{dvarphi }{dt}left(15right).]
Связь между линейной и угловой скоростями определена формулой:
[v=Romega left(16right),]
где $R$ – радиус кривизны траектории, по которой движется точка.
Примеры задач с решением
Пример 1
Задание. Положение материальной точки, задано радиус-вектором $overline{r }left(tright),$ который является функцией времени: $overline{r }left(tright)={2t}^4overline{i}+t^2overline{j},$ где $overline{i}$ и $overline{j}$ – единичные векторы осей X и Y (рис.1). Чему равен модуль скорости точки в момент времени $t=1$c?
Решение. В качестве основы для решения задачи воспользуемся формулой скорости:
[overline{v}={frac{doverline{r}}{dt} left(1.1right). }]
Подставим в выражение (1.1) $overline{r }left(tright)=t^4overline{i}+3t^2overline{j},$ получим:
[overline{v}=frac{d}{dt}left({2t}^4overline{i}+t^2overline{j}right)=8t^3overline{i}+2toverline{j} left(1.2right).]
Из уравнения (1.2) имеем:
[left{ begin{array}{c}
v_x=8t^3 \
v_y=2t end{array}
right.left(1.3right).]
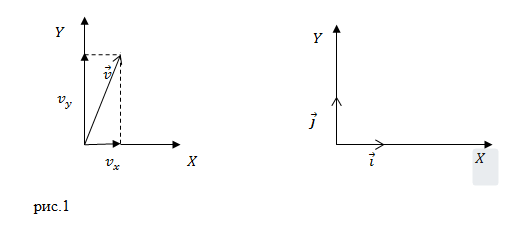
Используя теорему Пифагора, величину скорости вычислим как:
[v=sqrt{v^2_x+v^2_y}=sqrt{{left(8t^3right)}^2+{left(2tright)}^2}=sqrt{64t^6+{4t}^2}=sqrt{68}(frac{м}{с}).]
Ответ. $v=sqrt{68}frac{м}{с}$
Пример 2
Задание. С какой скоростью должен лететь самолет с востока на запад на широте $varphi $, чтобы за окном иллюминатора всегда было светло? Радиус Земли считать равным R.
Решение. Сделаем рисунок.
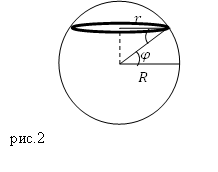
Самолет летит по окружности (рис.2), радиус которой найдем как:
[r=R{cos varphi }left(2.1right).]
Для того чтобы не наступала ночь, тело должно двигаться с угловой скоростью, которая равна скорости вращения Земли вокруг своей оси ($omega $). Для вычисления скорости движения самолета воспользуемся формулой:
[v=omega r=omega R{cos varphi left(2.2right). }]
Угловую скорость вращения Земли найдем, зная, что период вращения Земли составляет 24 ч ($T=24 ч$), следовательно, величину угловой скорости вращения Земли можно считать известной и равной:
[omega =frac{2pi }{T}left(2.3right).]
Окончательно получим, скорость движения самолёта равна:
[v=frac{2pi }{T}R{cos varphi . }]
Ответ. $v=frac{2pi }{T}R{cos varphi }$
Читать дальше: формула модуля равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Наталья Николаевна Пушкина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Средняя скорость
Если тело перемещается неравномерно, то описывая его движение в качестве одного из параметров можно воспользоваться средней скоростью движения на отдельных отрезках пути. Но такое описание дает очень приближенную, грубую характеристику перемещения. Поскольку находя средние скорости, мы проводим замену неравномерного движения на движение с постоянной скоростью на избранных отрезках пути, думая, что скорость изменяется скачкообразно при переходе от одного отрезка времени к другому. Графиком пути, отражающем перемещение тела, с постоянной скоростью, отличающейся на разных временных отрезках, станет ломаная линия, имеющая звенья с различным наклоном.
Допустим, что материальная точка перемещается вдоль прямой линии, которая не совпадает с осями координат. При этом ее положение определяет радиус- вектор $vec r_1$, соответствующий моменту времени $t_1$. В момент времени $t_2$ положение материальной точки в пространстве определяет вектор $vec r_2$.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Вектор перемещения нашей материальной точки определим как:
$Delta vec r=vec r_2-vec r_1(1).$
Определение 1
Средняя скорость материальной точки будет определена выражением:
$ vec v_{sr}=frac{Delta vec r}{Delta t}=frac{vec r_2-vec r_1}{t_2-t_1}(2).$
Из формулы (2) видно, что в ней происходит деление вектора на скаляр, в результате мы имеем вектор, направление которого совпадает с направлением вектора перемещения.
Векторы скорости и перемещения обладают одинаковыми направлениями.
Переход от средней скорости к мгновенной скорости
В выражении (2) средняя скорость найдена для отрезка времени, равного $Delta t$. Разделим данный временной отрезок на более мелкие. Если материальная точка перемещается неравномерно, то вновь найденные средние скорости будут отличаться, от средней скорости для всего отрезка $Delta t$. Уменьшим временной отрезок $Delta t$, станут меньше и отрезки времени внутри него. Средние скорости в уменьшенных промежутках времени будут отличаться от средней скорости на всем отрезке времени, но величина различия станет меньше.
«Мгновенная скорость» 👇
Устремим рассматриваемый промежуток времени к нулю (∆t→0), средняя скорость при этом устремится к предельному значению, которое называют мгновенной скоростью.
Определение 2
Мгновенной скоростью или скоростью в данный момент времени называют векторную величину, равную:
$vec v(t)= frac {dvec r}{dt}(3).$
Если тело перемещается равномерно, то мгновенная скорость его движения в каждый момент времени совпадает со скоростью этого движения. Говорят, что мгновенная скорость равномерного движения является постоянной.
Мгновенная скорость неравномерного перемещения – это переменный параметр, который принимает разные значения для разных моментов времени. При этом мгновенную скорость можно считать изменяющейся непрерывно на всем отрезке времени, на котором рассматривается движение.
Мгновенную скорость в каждый момент времени можно определить как тангенс угла наклона касательной к кривой – траектории движения в рассматриваемой точке.
Компоненты вектора мгновенной скорости в декартовой системе координат
В декартовой системе координат радиус-вектор запишем как:
$vec r(t)=x(t)vec i+y(t)vec j+z(t)vec k (4)$,
принимая во внимание, что единичные орты ($vec i ; vec j; vec k$) не изменяются во времени, и используя определение мгновенной скорости (3), получаем:
$vec v(t)=frac{dx}{dt}vec i+frac{dy}{dt}vec j+frac{dz}{dt}vec k (5).$
Из формулы (5) мы видим, что составляющие вектора скорости в декартовой системе координат задаются выражениями:
$ v_x=frac{dx}{dt} (6),$
$ v_y=frac{dy}{dt} (7),$
$ v_z=frac{dz}{dt} (8).$
При этом величину мгновенной скорости можно найти как:
$ v^2=v_x^2+v_y^2+v_z^2 (9).$
Направление мгновенной скорости
Будем описывать движение материальной точки через параметры траектории. При этом нам известны траектория движения точки и связь пути ($s$) и времени $t$. Путь отмеряется по траектории, от точки траектории, которую мы принимаем за начальную. При этом любая точка траектории характеризуется собственной величиной $s$. Из сказанного выше следует, что радиус-вектор – это функция от $s$, траекторию зададим уравнением:
$vec r = vec r(s)(10)$.
Получаем, что в определении мгновенной скорости (3) мы можем считать радиус – вектор как сложную функцию ($vec r(s(t))$). При этом ее производную найдем, применяя правило дифференцирования сложной функции:
$vec v=frac{dvec r}{dt}=frac{dvec r}{ds}frac{ds}{dt}(11)$,
где по определению мгновенной скорости ее величина равна: $v=frac{ds}{dt}$.
Обозначим $Delta s$ – расстояние между парой точек по траектории; $|Delta vec r|$– расстояние между рассматриваемыми точками по кратчайшему расстоянию (прямой). При сближении наших точек разница между $Delta s$ и $|Delta vec r|$ уменьшается, запишем:
$frac{dvec r}{ds}=lim_{Delta sto 0} (frac {Delta vec r}{Delta s})=lim_{Delta sto 0}(frac{Delta vec r}{|Delta r|}frac {|Delta r|}{Delta s})=vec tau (12).$
где $vec tau$ – единичный вектор, являющийся касательным к траектории движения точки.
Принимая во внимание сказанное выше выражение (12) для мгновенной скорости можно записать как:
$vec v=vvec tau$(13).
Из формулы (13) становится очевидно, что мгновенная скорость направлена по касательной к траектории движения материальной точки.
Рассматривая направления мгновенной скорости движения материальной точки подчеркнем, что:
- Мгновенная скорость материальной точки перемещающейся по прямой – это вектор, который направлен по траектории ее движения.
- При перемещении материальной точки по криволинейной траектории вектор мгновенной скорости имеет направление по касательной к траектории движения точки.
Скорость при равнопеременном движении
Самым простым способом неравномерного движения является равнопеременное перемещение тела, движение с постоянным ускорением. Это движение бывает:
- равноускоренным, если скорость и ускорение имеют одинаковые направления, при этом величина скорости увеличивается;
- равнозамедленное, при противоположном направлении скорости и ускорения, в этом случае скорость по модулю уменьшается.
При равнопеременном движении скорость в любой момент времени можно вычислить, если использовать выражение:
$vec v(t)=vec v_0+vec a bullet t (14),$
где $vec v_0$ – начальная скорость движения точки; $vec a$ – постоянное ускорения точки.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Для описания
движения выбирают тело отсчета – это
произвольны выбор тела относительно
которых определяется положение других
движущихся тел.
Система
координат
– это система связанная с телом отсчета
(в противном случае декартовая система
координата)
Система
отсчета –
это совокупность тел отсчета связанная
с ним системой координат и синхронизированных
между сомой часов.
Положение точки А
характеризуется 3 координатами
При движении
материальной точки координаты будут
изменяться
Уравнение
движения материальной точки
x=x(f)
y=y(f)
z=z(f)
r=r(f)
6.Скорость (средняя. Ее модуль, мгновенная скорость и ее модуль). Путь, траектория, вектор перемещения, длинна пути.
Траектория
– это линия
отсчитываемая движущиеся материальной
точкой то есть выбор системы координат.
Траектория в разл.
системе отсчета может быть разная если
траектория деления
прямая линия
–прямолинейной
Кривая линия –
криволинейной
Если тело находится
в точке А потом перемещается в точку В
то
дельтаr=r0-r
Это приращения
вектора r
за промежуток времени дельта ф
Длинна пути
дельта s(t)
– это пройденный промежуток времени
s
– скалярный вектор
Если все точки
траектории лежат в одной плоскости то
движение называется плоским
Скорость
– векторная
величина определяющая как быстроту
движения так и его направление в данный
момент времени.
Средняя
скорость
– векторная величина определяемая
дельта r
вращения к прошедшему времени вращения.
<v>=дельта
r/дельта
t
Направление вектора
средней
скорости
<v>=|<v>|=дельта
r/дельта
t
= |дельта r/дельта
t|=
дельта s/дельта
t
Мгновенная
скорость
v
– это векторная величина определяемая
первой производной r
вектора движущейся точки ко времени
v=lim
дельта r/дельта
t
(при t
стрем. к 0)= дельта r/дельта
t
Векторные скорости
направлены по касательной к т.А
Модуль
мгновенной скорости
v
v=|v|=|lim
дельта r/дельта
t
(при t
стрем. к 0)|= дельта s/дельта
t
Длинна
пути s
пройденного за промежуток точкой есть
s=интеграл
от t2
до t1
от v(t)dt
(м/с)
7. Ускорение и его составляющее (среднее, мгновенное, нормальное, тангинцеальное, полное ускорение при криволинейном движении)
Ускорение
– есть
характеристика ее равномерного движения
и определяет быстроту
изменения скорости
как по модулю или по направлению.
Существует понятие движение по окружности
с ускорением.
Среднее
ускорение
– это векторная величина равная отношению
изменения скорости к интервалу времени
<a>=
дельта v/дельта
t
Мгновенное
ускорение
а векторная величина определяемое
первой производной скорости ко времени
a=
lim
дельта v/дельта
t
(при t
стрем. к 0)|= дельта v/дельта
t
Составляющее
ускорение может быть
а).Тангенциальным
– характеризует
быстроту изменения скорости по модулю.
Она направлена по касательной к траектории
а тангенциальное
дельта v/дельта
t
б).Нормальное
составляющее
характеризует изменение скорости по
величине и направлению, характеризует
быстроту изменения скорости по
направленности. Она направлена к центру
изменения траектории.
а нормальное дельта
v
в квадрате/дельта r
Тангенциальное
ускорение – постоянная величина .
Нормальное ускорение
=0 появляется при движении по окружности.
Криволинейное
равнопеременное движение
Полное ускорение
при криволинейном геометрическом
движении
нормальное+тангенциальное
движение
а (м/с2)
8.Угловая скорость,
период вращения, углы поворота, частота,
скорость. Вращательное
движение твердого тела – движение при
котором все точки движущейся по окружности
центры которых лежат на одной прямой
называемой осью вращения.
Существует угловая
скорость
векторная величина определяемая
следующим образом.
w=lim
дельта f/дельта
t
(при t
стрем. к 0)|= дельта f/дельта
t
Пер. угла поворота
ко времени
где df
– вектор
Элементы угла
поворота df
рассчитываются как вектора
Модуль вектора df
равен углу
поворота,
а что направление совпадает с направлением
поступательного движения острия винта
головка которого вращается в в направлении
движения точки по окружности что
подчиняется правилу правого винта (если
точка движется по окружности против
часовой стрелки).
Поэтому угловая
скорость будет направлена по оси движения
Еденица w=1
рад/с
Период
вращения
время за которое точка совершает полный
оборот
w=2пи/Т
где Т-период
Линейная
скорость
точка движущейся по окружности
Линейная скорость
v=lim
дельта s/дельта
t
(при t
стрем. к 0)=lim
R*дельта
f/дельта
t
(при d
стрем. к 0)
v=Rw
Частота
вращения
– это число полных оборотов совершаемых
телом в единицу времени
Число полных
оборотов совершаемом за единицу времени
назывеется частотой вращения
n=1/T=w/2пи
w=2пи*n
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вектор дельта r это
В кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси.
1. Векторный способ.
В этом способе положение материальной точки `A` задаётся с помощью так называемого радиус-вектора `vecr`, который представляет собой вектор, проведённый из точки `O`, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку `A` (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени `vecr=vecr(t)`.
Геометрическое место концов радиус-вектора `vecr(t)` называют траекторией точки `A`.
В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка `A` после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.
Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени `Delta t` тело (точка `A`) переместилось из начального положения `1` с радиус-вектором `vec r_1` в конечное положение `2` с радиус-вектором `vec r_2` (рис. 2). Приращение `Deltavec r` радиус-вектора тела в таком случае равно: `Deltavec r = vec r_2- vec r_1`.
Вектор `Deltavec r`, соединяющий начальное и конечное положения тела, называют перемещением тела.
Отношение `Delta vec r//Delta t` называют средней скоростью (средним вектором скорости) `vec v_”cp”` тела за время `Delta t`:
`vecv_”cp”=(Deltavecr)/(Delta t)` (1)
Вектор `vecv_”cp”` коллинеарен и сонаправлен с вектором `Deltavec r`, так как отличается от последнего лишь скалярным неотрицательным множителем `1//Delta t`.
Предложенное определение средней скорости справедливо для любых значений `Delta t`, кроме `Delta t=0`. Однако ничто не мешает брать промежуток времени `Delta t` сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени `t` или в конкретной точке траектории. С этой целью промежуток времени `Delta t` устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение `Delta vec r`. При этом отношение `Deltavec r//Delta t` стремится к определённому значению, не зависящему от `Delta t`.
Величина, к которой стремится отношение `Deltavec r//Delta t` при стремлении `Delta t` к нулю, называется мгновенной скоростью`vec v`:
`vec v =(Delta vec r)/(Delta t)` при `Delta t -> 0`.
Теперь заметим, что чем меньше `Delta t`, тем ближе направление `Deltavec r` к направлению касательной к траектории в данной точке. Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела.
В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости `vec v` тела (материальной точки).
Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения. Его определяют через отношение приращения вектора скорости `Delta vec v` тела к промежутку времени `Delta t`, в течение которого это приращение произошло.
Ускорением `veca` тела называется величина, к которой стремится отношение `Delta vec v//Delta t` при стремлении к нулю знаменателя `Delta t`:
`vec a =(Delta vec v)/(Delta t)` при `Delta t -> 0` (2)
При уменьшении `Delta t` ориентация вектора`Delta vec v` будет приближаться к определённому направлению, которое принимается за направление вектора ускорения `vec a`. Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости!
Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (`”м”//”с”`) и метр на секунду в квадрате ( `”м”//”с”^2`).
2. Координатный способ.
В этом способе положение материальной точки `A` на плоскости в произвольный момент времени `t` определяется двумя координатами `x` и `y`, которые представляют собой проекции радиус-вектора $$ overrightarrow$$тела на оси `Ox` и `Oy` соответственно (рис. 3). При движении тела его координаты изменяются со временем, т. е. являются функциями `t`: $$ x=xleft(tright)$$ и $$ y=yleft(tright)$$. Если эти функции известны, то они определяют положение тела на плоскости в любой момент времени. В свою очередь, вектор скорости $$ overrightarrow$$ можно спроецировать на оси координат и определить таким образом скорости $$ _$$ и $$ _$$ изменения координат тела (рис. 4). В самом деле $$ _$$ и $$ _$$ будут равны значениям, к которым стремятся соответственно отношения `Delta x//Delta t` и `Delta y//Delta t` при стремлении к нулю промежутка времени `Delta t`.
3. Естественный (или траекторный) способ.
Этот способ применяют тогда, когда траектория материальной точки известна заранее. На заданной траектории `LM` (рис. 5) выбирают начало отсчёта – неподвижную точку `O`, а положение движущейся материальной точки `A` определяют при помощи так называемой дуговой координаты `l`, которая представляет собой расстояние вдоль траектории от выбранного начала отсчёта `O` до точки `A`. При этом положительное направление отсчёта координаты `l` выбирают произвольно, по соображениям удобства, например так, как показано стрелкой на рис. 5.
Движение тела определено, если известны его траектория, начало отсчёта `O`, положительное направление отсчёта дуговой координаты `l` и зависимость $$ lleft(tright)$$.
Следующие два важных механических понятия – это пройденный путь и средняя путевая скорость.
По определению, путь `Delta S` – это длина участка траектории, пройденного телом за промежуток времени `Delta t`.
Ясно, что пройденный путь – величина скалярная и неотрицательная, а потому его нельзя сравнивать с перемещением `Delta vec r`, представляющим собой вектор. Сравнивать можно только путь `Delta S` и модуль перемещения `
|Delta vecr|`. Очевидно, что `Delta S >=|Deltavec r|`.
Средней путевой скоростью `v_”cp”` тела называют отношение пути `Delta S` к промежутку времени `Delta t`, в течение которого этот путь был пройден:
`v_”cp”=(Delta S)/(Delta t)` (3)
Определённая ранее средняя скорость `v_”cp”` (см. формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как `Deltavec r` отличается от `Delta S`, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения `Delta t`. Само слово «средняя» означает усреднение по времени.
Городской троллейбус утром вышел на маршрут, а через 8часов, проехав в общей сложности `72` км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость `vec v_”cp”` и средняя путевая скорость `v_”cp”` троллейбуса?
Поскольку начальное и конечное положения троллейбуса совпадают, то его перемещение `Delta vecr` равно нулю: `Deltavecr=0`, следовательно, `vecv_”ср”=Deltavecr//Deltat=0` и `|vecv_”ср”|=0`. Но средняя путевая скорость троллейбуса не равна нулю:
`v_”cp”=(Delta S)/(Delta t)=(72 “км”)/(8 “ч”)=9 “км”//”ч”`.
Путь и перемещение
При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь – длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь – это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
где $x_1$ – координата начального положения тела; $x_2$ – конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
[Delta s=vt left(2right),]
где $t$ – время движения тела.
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
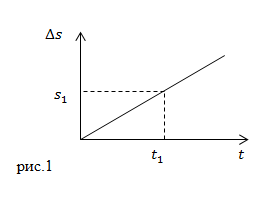
Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку $<Delta s>_1$, которая соответствует пройденному пути за время от $t=0 c$ до $t_1$.
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
[Delta overline=overlineleft(t+Delta tright)-overlineleft(tright)left(3right).]
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки – это перемещение ($Delta overline$).
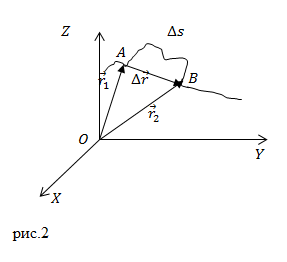
В декартовой системе координат радиус-вектор точки представляют в виде:
где $overline$, $overline$,$ overline$ – единичные орты осей X,Y,Z. Тогда $Delta overline$ равен:
[Delta overline=left[xleft(t+Delta tright)-xleft(tright)right]overline+left[yleft(t+?tright)-yleft(tright)right]overline+left[zleft(t+?tright)-zleft(tright)right]overlineleft(5right).]
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
[left|Delta overlineright|=Delta s left(6right).]
Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overlineright|$ или просто $Delta r$ (без указания стрелки).
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
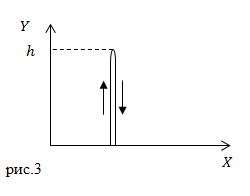
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь – длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
Перемещение – направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
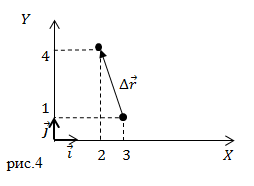
Радиус – вектор начальной точки запишем как:
Радиус – вектор конечной точки имеет вид:
Вектор перемещения представим как:
Из формулы видим, что:
[Delta r_x=-1;;Delta r_y=3. ]
Ответ: $Delta r_x=-1;;Delta r_y=3 $
Перемещение. Перемещение точки
Понятие перемещения имеет важнейшее значение в кинематике.
Мы будем рассматривать перемещение точки.
Зададим положение точки с помощью радиус-вектора.
Вектор перемещения равен приращению радиус-вектора.
на картинке дельта «эр» – это и есть вектор перемещения.
По правилу сложения векторов имеем:
а это значит, что вектор перемещения равно приращению радиус-вектора.
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/fizika/fizika_88_put_i_peremeshhenie.php
[/spoiler]
Как найти дельта S и дельта t , если просто s = 0, 58м ; 0, 21м ; 0, 07м t = 0.
5с ; 0, 3с ; 0, 1с и напишите пжл формулу.
Вы перешли к вопросу Как найти дельта S и дельта t , если просто s = 0, 58м ; 0, 21м ; 0, 07м t = 0?. Он относится к категории Физика,
для 5 – 9 классов. Здесь размещен ответ по заданным параметрам. Если этот
вариант ответа не полностью вас удовлетворяет, то с помощью автоматического
умного поиска можно найти другие вопросы по этой же теме, в категории
Физика. В случае если ответы на похожие вопросы не раскрывают в полном
объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части
сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете
ознакомиться с вариантами ответов пользователей.
