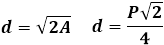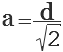Как найти сторону квадратного треугольника
Квадратный треугольник более точно называется прямоугольным треугольником. Соотношения между сторонами и углами этой геометрической фигуры подробно рассматриваются в математической дисциплине тригонометрии.
Вам понадобится
- – лист бумаги;
- – ручка;
- – таблицы Брадиса;
- – калькулятор.
Инструкция
Найдите сторону прямоугольного треугольника с помощью теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов: с2 = a2+b2 , где с – гипотенуза треугольника, a и b – его катеты. Чтобы применить это уравнение, нужно знать длину любых двух сторон прямоугольного треугольника.
Если по условиям заданы размеры катетов, отыщите длину гипотенузы. Для этого с помощью калькулятора извлеките квадратный корень из суммы катетов, каждый из которых предварительно возведите в квадрат.
Вычислите длину одного из катетов, если известны размеры гипотенузы и другого катета. При помощи калькулятора извлеките квадратный корень из разности гипотенузы в квадрате и известного катета, также возведенного в квадрат.
Если в задаче заданы гипотенуза и один из прилежащих к ней острых углов, используйте таблицы Брадиса. В них приведены значения тригонометрических функций для большого числа углов. Воспользуйтесь калькулятором с функциями синуса и косинуса, а также теоремами тригонометрии, которые описывают соотношения между сторонами и углами прямоугольного треугольника.
Найдите катеты при помощи основных тригонометрических функций: a = c*sin α, b = c*cos α, где а – катет, противолежащий к углу α, b – катет, прилежащий к углу α. Подобным образом посчитайте размер сторон треугольника, если заданы гипотенуза и другой острый угол: b = c*sin β, a = c*cos β, где b – катет, противолежащий к углу β, а – катет, прилежащий к углу β.
В случае, когда известен катет a и прилежащий к нему острый угол β, не забывайте, что в прямоугольном треугольнике сумма острых углов всегда равна 90°: α + β = 90°. Отыщите значение угла, противолежащего к катету а: α = 90° – β. Или воспользуйтесь тригонометрическими формулами приведения: sin α = sin (90° – β) = cos β; tg α = tg (90° – β) = ctg β = 1/tg β.
Если известен катет а и противолежащий к нему острый угол α, при помощи таблиц Брадиса, калькулятора и тригонометрических функций вычислите гипотенузу по формуле: c=a*sin α, катет: b=a*tg α.
Видео по теме
Источники:
- Как найти стороны прямоугольного треугольника по катету и острому углу
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.
Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
– Все стороны квадрата равны (от ромба)
– Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)
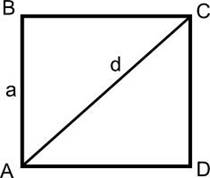
Если провести диагональ квадрата, то она образует с его сторонами не просто прямоугольный треугольник (как в прямоугольнике), но равнобедренный прямоугольный треугольник, который по теореме Пифагора будет связывать всего два параметра – диагональ квадрата и его сторону. Стороны квадрата будут катетами для треугольника, а диагональ гипотенузой.
a2+b2=c2
a2+b2=d2
2a2=d2
Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:
d=√(2a2)
d=a√2
Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.
Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.
Формулы диагонали квадрата через площадь, периметр
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Диагональ, диаметр описанной окружности (M) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{frac{M^{2}}{2}}) = (sqrt{frac{10^{2}}{2}}) = 7.07
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{7.07}{2}) = 3.54
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{10}{2}) = 5
Периметр (P) = (L*4) = (7.07*4) = 28.28
Площадь (S) = (L^{2}) = (7.07^{2}) = 49.98
Сторона квадрата
Стороны фигур
Четырехугольник, у которого все четыре стороны равны, противоположные — параллельны, а углы — прямые, называется квадратом. Диагональ квадрата (d) делит его на 2 одинаковых прямоугольных треугольника, у которых гипотенузой является диагональ (d) квадрата, а катетами — две одинаковых стороны квадрата (а). Как известно по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. d2 = а2 + а2 = 2а2.
Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.
Расчет стороны квадрата через диагональ
Расчет стороны квадрата через площадь
Как найти сторону квадрата если известна диагональ?
В прошлый раз мы вывели формулу, как найти диагональ в квадрате.
Теперь нам нужно лишь вывести нашу формулу в обратную сторону.
Я не буду здесь заново выводить формулу, по которой можно найти диагональ квадрата. Вот она:
d = √2a²
Где d – диагональ квадрата,
√ – корень,
a² – сторона в квадрате.
Теперь из формулы подсчета размера диагонали d = √2a² , нам нужно вывести значение “а” – стороны квадрата.
Возведем эту формулу в квадрат, у нас получится:
d² = 2a²
Далее разделим нашу формулу на 2, у нас получится вот так:
d²/2 = a²
Для удобства чтения поменяем местами значения.
a² = d²/2
Ну и далее извлечём из всего корень! И получим: что сторона квадрата равна корню из квадрата диагонали деленного на 2.
a = √d²/2
Написать что-нибудь…
найти сторону квадрата по диагонали
сторона квадрата через диагональ
сторона квадрата по диагонали
найти сторону квадрата по диагонали