Диагональ параллелограмма – это отрезок, соединяющий противоположные вершины фигуры. В зависимости от
вида геометрической фигуры диагональ обладает важными свойствами, на которые основываются базовые
правила и формулы. Рассмотрим подробнее, как найти длину данного отрезка, построенного в
параллелограмме с равными сторонами, т.е. ромбе.
- Диагональ ромба через сторону и другую известную
диагональ - Длинная диагональ ромба через сторону и острый угол
- Длинная диагональ ромба через сторону и тупой угол
- Короткая диагональ ромба через сторону и острый угол
- Короткая диагональ ромба через сторону и тупой угол
- Длинная диагональ ромба через короткую диагональ и тупой
угол - Короткая диагональ ромба через длинную диагональ и острый
угол - Диагональ ромба через площадь ромба и другую известную
диагональ
Диагональ ромба через сторону и другую известную диагональ
В случае, если в ромбе известны значения одной диагонали (d) и стороны (a) фигуры, прийти к
определению длины второго отрезка будет несложно, благодаря тождеству параллелограмма, которое
гласит, что сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:
d = √(4a² — d²)
где a — сторона, d — известная диагональ.
Цифр после
запятой:
Результат в:
Пример. Дан ромб с диагональю равной 6 мм и стороной, длина которой 5 мм. Нужно
найти вторую диагональ ромба. d = √(4 * 5² — 6²) = √(4 * 25 — 36) = √(100 — 36) = √64 = 8 мм
– длина неизвестной диагонали.
Как найти длину большей диагонали через сторону и острый угол
Найти величину длинной диагонали можно по формуле:
d = a * √(2 + 2 * cos α)
где a — сторона, cos α — острый угол.
Цифр после
запятой:
Результат в:
Проведенный отрезок, который соединяет противоположные вершины фигуры, делит ее на равнобедренные
треугольники. По свойствам равнобедренного треугольника косинус углов при основании равен половине
основания (в данном случае диагонали), деленного на боковую сторону (сторону ромба).
Пример. Острый угол между сторонами ромба длиной 6 см равен 45 градусам. Найти
биссектрису острого угла ромба (в данном случае диагональ). d = 6 * √(2 + 2 * cos 45°) = 6 * √(2 + 2 * √2 / 2) = 6 * √(2 + 2 * 0,7) = 11см
– длинна неизвестного отрезка.
Как найти длину большей диагонали через сторону и известное значение тупого угла
Как уже известно, построенная диагональ в ромбе, делит его на 2 равнобедренных треугольника. Если
дополнить картину второй проведенной диагональю, получится прямоугольный треугольник. Косинус
половинки тупого угла (c) это отношение прилежащего катета к гипотенузе (стороне ромба a). На
основании всех этих свойств можно прийти к простой формуле нахождения нужной диагонали через сторону
ромба (в данном случае гипотенузу) и косинус тупого угла:
d = a * √( 2 — 2 * cos β)
где a — сторона, cos β — тупой угол
Цифр после
запятой:
Результат в:
Пример. Дан ромб со стороной 4,65 м, величина тупого угла которого равна 120
градусам. Необходимо найти противолежащую известному углу диагональ. d = 4,65 * √(2 — 2 * cos 120°) = 4,65 * √(2 — 2 * (-0,5) = 8 м
– длина неизвестного отрезка.
Как вычислить длину меньшей диагонали через сторону и острый угол
Так как ситуация аналогична предыдущей (только известный противолежащий угол острый), формула
нахождения короткой диагонали практически ничем не отличается от алгоритма определения длинного
отрезка, соединяющего противолежащие вершины ромба.
d = a * √(2 — 2 * cos α)
где a — сторона, cos α — острый угол
Цифр после
запятой:
Результат в:
Пример. В ромбе со стороной 4,65 м проведена диагональ, которая является основанием
равнобедренного треугольника с углом при вершине равным 52 градусам. Найти основание треугольника
(меньшую диагональ). d = 4,65 * √(2 — 2 * cos 52°) = 4 м.
Короткая диагональ ромба через длинную диагональ и острый угол
Аналогично с предыдущей ситуацией, через тангенс острого угла находим величину неизвестного катета
(половинку искомой диагонали). Упрощенная формула:
d = D * tg (α / 2)
где D — длинная диагональ, α — острый угол
Цифр после
запятой:
Результат в:
Пример. Острый угол ромба, в котором построена диагональ длиной 11 мм, равен 58
градусам. Найти длину второй диагонали. d = 11 * tg 29° = 6 мм – длина
меньшей диагонали ромба.
Короткая диагональ через сторону и тупой угол
Формула для нахождения меньшей диагонали ромба при помощи значения стороны и тупого угла такова:
d = a * √(2 + 2 * cos β)
где a — сторона, cos β — тупой угол
Цифр после
запятой:
Результат в:
Пример. Дан ромб со стороной 4,65 мм, один из углов которого равен 128 градусов, а
меньшая диагональ фигуры – искомая величина. d = a * √(2 + 2 * cos β) = 4,65 * √(2 + 2 * cos 128°) = 4 мм.
Длинная диагональ ромба через короткую диагональ и тупой угол
Длина большей диагонали ромба легко находится по формуле:
D = d * tg (β / 2)
где d — короткая диагональ, β — тупой угол
Цифр после
запятой:
Результат в:
Благодаря теореме Пифагора, зная длину короткой диагонали (половина катета прямоугольного
треугольника) и значение тупого угла ромба (половина которого является углом прямоугольного
треугольника), не составит труда определить значение большей диагонали ромба через тангенс тупого
угла.
Пример. Дан ромб с диагональю 6,5 см, которая является биссектрисой тупого угла
величиной 119 градусов. Нужно найти неизвестную диагональ ромба. D = 6,5 * tg (119 / 2) = 11 см
– искомая величина.
Диагональ ромба через площадь и другую известную диагональ
Найти любую из двух диагоналей ромба можно по формуле:
D = 2 * S / d
где d – длина известного отрезка, а S-площадь фигуры.
Цифр после
запятой:
Результат в:
Пример. Дан ромб с площадью равной 64 см², его диагональ равна 8,5 см. Необходимо
найти длину второго отрезка, соединяющего противолежащие вершины. D = 2 * S / d = 2 * 64 / 8,5 = 15 см.
Ромб относится к плоским выпуклым геометрическим фигурам. Данный вид параллелограмма отличается
равными сторонами, а также тем, что его диагонали при пересечении перпендикулярны друг другу.
Существуют и другие свойства ромба, которые подробно раскрывают смысл указанных выше формул:
- Диагонали, пересекаясь под прямым углом, делятся точкой пересечения пополам. Таким образом, они
всегда разделяют фигуру на 4 прямоугольных треугольника. - Противоположные стороны ромба попарно параллельны.
- Противолежащие углы равны, а смежные – в сумме образуют 180 градусов.
- Диагонали служат биссектрисами всех углов ромба.
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
- Если соединить середины сторон ромба, получится прямоугольник.
- Точка пересечения диагоналей — центр вписанной окружности.
Определение диагонали ромба часто встречается в задачах школьной программы. Найдя данное значение,
можно прийти к искомому результату задания. Через диагональ можно найти стороны ромба, площадь,
периметр и все внутренние углы ромба.
Геометрия в школьной программе включается в себя немалое количество формул, основанных на теоремах и
правилах. Некоторые из которых помогают значительно сократить время для решения задач на контрольной
или при выполнении домашней работы. Данная статья поможет быстро прийти к логическому решению
задания и правильному результату. Знание и применение выше перечисленных формул способствуют умению
решать задачи по геометрии любой сложности.
|
Сумма двух углов ромба равна 120° , а его периметр равен 84.
Вот еще рисунок. Из него видно что мЕньшая диагональ равна 21. 84:4=21 360-120=240 Углы у ромба получаются 120,60,120,60. Диагонали ромба пересекаются под прямым углом. Ответ: меньшая диагональ ромба равна 21. автор вопроса выбрал этот ответ лучшим
RIOLIt 2 года назад Задача решается на основе определений этой фигуры и предположений. Все стороны ромба равны, то есть- по 21, исходя из параметров ромб, в нём два угла острые и два- тупые, значит острые по 60 градусов, тупые по 120, рассмотрев один из четырех треугольников, полученных от пересечения диагоналей, находим их прямоугольными с гипотенузами, равными 21 и половинка малой диагонали равна 10,5, как катет, лежащий против угла в тридцать градусов, получается, что она тоже рана 21 и образовывает равносторонний треугольник, поскольку все углы- по 60 градусов и данный ромб делится диагоналями на два треугольника равносторонних и два равнобедренных- тупоугольных.
ЛенивыйЖирныйКот 2 года назад Из предоставленной записи задания можно только предположить что сумма [двух противоположных] углов равна 120°. Если это так, то получим ромб с острыми углами 60° и тупыми углами 120°. Короткая диагональ поделит ромб на для равносторонних треугольника и стороны его будут равны 0,25 или 1/4 периметра. Отсюда меньшая диагональ равна 21. Знаете ответ? |
Как найти диагональ ромба
У ромба стороны равны и попарно параллельны. Его диагонали пересекаются под прямым углом и делятся точкой пересечения на равные части. Эти свойства легко позволяют найти величину диагоналей ромба.
Инструкция
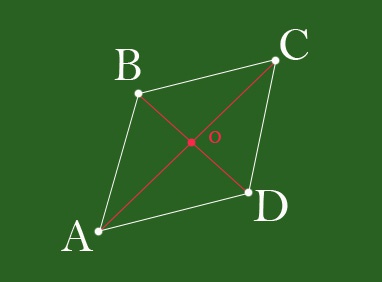
Обозначим вершины ромба буквами латинского алфавита A, B, C и D для удобства обсуждения. Точку пересечения диагоналей традиционно обозначают буквой O. Длину ребра ромба обозначим буквой a. Величину угла BCD, который равен углу BAD, обозначим α.
Найдем величину короткой диагонали. Так как диагонали пересекаются под прямым углом, то треугольник COD является прямоугольным. Половина короткой диагонали OD является катетом этого треугольника и может быть найдена через гипотенузу CD, а также угол OCD.
Диагонали ромба являются также биссектрисами его углов, поэтому угол OCD равен α/2.
Таким образом, OD = BD/2 = CD*sin(α/2). То есть, короткая диагональ BD = 2a*sin(α/2).
Аналогичным образом, из того, что треугольник COD прямоугольный, можем выразить величину OC (а это половина длинной диагонали).
OC = AC/2 = CD*cos(α/2)
Величина длинной диагонали выражается следующим образом: AC =2a*cos(α/2)
Обратите внимание
Ромб с прямыми углами называется квадратом.
Из прямоугольности треугольника COD, как и остальных трех треугольников, образованных диагоналями и сторонами ромба, вытекает еще такое свойство ромба: AC²+BD²=4a²
Полезный совет
Зная диагонали, легко найти площадь ромба. Обычно для этого их и вычисляют. Площадь ромба равна половине произведения его диагоналей.
Источники:
- как найти меньшую диагональ ромба
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Свойства ромба:
1. Ромб – частный случай параллелограмма
2. Противоположные стороны – параллельны
3. Все четыре стороны – равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы диагоналей через сторону и угол, ( D d):
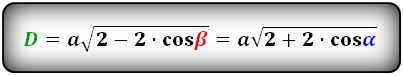
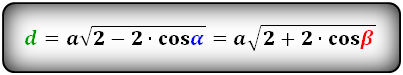
Формулы диагоналей через сторону и половинный угол, (D d):
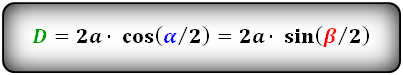
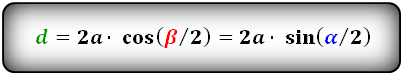
Формулы диагоналей через сторону и другую диагональ, (D d):


Формулы диагоналей через угол и другую диагональ, (D d):
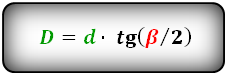
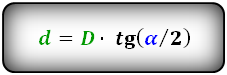
Формулы диагоналей через площадь (D d):
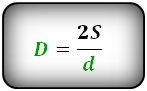
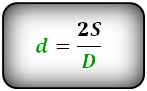
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 23 ноября 2011
-
Обновлено: 13 августа 2021
Plan
- 1 Как найти диагональ ромба?
- 2 Чему равна диагонали ромба?
- 3 Что делают диагонали ромба?
- 4 Как найти углы ромба 8 класс?
- 5 В чем разница между квадратом и прямоугольником?
- 6 Почему ромб не является квадратом?
- 7 Какие стороны у квадрата?
- 8 Когда четырехугольник является ромбом?
- 9 Как доказать что это ромб?
- 10 Как доказать что прямоугольник является квадратом?
- 11 Почему четырехугольник изображенный на рисунке не является квадратом?
- 12 Как доказать что это квадрат?
- 13 Как доказать что фигура является прямоугольником?
- 14 Как доказать что четырехугольник выпуклый?
- 15 Как доказать что Авсд параллелограмм?
- 16 Что такой параллелограмм?
- 17 Как доказать что треугольники равны по первому признаку?
- 18 Как доказать что это равнобедренный треугольник?
- 19 Как найти все стороны параллелограмма?
- 20 Как найти диагональ параллелограмма зная его стороны?
Как найти диагональ ромба?
Как найти диагональ ромба
- Формулы диагоналей ромба через его сторону и угол Меньшая диагональ ромба равна удвоенному произведению стороны на синус половинного острого угла:
- Формулы диагоналей через угол и другую диагональ: и:
- Формулы диагоналей через угол и радиус вписанной окружности: и:
- Шаг 2. Рассмотрим треугольник АОВ.
- Шаг 3.
- Шаг 4.
Чему равна диагонали ромба?
Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.). Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма). Середины четырех сторон ромба являются вершинами прямоугольника.
Как найти короткую диагональ ромба?
е., короткая диагональ BD = 2a*sin(α/2).
Что делают диагонали ромба?
По определению, ромб — это параллелограмм, все стороны которого равны. Свойства ромба: Диагонали ромба перпендикулярны. Диагонали ромба делят его углы пополам.
Как найти углы ромба 8 класс?
Теория:
- Противоположные стороны ромба равны: AB = BC = CD = AD (т.
- Противоположные углы ромба равны: ∢ A = ∢ C; ∢ B = ∢ D.
- Диагонали ромба точкой пересечения делятся пополам: BO = OD; AO = OC.
- Сумма углов, прилежащих к одной стороне ромба, равна 180 ° : ∢ A + ∢ D = 180 ° .
В чем разница между квадратом и ромбом?
У квадрата и ромба все стороны равны, а диагонали пересекаются под прямым углом. Тем не менее, есть некоторые фундаментальные различия. У квадрата все внутренние углы равны и составляют 90 градусов, у ромба равны лишь противоположные углы.
В чем разница между квадратом и прямоугольником?
Квадратом называют параллелограмм, у которого все четыре внутренних угла прямые. Все четыре стороны квадрата равны, то есть имеют одинаковую длину. Прямоугольником называют параллелограмм, внутренние углы у которого прямые, и только противоположные стороны, которые параллельны друг другу, равны.
Почему ромб не является квадратом?
Ромб это четырехугольник с двумя парами параллельных сторон и все стороны у него равны. То есть ромб не всегда будет квадратом, только когда все углы прямые.
Что общего у квадрата и ромба?
Общие свойства квадрата и ромба: У них 4 угла, и у квадрата, и у ромба. Ромб – это четырёхугольная геометрическая фигура, все стороны которой равны. Внутренние углы. У квадрата все углы равны 90 градусов, у ромба данное значение может варьироваться.
Какие стороны у квадрата?
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба. Перечислим свойства квадрата: Все углы квадрата — прямые, все стороны квадрата — равны. Диагонали квадрата равны и пересекаются под прямым углом.
Когда четырехугольник является ромбом?
Если две смежные стороны параллелограмма равны, то данный параллелограмм является ромбом. Если диагонали параллелограмма являются биссектрисами его углов, то данный параллелограмм является ромбом. 4. Если все стороны четырёхугольника равны, то данный четырёхугольник является ромбом.
Как доказать что ромб является квадратом?
Если в прямоугольнике диагонали пересекаются под прямым углом, то этот прямоугольник является квадратом. Если ромба диагонали равны, то этот ромб является квадратом. Если в четырехугольнике все стороны равны и все углы равны, то этот четырехугольник является квадратом.
Как доказать что это ромб?
Признаки ромба используют, чтобы доказать, что некоторый параллелограмм или четырехугольник является ромбом. 1) Если у параллелограмма диагонали взаимно перпендикулярны, то он является ромбом. 2) Если диагональ параллелограмма является биссектрисой его углов, то он является ромбом.
Как доказать что прямоугольник является квадратом?
С помощью этих признаков можно определить, является ли прямоугольник или ромб квадратом.
- Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
- Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
Как доказать что четырехугольник является квадратом?
Если в четырехугольник можно вписать окружность и около него описать окружность, а противолежащие углы равны, то это квадрат. Если в прямоугольник можно вписать окружность, то он квадрат. Доказательство. Исходя из теоремы (если в четырехугольник вписана окружность, то суммы противолежащих сторон равны), AB+CD = BC+AD.
Почему четырехугольник изображенный на рисунке не является квадратом?
Почему четырёхугольник, изображенный на рисунке не является квадратом? Потому что квадрат перевернутый только как ромб!
Как доказать что это квадрат?
Квадрат
- Длины сторон квадрата равны.
- Все углы квадрата прямые.
- Противолежащие стороны квадрата параллельны друг другу.
- Сумма всех углов квадрата равна 360 градусов.
- Величина угла между диагональю и стороной равна 45 градусов.
- Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам.
Как доказать что четырехугольник является прямоугольником?
Если в четырехугольнике все углы равны, то он является прямоугольником. Для этого признака необязательно убеждаться, что перед вами параллелограмм. В любом четырехугольнике сумма углов равна 360. Если все углы равны, то 360/4=90 градусов составляет каждый из углов.
Как доказать что фигура является прямоугольником?
1) Если в параллелограмме все углы равны, то он является прямоугольником. 2) Если в параллелограмме хотя бы один угол прямой, то он является прямоугольником. 3) Если диагонали параллелограмма равны, то он является прямоугольником. 4) Если у четырехугольника три угла прямые, то он является прямоугольником.
Как доказать что четырехугольник выпуклый?
Четырехугольник называется выпуклым, если он находится в одной полуплоскости относительно прямой, содержащей любую его сторону. В школьном курсе рассматриваются только выпуклые четырехугольники. Поэтому далее “выпуклый четырехугольник” будем сокращенно называть “четырехугольник”.
Как доказать что эта фигура параллелограмм?
Четырехугольник является параллелограммом, если:
- Две его противоположные стороны равны и параллельны.
- Противоположные стороны попарно равны.
- Противоположные углы попарно равны.
- Диагонали точкой пересечения делятся пополам.
Как доказать что Авсд параллелограмм?
Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник – параллелограмм. Рассмотрим четырёхугольник ABCD, в котором стороны попарно равны, проведем в нём диагональ AC. Доказательство: Треугольники ABC и ADC равны по трём сторонам.
Что такой параллелограмм?
Параллелогра́мм (др. -греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Как доказать равенство треугольников в параллелограмме?
4) Четырехугольник — параллелограмм, если у него противоположные стороны попарно равны. Чтобы воспользоваться этим признаком параллелограмма, нужно предварительно доказать, что AD=BC и AB=CD. Для этого доказываем равенство треугольников ABC и CDA или BCD и DAB.
Как доказать что треугольники равны по первому признаку?
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Доказательство: Доказывается наложением одного из треугольников на другой. Треугольники полностью совместятся, следовательно, по определению они равны.
Как доказать что это равнобедренный треугольник?
Подытожим:
- Если треугольник равнобедренный, то углы при основании равны, и высота, биссектриса и медиана, проведенные к основанию, совпадают;
- Если в каком-то треугольнике найдутся два равных угла, или какие-то две из трех линий (биссектриса, медиана, высота) совпадут, то такой треугольник – равнобедренный.
Как найти все углы параллелограмма?
Параллелограмм представляет собой четырехугольник, противоположные стороны которого параллельны и равны друг другу. Два угла, прилежащие к одной стороне параллелограмма, в сумме составляют 180°. Если известен один угол параллелограмма, несложно найти смежный с ним угол путем вычитания из 180° величину известного угла.
Как найти все стороны параллелограмма?
Зная диагонали параллелограмма и одну его сторону, можно найти вторую сторону. Для этого нужно извлечь квадратный корень из половины суммы квадратов диагоналей без удвоенного квадрата известной стороны.
Как найти диагональ параллелограмма зная его стороны?
Диагонали параллелограмма
- Формулы диагоналей параллелограмма через стороны и косинус угла β (по теореме косинусов) d1 = √a2 + b2 — 2ab·cosβ
- Формулы диагоналей параллелограмма через стороны и косинус угла α (по теореме косинусов)
- Формула диагонали параллелограмма через две стороны и известную другую диагональ:
Как найти угол между диагоналями параллелограмма?
Диагонали параллелограмма точкой пересечения делятся пополам, откуда AO = OC = AB = CD. Поскольку OC = CD, треугольник COD — равнобедренный, следовательно, ∠COD = ∠CDO = (180° − ∠ACD)/2 = 117°/2 = 58,5°. Угол COD является искомым углом между диагоналями параллелограмма.

