Загрузить PDF
Загрузить PDF
Нахождение числа диагоналей является важнейшим навыком, который пригодится при решении геометрических задач. Это не так сложно, как кажется – просто нужно запомнить формулу. Диагональ – это отрезок, соединяющий любые две несмежные вершины многоугольника.[1]
Многоугольник – это любая фигура с как минимум тремя сторонами. При помощи несложной формулы можно найти количество диагоналей в любом многоугольнике, например, с 4 сторонами или с 4000 сторон.
-
1
Запомните названия многоугольников. Сначала нужно найти число сторон многоугольника. Это можно сделать по названию любого многоугольника. Вот названия самых распространенных многоугольников:[2]
- Четырехугольник: 4 стороны
- Пятиугольник: 5 сторон
- Шестиугольник: 6 сторон
- Семиугольник: 7 сторон
- Восьмиугольник: 8 сторон
- Девятиугольник: 9 сторон
- Десятиугольник: 10 сторон
- Обратите внимание, что у треугольника диагоналей нет.[3]
-
2
Нарисуйте многоугольник. Чтобы найти число диагоналей в квадрате, нарисуйте его. Самый простой способ найти число диагоналей – это нарисовать правильный многоугольник (в таком многоугольнике все стороны равны) и посчитать количество диагоналей. Запомните: неправильный многоугольник будет иметь такое же количество диагоналей, что и правильный (при одинаковом числе сторон).[4]
- Чтобы нарисовать многоугольник, воспользуйтесь линейкой; нарисуйте замкнутую фигуру со сторонами одинаковой длины.
- Если вы не знаете, как выглядит многоугольник, поищите картинки в интернете. Например, знак «Стоп» – это восьмиугольник.
-
3
Нарисуйте диагонали. Диагональ – это отрезок, соединяющий любые две несмежные вершины многоугольника.[5]
Из одной (любой) вершины многоугольника проведите диагонали к другим (несмежным) вершинам.- В квадрате проведите одну диагональ из нижнего левого угла в правый верхний угол, а вторую – из нижнего правого угла в левый верхний угол.
- Нарисуйте диагонали разных цветов, чтобы быстрее посчитать их.[6]
- Обратите внимание, что применять этот метод к многоугольникам, у которых больше 10 сторон, довольно сложно.
-
4
Посчитайте диагонали. Можно считать диагонали во время того, как вы рисуете их, или после того, как они нарисованы. Отмечайте диагонали, которые уже посчитаны, чтобы не запутаться (особенно когда диагоналей много и они пересекаются).
- У квадрата всего две диагонали – по одной на каждые две вершины.[7]
- У шестиугольника 9 диагоналей: по три диагонали на каждые три вершины.
- У семиугольника 14 диагоналей. Если у многоугольника больше семи сторон, посчитать диагонали довольно сложно, потому что их слишком много.
- У квадрата всего две диагонали – по одной на каждые две вершины.[7]
-
5
Каждую диагональ считайте только один раз. Из каждой вершины выходит несколько диагоналей, но это не значит, что число диагоналей равно произведению числа вершин на число диагоналей, выходящих из каждой вершины. Поэтому аккуратно считайте диагонали.[8]
- Например, у пятиугольника (5 сторон) только 5 диагоналей. Из каждой вершины выходит 2 диагонали; если умножить число вершин на число диагоналей, выходящих из каждой вершины, получите 10. Это неверный ответ, как если бы вы посчитали каждую диагональ дважды.
-
6
Попрактикуйтесь в определении числа диагоналей на некоторых примерах. Нарисуйте разные многоугольники и посчитайте их диагонали. Этот метод применим и к неправильным многоугольникам. В случае вогнутого многоугольника некоторые диагонали лежат вне границ фигуры.[9]
- У шестиугольника 9 диагоналей.
- У семиугольника 14 диагоналей.
Реклама
-
1
Запишите формулу. Формула для вычисления числа диагоналей многоугольника: d = n(n-3)/2, где d – число диагоналей, n – число сторон многоугольника.[10]
Используя распределительное свойство, эту формулу можно записать так: d = (n2 – 3n)/2. Можно пользоваться любой формой представленной формулы.- Эта формула для вычисления числа диагоналей многоугольника.
- Обратите внимание, что эта формула не применима к треугольникам, потому что у треугольников диагоналей нет.[11]
-
2
Определите число сторон многоугольника. Чтобы использовать приведенную формулу, нужно знать число сторон многоугольника. Число сторон можно выяснить по названию многоугольника. Ниже приведены части названий многоугольников.[12]
- Четырех (4), пяти (5), шести (6), семи (7), восьми (8), девяти (9), десяти (10), одиннадцати (11), двенадцати (12), тринадцати (13 ), четырнадцати (14), пятнадцати (15) и так далее.
- Если сторон слишком много, то в название многоугольника включается цифра. Например, если у многоугольника 44 стороны, он называется 44-угольником.
- Если дан рисунок многоугольника, просто посчитайте его стороны.
-
3
Подставьте число сторон в формулу. Сделайте это после того, как найдете число сторон многоугольника. Число сторон подставьте вместо n.[13]
- Например. У двенадцатиугольника 12 сторон.
- Запишите формулу: d = n(n-3)/2
- Подставьте число сторон: d = (12(12 – 3))/2
-
4
Решите уравнение. Для этого не забудьте про определенный порядок выполнения математических операций. Начните с вычитания, затем умножьте, а потом разделите. В итоге вы получите число диагоналей многоугольника.[14]
- Например: (12(12 – 3))/2
- Вычитание: (12*9)/2
- Умножение: (108)/2
- Деление: 54
- У двенадцатиугольника 54 диагонали.
-
5
Попрактикуйтесь на других примерах. Чем больше задач вы решите, тем лучше уясните процесс вычисления. Также вы наверняка запомните формулу для вычисления числа диагоналей, что пригодится на экзамене. Не забывайте, что представленная формула применима к многоугольнику, у которого больше трех сторон.
- Шестиугольник (6 сторон): d = n(n-3)/2 = 6(6-3)/2 = 6*3/2 = 18/2 = 9 диагоналей.
- Десятиугольник (10 сторон): d = n(n-3)/2 = 10(10-3)/2 = 10*7/2 = 70/2 = 35 диагоналей.
- Двадцатиугольник (20 сторон): d = n(n-3)/2 = 20(20-3)/2 = 20*17/2 = 340/2 = 170 диагоналей.
- 96-угольник (96 сторон): 96(96-3)/2 = 96*93/2 = 8928/2 = 4464 диагоналей.
Реклама
Об этой статье
Эту страницу просматривали 176 260 раз.
Была ли эта статья полезной?
Семиугольник, виды, свойства и формулы.
Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник, выпуклый и невыпуклый семиугольник
Правильный семиугольник (понятие и определение)
Свойства правильного семиугольника
Формулы правильного семиугольника
Семиугольник в природе, технике и культуре
Шестиугольник, семиугольник, восьмиугольник
Семиугольник, выпуклый и невыпуклый семиугольник:
Семиугольник – это многоугольник с семью углами.
Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый семиугольник – это семиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Звёздчатый семиугольник – семиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого семиугольника могут пересекаться между собой.
Рис. 1. Выпуклый семиугольник
Рис. 2. Невыпуклый семиугольник
Сумма внутренних углов любого выпуклого семиугольника равна 900°.
Правильный семиугольник (понятие и определение):
Правильный семиугольник – это правильный многоугольник с семью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный семиугольник – это семиугольник, у которого все стороны равны, а все внутренние углы равны 128 4/7° ≈ 128,571°.
Рис. 3. Правильный семиугольник
Правильный семиугольник имеет 7 сторон, 7 углов и 7 вершин.
Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный семиугольник невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).
Свойства правильного семиугольника:
1. Все стороны правильного семиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6 = a7.
2. Все углы равны между собой и составляют 128 4/7° ≈ 128,571°.
α1 = α2 = α3 = α4 = α5 = α6 = α7 = 128 4/7° ≈ 128,571°.
Рис. 4. Правильный семиугольник
3. Сумма внутренних углов любого правильного семиугольника равна 900°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного семиугольника O.
Рис. 5. Правильный семиугольник
5. Количество диагоналей правильного семиугольника равно 14.
Рис. 6. Правильный семиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный семиугольник
Формулы правильного семиугольника:
Пусть a – сторона семиугольника, r – радиус окружности, вписанной в семиугольник, R – радиус описанной окружности семиугольника, P – периметр семиугольника, S – площадь семиугольника.
Формулы стороны правильного семиугольника:
Формулы периметра правильного семиугольника:
Формулы площади правильного семиугольника:
Формулы радиуса окружности, вписанной в правильный семиугольник:
Семиугольник в природе, технике и культуре:
В некоторых странах, например, в Великобритании, некоторые монеты имеют правильную криволинейную семиугольную форму.
Некоторые виды кактусовых имеют форму звездчатого семиугольника.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Восьмиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
2 385
I’ve decided to build an object out of building material with straight sides. I have 7 units of the building material, to be arranged on a flat surface, and they are all of the same length. I intend to organize them in a heptagon, which is easy enough when it doesn’t need to be a regular heptagon, as I can just connect the end of one to the next until I reach the last which is then connected to the free end of the first. But now that I have a ‘ring’ of them, and they certainly form a heptagon, I’m struggling to find a way to make sure the heptagon is a regular one, other than just ‘eye-balling it”. My intuition, and my limited recollection of high-school geometry from a couple decades or so ago, tells me that using the length of the diagonals as guides would serve this purpose perfectly. Unfortunately I don’t recall how to determine that length (if, indeed, I ever knew it for heptagons, specifically).
I understand that, for a heptagon, there are 4 diagonals from any one vertex, 2 pairs of 2 different lengths. I suspect finding the length of the shorter of the two would be the most useful to my situation, but a way to find either one, or both, would be appreciated.
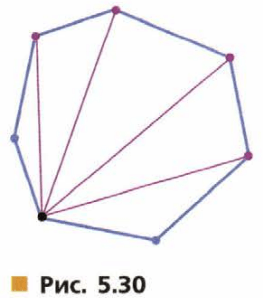
Число диагоналей многоугольника (рис.5.30) можно подсчитать так:
найти число диагоналей, выходящих из одной вершины, − их на 3 меньше, чем вершин;
умножить это число на число вершин;
разделить результат на 2 (объясните почему).
Сколько диагоналей у семиугольника, десятиугольника, стоугольника?
reshalka.com
Математика 5 класс Дорофеев. 5.3 Ломаные и многоугольники. Номер №413
Решение
Разделить на 2 нужно для того, чтобы не учитывать одни и те же диагонали, которые выходят как из одного угла в другой, так и из другого угла в первый.
(7 − 3) * 7 : 2 = 4 * 7 : 2 = 28 : 2 = 14 (диагоналей) − у семиугольника;
(10 − 3) * 10 : 2 = 7 * 10 : 2 = 70 : 2 = 35 (диагоналей) − у десятиугольника;
(100 − 3) * 100 : 2 = 97 * 100 : 2 = 9700 : 2 = 4850 (диагоналей) − у стоугольника.
Сколько диагоналей в семиугольнике?
7 14
Сколько диагоналей в восьмиугольнике?
20 диагоналей ∴ Восьмиугольник имеет 20 диагоналей. Следовательно, вариант С является правильным ответом. Примечание: Восьмиугольник — это многоугольник в геометрии, который имеет 8 сторон и 8 углов.
См. также, что означает поверхность
Как найти диагональ правильного семиугольника?
Следовательно, длина диагонали будет 2 * х то есть 1,802 * а.
Сколько сторон у семиугольника?
Семь
В геометрии семиугольник или септагон — это многоугольник с семью сторонами или 7-угольник.
Сколько диагоналей в пятиугольнике?
пять многоугольников: сколько диагоналей? (Для пар или групп учащихся) Диагональ правильного многоугольника – это прямая линия, соединяющая две несмежные вершины. Таким образом, у квадрата две диагонали, а у правильного пятиугольника пять, как показано ниже.
Почему у семиугольника 14 диагоналей?
Семиугольник – определение с примерами
Гептагон — это многоугольник (замкнутая фигура, состоящая из отрезков прямой), состоящий из 7 сторон и 7 углов. … В семиугольнике 14 диагоналей, и в данном семиугольнике синие отрезки представляют собой диагонали.
Сколько диагоналей в выпуклом семиугольнике?
14 диагоналей. Семиугольник имеет 14 диагоналей.
Сколько вершин в семиугольнике?
7
Какова мера семиугольника?
Свойства семиугольника
Сумма всех внутренних углов равна 900°. Сумма внешних углов равна 360°. Правильный семиугольник имеет все семь сторон одинаковой длины. Каждый внутренний угол правильного семиугольника равен 128,571°.
Сколько градусов в семиугольнике?
900°
Сколько диагоналей может иметь семиугольник, на котором можно нарисовать подходящую фигуру, подтверждающую ваш ответ?
Классификация полигонов
| Имя полигона | Количество сторон | Количество диагоналей |
|---|---|---|
| четырехугольник | 4 | 2 |
| Пентагон | 5 | 5 |
| Шестиугольник | 6 | 9 |
| Семиугольник | 7 | 14 |
Какой многоугольник имеет 35 диагоналей?
десятиугольник Многоугольник с 10 сторонами называется десятиугольник. ∴ Декагон имеет 35 диагоналей.
Как найти диагонали?
Вы можете найти диагональ прямоугольника, если у вас есть ширина и высота. То диагональ равна квадратному корню из квадрата ширины плюс квадрат высоты.
Как выглядит семиугольник?
Форма семиугольника представляет собой плоскость или двумерную форму, состоящую из семь прямых сторон, семь внутренних углов и семь вершин. Форма семиугольника может быть правильной, неправильной, вогнутой или выпуклой. … Все семиугольники можно разделить на пять треугольников. Все семиугольники имеют 14 диагоналей (отрезков, соединяющих вершины).
Смотрите также, почему американский школьный обед такой плохой
Какой многоугольник является семиугольником?
семиугольник – это многоугольник с семью сторонами. Это замкнутая фигура, имеющая 7 вершин. Семиугольник также иногда называют Септагоном.
…
| Ссылки по теме | |
|---|---|
| Треугольник | Круг |
| Октагон | Квадратный |
Является ли семиугольник вогнутым или выпуклым?
Если один или несколько внутренних углов больше 180 °, он вогнутый. Правильный семиугольник – это выпуклый семиугольник. Вогнутый семиугольник – это неправильный семиугольник.
…
Классификация семиугольников.
| Правильный семиугольник | Неправильный семиугольник |
|---|---|
| Все стороны и внутренние углы равны | Не все стороны и углы равны |
Сколько треугольников в семиугольнике?
четырнадцать конгруэнтных Правильный семиугольник (с красными сторонами), его более длинные диагонали (зеленые) и его более короткие диагонали (синие). Каждый из четырнадцать конгруэнтные семиугольные треугольники имеют одну зеленую сторону, одну синюю сторону и одну красную сторону.
Сколько диагоналей у Тридекагона?
Классификация полигонов
| Имя | Количество сторон | Количество диагоналей |
|---|---|---|
| десятиугольник | 10 | 35 |
| Хендекагон | 11 | 44 |
| додекагон | 12 | 54 |
| Тридекагон | 13 | 65 |
Как нарисовать семиугольник?
Сколько диагоналей можно провести из одной вершины семиугольника?
Диагонали образованы всеми точками, кроме соседних сторон. Из нарисованной выше диаграммы мы можем сказать, что из одной вершины семиугольника мы можем провести только 4 диагонали.
Как называется семигранник?
семиугольник представляет собой многоугольник с семью сторонами. Его также иногда называют септагоном, хотя это использование смешивает латинский префикс sept- (производный от septua-, что означает «семь») с греческим суффиксом -gon (от gonia, что означает «угол»), и поэтому не рекомендуется.
Что такое вершина семиугольника?
Семиугольник имеет семь вершин. Семиугольник – это многоугольник с семью сторонами. Вершины семиугольника точки, в которых стороны семиугольника…
Сколько осей симметрии у семиугольника?
7
Как найти угол семиугольника?
Как найти площадь семиугольника?
Определение площади семиугольника
Формула для этого Площадь = (1/2) нср. В данном случае «n» — количество сторон, «s» — длина сторон, «r» — апофема. Используя тот же пример выше, со стороной 7, формула площади будет работать следующим образом: Площадь = (1/2) (7) (7) (7,268).
См. также, кто был на вершине структуры социального класса в обществе инков?
Что означает септагон?
Фильтры. (запрещено) Многоугольник с семью сторонами и семью углами; семиугольник. имя существительное.
Чему равен один внешний угол семиугольника?
51.43∘ 51.43∘ является мерой каждого внешнего угла в правильном семиугольнике.
У какого многоугольника 12 сторон?
додекагон
| Правильный додекагон | |
|---|---|
| Правильный двенадцатиугольник | |
| Тип | Правильный многоугольник |
| Ребра и вершины | 12 |
| Символ Шлефли | {12}, т{6}, т{3} |
Как называется многоугольник с 29 сторонами?
Как называется многоугольник с…?
| # | Имя многоугольника + геометрический рисунок |
|---|---|
| 27 сторон | семикосагон |
| 28 сторон | восьмиугольник |
| 29 сторон | эннеаикосагон |
| 30 сторон | триаконтагон |
Сколько диагоналей у 50-стороннего многоугольника?
Количество диагоналей в многоугольнике с 50 сторонами равно 1175.
Какова диагональ квадрата 12×12?
17″ Нахождение диагонали квадрата
| Квадратный размер | Диагональ |
|---|---|
| 12″ | 17″ |
| 12 1/2″ | 17 5/8″ |
| 13″ | 18 3/8″ |
| 13 1/2″ | 19 1/8″ |
Сколько диагоналей в окружности?
Круг имеет бесконечное число диаметра и хорд, соединяющих бесконечные вершины. И диаметры, и хорды являются диагоналями многоугольников с бесконечным числом вершин. Следовательно, круг имеет бесконечное число диагоналей.
Сколько диагоналей в многоугольнике с 15 сторонами?
Следовательно, есть 90 диагоналей в 15-стороннем многоугольнике.