Диагонали трапеции взаимно перпендикулярны как найти площадь – Сайт, где вы сможете решить свои вопросы

Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.

1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.

v-ravnobedrennoj-trapecii-diagonali-perpendikulyarny

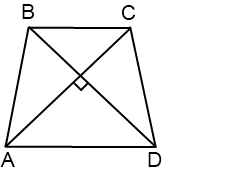
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.

diagonali-ravnobokoj-trapecii-perpendikulyarny

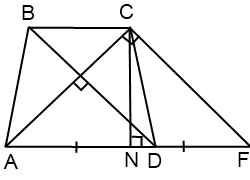
Четырехугольник BCFD — параллелограмм ( BC∥DF как основания трапеции, BD∥CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.

Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то

$[CN = frac{1}{2}AF = frac{{AD + BC}}{2},]$

что в общем виде можно записать как

$[h = frac{{a + b}}{2},]$

где h — высота трапеции, a и b — ее основания.

2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.

Так как средняя линия трапеции m равна полусумме оснований, то

3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).

Так как площадь трапеции находится по формуле

$[S = frac{{a + b}}{2} cdot h]$

а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:

$[h = frac{{a + b}}{2} = m,]$

то

$[S = {h^2}]$

$[S = {(frac{{a + b}}{2})^2}]$

$[S = {m^2}.]$

4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.

Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле

$[S = frac{1}{2}{d_1}{d_2}sin varphi ]$

sin 90º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна

$[S = frac{1}{2}{d^2}.]$

откуда

$[frac{1}{2}{d^2} = {(frac{{a + b}}{2})^2} = {h^2} = {m^2},]$

$[{d^2} = frac{{{{(a + b)}^2}}}{2}.]$

Источник

Площадь равнобедренной трапеции можно найти с помощью любой из формул для нахождения площади трапеции в общем случае. Благодаря свойствам равнобедренной трапеции некоторые из этих формул могут быть упрощены.

I Площадь трапеции равна произведению полусуммы оснований на высоту.

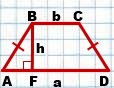ploshchad-ravnobedrennoj-trapecii Как и для случая произвольной трапеции, площадь равнобедренной трапеции ABCD, AD∥BC, AB=CD,

$[{S_{ABCD}} = frac{{AD + BC}}{2} cdot BF]$

Если AD=a, BC=b, BF=h, то формула площади трапеции принимает вид

$[S = frac{{a + b}}{2} cdot h]$

II. Площадь трапеции равна произведению её средней линии на высоту.

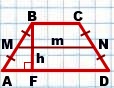formula-ploshchadi-ravnobedrennoj-trapecii Это верно, в частности, для равнобедренной трапеции.

Если MN — средняя линия трапеции ABCD, BF — её высота, то площадь трапеции равна

$[{S_{ABCD}} = MN cdot BF]$

Если MN=m, BF=h, то

III. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.

Поскольку диагонали равнобедренной трапеции равны, площадь равнобедренной трапеции равна половине произведения квадрата её диагонали на синус угла между диагоналями.

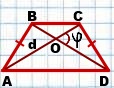ploshchad-ravnobedrennoj-trapecii-cherez-diagonali Для равнобедренной трапеции ABCD

AD∥BC, AB=CD, AC∩BD=O,

$[{S_{ABCD}} = frac{1}{2}A{C^2} cdot sin angle COD]$

Если AC=d, ∠COD=φ

$[S = frac{1}{2}{d^2}sin varphi ]$

VI. Площадь равнобедренной трапеции с перпендикулярными диагоналями.

1) Если диагонали равнобедренной трапеции перпендикулярны, так как sin 90º=1, предыдущая формула принимает вид:

$[S = frac{1}{2}{d^2}]$

2) Площадь равнобедренной трапеции, диагонали которой перпендикулярна, равна квадрату её высоты.

ploshchad-ravnobedrennoj-trapecii-diagonali-perpendikulyarny В равнобедренной трапеции ABCD

AD∥BC, AB=CD, AC∩BD=O, проведем высоту FK через точку пересечения диагоналей.

Прямоугольные треугольники AOD и BOC — равнобедренные (с основаниями AD и BC). Поэтому их высоты OK и OF являются также медианами. Следовательно, по свойству медианы, проведенной к гипотенузе

$[OK = frac{1}{2}AD,OF = frac{1}{2}BC.]$

$[{S_{ABCD}} = frac{{AD + BC}}{2} cdot FK = ]$

$[ = (frac{{AD}}{2} + frac{{BC}}{2}) cdot FK = ]$

$[ = (OK + OF) cdot FK = FK cdot FK = F{K^2}.]$

Таким образом, формула для нахождения площади равнобедренной трапеции с перпендикулярными диагоналями:

$[S = {h^2}]$

V. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

ploshchad-ravnobedrennoj-trapecii-cherez-radius

Так как в трапецию ABCD можно вписать окружность, то

AD+BC=AB+CD, то есть p=AD+BC или p=AB+CD=2AB.

Таким образом, площадь равнобедренной трапеции, в которую можно вписать окружность, равна произведению суммы оснований на радиус окружности.

Если обозначить основания трапеции AD=a, BC=b, то

Также площадь равнобедренной трапеции, в которую можно вписать окружность, равна удвоенному произведению боковой стороны на радиус окружности.

Если обозначить боковые стороны AB=CD=c, то формула площади трапеции в этом случае

Так как высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями, то площадь равнобедренной трапеции, в которую можно вписать окружность, равна произведению среднего арифметического и среднего геометрического её оснований:

$[S = frac{{a + b}}{2} cdot sqrt {ab} ]$

Источник

Светило науки – 29155 ответов – 105369 раз оказано помощи

Ответ: 100 .

Трапеция АВСД , АВ=СД , высота h=10 , АС⊥ВД . Найти S .

Проведём высоту НР через точку О – точку пересечения диагоналей трапеции. Обозначим основания а=АД , b=ВС .

Рассм. ΔАСД и ΔАВД . Они равны, так как АД – общая сторона , АВ=СД по условию, ∠А=∠Д , как углы при основании равнобокой трапеции.

Из равенства треугольников следует равенство ∠САД=∠ВДА ⇒ ΔАОД – равнобедренный и АО=ОД . К тому же в этом тр-ке ∠АОД=90° . Значит высота ОН является и медианой , АН=НД=a/2 .

Но медиана, проведённая из прямого угла на гипотенузу, равна половине гипотенузы , ОН=1/2*АВ=a/2 .

Так как АО=ОД и в равнобокой трапеции диагонали равны АС=ВД , то и ВО=СО ( так как ВО=ВД-ОД=АС-ОA=ОС ) ⇒ ΔВОС тоже равнобедренный и прямоугольный. И его высота ОР явл. медианой , аналогично получаем, что ОР=ВО=ОС=b/2 .

Тогда высота трапеции равна .

Запишем, чему равна площадь трапеции .

P.S. Попутно доказано, что в равнобокой трапеции , у которой перпендикулярны диагонали, высота трапеции равна полусумме оснований ( средней линии) , и площадь такой трапеции равна квадрату высоты .