Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком “минус”:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй – пять третьих и от четвертой – три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ – определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки –
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
Определитель матрицы
Определителем
квадратной матрицы
называется число, которое обозначается
какили
и вычисляется при помощи следующих трех
правил.
Правило
1.
Определитель диагональной матрицы
равен произведению элементов, стоящих
на главной диагонали.
Замечание:
Определитель одноэлементной матрицы
равен самому элементу.
Правило
2.
Общий множитель элементов любой строки
или столбца матрицы можно вынести за
знак определителя.
Замечание:
Определитель матрицы, у которой строка
или столбец состоит только из нулей,
равен
.
Правило
3.
Определитель матрицы не изменится, если
к одной из строк (столбцов) матрицы
прибавить другую строку (столбец) этой
матрицы.
Свойства определителя матрицы.
1.
Определитель не меняется при
транспонировании.
2. Если
в определителе переставить две строки,
определитель поменяет знак.
3.
Определитель, содержащий две одинаковые
строки, равен нулю.
4.
Определитель, содержащий две
пропорциональные строки, равен нулю.
5. Если
все элементы
строки определителя представлены в
виде суммы двух слагаемых,
то определитель равен сумме определителей,
у которых все строки, кроме,
– такие же, как в заданном определителе,
астрока в одном из слагаемых состоит из
элементов,
в другом – из элементов.
Замечание.
Все свойства остаются справедливыми,
если вместо строк взять столбцы.
Миноры и алгебраические дополнения
Обозначим
через
матрицу, которая остается при вычеркивании
из матрицыстроки и
столбца. Тогда
называется минором элемента
.
Величинаназывается алгебраическим дополнением
элемента.
Разложение определителя матрицы по элементам строки или столбца.
Теорема.
Определитель каждой матрицы равен сумме
произведений элементов любой ее строки
(столбца) на их алгебраические дополнения,
т. е. при разложении по элементам
строки
Для
вычисления значений определителей
матриц второго порядка пользуются
формулой:
Для
вычисления значений определителей
матриц третьего порядка можно
воспользоваться формулой разложения
определителя по первой строке:
Пример
7.
Не
вычисляя определителя

показать, что он равен нулю.
Решение.
Вычтем
из второй строки первую, получим
определитель

равный исходному. Если из третьей
строки также вычесть первую, то получится
определитель

в котором две строки пропорциональны.
Такой определитель равен нулю.
Пример
8.
Вычислить
определитель

разложив его по элементам второго
столбца.
Решение.
Разложим
определитель по элементам второго
столбца:
4. Ранг матрицы
Рассмотрим
прямоугольную матрицу
.
Если в этой матрице выделить произвольнострок и
столбцов, то элементы, стоящие на
пересечении выделенных строк и столбцов,
образуют квадратную матрицупорядка. Определитель этой матрицы
называетсяминором
k-го порядка матрицы
.
Очевидно, что матрицаобладает минорами любого порядка от
до наименьшего из чисел
и
.
Некоторые среди них будут равны нулю.
Среди всех отличных от нуля миноров
матрицынайдется, по крайней мере, один минор,
порядок которого будет наибольшим.
Наибольший из порядков миноров данной
матрицы, отличных от нуля, называется
рангом
матрицы. Если ранг
матрицы
равен
,
то это означает, что в матрицеимеется отличный от нуля минор порядка
,
но всякий минор порядка, большего чем,
равен нулю. Ранг матрицыобозначается через
.
Очевидно, что выполняется соотношение
Ранг
матрицы находится либо методом окаймления
миноров, либо методом элементарных
преобразований. При вычислении ранга
матрицы первым способом следует
переходить от миноров низших порядков
к минорам более высокого порядка. Если
уже найден минор
порядка матрицы
,
отличный от нуля, то требуют вычисления
лишь минорыпорядка, окаймляющие минор
,
т.е. содержащие его в качестве минора.
Если все они равны нулю, то ранг матрицы
равен.
Элементарными
называются следующие преобразования
матрицы:
-
перестановка
двух любых строк (или столбцов), -
умножение
строки (или столбца) на отличное от нуля
число, -
прибавление
к одной строке (или столбцу) другой
строки (или столбца), умноженной на
некоторое число.
Две
матрицы называются
эквивалентными,
если одна из них получается из другой
с помощью конечного множества элементарных
преобразований.
Эквивалентные
матрицы не являются, вообще говоря,
равными, но их ранги равны. Если матрицы
и
эквивалентны, то это записывается так:
.
Каноническойматрицей называется матрица, у которой
в начале главной диагонали стоят подряд
несколько единиц (число которых может
равняться нулю), а все остальные элементы
равны нулю, например,

При
помощи элементарных преобразований
строк и столбцов любую матрицу можно
привести к канонической. Ранг канонической
матрицы равен числу единиц на ее главной
диагонали.
Пример
11.
Найти методом окаймления миноров ранг
матрицы
Решение.
Начинаем
с миноров
порядка, (т.е. с элементов матрицы
).
Выберем, например, минор (элемент),
расположенный в первой строке и первом
столбце. Окаймляя при помощи второй
строки и третьего столбца, получаем
минор,
отличный от нуля. Переходим теперь к
минорампорядка, окаймляющим
.
Их всего два (можно добавить второй
столбец или четвертый). Вычисляем их:

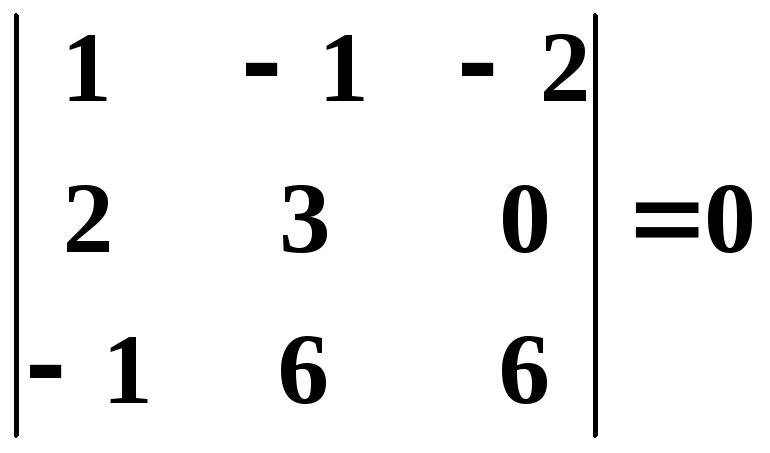
Таким
образом, все окаймляющие миноры третьего
порядка оказались равными нулю. Ранг
матрицы
равен двум.
Пример
12.
Найти ранг матрицы
и
привести ее к каноническому виду.
Решение. Из второй строки
вычтем первую и переставим эти строки:

Теперь из второй и третьей
строк вычтем первую, умноженную
соответственно на
и
:

из третьей строки вычтем
вторую, при этом получим матрицу

которая эквивалентна матрице
,
так как получена из нее с помощью
конечного множества элементарных
преобразований. Очевидно, что ранг
матрицыравен
,
а следовательно, и.
Матрицу
легко привести к канонической.
Вычитая первый столбец,
умноженный на подходящие числа, из всех
последующих, обратим в нуль все элементы
первой строки, кроме первого, причем
элементы остальных строк не изменяются.
Затем, вычитая второй
столбец, умноженный на подходящие числа,
из всех последующих, обратим в нуль все
элементы второй строки, кроме второго,
и получим каноническую матрицу:
.
Соседние файлы в папке Лекц.Мат-ка Базов
- #
- #
- #
- #
- #
- #
Диагональная матрица — квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю:
.
Диагональная матрица 


Является одновременно и верхнетреугольной и нижнетреугольной. Диагональная матрица симметрична: 
Диагональные матрицы можно складывать и перемножать почленно:


Определитель диагональной матрицы равен произведению диагональных элементов: 
Алгебраическое дополнение недиагонального элемента диагональной матрицы равно нулю, то есть:
.
Обратная матрица для диагональной матрицы равна:
.
Диагональными являются нулевая матрица, единичная матрица, скалярная матрица (все элементы главной диагонали равны).
В некоторых случаях недиагональная матрица может быть приведена к диагональному виду путём замены базиса; достаточным условием является различность всех собственных значений матрицы (в общем случае матрица приводима лишь к жордановой форме).
A matrix is defined as a rectangular array of numbers that are arranged in rows and columns. The size of a matrix can be determined by the number of rows and columns in it. A matrix is said to be an “m by n” matrix when it has “m” rows and “n” columns and is written as an “m × n” matrix. For example, the order of the matrix that has five rows and four columns is “5 × 4.” We have different types of matrices, such as rectangular, square, triangular, symmetric, singular, etc. The image given below is an “m × n” matrix that has “m” rows and “n” columns.
What is a Diagonal Matrix?
A diagonal matrix is a square matrix in which all of the elements except the principal diagonal elements are zeroes. It is both upper and lower triangular, as all the elements except the main diagonal elements are zeros. A square matrix “A = [aij]” is said to be a diagonal matrix if aij = 0 when i ≠ j. The matrix given below represents a diagonal matrix of order “5 × 5.”
Examples of a Diagonal Matrix
Some common examples of diagonal matrices of different orders are given below:
- Diagonal Matrix of order (3 × 3)
- Diagonal Matrix of order (4 × 4)
Properties of a Diagonal Matrix
The following are the properties of the Singular Matrix:
- Every diagonal matrix is a square matrix, i.e., a matrix that has an equal number of rows and columns.
- Scalar matrices, identity matrices, and null matrices are examples of diagonal matrices, as their non-principal diagonal elements are zeros.
- The resultant matrix of the sum of two diagonal matrices is also a diagonal matrix.
- The resultant matrix of the product of diagonal matrices is also a diagonal matrix, where the main diagonal elements of the resultant matrix are products of the corresponding elements of the original matrices.
If
and
, then
.
- A diagonal matrix is a symmetric matrix, as the transpose of a diagonal matrix is the same matrix itself.
If
is a diagonal matrix, then
, i.e., D = DT.
- A diagonal matrix is a symmetric matrix, as the transpose of a diagonal matrix is the same matrix itself.
If
and
are two diagonal matrices, then
Block Diagonal Matrix
The term “block matrix” refers to a matrix that is divided into blocks. In such matrices, the non-diagonal blocks are zero matrices, whereas the main diagonal blocks are square matrices. A matrix “A = [aij]” is called a block diagonal matrix when aij = 0, for i ≠ j, i.e., when the non-diagonal blocks are zero.
Determinant of a Diagonal Matrix
The determinant of a diagonal matrix is equal to the product of its principal diagonal elements.
If,
|D| = a11 × a22 × a33.
Inverse of a Diagonal Matrix
The inverse of a diagonal matrix is also a diagonal matrix with the principal diagonal’s elements being the reciprocals of the corresponding elements of the original matrix.
If
, then
.
Anti-Diagonal Matrix
An anti-diagonal matrix, or non-diagonal matrix, is said to be the mirror image of a diagonal matrix concerning the placement of the elements. In an anti-diagonal matrix, all elements are zero except the diagonal (not the principal diagonal) elements from the upper right edge to the lower left edge. The matrix given below is an anti-diagonal matrix of order “3 × 3.”
Also, Check
- Minors and Cofactors of Determinants
- Adjoint of a Matrix
- Determinant of a Matrix
Solved Examples on Diagonal Matrix
Example 1: If ![Rendered by QuickLaTeX.com A = left[begin{array}{ccc} -4 & 0 & 0\ 0 & 11 & 0\ 0 & 0 & 7 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1d31338d51013ce08e9ee33b78ebbea9_l3.png)
Solution:
Given matrix, A =
= A
So, A = AT
Hence proved.
Example 2: Find the determinant of the matrix given below.
Solution:
Given matrix, D =
We can notice that the given matrix is a diagonal matrix. We know that the determinant of a diagonal matrix is equal to the product of its principal diagonal elements.
So, |D| = -5 × 0 × 14 = 0
Hence, the determinant of the given matrix is 0.
Example 3: Find the inverse of the matrix given below.
Solution:
We can notice that the given matrix is a diagonal matrix. We know that the inverse of a diagonal matrix is obtained by replacing the principal diagonal’s elements with the reciprocals of the corresponding elements of the original matrix, while the rest of the elements remain the same.
So,
.
Example 4: Prove that A + B = B + A, if ![Rendered by QuickLaTeX.com A = left[begin{array}{cc} 6 & 0\ 0 & 7 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e8334b95c3eabc20495e66db297ffc84_l3.png)
![Rendered by QuickLaTeX.com B = left[begin{array}{cc} -10 & 0\ 0 & 13 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-34c9438880f8b8412bd41a64a8c60657_l3.png)
Solution:
Given matrices,
So, A + B = B + A
Hence, proved.
FAQs on Diagonal Matrix
Question 1: Define a diagonal matrix.
Answer:
A diagonal matrix is a square matrix in which all of the elements except the principal diagonal elements are zeroes.
Question 2: Is an identity matrix a diagonal matrix?
Answer:
An identity matrix is a square matrix whose principal diagonal elements are ones and the rest of the elements are zeros. So, an identity matrix or unit matrix is a diagonal matrix.
Question 3: What is the determinant of a diagonal matrix?
Answer:
The determinant of a diagonal matrix is equal to the product of its principal diagonal elements.
If
, then |D| = a11 × a22 × a33.
Question 4: Is a zero matrix a diagonal matrix?
Answer:
A diagonal matrix is a square matrix whose non-diagonal elements are zeroes. We know that in a zero matrix all its elements are zeroes. So, we can conclude that a zero matrix is a diagonal matrix.
Last Updated :
09 Jan, 2023
Like Article
Save Article
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое Определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 

Возьмем теперь квадратную матрицу -го порядка
|
|
(9.2) |
Для записи определителя -го порядка матрицы
будем применять обозначения
. При
матрица
состоит из одного элемента и ее определитель равен этому элементу. При
получаем определитель
.
Минором элемента
матрицы
называют определитель матрицы
-го порядка, получаемого из матрицы
вычеркиванием
-той строки и
-го столбца.
Пример 7. Найти минор матрицы:

По определению, минор элемента
есть определитель матрицы, получаемой из матрицы
вычеркиванием первой строки и второго столбца. Следовательно,

Алгебраическим дополнением элемента матрицы
называется минор
, взятый со знаком
. Алгебраическое дополнение элемента
обозначается
, следовательно,
.
Пример 8. Найти алгебраическое дополнение элемента матрицы
из примера 7.

Определителем квадратной матрицы
-го порядка
называется число:
|
|
(9.3) |
Где ‑ элементы первой строки матрицы (9.2), а
их алгебраические дополнения
.
Запись по формуле (9.3) называется Разложением определителя по первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы
-го порядка
называется число:
|
|
(9.4) |
Где ‑ элементы первого столбца матрицы (9.2), а
их алгебраические дополнения
.
Свойство 2. Если поменять местами две строки или два столбца матрицы , то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы -го порядка (будем в дальнейшем говорить определитель
-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
, или
.
Свойство 3. Определитель, у которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе две одинаковые сроки местами. Тогда, по свойству 2 получим определитель
, но с другой стороны, определитель не изменится, т. е.
. Отсюда
.
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя умножить на число
, то определитель умножится на
.
.
Умножим элементы -той строки на
. Тогда получим определитель:
.
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пропорциональны, равен нулю.
Пусть -я строка пропорциональна
-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя есть сумма двух слагаемых, то определитель
равен сумме двух определителей: у одного из них
-той строкой (столбцом)служат первые слагаемые, а у другого – вторые.
Разложив определитель по
-той строке получим:
.
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам -той строки определителя
соответствующие элементы
-ой строки, умноженные на число
, получим определитель
. Определитель
равен сумме двух определителей: первый есть
, а второй равен нулю, так как у него
-тая и
-тая строки пропорциональны.
Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т. е.:
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель , который получается из данного определителя
заменой
-той строки
-той строкой. Определитель
равен нулю, так как у него две одинаковые строки. Разложив его по
-той строке получим:
.
Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т. е. .
| < Предыдущая | Следующая > |
|---|









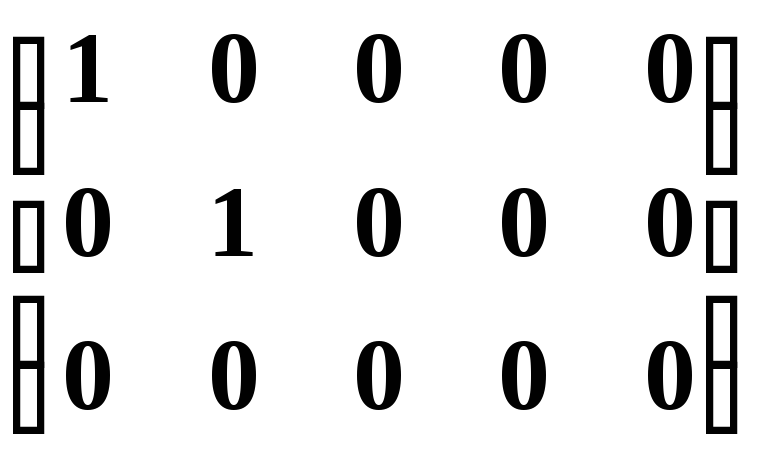






![Rendered by QuickLaTeX.com A = left[begin{array}{cc} -3 & 0\ 0 & -3 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-938e6eeb199d18efe9b6a81c155325c6_l3.png) and
and ![Rendered by QuickLaTeX.com B = left[begin{array}{cc} 8 & 0\ 0 & 5 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-289270571d1376916067677d8c61d425_l3.png) , then
, then ![Rendered by QuickLaTeX.com AB = left[begin{array}{cc} -24 & 0\ 0 & -15 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-548593b5973b5802dca81958f218a318_l3.png) .
.![Rendered by QuickLaTeX.com D = left[begin{array}{cc} 6 & 0\ 0 & 7 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-019923f6d9b5f12ac72dc01f6753cefa_l3.png) is a diagonal matrix, then
is a diagonal matrix, then ![Rendered by QuickLaTeX.com D^{T} = left[begin{array}{cc} 6 & 0\ 0 & 7 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec835ef1f32820843ac3b0f873112e46_l3.png) , i.e., D = DT.
, i.e., D = DT.![Rendered by QuickLaTeX.com A = left[begin{array}{cc} -5 & 0\ 0 & 11 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f7d7c1e2d6631cca2bfeb0f5b8ab3ecb_l3.png) and
and ![Rendered by QuickLaTeX.com B = left[begin{array}{cc} 7 & 0\ 0 & -13 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c1b7ad181af872ae58fedba99bf49c4e_l3.png) are two diagonal matrices, then
are two diagonal matrices, then![Rendered by QuickLaTeX.com A + B = B + A = left[begin{array}{cc} 2 & 0\ 0 & -2 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a91da227fd05345afe8ecb5b7b1cb8f_l3.png)
![Rendered by QuickLaTeX.com AB = BA = left[begin{array}{cc} -35 & 0\ 0 & -143 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fea9a7cdc2724f3bbfc5bdc7de969c32_l3.png)
![Rendered by QuickLaTeX.com A = left[begin{array}{cccccc} a_{11} & 0 & 0 & . & . & 0\ 0 & a_{22} & 0 & . & . & 0\ 0 & 0 & a_{33} & . & . & 0\ . & . & . & . & . & .\ . & . & . & . & . & .\ 0 & 0 & 0 & . & . & a_{nn} end{array}right]_{ntimes n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5699314a56642348fca6bdf4db0ca627_l3.png)
![Rendered by QuickLaTeX.com D = left[begin{array}{ccc} a_{11} & 0 & 0\ 0 & a_{22} & 0\ 0 & 0 & a_{33} end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8243edd7364cb138aff6c0327bc34451_l3.png)
![Rendered by QuickLaTeX.com D = left[begin{array}{ccc} a_{11} & 0 & 0\ 0 & a_{22} & 0\ 0 & 0 & a_{33} end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fb41942966d6aec8c1c35c36fc83e084_l3.png) , then
, then ![Rendered by QuickLaTeX.com D^{-1} = left[begin{array}{ccc} frac{1}{a_{11}} & 0 & 0\ 0 & frac{1}{a_{22}} & 0\ 0 & 0 & frac{1}{a_{33}} end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11be460ddf76fdeda27a56a692b6ae7e_l3.png) .
.![Rendered by QuickLaTeX.com A = left[begin{array}{ccc} 0 & 0 & a_{11}\ 0 & a_{22} & 0\ a_{33} & 0 & 0 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d419dc21ead4c8d4ced74ef3ddf94cbb_l3.png)
![Rendered by QuickLaTeX.com left[begin{array}{ccc} -4 & 0 & 0\ 0 & 11 & 0\ 0 & 0 & 7 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdd8c58937fa53a007dd14163fc8e354_l3.png)
![Rendered by QuickLaTeX.com A^{T} = left[begin{array}{ccc} -4 & 0 & 0\ 0 & 11 & 0\ 0 & 0 & 7 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7d6bfd8cc30e3e49b97b984ca8568157_l3.png) = A
= A![Rendered by QuickLaTeX.com D = left[begin{array}{ccc} -5 & 0 & 0\ 0 & 0 & 0\ 0 & 0 & 14 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-adb6125ba55def67832f3c96582baedb_l3.png)
![Rendered by QuickLaTeX.com left[begin{array}{ccc} -5 & 0 & 0\ 0 & 0 & 0\ 0 & 0 & 14 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72e5f802555283dd8c581f8b065d907b_l3.png)
![Rendered by QuickLaTeX.com B = left[begin{array}{cc} 11 & 0\ 0 & 17 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f126ecd18ff3b744fc6977334597f0ad_l3.png)
![Rendered by QuickLaTeX.com B^{-1} = left[begin{array}{cc} frac{1}{11} & 0\ 0 & frac{1}{17} end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-692b63ab91effdec2179e5f55f52df51_l3.png) .
.![Rendered by QuickLaTeX.com A = left[begin{array}{cc} 6 & 0\ 0 & 7 end{array}right] and B = left[begin{array}{cc} -10 & 0\ 0 & 13 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0bc0143d4f434b0c4d7cc223bc83a6f0_l3.png)
![Rendered by QuickLaTeX.com A + B = left[begin{array}{cc} -4 & 0\ 0 & 20 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8cfd30875d6af172872623bbdcd25b6f_l3.png)
![Rendered by QuickLaTeX.com B + A = left[begin{array}{cc} -4 & 0\ 0 & 20 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-48635b59f77a1a04b0551444672e7da8_l3.png)


