Площадь диагонального сечения параллелепипеда
У прямоугольного параллелепипеда диагональное сечение представляет собой прямоугольник.

Значит, для нахождения его площади нужно воспользоваться формулой площади прямоугольника:
S = a * b.
Сторона a совпадает с диагональю основания параллелепипеда.
Длину диагонали основания можно найти по теореме Пифагора, поскольку данная диагональ разбивает прямоугольник на 2 прямоугольных треугольника и является в каждом из них гипотенузой.
BD² = AB² + AD². => BD = √(AB² + AD²).
Сторона b равна высоте параллелепипеда (боковому ребру).
Высоту параллелепипеда можно, например, найти по его объёму и площади основания.
У прямоугольного параллелепипеда основание – это прямоугольник, поэтому площадь основания равна произведению его длины и ширины (на рисунке это AB и AD).
BB1 = V / (AB * AD).
Далее рассмотрим несколько примеров.
**
Пример 1
Стороны основания прямоугольного параллелепипеда равны 12 см и 4 см, а высота равна 5 см.
Нужно найти площадь диагонального сечения.
S (сеч) = √(12² + 4²) * 5 = √140 * 5 = 2√35 * 5 = 10√35 см.
**
Пример 2
Стороны основания и высота прямоугольного параллелепипеда относятся как 1:2:3, а его объём равен 48 см².
Нужно найти площадь диагонального сечения.
1) Сначала найдём, чему равны стороны основания и высота.
V = abc = 48.
Пусть a = x, b = 2x, c = 3x.
x * 2x * 3x = 48.
6x³ = 48.
x³ = 8.
x = 2.
Таким образом, стороны основания равны 2 и 4 см соответственно, а высота равна 6 см.
2) Теперь всё решается так же, как и в 1 примере.
S (сеч) = √(2² + 4²) * 6 = √20 * 6 = 2√5 * 6 = 12√5 см.
Как найти площадь диагонального сечения
Если по обе стороны некоторой плоскости есть точки, принадлежащие объемной фигуре (например, многограннику), эту плоскость можно назвать секущей. А двухмерная фигура, образованная общими точками плоскости и многогранника, в этом случае называется сечением. Такое сечение будет являться диагональным, если одна из диагоналей основания принадлежит секущей плоскости.
Инструкция
Диагональное сечение куба имеет форму прямоугольника, площадь которого (S) нетрудно рассчитать, зная длину любого ребра (a) объемной фигуры. В этом прямоугольнике одной из сторон будет высота, совпадающая с длиной ребра. Длину другой – диагонали – рассчитайте по теореме Пифагора для треугольника, в котором она является гипотенузой, а два ребра основания – катетами. В общем виде ее можно записать так: a*√2. Площадь диагонального сечения найдите умножением двух его сторон, длины которых вы выяснили: S = a*a*√2 = a²*√2. Например, при длине ребра в 20 см площадь диагонального сечения куба должна быть примерно равна 20²*√2 ≈ 565,686 см².
Для вычисления площади диагонального сечения параллелепипеда (S) действуйте так же, но учитывайте, что в теореме Пифагора в этом случае участвуют катеты разной длины – длина (l) и ширина (w) объемной фигуры. Длина диагонали в этом случае будет равна √(l²+w²). Высота (h) тоже может отличаться от длин ребер оснований, поэтому в общем виде формула площади сечения может быть записана так: S = h*√(l²+w²). Например, если длина, высота и ширина параллелепипеда равны, соответственно, 10, 20 и 30 см, площадь его диагонального сечения составит приблизительно 30*√(10²+20²) = 30*√500 ≈ 670,82 см².
Диагональное сечение четырехугольной пирамиды имеет треугольную форму. Если высота (H) этого многогранника известна, а в его основании лежит прямоугольник, длины смежных ребер (a и b) которого тоже даны в условиях, расчет площади сечения (S) начните с вычисления длины диагонали основания. Как и в предыдущих шагах используйте для этого треугольник из двух ребер основания и диагонали, где по теореме Пифагора длина гипотенузы равна √(a²+b²). Высота пирамиды в таком многограннике совпадает с высотой треугольника диагонального сечения, опущенной на сторону, длину которой вы только что определили. Поэтому для нахождения площади треугольника найдите половину от произведения высоты на длину диагонали: S = ½*H*√(a²+b²). Например, при высоте в 30 см и длинах смежных сторон основания в 40 и 50 см площадь диагонального сечения должна быть примерно равна ½*30*√(40²+50²) = 15*√4100 ≈ 960,47 см².
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
как найти площадь диагонального сечения прямоугольного параллелепипеда?
Ксюня Дмитриева
Ученик
(100),
закрыт
14 лет назад
решение задачи даны основания 6дм и 8 дм высота параллелепипеда 8 дм
Villager
Ученик
(221)
14 лет назад
по главной диагонали:
Диагональ Д=квадр корень из (2*квадрат (8дм)) =8дм*корень из (2)
Площадь сечения S= Диагональ Д * 6дм
Для другой диагонали аналогично.
Лилия Сергеева
Мастер
(2183)
14 лет назад
Элементарно – все данные ву исходе, найди длину диогонали сечения и высчитывай плошщадь прямоуголника, полученного присечении. А лучше нарисуй – тогда можно просто измерить линейкой.
Как найти сечение параллелепипеда
Сечения геометрических фигур имеют различные формы. У параллелепипеда сечение всегда представляет собой прямоугольник или квадрат. Оно имеет ряд параметров, которые могут быть найдены аналитическим способом.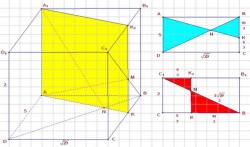
Через параллелепипед можно провести четыре сечения, которые представляют собой квадраты или прямоугольники. Всего он имеет два диагональных и два поперечных сечения. Как правило, они имеют разные размеры. Исключением является куб, у которого они одинаковы.
Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов – обычный и прямоугольный. У обычного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники или квадраты. Из этого следует,что куб – это частный случай прямоугольного параллелепипеда.
У любого сечения параллелепипеда есть определенные характеристики. Основными из них являются площадь, периметр, длины диагоналей. Если из условия задачи известны стороны сечения или какие-либо иные его параметры, этого достаточно, чтобы найти его периметр или площадь. По сторонам определяются также диагонали сечений. Первый из этих параметров – площадь диагонального сечения.
Для того чтобы найти площадь диагонального сечения, нужно знать высоту и стороны основания параллелепипеда. Если даны длина и ширина основания параллелепипеда, то диагональ найдите по теореме Пифагора:
d=√a^2+b^2.
Найдя диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:
S=d*h.
Периметр диагонального сечения тоже можно вычислять по двум величинам – диагонали основания и высоте параллелепипеда. В этом случае вначале найдите две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а затем сложите с удвоенным значением высоты.
Если провести плоскость, параллельную ребрам параллелепипеда, можно получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения найдите следующим образом:
S=a*h.
Периметр этого сечения найдите аналогичным образом по следующей формуле:
p=2*(a+h).
Последний случай возникает, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:
S=a*b – площадь сечения;
p=2*(a+b).
Основание прямого параллелепипеда — ромб, площади диагональных сечений параллелепипеда равны 4 и 3. Найдите полную поверхность параллелепипеда, если диагонали меньшего диагонального сечения параллелепипеда взаимно перпендикулярны.
Спрятать решение
Решение.
Введём обозначения (см. рис.). Пусть BB1D1D — меньшее диагональное сечение, тогда, так как диагонали перпендикулярны, а исходный параллелепипед прямой, BB1D1D — квадрат. Следовательно, боковые рёбра параллелепипеда равны корню из 3. Заметим, что площадь большего из сечений равна произведению большей диагонали основания на боковое ребро, откуда В основании параллелограмма лежит ромб, тогда диагонали основания перпендикулярны. По теореме Пифагора
то есть
Площадь полной поверхности равна сумме двух площадей основания и четырёх площадей боковых граней, в нашем случае:
Ответ: 14.
