Диаметр дерева граф как найти - Сайт, где вы сможете решить свои вопросы

Содержание

1 Диаметр дерева
- 1.1 Алгоритм
- 1.2 Реализация
- 1.3 Обоснование корректности
- 1.4 Оценка времени работы
2 Центр дерева
- 2.1 Определения
- 2.2 Алгоритм
  - 2.2.1 Наивный алгоритм
  - 2.2.2 Алгоритм для дерева за O(n)
3 См. также
4 Источники информации

Диаметр дерева

Определение:

Диаметр дерева (англ. diameter of a tree) — максимальная длина (в рёбрах) кратчайшего пути в дереве между любыми двумя вершинами.

Пусть дан граф . Тогда диаметром называется , где — кратчайшее расстояние между вершинами.

Алгоритм

Возьмём любую вершину и найдём расстояния до всех других вершин.

Возьмём вершину такую, что для любого . Снова найдём расстояние от до всех остальных вершин. Самое большое расстояние — диаметр дерева.

Расстояние до остальных вершин будем искать алгоритмом .

Реализация

//граф g представлен списком смежности 
int diameterTree(list<list<int>> g):        
    v = u = w = 0
    d = bfs(g, v)
    for i = 0, i < n, i++
         if d[i] > d[u]
              u = i
    d = bfs(g, u)
    for i = 0, i < n, i++
          if d[i] > d[w]
               w = i
    return d[w]

Обоснование корректности

Будем пользоваться свойством, что в любом дереве больше одного листа. Исключительный случай — дерево из одной вершины, но алгоритм сработает верно и в этом случае.

Теорема:

Искомое расстояние — расстояние между двумя листами.

Доказательство:

Пусть искомое расстояние — расстояние между вершинами , где не является листом. Так как не является листом, то её степень больше единицы, следовательно, из неё существует ребро в непосещённую вершину (дважды посетить вершину мы не можем).

После запуска алгоритма получим дерево .

Теорема:

В дереве не существует ребер между вершинами из разных поддеревьев некоторого их общего предка.

Доказательство:

Предположим, существует ребро между соседними поддеревьями:

Рассмотрим первую вершину, в которую приведет наш алгоритм, пусть это вершина , тогда в ходе рассмотрения всех смежных вершин мы добавим в список вершину , тем самым исключив возможность попадания их в разные поддеревья.

Мы свели задачу к нахождению вершины , такой что сумма глубин поддеревьев максимальна.

Докажем, что одно из искомых поддеревьев содержит самый глубокий лист.
Пусть нет, тогда, взяв расстояние от до глубочайшего листа, мы можем улучшить ответ.

Таким образом мы доказали, что нам нужно взять вершину с наибольшей глубиной после первого , очевидно, что ей в пару надо сопоставить вершину , такую что максимально. Вершину можно найти запуском из .

Оценка времени работы

Все операции кроме — .
работает за линейное время, запускаем мы его два раза. Получаем .

Центр дерева

Определения

Определение:

Эксцентриситет вершины (англ. eccentricity of a vertex) — , где — множество вершин связного графа .

Определение:

Радиус (англ. radius) — наименьший из эксцентриситетов вершин графа .

Определение:

Центральная вершина (англ. central vertex) — вершина графа , такая что

Определение:

Центр графа (англ. center of a graph) — множество всех центральных вершин графа .

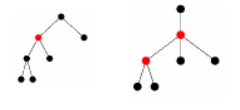
Примеры деревьев с одной и двумя центральными вершинами

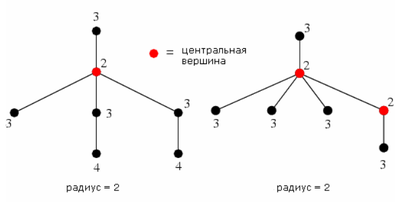
Графы, у которых показан эксцентриситет каждой вершины

Алгоритм

Наивный алгоритм

Найдём центр графа исходя из его определения.

Построим матрицу ( — мощность множества ), где , то есть матрицу кратчайших путей. Для её построения можно воспользоваться алгоритмом Флойда-Уоршелла или Дейкстры.
Подсчитаем максимум в каждой строчке матрицы . Таким образом, получим массив длины .
Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами.

Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет , а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и , за которую мы находим максимумы в матрице.

Алгоритм для дерева за O(n)

Теорема:

Каждое дерево имеет центр, состоящий из одной вершины или из двух смежных вершин.

Доказательство:

Утверждение очевидно для деревьев с одной и двумя вершинами. Покажем, что у любого другого дерева те же центральные вершины, что и у дерева , полученного из удалением всех его висячих вершин. Расстояние от данной вершины дерева до любой другой вершины достигает наибольшего значения, когда – висячая вершина. Таким образом, эксцентриситет каждой вершины дерева точно на единицу меньше эксцентриситета этой же вершины в дереве , следовательно, центры этих деревьев совпадают. Продолжим процесс удаления и получим требуемое.

Собственно, алгоритм нахождения центра описан в доказательстве теоремы.

Пройдёмся по дереву обходом в глубину и пометим все висячие вершины числом .
Обрежем помеченные вершины.
Образовавшиеся листья пометим числом и тоже обрежем.
Будем повторять, пока на текущей глубине не окажется не более двух листьев, и при этом в дереве будет тоже не более двух листьев.

Оставшиеся листья являются центром дерева.

Для того, чтобы алгоритм работал за , нужно обрабатывать листья по одному, поддерживая в очереди два последовательных по глубине слоя.

См. также

Дерево, эквивалентные определения
Дополнительный, самодополнительный граф

Источники информации

Wikipedia — Distance (graph theory)
Ф. Харари: Теория графов
А. Клебанов: Центры графов(нерабочая ссылка)

Источник

Доказываем корректность поиска диаметра дерева

Время на прочтение
3 мин

Количество просмотров 11K

Однажды на зачете мне попалась следующая задача. Придумайте алгоритм, находящий две вершины дерева с максимальным расстоянием друг от друга, и докажите его корректность. В тот момент я в принципе не знала, что у деревьев есть диаметр, радиус и много прочих вещей. Уже после зачета друг просветил меня, рассказав, что это за алгоритм, но без доказательства. Именно вопросом о доказательстве долгое время была забита моя голова. После прочтения нескольких статей, стало понятно, что материал не уляжется, пока самостоятельно себе не объясню все практически на пальцах (может, и читателю придется по вкусу). Перейдем от демагогии к сути.

Диаметр дерева — это максимальное расстояние между двумя вершинами в дереве. Алгоритм поиска состоит в двух запусках BFS. Первый идет от произвольной вершины дерева, во время обхода насчитываются расстояния от текущей вершины до всех других. Затем из них выбирается самая удаленная. Из нее делается второй запуск BFS. Насчитываются новые расстояния. Максимальное среди них и будет диаметром.

Почему этот простой с виду алгоритм работает корректно?

Чтобы избежать подводных камней при доказательстве, сразу обговорим случай с деревом из одной вершины и из двух вершин. Если вершина одна, то ребер у нас нет, первый BFS сообщит, что стартовая вершина имеет максимальную глубину, второй — тоже. По сути это и есть так, алгоритм сработает верно. Если имеется две вершины, то первый обход придет во вторую вершину, а второй — в стартовую, что корректно для данного случая.

Сначала поймем, что искомое расстояние — расстояние между двумя листами. На самом деле, пусть вершина на конце найденного максимального путь не является листом. Одновременно мы не можем увеличить искомое расстояние по предположению. Тем не менее, это означает, что BFS не посетил вершины, «расположенные за» текущей, что противоречит корректности BFS. Получается, что обе найденные вершины будут листьями. Прекрасно.

Подвесим наше дерево за вершину v, из которой запускаем первый обход.

Рассмотрим отдельный случай, когда вершина v сама является листом. В случае, если она и есть первый конец диаметра, то очевидно, что первый BFS найдет второй конец, а второй вернется в стартовую вершину. Иначе диаметр не будет проходить через v и также будет «перегибаться», так как не может содержать более двух листьев.

Пусть мы нашли диаметр и две вершины, ему соответствующие. Найдем LCA этих вершин a и b, назовем эту вершину c. Очевидно, что D = d[a,c] + d[c,b]. Фактически диаметр это сумма двух наиболее глубоких поддеревьев некоторой вершины, если она принадлежит длиннейшему пути. Диаметр дерева — это максимальный диаметр среди всех поддеревьев. Первый обход в ширину даст нам максимальную по глубине вершину (так как мы подвесили за стартовую вершину). Обозначим вершину на конце найденного пути w. Докажем, что w будет принадлежать искомому длиннейшему пути. Пусть диаметр «перегибается» в вершине c(он будет «перегибаться», так как соединяет два листа, а дерево подвешено за вершину v, не являющуюся листом). Пускай вершина w принадлежит одному из поддеревьев вершины c. Тогда просто заменим некоторую часть пути (c, x), где x — один из концов, на (c, w). d[c,x] < d[c,w]. Мы улучшили ответ. Значит, первоначальный путь не был диаметром. Если w является предком c, то w не является листом, поэтому этот случай отпадает. Если же w находится где-то в другом поддереве, то пусть e = LCA(c, w). d[w,e] — максимальная глубина поддерева e. Тогда так как e — предок c, то d[x, e] > d[x,c]. d[w,e] > d[y,e] > d[y,c]. Поэтому D0 = d[x,c] + d[y,c] < d[x, e] + d[w, e] = D. Значит, первоначально диаметр был найден неверно и вершина w принадлежит диаметру.

Примечание:

В данной части доказательства мы использовали свойство, что лист w имеет наибольшую глубину в любом поддереве данного дерева, которому принадлежит w. Докажем по индукции. База — один лист w. Очевидно, что утверждение верно. Пусть для некоторого поддерева это тоже верно, тогда поднимемся на уровень выше. Допустим, существует вершина, у которой глубина в текущем поддереве больше, чем у w. Назовем текущую вершину a, вершину с предполагаемой большей глубиной x, корень дерева v.
d[v,x] = d[v,a] + d[a,x];
d[v,w] = d[v,a] + d[a,w];
d[v,x] < d[v,w] в силу корректности работы BFS;
d[a,x] > d[a,w] по предположению;
В итоге получаем противоречие. Поэтому вершина w обладает наибольшей глубиной в любом поддереве.

Получаем, что вершина w принадлежит диаметру, а также является одним из его концов. Тогда очевидно, что остается лишь найти наиболее удаленную от w вершину, что и делает второй BFS.

При написании статьи использовались материалы:
neerc.ifmo.ru/wiki/index.php?title=%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC%D1%8B_%D0%BD%D0%B0_%D0%B4%D0%B5%D1%80%D0%B5%D0%B2%D1%8C%D1%8F%D1%85

Источник

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

The diameter of a tree (sometimes called the width) is the number of nodes on the longest path between two leaves in the tree. The diagram below shows two trees each with a diameter of five, the leaves that form the ends of the longest path are shaded (note that there is more than one path in each tree of length five, but no path longer than five nodes)

We have discussed a solution in the below post
Diameter of a binary tree
In this post, a different DFS-based solution is discussed. After observing the above tree we can see that the longest path will always occur between two leaf nodes. We start DFS from a random node and then see which node is farthest from it. Let the node farthest be X. It is clear that X will always be a leaf node and a corner of DFS. Now if we start DFS from X and check the farthest node from it, we will get the diameter of the tree.
The C++ implementation uses an adjacency list representation of graphs. STL‘s list container is used to store lists of adjacent nodes.

Implementation:

C++

#include <iostream>

#include <limits.h>

#include <list>

using namespace std;

int x;

void dfsUtil(int node, int count, bool visited[],

int& maxCount, list<int>* adj)

{

visited[node] = true;

count++;

for (auto i = adj[node].begin(); i != adj[node].end(); ++i) {

if (!visited[*i]) {

if (count >= maxCount) {

maxCount = count;

x = *i;

}

dfsUtil(*i, count, visited, maxCount, adj);

}

void dfs(int node, int n, list<int>* adj, int& maxCount)

{

bool visited[n + 1];

int count = 0;

for (int i = 1; i <= n; ++i)

visited[i] = false;

dfsUtil(node, count + 1, visited, maxCount, adj);

}

int diameter(list<int>* adj, int n)

{

int maxCount = INT_MIN;

dfs(1, n, adj, maxCount);

dfs(x, n, adj, maxCount);

return maxCount;

}

int main()

{

int n = 5;

list<int>* adj = new list<int>[n + 1];

adj[1].push_back(2);

adj[2].push_back(1);

adj[1].push_back(3);

adj[3].push_back(1);

adj[2].push_back(4);

adj[4].push_back(2);

adj[2].push_back(5);

adj[5].push_back(2);

cout << "Diameter of the given tree is "

<< diameter(adj, n) << endl;

return 0;

}

Java

import java.util.ArrayList;

import java.util.Arrays;

import java.util.List;

public class Diametre_tree {

static int x;

static int maxCount;

static List<Integer> adj[];

static void dfsUtil(int node, int count,

boolean visited[],

List<Integer> adj[])

{

visited[node] = true;

count++;

List<Integer> l = adj[node];

for(Integer i: l)

{

if(!visited[i]){

if (count >= maxCount) {

maxCount = count;

x = i;

}

dfsUtil(i, count, visited, adj);

}

static void dfs(int node, int n, List<Integer>

adj[])

{

boolean[] visited = new boolean[n + 1];

int count = 0;

Arrays.fill(visited, false);

dfsUtil(node, count + 1, visited, adj);

}

static int diameter(List<Integer> adj[], int n)

{

maxCount = Integer.MIN_VALUE;

dfs(1, n, adj);

dfs(x, n, adj);

return maxCount;

}

public static void main(String args[])

{

int n = 5;

adj = new List[n + 1];

for(int i = 0; i < n+1 ; i++)

adj[i] = new ArrayList<Integer>();

adj[1].add(2);

adj[2].add(1);

adj[1].add(3);

adj[3].add(1);

adj[2].add(4);

adj[4].add(2);

adj[2].add(5);

adj[5].add(2);

System.out.println("Diameter of the given " +

"tree is " + diameter(adj, n));

}

Python3

def dfsUtil(node, count):

global visited, x, maxCount, adj

visited[node] = 1

count += 1

for i in adj[node]:

if (visited[i] == 0):

if (count >= maxCount):

maxCount = count

x = i

dfsUtil(i, count)

def dfs(node, n):

count = 0

for i in range(n + 1):

visited[i] = 0

dfsUtil(node, count + 1)

def diameter(n):

global adj, maxCount

dfs(1, n)

dfs(x, n)

return maxCount

if __name__ == '__main__':

n = 5

adj, visited = [[] for i in range(n + 1)], [0 for i in range(n + 1)]

maxCount = -10**19

x = 0

adj[1].append(2)

adj[2].append(1)

adj[1].append(3)

adj[3].append(1)

adj[2].append(4)

adj[4].append(2)

adj[2].append(5)

adj[5].append(2)

print ("Diameter of the given tree is ", diameter(n))

C#

using System;

using System.Collections.Generic;

class GFG

{

static int x;

static int maxCount;

static List<int> []adj;

static void dfsUtil(int node, int count,

bool []visited,

List<int> []adj)

{

visited[node] = true;

count++;

List<int> l = adj[node];

foreach(int i in l)

{

if(!visited[i])

{

if (count >= maxCount)

{

maxCount = count;

x = i;

}

dfsUtil(i, count, visited, adj);

}

static void dfs(int node, int n,

List<int> []adj)

{

bool[] visited = new bool[n + 1];

int count = 0;

dfsUtil(node, count + 1, visited, adj);

}

static int diameter(List<int> []adj, int n)

{

maxCount = int.MinValue;

dfs(1, n, adj);

dfs(x, n, adj);

return maxCount;

}

public static void Main(String []args)

{

int n = 5;

adj = new List<int>[n + 1];

for(int i = 0; i < n + 1; i++)

adj[i] = new List<int>();

adj[1].Add(2);

adj[2].Add(1);

adj[1].Add(3);

adj[3].Add(1);

adj[2].Add(4);

adj[4].Add(2);

adj[2].Add(5);

adj[5].Add(2);

Console.WriteLine("Diameter of the given " +

"tree is " + diameter(adj, n));

}

Javascript

<script>

let x;

let maxCount;

let adj=[];

function dfsUtil(node,count,visited,adj)

{

visited[node] = true;

count++;

let l = adj[node];

for(let i=0;i<l.length;i++)

{

if(!visited[l[i]]){

if (count >= maxCount) {

maxCount = count;

x = l[i];

}

dfsUtil(l[i], count, visited, adj);

}

function dfs(node,n,adj)

{

let visited = new Array(n + 1);

let count = 0;

for(let i=0;i<visited.length;i++)

{

visited[i]=false;

}

dfsUtil(node, count + 1, visited, adj);

}

function diameter(adj,n)

{

maxCount = Number.MIN_VALUE;

dfs(1, n, adj);

dfs(x, n, adj);

return maxCount;

}

let n = 5;

adj = new Array(n + 1);

for(let i = 0; i < n+1 ; i++)

adj[i] = [];

adj[1].push(2);

adj[2].push(1);

adj[1].push(3);

adj[3].push(1);

adj[2].push(4);

adj[4].push(2);

adj[2].push(5);

adj[5].push(2);

document.write("Diameter of the given " +

"tree is " + diameter(adj, n));

</script>

Output

Diameter of the given tree is 4

Time Complexity: O(n), where n is the number of nodes
Auxiliary Space: O(n)

This article is contributed by Ankur Singh. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Last Updated :
15 Jul, 2022

Like Article

Save Article

Vote for difficulty

Current difficulty :
Medium

Источник

вступление

Как особый граф, дерево имеет много хороших свойств, и диаметр дерева – одно из них.

определение

Есть много похожих определений диаметра дерева. Но так как я не нашел более авторитетного определения, просто используйте мой родной язык, чтобы описать его.
Для дерева с неотрицательными весами ребер расстояние между двумя точками определяется как сумма весов ребер пути между двумя точками, а диаметр дерева равен расстояние между двумя наиболее удаленными точками Путь, также называемый расстоянием, как диаметр дерева.
Короче говоря, диаметр дерева – это диаметр дерева.Самый длинный простой путь。

природа

Два конца диаметра должны быть двумя листовыми узлами.
Самая удаленная от любой точки точка должна быть конечной точкой диаметра.
Для двух деревьев, если оба конца диаметра первого дерева равны (u, v), а концы диаметра второго дерева равны (x, y), два дерева соединены ребром, тогда диаметр нового дерева должны быть Две точки в u, v, x, y.

Доказательство природы

Очевидно, что доказательство опускается.
Случай 1: точка a находится на диаметре((u,v))на. Если существует точка b такая, что $ dis (a, b) gt dis (a, u) text {и} dis (a, b) gt dis (a, v) $, то (dis (b, v) text (или) dis (b, u) gt dis (u, v) ), который((u,v))Не диаметр дерева, противоречиво.
Случай 2. Точка А не в диаметре((u,v))на. Если существует точка b такая, что $ dis (a, b) gt dis (a, u) text {и} dis (a, b) gt dis (a, v) $, можно также взять одну из конечные точки диаметра(u)анализ.
Схема анализа выглядит следующим образом (на линии нарисована душа):

Примечание к изображению:(u),(v) Конечная точка диаметра,(c)за ((а, б) текст {и} (а, и) )Пересечение,(d)за ((а, и) текст {и} (v, и) )Точка пересечения.

из-за(dis(a,b) gt dis (a,u)) , Зная(dis(c,b) gt dis (c,u)), А потом получить(dis(d,b) gt dis (d,u)), В конце концов мы знаем(dis(v,b) gt dis (v,u)), который((u,v))Не диаметр дерева, противоречиво.
Если диаметр нового дерева не равен диаметру одного из двух исходных деревьев, тогда новый диаметр должен проходить через соединительный край двух деревьев, а часть нового диаметра в каждом исходном дереве должна быть самой дальней точкой. от точки соединения, то есть это должна быть конечная точка исходного диаметра дерева.

Алгоритм решения

Есть два вида временной сложности:(O(N)) Один из них – dp, а другой – жадный алгоритм.

Метод первый: динамическое программирование

Согласно определению, нам нужно только запросить максимальную длину цепи.
Сначала преобразуйте дерево в корневое дерево. Предполагать(f[i])Узел(i)Максимальная глубина поддерева корня, есть уравнение перехода состояний[f[i] = max_{j in s(i)}f[j]+1 quad text{where $s(i)$ is the set of the son nodes of node i.}]Затем через узел в поддереве(i)Наибольшая длина цепи составляет(f[i]) И второй по величине(f[j]) (Значение по умолчанию – 0) сумма. Достаточно записать максимальную длину цепочки в течение всего процесса обхода.

Метод 2: жадный алгоритм

По характеру диаметра дерева 2 нам нужно лишь немного подобрать(s)Запустите DFS (или BFS), чтобы найти самую дальнюю точку от точки, то есть одну из конечных точек диаметра, обозначенную как(u). Аналогично подчиненный узел(u)Вначале мы можем найти другую конечную точку(v), Диаметр дерева можно получить, записав расстояние во время процесса.
По сравнению с методом 1, метод 2 позволяет более удобно находить конец диаметра, а затем получать конкретный путь диаметра.

Code

Временно

Перепечатано по адресу: https://www.cnblogs.com/pisceskkk/p/10423535.html

Источник

Утверждение. Если для двух вершин существует маршрут, связывающий их, то обязательно найдется минимальный маршрут, соединяющий эти вершины. Обозначим длину этого маршрута через d(v, w).

Определение. Величину d(v, w) (конечную или бесконечную) будем называть расстоянием между вершинами v, w. Это расстояние удовлетворяет аксиомам метрики:

1) d(v, w) 0, причем d(v, w) = 0 тогда и только тогда, когда v=w;

2) d(v, w) = d(w, v);

3) d(v, w) d(v, u) + d(u, w).

Определение. Диаметром связного графа называется максимально возможное расстояние между двумя его вершинами.

Определение. Центром графа называется такая вершина, что максимальное расстояние между ней и любой другой вершиной является наименьшим из всех возможных; это расстояние называется радиусом графа.

Пример 82.

Для графа G, изображенного на рис. 3.16, найти радиус, диаметр и центры.

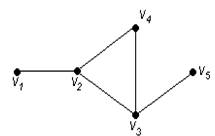
Рис. 3.16. Граф для примера 82

Решение.

Чтобы определить центры, радиус, диаметр графа G, найдем матрицу D(G) расстояний между вершинами графа, элементами d_ij которой будут расстояния между вершинами v_i и v_j. Для этого воспользуемся графическим представлением графа. Заметим, что матрица D(G) симметрична относительно главной диагонали.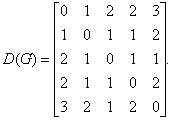

С помощью полученной матрицы для каждой вершины графа G определим наибольшее удаление из выражения: для i, j = 1, 2, …, 5. В результате получаем: r(v₁) = 3, r(v₂) = 2, r(v₃) = 2, r(v₄) = 2, r(v₅) = 3. Минимальное из полученных чисел является радиусом графа G, максимальное – диаметром графа G. Значит, R(G) = 2 и D(G) = 3, центрами являются вершины v₂, v₃, v₄.

Источник

Содержание