Напишите формулу нахождения диапазона частот.
Дмитрий Осадчий
Ученик
(126),
закрыт
9 лет назад
Дополнен 11 лет назад
длина звуковых волн, излучаемых скрипкой, может изменяться от 23мм до 1.3м. Каков диапазон частот скрипки?
Лучший ответ
Петро Хрiн
Гений
(95151)
11 лет назад
Частота в даном случае есть отношение скорости звука в воздухе (340 м/c) к длине волны в диапазоне0,023 м до1,3м, что соответствует частотам в диапазоне 261Гц до 14782Гц.
Остальные ответы
Ноябрь
Искусственный Интеллект
(145756)
11 лет назад
Угадай мелодию? Что ли?
Похожие вопросы
Частотный диапазон
- Частотный диапазон
-
Диапазо́н часто́т — полоса частот, которой присвоено условное наименование. Диапазон частот — одно из важнейших понятий радиотехники, а также физико-технических дисциплин в целом. Это понятие имеет общий характер, то есть можно говорить или о диапазоне рабочих частот какого-либо конкретного устройства, или о диапазоне, выделенном какой-то радиослужбе, или, например, об обобщённой разбивке всей полосы радиочастот.
Содержание
- 1 Диапазоны в радиотехнике
- 1.1 Диапазоны РЛС
- 1.2 Диапазоны в гражданской радиосвязи
- 2 Диапазоны в акустике
- 3 Литература и документация
- 3.1 Литература
- 3.2 Нормативные документы
- 4 Примечания
- 5 Ссылки
- 6 См. также
Диапазоны в радиотехнике
- Использование диапазонов по радиослужбам регламентируется Регламентом радиосвязи Российской Федерации и международными соглашениями.
- ГОСТ 24375 даёт следующую обобщённую разбивку радиочастотного диапазона, основанную на международных стандартах:
- Очень низкие частоты — 3—30 кГц, соответствует сверхдлинным волнам
- Низкие частоты — 30—300 кГц, соответствует длинным волнам
- Средние частоты — 300—3000 кГц, соответствует средним волнам
- Высокие частоты — 3—30 МГц, соответствует коротким волнам
- Очень высокие частоты — 30—300 МГц, соответствует ультракоротким (или метровым волнам)
- Ультравысокие частоты — 300—3000 МГц, соответствует дециметровым волнам
- Сверхвысокие частоты — 3—30 ГГц, соответствует сантиметровым волнам
- Крайне высокие частоты — 30—300 ГГц, соответствует миллиметровым волнам
- Гипервысокие частоты — 300—3000 ГГц, соответствует субмиллиметровым волнам
- Следует заметить, что вышеприведённая классификация не получила широкого распространения и в ряде случаев вступает в противоречие с национальными стандартами (ГОСТ) в области радиоэлектроники. На практике под низкочастотным диапазоном подразумевается звуковой диапазон, а под высокочастотным — весь радиодиапазон, выше 30 кГц, в том числе сверхвысокочастотный (свыше 300 МГц).
Традиционные обозначения частотных диапазонов на Западе сложились в ходе Второй мировой войны. В настоящее время они закреплены в США стандартом IEEE, а также международным стандартом ITU.
Диапазоны РЛС
Частотные диапазоны РЛС[1]
Диапазон Частоты Длина волны Примечания HF 3 — 30 МГц 10 — 100 м Радары береговой охраны, «загоризонтные» РЛС; (англ. high frequency) P < 300 МГц > 1 м ‘P’ от англ. previous, использовался в первых радарах VHF 50 — 330 МГц 0,9 — 6 м Обнаружение на больших дальностях, исследования земли; (англ. very high frequency) UHF 300 — 1000 MHz 0.3-1 m Обнаружение на больших дальностях (например, артиллерийского обстрела), исследования поверхности земли, лесов; (англ. ultra high frequency) L 1 — 2 ГГц 15 — 30 см наблюдение и контроль за воздушным движением; (англ. Long) S 2 — 4 ГГц 7,5 — 15 см управление воздушным движением, метеорология, морские радары; (англ. Short) C 4 — 8 ГГц 3,75 — 7,5 см метеорология,спутниковое вещание,промежуточный диапазон между X и S; (англ. Compromise) X 8 — 12 ГГц 2,5 — 3,75 см управление оружием, наведение ракет, морские радары, погода, картографирование среднего разрешения; в США диапазон 10,525ГГц ± 25МГц используется в РЛС аэропортов. Ku 12 — 18 ГГц 1,67 — 2,5 см картографирование высокого разрешения, спутниковая альтиметрия; (англ. under K) K 18 — 27 ГГц 1,11 — 1,67 см нем. kurz, то есть ‘короткий’; использование ограничено из-за сильного поглощения водяным паром, поэтому используются диапазоны Ku и Ka. Диапазон K используется для обнаружения облаков, в полицейских дорожных радарах (24,150 ± 0,100 ГГц). Ka 27 — 40 ГГц 0,75 — 1,11 см Картографирование, управление воздушным движением на коротких дистанциях, специальные радары, управляющие дорожными фотокамерами (34,300 ± 0,100 ГГц); (англ. above K) mm 40 — 300 ГГц 1 — 7,5 мм миллиметровые волны, делятся на два следующих диапазона V 40 — 75 ГГц 4,0 — 7,5 мм медицинские аппараты КВЧ, применяемые для физиотерапии, а также аппараты для диагностики (например, по методу Фолля) W 75 — 110 ГГц 2,7 — 4,0 мм сенсоры в экспериментальных автоматических транспортных средствах, высокоточные исследования погодных явлений Диапазоны в гражданской радиосвязи
В России для гражданской радиосвязи выделены три диапазона частот:
- 27 МГц (Си-Би, «Citizens’ Band», гражданский диапазон), с разрешённой выходной мощностью передатчика до 10 Вт;
- 433 МГц (LPD, “Low Power Device”), выделено 69 каналов для раций с выходной мощностью передатчика не более 0,01 Вт;
- 446 МГц (PMR, “Personal Mobile Radio”), выделено 8 каналов для раций с выходной мощностью передатчика не более 0,5 Вт.
Диапазоны в акустике
- Инфразвуковой — ниже 20 Гц
- Звуковой — от 20 Гц до 20 кГц
- Ультразвуковой — от 20 кГц до 1 ГГц
- Гиперзвуковой — свыше 1ГГц
Литература и документация
Литература
- Справочник по Радиоэлектронным системам: В 2-х томах/Под ред. Б. Х. Кривицкого — М.:Энергия, 1979
Нормативные документы
- ГОСТ 24375-80 Радиосвязь. Термины и определения
- Регламент радиосвязи Российской Федерации
Примечания
- ↑ По материалам статьи en:Radar
Ссылки
- Радиочастоты
- Соответствия частот канальных и частотных радиостанций LPD диапазона
См. также
- Частоты
- Частота периодического процесса
- Радиоизлучение
- 1 Диапазоны в радиотехнике
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое “Частотный диапазон” в других словарях:
-
частотный диапазон Ka — Диапазон выше (a = above) диапазона K. Нестандартное обозначение диапазона частот спутниковой связи 20 30 ГГц. [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN Ka band … Справочник технического переводчика
-
частотный диапазон Ku — Диапазон ниже under диапазона K. Нестандартное обозначение диапазона спутниковой связи: для восходящего потока (к спутнику) 14,0 14,5 ГГц и для нисходящего потока (от спутника) 11,7 12,2 ГГц. [http://www.iks… … Справочник технического переводчика
-
частотный диапазон L — Диапазон сверхвысоких частот (300 1550 МГц). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN L band … Справочник технического переводчика
-
частотный диапазон C — Нестандартное обозначение микроволнового диапазона спутниковая связи: для восходящего потока (к спутнику) 5,925 6,425 ГГц и для нисходящего потока (от спутника): 3,700 4,200 ГГц. Сигналы C диапазона незначительно ослабляются в условиях облачности … Справочник технического переводчика
-
частотный диапазон — 3.22 частотный диапазон: Для общих целей частотный диапазон состоит из октавных полос со среднегеометрическими частотами от 125 до 8000 Гц. Источник: ГОСТ ИСО 230 5 2002: Испытания станков. Часть 5. Определение шумовых характеристик … Словарь-справочник терминов нормативно-технической документации
-
частотный диапазон — dažnių diapazonas statusas T sritis automatika atitikmenys: angl. frequency band; frequency range vok. Frequenzband, n; Frequenzbereich, m rus. диапазон частот, m; частотный диапазон, m pranc. bande des fréquences, f; gamme des fréquences, f … Automatikos terminų žodynas
-
частотный диапазон (сейсмического канала записи) — Диапазон частот, в пределах которого неравномерность амплитудно частотной характеристики сейсмического канала записи не превышает 3 дБ относительно максимального уровня [ГОСТ 16821 91] Тематики сейсморазведка … Справочник технического переводчика
-
частотный диапазон измерений акселерометра — Диапазон частот измеряемых ускорений, в котором нормированы допускаемые погрешности акселерометра. [ГОСТ 18955 73] Тематики акселерометры EN frequency effective range of an accelerometer DE Meßfrequenzbereich eines Beschleunigungsaufnehmers FR… … Справочник технического переводчика
-
частотный диапазон сейсмоприемника — Диапазон частот, в пределах которого неравномерность амплитудно частотной характеристики сейсмоприемника относительно ее средней линейной части не превышает величины, установленной в нормативно технической документации. [ГОСТ 16821 91] Тематики… … Справочник технического переводчика
-
частотный диапазон электронного датчика [преобразователя физической величины] — Диапазон частот, в котором обеспечивается заданная неравномерность амплитудно частотной характеристики электронного датчика [преобразователя физической величины]. [ГОСТ Р 51086 97] Тематики датчики и преобразователи физических величин … Справочник технического переводчика
-
Частотный диапазон комплекта фильтров fm2 – fm1 — Диапазон частот между средними геометрическими частотами крайних фильтров комплекта Источник: ГОСТ 17168 82: Фильтры электронные октавные и третьоктавные. Общие технические … Словарь-справочник терминов нормативно-технической документации
Длина, скорость и частота электромагнитной волны.
Онлайн калькулятор перевода длины волны в частоту для широкого диапазона частот, включая радиоволны, микроволны, инфракрасное излучение,
видимый свет, ультрафи- олетовое излучение, рентгеновские и гамма лучи.
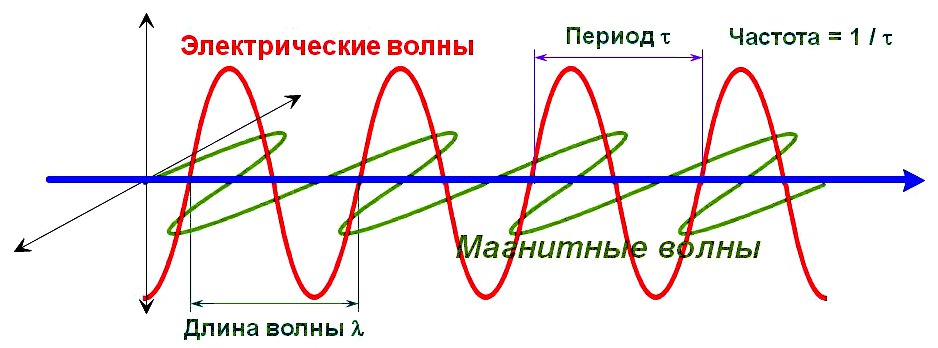
Электромагнитные колебания – это взаимосвязанные колебания электрического и магнитного полей, проявляющиеся в периодическом изменении
напряжённости (E) и индукции (B) поля в электроцепи или пространстве. Эти поля перпендикулярны друг другу в направлении движения волны
(Рис.1) и, в зависимости от частоты, представляют собой: радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое
излучение, рентгеновские либо гамма-лучи.
Рис.1
Длина волны, обозначаемая буквой λ и измеряемая в метрах –
это расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.
Другими словами, это расстояние, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π.
Время, за которое волна успевает преодолеть это расстояние (λ), т. е. интервал времени, за который периодический колебательный процесс
повторяется, называется периодом колебаний, обозначается буквой ፐ (тау) или Т и измеряется в метрах.
Частота электромагнитных колебаний связана с периодом простейшим соотношением:
f (Гц) = 1 / T (сек).
Скорость распространения электромагнитных волн в вакууме (v) равна скорости
света и составляет величину:
v = С = 299792458 м/сек.
В среде эта скорость уменьшается: v = С / n, где
n > 1 – это показатель преломления среды.
Абсолютный показатель преломления любого газа (в том числе воздуха) при обычных условиях мало чем отличается от единицы, поэтому
с достаточной точностью его можно не учитывать в условиях распространения электромагнитных волн в воздушном пространстве.
Соотношение, связывающее длину волны со скоростью распространения в общем случае, выглядит следующим образом:
λ (м) = v (м/сек) *Т (сек) = v (м/сек) / f (Гц).
И окончательно для воздушной среды:
λ (м) = 299792458 *Т (сек) = 299792458 / f (Гц).
Прежде чем перейти к калькуляторам, давайте рассмотрим шкалу частот и длин волн непрерывного диапазона электромагнитных волн,
которая традиционно разбита на ряд поддиапазонов. Соседние диапазоны могут немного перекрываться.
| Диапазон | Полоса частот | Длина волны |
| Сверхдлинные радиоволны | 3…30 кГц | 100000…10000 м |
| Длинные радиоволны | 30…300 кГц | 10000…1000 м |
| Средние радиоволны | 300…3000 кГц | 1000…100 м |
| Короткие радиоволны | 3…30 МГц | 100…10 м |
| Метровый радиодиапазон | 30…300 МГц | 10…1 м |
| Дециметровый радиодиапазон | 300…3000 МГц | 1…0,1 м |
| Сантиметровый СВЧ диапазон | 3…30 ГГц | 10…1 см |
| Микроволновый СВЧ диапазон | 30…300 ГГц | 1…0,1 см |
| Инфракрасное излучение | 0,3…405 ТГц | 1000…0,74 мкм |
| Красный цвет | 405…480 ТГц | 740…625 нм |
| Оранжевый цвет | 480…510 ТГц | 625…590 нм |
| Жёлтый цвет | 510…530 ТГц | 590…565 нм |
| Зелёный цвет | 530…600 ТГц | 565…500 нм |
| Голубой цвет | 600…620 ТГц | 500…485 нм |
| Синий цвет | 620…680 ТГц | 485…440 нм |
| Фиолетовый цвет | 680…790 ТГц | 440…380 нм |
| Ультрафиолетовое излучение | 480…30000 ТГц | 400…10 нм |
| Рентгеновское излучение | 30000…3000000 ТГц | 10…0,1 нм |
| Гамма излучение | 3000000…30000000 ТГц | 0,1…0,01 нм |
А теперь можно переходить к калькуляторам.
КАЛЬКУЛЯТОР РАСЧЁТА ДЛИНЫ ВОЛНЫ ПО ЧАСТОТЕ
|
Частота электромагнитных колебаний f |
||
Показатель преломления среды (по умолч. 1) |
||
Длина волны |
КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ДЛИНЕ ВОЛНЫ
|
Длина электромагнитной волны в вакууме λ |
||
Частота |
В радиочастотной практике имеет распространение величина Kp, называемая коэффициентом укорочения. Однако здесь
существует некоторая путаница. Одни источники интерпретируют эту величину, как отношение длины волны в среде к длине волны в вакууме,
т. е. численно равной Kp = 1/n, где n – это, как мы помним, показатель преломления среды.
Другие, наоборот – как отношение длины волны в вакууме к длине волны в среде, т. е. Kp = n.
Поэтому надо иметь в виду – если Kp > 1, то значение показателя преломления среды, которое следует подставлять в калькулятор n = Kp, а
если Kp < 1, то n = 1/Kp.
Частотный диапазон
Диапазон частот — это полоса частот, воспроизводимая системой в определенных пределах по амплитуде (уровню громкости) сигнала.
Частотный диапазон усилителя
Диапазон частот вычисляется на основе данных графика амплитудно-частотной характеристики.
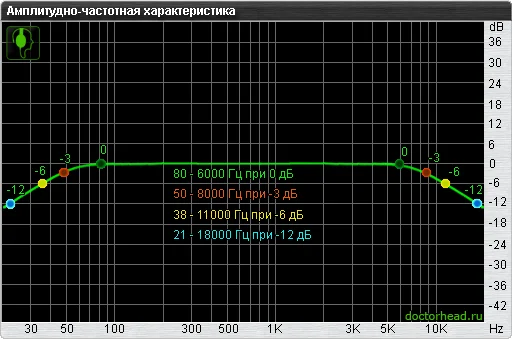
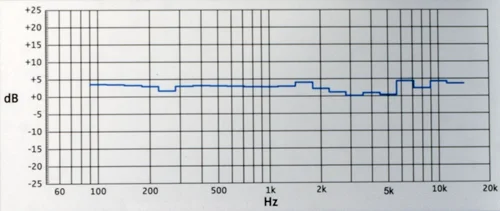
Амплитудно-частотная характеристика усилителя как правило представляет собой кривую близкую к прямой, со спадами (уменьшением уровня сигнала) на краях. В технической документации указывается частотный диапазон, попадающий в определенные рамки по амплитуде. В примере показаны частотные диапазоны для отклонения на 0, 3, 6 и 12 дБ. Как правило, чем больше отклонение, тем более широкая полоса частот попадает в диапазон частот. Если отклонение не указано, то указанный частотный диапазон не несет полезной или определенной информации. У усилителя обычно не бывает резкого падения амплитуды на АЧХ, поэтому если указано, что диапазон частот 30 Гц — 18000 Гц по уровню -1 дБ, то например частоты 20 Гц и 25000 Гц усилитель так же воспроизводит, просто с уровнем меньшим, нежели -1 дБ. Это может быть -3 дБ, а может -5 дБ. Формально, частотный диапазон указывать производителей никто не обязывает и его указывают просто, чтобы был. Если не указано в каких пределах отклонений обозначен частотный диапазон, то производитель лишь утверждает, что усилитель эти частоты воспроизводит, и что этот уровень не соответствует полной тишине.
Частотный диапазон наушников
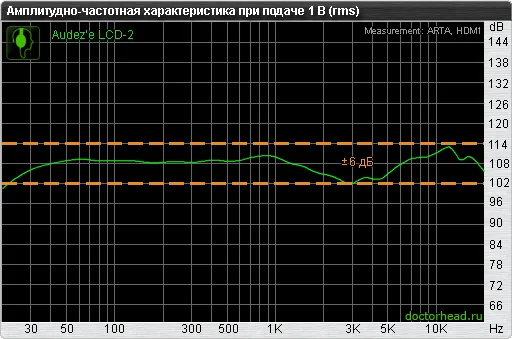
Амплитудно-частотная характеристика наушников, как правило, представляет собой кривую, где неравномерность кривой может достигать как малых, так и относительно высоких величин. Диапазон частот может иметь вид 25 Гц — 28000 Гц ± 6 дБ, что означает что линия графика не выходит за пределы в 6 дБ относительно среднего положения линии, где расстояние между линиями отклонения (коридором значений) равно 12 дБ. В примере это пунктирные оранжевые линии. Обозначение 25 Гц — 28000 Гц — 12 дБ будет обозначать то же самое. По смыслу в таком обозначении за базовую среднюю линию взята верхняя линия коридора. В коридоре, обозначаемом как “—”, могут не учитываться пики и провалы на средних частотах.
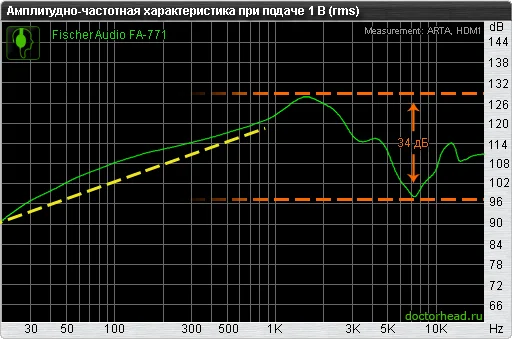
Однако бывает так, что линия графика имеет более высокие отклонение по пикам и провалам, и частотная характеристика уже может выглядеть как 30 Гц — 20000 Гц ± 17 дБ, что не дает представление о характере звучания. Высокие отклонения могут быть продиктованы в подчеркнутости определенных частотных диапазонов для особого характера звучания или профессиональных целей. Так же линия графика может плавно убывать (в примере — в области низких частот), что делает затруднительным указание края частотного диапазона, так как более низкая звучит лишь немного тише, чем более верхняя, а не замолкает. И в таком случае частотный диапазон может указываться или для одного из стандартных значений ± 3, ± 6 дБ, или произвольно. Как правило, практика обозначения коридора “± 3 / ± 6 дБ” применяется для акустических систем.
Особая сложность заключается в том, что стенды для измерений наушников имеют разные конфигурации и не имеют жесткого стандарта, в отличии от акустических систем. АЧХ на разных стендах имеют расхождения, а характер амплитудно-частотной характеристики не располагает к обозначениям в рамках коридора или отклонения амплитудно-частотной характеристики от какой либо базовой частоты. В итоге производители устанавливают частотный диапазон, исходя из своих соображений, и лишь на редкие модели указывается коридор или отклонение. Без указания коридора или отклонения, цифры несут скорее маркетинговый характер, нежели показывают реальное положение дел. Ориентироваться на такие цифры в сравнительных целях между моделями наушников смысла нет. Также стоит учесть, что указывать частотный диапазон, чувствительность, импеданс и другую техническую информацию производители совершенно не обязаны и перечень указываемых характеристик продиктован в большей степени самим рынком, если компания считает, что указание данных поднимет продажи, то указывает, если считает наоборот, то не указывает.
Для сравнения звучания наушников, с точки зрения того, какие частоты они воспроизводят, а какие нет, стоит исходя из графиков амплитудно-частотной характеристики, измеренных в одинаковых условиях.
Обычно частотный диапазон на упаковке указан без обозначения отклонений и условий измерений. Такие данные не дают возможности прямого сравнения, т.к. для одних наушников мог изначально применяться коридор в 6 дБ, а для других в 20 дБ, и наушники с меньшим частотным диапазоном на практике могут играть более уверенно, против модели с указанным широким частотным диапазоном.
Примеры
Характерный вид обозначений частотного диапазона, который не рекомендуется сравнивать с частотными диапазонами других наушников.
В таком виде дается обозначение частотного диапазона у подавляющего количества наушников — вне зависимости от их стоимости или области применения.
Данные, которые можно приблизительно сравнивать, имеют указание коридора значений. В данном случае для Sennheiser HD800 указано два частотных диапазона с разным коридором в 3 и 10 дБ. Дополнительно прикладывается и типовая амплитудно-частотная характеристика, по которой можно составить различные частотные диапазоны в разных коридорах.
В данном примере коридоры можно построить лишь в диапазоне 90 Гц — 14000 Гц, где присутствует линия графика. Указанные выше коридоры и график дополняют друг друга.
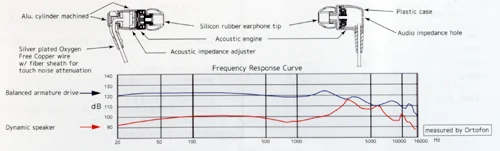
Производитель может дать информацию по частотному диапазону без коридора, но в совокупности с амплитудно-частотной характеристикой.
В примере показан Ortofon e-Q7, где указан частотный диапазон без коридора и подробный график амплитудно-частотной характеристики в частотном диапазоне от 20 до 16 000 Гц.
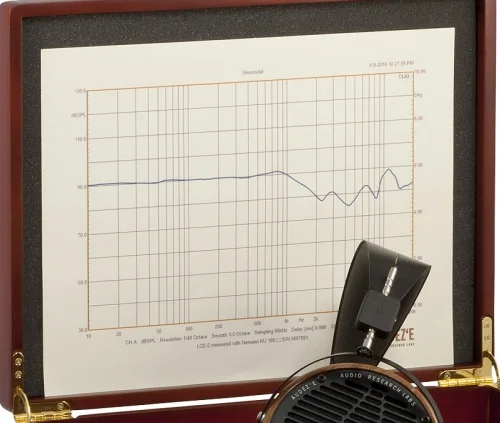
К наушникам также может прилагаться подробная амплитудно-частотная характеристика, как это сделано, например, в случае с Audez’e LCD-2.
Download Article
Download Article
Frequency, also called wave frequency, is a measurement of the total number of vibrations or oscillations made within a certain amount of time. There are a few different ways to calculate frequency based on the information you have available to you. Keep reading to learn some of the most common and useful versions.
-
1
Learn the formula. The formula for frequency, when given wavelength and the velocity of the wave, is written as: f = V / λ[1]
- In this formula, f represents frequency, V represents the velocity of the wave, and λ represents the wavelength of the wave.
- Example: A certain sound wave traveling in the air has a wavelength of 322 nm when the velocity of sound is 320 m/s. What is the frequency of this sound wave?
-
2
Convert the wavelength into meters, if necessary. If the wavelength is given in nanometers, you need to convert this value into meters by dividing it by the number of nanometers in a single meter.[2]
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 322 nm
- 322 nm x (1 m / 10^9 nm) = 3.22 x 10^-7 m = 0.000000322 m
Advertisement
-
3
Divide the velocity by the wavelength. Divide the velocity of the wave, V, by the wavelength converted into meters, λ, in order to find the frequency, f.[3]
- Example: f = V / λ = 320 / 0.000000322 = 993788819.88 = 9.94 x 10^8
-
4
Write your answer. After completing the previous step, you will have completed your calculation for the frequency of the wave. Write your answer in Hertz, Hz, which is the unit for frequency.
- Example: The frequency of this wave is 9.94 x 10^8 Hz.
Advertisement
-
1
Learn the formula. The formula for the frequency of a wave in a vacuum is almost identical to that of a wave not in a vacuum. Since there are no outside influences on the velocity of the wave, though, you would use the mathematical constant for the speed of light, which electromagnetic waves would travel at under these conditions. As such, the formula is written as: f = C / λ[4]
- In this formula, f represents frequency, C represents the velocity or speed of light, and λ represents the wavelength of the wave.
- Example: A particular wave of electromagnetic radiation has a wavelength of 573 nm when passing through a vacuum. What is the frequency of this electromagnetic wave?
-
2
Convert the wavelength into meters, if necessary. When the problem gives you the wavelength in meters, no further action is needed. If, however, the wavelength is given in micrometers, you need to convert this value into meters by dividing it by the number of micrometers in a single meter.
- Note that when working with extremely small numbers or extremely large numbers, it is generally easier to write the values in scientific notation. The values will be shown in and out of their scientific notation forms for this example, but when writing your answer for homework, other schoolwork, or other formal forums, you should stick with scientific notation.
- Example: λ = 573 nm
- 573 nm x (1 m / 10^9 nm) = 5.73 x 10^-7 m = 0.000000573
-
3
Divide the speed of light by the wavelength. The speed of light is a constant, so even if the problem does not provide you with a value, the value remains 3.00 x 10^8 m/s. Divide this value by the wavelength converted into meters.[5]
- Example: f = C / λ = 3.00 x 10^8 / 5.73 x 10^-7 = 5.24 x 10^14
-
4
Write your answer. With this, you should have calculated the value of the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 5.24 x 10^14 Hz.
Advertisement
-
1
Learn the formula. Frequency and the time taken to finish a single wave oscillation are inversely proportional. As such, the formula for calculating frequency when given the time taken to complete a wave cycle is written as: f = 1 / T
- In this formula, f represents frequency and T represents the time period or amount of time required to complete a single wave oscillation.
- Example A: The time for a certain wave to complete a single oscillation is 0.32 seconds. What is the frequency of this wave?
- Example B: In 0.57 seconds, a certain wave can complete 15 oscillations. What is the frequency of this wave?
-
2
Divide the number of oscillations by the time period. Usually, you will be told how long it takes to complete a single oscillation, in which case, you would just divide the number 1 by the time period, T. If given a time period for numerous oscillations, however, you will need to divide the number of oscillations by the overall time period required to complete them.[6]
- Example A: f = 1 / T = 1 / 0.32 = 3.125
- Example B: f = 1 / T = 15 / 0.57 = 26.316
-
3
Write your answer. This calculation should tell you the frequency of the wave. Write your answer in Hertz, Hz, the unit for frequency.
- Example A: The frequency of this wave is 3.125 Hz.
- Example B: The frequency of this wave is 26.316 Hz.
Advertisement
-
1
Learn the formula. When told the angular frequency of a wave but not the standard frequency of that same wave, the formula to calculate the standard frequency is written as: f = ω / (2π)[7]
- In this formula, f represents the frequency of the wave and ω represents the angular frequency. As with any mathematical problem, π stands for pi, a mathematical constant.
- Example: A particular wave rotates with an angular frequency of 7.17 radians per second. What is the frequency of that wave?
-
2
Multiply pi by two. In order to find the denominator of the equation, you need to double the value of pi, 3.14.
- Example: 2 * π = 2 * 3.14 = 6.28
-
3
Divide the angular frequency by the double of pi. Divide the angular frequency of the wave, given in radians per second, by 6.28, the doubled value of pi.[8]
- Example: f = ω / (2π) = 7.17 / (2 * 3.14) = 7.17 / 6.28 = 1.14
-
4
Write your answer. This final bit of calculation should indicate what the frequency of the wave is. Write your answer in Hertz, Hz, the unit for frequency.
- Example: The frequency of this wave is 1.14 Hz.
Advertisement
Add New Question
-
Question
What is the frequency if 80 oscillations are completed in 1 second?
Frequency is the number of oscillations completed in a second. The answer would be 80 Hertz.
-
Question
Do atoms have a frequency and, if so, does it mean everything vibrates?
Atoms have energy. Energy is often characterized as vibration. Vibration possesses frequency. So, yes, everything could be thought of as vibrating at the atomic level.
-
Question
What’s the definition of frequency?
The rate at which a vibration occurs that constitutes a wave, either in a material (as in sound waves), or in an electromagnetic field (as in radio waves and light), usually measured per second. The rate at which something occurs or is repeated over a particular period of time or in a given sample.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To calculate the frequency of a wave, divide the velocity of the wave by the wavelength. Write your answer in Hertz, or Hz, which is the unit for frequency. If you need to calculate the frequency from the time it takes to complete a wave cycle, or T, the frequency will be the inverse of the time, or 1 divided by T. Display this answer in Hertz as well. Keep reading to learn how to calculate frequency from angular frequency!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,511,957 times.