Диффузионный ток как найти

From Wikipedia, the free encyclopedia

Diffusion current is a current in a semiconductor caused by the diffusion of charge carriers (electrons and/or electron holes). This is the current which is due to the transport of charges occurring because of non-uniform concentration of charged particles in a semiconductor. The drift current, by contrast, is due to the motion of charge carriers due to the force exerted on them by an electric field. Diffusion current can be in the same or opposite direction of a drift current. The diffusion current and drift current together are described by the drift–diffusion equation.^[1]

It is necessary to consider the part of diffusion current when describing many semiconductor devices. For example, the current near the depletion region of a p–n junction is dominated by the diffusion current. Inside the depletion region, both diffusion current and drift current are present. At equilibrium in a p–n junction, the forward diffusion current in the depletion region is balanced with a reverse drift current, so that the net current is zero.

The diffusion constant for a doped material can be determined with the Haynes–Shockley experiment. Alternatively, if the carrier mobility is known, the diffusion coefficient may be determined from the Einstein relation on electrical mobility.

Overview[edit]

Diffusion current versus drift current[edit]

The following table compares the two types of current:

Diffusion current	Drift current
Diffusion current = the movement caused by variation in the carrier concentration.	Drift current = the movement caused by electric fields.
Direction of the diffusion current depends on the slope of the carrier concentration.	Direction of the drift current is always in the direction of the electric field.
Obeys Fick’s law:	Obeys Ohm’s law:

Carrier actions[edit]

No external electric field across the semiconductor is required for a diffusion current to take place. This is because diffusion takes place due to the change in concentration of the carrier particles and not the concentrations themselves. The carrier particles, namely the holes and electrons of a semiconductor, move from a place of higher concentration to a place of lower concentration. Hence, due to the flow of holes and electrons there is a current. This current is called the diffusion current. The drift current and the diffusion current make up the total current in the conductor. The change in the concentration of the carrier particles develops a gradient. Due to this gradient, an electric field is produced in the semiconductor.

Derivation[edit]

In a region where n and p vary with distance, a diffusion current is superimposed on that due to conductivity. This diffusion current is governed by Fick’s Law:

where:

F is flux.

D_e is the diffusion coefficient or diffusivity

is the concentration gradient of electrons

there is a minus sign because the direction of diffusion is opposite to that of the concentration gradient

The diffusion coefficient for a charge carrier is related to its mobility by the Einstein relation:

where:

k_B is the Boltzmann constant

T is the absolute temperature

e is the electrical charge of an electron

Now let’s focus on the diffusive current in one-dimension along the x-axis:

The electron current density J_e is related to flux, F, by:

Thus

Similarly for holes:

Notice that for electrons the diffusive current is in the same direction as the electron density gradient because the minus sign from the negative charge and Fick’s Law cancel each other out. However, holes have positive charges and therefore the minus sign from Fick’s Law is carried over.

Superimpose the diffusive current on the drift current to get

for electrons

and

for holes

Consider electrons in a constant electric field E. Electrons will flow (i.e. there is a drift current) until the density gradient builds up enough for the diffusion current to exactly balance the drift current. So at equilibrium there is no net current flow:

Example[edit]

Some or all of the formulas presented in this article have missing or incomplete descriptions of their variables, symbols or constants which may create ambiguity or prevent full interpretation. Please assist in recruiting an expert or improve this article yourself. See the talk page for details. (June 2012)

To derive the diffusion current in a semiconductor diode, the depletion layer must be large compared to the mean free path.
One begins with the equation for the net current density J in a semiconductor diode,

(1)

where D is the diffusion coefficient for the electron in the considered medium, n is the number of electrons per unit volume (i.e. number density), q is the magnitude of charge of an electron, μ is electron mobility in the medium, and E = −dΦ/dx (Φ potential difference) is the electric field as the potential gradient of the electric potential. According to the Einstein relation on electrical mobility and . Thus, substituting E for the potential gradient in the above equation (1) and multiplying both sides with exp(−Φ/V_t), (1) becomes:

(2)

Integrating equation (2) over the depletion region gives

which can be written as

(3)

where

The denominator in equation (3) can be solved by using the following equation:

Therefore, Φ* can be written as:

(4)

Since the x ≪ x_d, the term (x_d − x/2) ≈ x_d, using this approximation equation (3) is solved as follows:

,

since (Φ_i − V_a) > V_t. One obtains the equation of current caused due to diffusion:

(5)

From equation (5), one can observe that the current depends exponentially on the input voltage V_a, also the barrier height Φ_B. From equation (5), V_a can be written as the function of electric field intensity, which is as follows:

(6)

Substituting equation (6) in equation (5) gives:

(7)

From equation (7), one can observe that when a zero voltage is applied to the semi-conductor diode, the drift current totally balances the diffusion current. Hence, the net current in a semiconductor diode at zero potential is always zero.

The equation above can be applied to model semiconductor devices. When the density of electrons is not in equilibrium, diffusion of electrons will occur. For example, when a bias is applied to two ends of a chunk of semiconductor, or a light is shining in one place (see right figure), electrons will diffuse from high density regions (center) to low density regions (two ends), forming a gradient of electron density. This process generates diffusion current.

See also[edit]

• Alternating current
• Conduction band
• Convection–diffusion equation
• Direct current
• Drift current
• Free electron model
• Random walk
• Maximal Entropy Random Walk – diffusion in agreement with quantum predictions

References[edit]

• Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
• Concepts of Modern Physics (4th Edition), A. Beiser, Physics, McGraw-Hill (International), 1987, ISBN 0-07-100144-1
• Solid State Physics (2nd Edition), J.R. Hook, H.E. Hall, Manchester Physics Series, John Wiley & Sons, 2010, ISBN 978 0 471 92804 1
• Ben G. Streetman, Santay Kumar Banerjee; Solid State Electronic Devices (6th Edition), Pearson International Edition; pp. 126–135.
• “Differences between diffusion current”. Diffusion. Archived from the original on 13 August 2017. Retrieved 10 September 2011.
• “Carrier Actions of Diffusion Current”. Diffusion. Archived from the original on 10 August 2011. Retrieved 11 October 2011.
• “derivation of difusion current”. Archived from the original on 14 December 2011. Retrieved 15 October 2011.

Лекция
8

1. Диффузионный ток.
   Законы движения носителей заряда в
   полупроводниках

Диффузия
(diffusio) в переводе с латыни
означает распространение, растекание,
рассеивание. Диффузия – это перенос
частиц разной природы, обусловленный
хаотическим тепловым движением молекул
(атомов) при наличии градиента концентрации
частиц. Диффузия имеет место как в газах
и жидкостях, так и в твердых телах и не
связана с электрическим зарядом частиц.
Диффузия происходит в направлении
падения концентрации вещества и ведёт
к выравниванию концентрации вещества
в первоначально неоднородной среде.
Эту аналогию можно распространить и на
явления, происходящие в результате
неравномерного распределения концентрации
носителей заряда в объеме полупроводника
в отсутствии градиента температуры.

В
полупроводниках может возникать
диффузионный ток, которым называется
направленное перемещение носителей
заряда в сторону меньшей концентрации
за счет собственной энергии (т.е. за счет
теплового движения). Поясним появление
диффузионного тока при одномерном
случае.

Рис.
1. Движение дырок при наличии разности
концентраций

Если
носители заряда распределены равномерно
по полупроводнику, то их концентрация
является равновесной. Под влиянием
каких-либо внешних воздействий в разных
частях полупроводника концентрация
может быть неодинаковой. Например, если
часть полупроводника подвергнуть
действию излучения, то в ней усилится
генерация пар носителей и возникнет
дополнительная концентрация носителей,
называемая избыточной. Следовательно,
избыточные носители заряда не находятся
в тепловом равновесии с решеткой и
поэтому называются неравновесными.
В отличие от равновесных они могут
неравномерно распределяться по объему
полупроводника.

Неравномерное
распределение неравновесных носителей
зарядов сопровождается их диффузией в
сторону меньшей концентрации. Это
движение носителей зарядов (электронов
и дырок) обусловливает прохождение
электрического тока, называемого
диффузионным
.
Этот ток так же, как ток проводимости,
может быть электронным и дырочным.

Главной
характеристикой диффузии служит
плотность диффузионного тока

– количество носителей заряда, переносимых
в единицу времени через единицу площади
поверхности, перпендикулярной направлению
переноса.

Плотности
диффузионных токов определяются законом
Фика:

,

,

где
величины

и

являются градиентами концентрации, а
D_n
и D_p
– коэффициентами диффузии.

Градиент
концентрации характеризует, насколько
резко меняется концентрация вдоль оси
x(одномерный случай),
т. е. каково изменение концентрации n
или p на
единицу длины. Если разности концентраций
нет, то ∆n = 0
или ∆p = 0
и ток диффузии не возникает. Чем больше
изменение концентрации ∆n
или ∆p на данном
расстоянии ∆x,
тем больше ток диффузии.

Знак
«минус» в формуле плотности дырочного
диффузионного тока указывает на то, что
дырочный ток направлен в сторону
уменьшения концентрации дырок. Это
поясняет рис. 1, на котором показано, что
если концентрация дырок p возрастает
с увеличением координаты x, то дырки
двигаются в сторону, противоположную
положительному направлению оси x.
Следовательно, дырочный ток в этом
случае надо считать отрицательным
(рис.2).

Рис. 2.
Диффузионный ток в полупроводниках n-
и p-типа

Коэффициенты
диффузии D_n,,
D_p
– количество носителей заряда,
пересекающих в единицу времени единичную
площадку, перпендикулярную к выбранному
направлению, при градиенте концентрации
в этом направлении, равном единице. Это
параметры дрейфового движения.

Параметры
дрейфового и диффузионного движения
связаны между собой соотношениям
Эйнштейна

;

,

где
,
— коэффициент диффузии и подвижность
электронов;
,
— коэффициент диффузии и подвижность
дырок.

Эти
соотношения строго выполняются лишь
для невырожденных полупроводников в
условиях равновесия.

Соотношение
Эйнштейна имеет простой физический
смысл: независимо от причины,
вызвавшей направленное движение,
свободные носители встречают на своем
пути одни и те же неоднородности
(препятствия), при взаимодействии с
которыми происходит рассеяние. Поэтому
между основными параметрами дрейфового
и диффузионного движений μ и D
существует некая пропорциональность.
Коэффициент
пропорциональности

имеет размерность потенциала (вольт)
и называется тепловым потенциалом.

Поэтому
все описанные выше зависимости подвижности
носителей заряда могут быть использованы
и для коэффициентов диффузии с учетом
множителя φ_т. (рис. 3).

Коэффициент
диффузии в основном зависит от температуры,
типа носителя, материала полупроводника,
степени легирования, центров рассеяния.

Исследования
показывают, что

и
.

Таблица 1

Коэффициент
диффузии носителей в чистых полупроводниках
при комнатной температуре

	Германий	Кремний	Арсенид галлия	Антимонид индия
, см2/с	100	36	260	до 1750
, см2/с	45	13	12	17

При
низких температурах, когда преобладает
рассеяние на примесях, D ~ T^5/2,
а при высоких температурах D ~ T^-1/2.
Различие температурной зависимости
подвижности и коэффициента диффузии
приводит к тому, что с ростом температуры
относительная роль диффузионного
движения увеличивается.

Рис.
3. Зависимости подвижности и коэффициента
диффузии от концентрации примесей для
полупроводников Si
и GaAs при комнатной
температуре

Зная
характер изменения подвижностей и
соотношения Эйнштейна можно подучить
зависимость коэффициентов диффузии от
температуры

,

где
D₀ – коэффициент
диффузии при температуре Т₀.

Аналогично
можно определить зависимость коэффициентов
диффузии от концентрации примесей

,

где
D₀ – коэффициент
диффузии при концентрации примесей N₀.

Если
за счет какого-то внешнего воздействия
в некоторой части полупроводника создана
избыточная концентрация носителей, а
затем внешнее воздействие прекратилось,
то избыточные носители будут рекомбинировать
и распространяться путем диффузии в
другие части полупроводника.

Избыточная
концентрация начнет убывать по
экспоненциальному закону, показанному
графически на рис. 4 для электронной
концентрации.

Рис. 4.
Изменение избыточной концентрации в
пространстве

Расстояние
L_n,
на котором избыточная концентрация
неравновесных носителей уменьшается
в е (2,72) раз, т. е. становится равной 0,37
первоначального значения n₀,
называют диффузионной длиной в
полупроводнике р-типа. Она характеризует
убывание избыточной концентрации в
пространстве.

Скорость
рекомбинации неравновесных носителей
(рис.5) пропорциональна избыточной
концентрации дырок (p_n
– p_n0)
и электронов (n_p
– n_p0):

,

где
τ_p – время жизни
дырок; τ_n – время
жизни электронов.

Рис. 5.
Изменение избыточной концентрации во
времени

Время,
в течение которого избыточная концентрация
уменьшится в е (2,72) раз, т. е. станет равна
0,37 от первоначального значения n_изб(0),
называют временем жизни неравновесных
носителей τ_n.
Этой величиной характеризуют процесс
убывания избыточной концентрации во
времени. Рекомбинация неравновесных
носителей происходит внутри полупроводника
и на его поверхности и сильно зависит
от примесей, а также от состояния
поверхности. Значения τ_n
для германия и кремния в различных
случаях могут быть долей микросекунды
до сотен микросекунд и более.

Таким
образом, убывание избыточной концентрации
происходит во времени и в пространстве
и поэтому величины τ_n
и L_n
оказываются связанными друг с другом
следующей зависимостью:

.

Из
уравнения можно сказать, что с увеличением
температуры уменьшается D_n
, резко возрастает τ_n
и возрастает диффузионная длина.

Если
в полупроводнике существует и электрическое
поле, и градиент концентрации носителей,
полный проходящий ток будет иметь
дрейфовую и диффузионную составляющие.
В таком случае плотности токов
рассчитываются по следующим уравнениям:

.

Таким
образом, плотность общего тока i
любой точке неоднородного полупроводника
в любой момент времени будет определяться
уравнением

.

Следовательно,
для определения тока необходимо знать
концентрацию носителей и напряженность
поля. В общем случае концентрации p
и n зависят от двух
переменных: координаты х и времени
t. Поэтому для
определения токов нужно предварительно
найти функции

и
.
Эти функции являются решениями так
называемых уравнений непрерывности
потока, которым в любой момент времени
подчиняется движение носителей.

При
отсутствии внешних факторов (свет,
радиация и т.п.) уравнения непрерывности
для дырок и электронов записываются в
виде

,

.

Если
напряженность Е меняется вдоль оси
х (т.е. если в полупроводнике имеется
существенный объемный заряд), приходится
дополнительно привлекать уравнение
Пуассона, которое в одномерном случае
имеет вид

,

где
λ – плотность заряда, ε₀ –
электрическая постоянная, ε – относительная
диэлектрическая проницаемость.

Из
этих уравнений следует вывод: изменение
концентраций носителей заряда в
полупроводнике с течением времени
происходит из-за рекомбинации (первые
слагаемые правых частей), перемещения
вследствие диффузии (вторые слагаемые)
и дрейфа (третьи и четвертые слагаемые).

Решение
системы уравнений в общем виде невозможно.
В каждом конкретном случае приходится
вводить те или иные упрощения.

Соседние файлы в папке Конспект лекций

• #
• #
• #
• #
• #
• #
• #

ДИФФУЗИОННЫЙ ТОК

ДИФФУЗИОННЫЙ ТОК, электродный ток в условиях, когда скорость электрохим. р-ции определяется скоростью подвода реагирующего в-ва к пов-сти электрода или отвода от этой пов-сти продуктов р-ции.
Перенос реагирующих в-в в р-ре электролита может осуществляться по трем механизмам: диффузии, миграции и конвекции. Соотв. поток в-ва от электрода или к нему можно рассматривать как сумму диффузионной, миграционной и конвективной составляющих. Первая обусловлена наличием градиента концентрации в-ва с в направлении х от электрода в т. наз. диффузионном слое, где концентрация изменяется от значения в объеме жидкости до значения на пов-сти электрода за счет расходования из р-ра или образования в-ва в электрохим. р-ции. Вторая связана с миграцией ионов из-за наличия градиента электрич. потенциала дЕ/дх в диффузионном слое. Третья связана с переносом в-ва к электроду или от него потоком жидкости в межэлектродном пространстве. Скорость движения р-ра v уменьшается при приближении к электроду и в простейшем случае становится равной нулю на его пов-сти. Поэтому выражение для диффузионного тока содержит два слагаемых – диффузионное и миграционное. При этом v оказывает влияние на диффузионный ток, изменяя толщину диффузионного слоя, т. е. градиенты концентрации и потенциала, к-рые увеличиваются при увеличении v.
В разб. р-рах электролитов для плотности i_j диффузионный ток частиц j-го сорта (катионов):



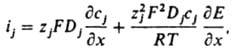
где z_j и D_j – соотв. зарядовое число и коэф. диффузии ионов j-го сорта, F – постоянная Фарадея, R – газовая постоянная, T – абс. т-ра.
Решение системы ур-ний приведенного здесь типа для частиц всех сортов, имеющихся в р-ре, при определенных условиях м. б. использовано для разл. практич. целей, напр., для расчета т. н. предельного диффузионного тока, к-рый достигается при обращении в нуль приэлектродной концентрации разряжающихся на электроде частиц. Измеряя величину предельного диффузионного тока (Вольтамперометрия)или переходное время, за к-рое достигается предельный диффузионный ток (Хронопотенцометрия), можно проводить количеств. анализ р-ров (определять с_j) или определять D_j.

===
Исп. литература для статьи «ДИФФУЗИОННЫЙ ТОК»: Ньюмен Дж., Электрохимические системы, пер. с англ., М., 1977, с. 243-330; Дамаскин Б. Б., Петрий О. А., Введение в электрохимическую кинетику, 2 изд. М.. 1983, с. 143-228. А. Д. Давыдов.

Страница «ДИФФУЗИОННЫЙ ТОК» подготовлена по материалам химической энциклопедии.

Диффузионный ток – это ток в полупроводнике, вызванный диффузией носителей заряда (дырок и / или электронов). Это ток, который возникает из-за переноса зарядов, происходящего из-за неоднородной концентрации заряженных частиц в полупроводнике. Дрейфовый ток, напротив, возникает из-за движения носителей заряда из-за силы, действующей на них со стороны электрического поля. Диффузионный ток может быть в том же направлении, что и ток дрейфа, или в противоположном направлении. Диффузионный ток и дрейфовый ток вместе описываются уравнением дрейфа-диффузии.

. При описании многих полупроводниковых приборов необходимо учитывать часть диффузионного тока. Например, в токе около области истощения p – n-перехода преобладает диффузионный ток. Внутри обедненной области присутствует как диффузионный, так и дрейфовый ток. В состоянии равновесия в p – n-переходе прямой диффузионный ток в обедненной области уравновешивается обратным дрейфовым током, так что чистый ток равен нулю.

постоянная диффузии для легированного материала может быть определена с помощью эксперимента Хейнса-Шокли. В качестве альтернативы, если известна подвижность носителей, коэффициент диффузии можно определить из соотношения Эйнштейна для электрической подвижности.

Содержание

• 1 Обзор
  • 1.1 Диффузионный ток в зависимости от тока дрейфа
  • 1.2 Действия носителя
• 2 Получение
• 3 Пример
• 4 См. Также
• 5 Ссылки

Обзор

Диффузионный ток в зависимости от тока дрейфа

В следующей таблице сравниваются два типа тока :

Диффузионный ток	Дрейфовый ток
Диффузионный ток = движение, вызванное изменением концентрации носителей.	Дрейфовый ток = движение, вызванное электрическими полями.
Направление диффузионного тока зависит от крутизны концентрации носителей.	Направление дрейфового тока всегда совпадает с направлением электрического поля.
Соблюдается закон Фика : J = – q D d ρ dx { displaystyle J = -qD { frac {d rho} {dx}}}	Соблюдается Закон Ома : J = q ρ μ E { displaystyle J = q rho mu E}

Воздействие носителя

Для создания внешнего электрического поля через полупроводник не требуется должен иметь место диффузионный ток. Это связано с тем, что диффузия происходит из-за изменения концентрации частиц носителя, а не самих концентраций. Частицы-носители, а именно дырки и электроны полупроводника, перемещаются из места с более высокой концентрацией в место с более низкой концентрацией. Следовательно, из-за потока дырок и электронов возникает ток. Этот ток называется диффузионным. Дрейфовый ток и диффузионный ток составляют полный ток в проводнике. Изменение концентрации частиц носителя имеет градиент. Из-за этого градиента в полупроводнике создается электрическое поле.

Вывод

Чтобы получить диффузионный ток в полупроводниковом диоде, обедненный слой должен быть большим по сравнению со средней длиной свободного пробега. Первый начинается с уравнения для чистой плотности тока Дж в полупроводниковом диоде,

J = qn μ E + q D dndx { displaystyle J = qn mu E + qD { frac {dn } {dx}}}

(1)

где D – коэффициент диффузии для электрона в рассматриваемой среде, n – количество электронов в единице объема (т.е. числовая плотность), q – величина заряда электрона, μ – подвижность электрона в среде, а E = −dΦ / dx (Φ разность потенциалов) – электрическое поле как градиент потенциала электрического потенциала . Согласно соотношению Эйнштейна для электрической подвижности D = μ V t { displaystyle D = mu V_ {t}}и V t = k T / д { Displaystyle V_ {т} = кТ / д}. Таким образом, подставляя E для градиента потенциала в приведенном выше уравнении (1) и умножая обе стороны на exp (−Φ / V t), (1) становится:

J e – Φ / V T знак равно Q D (- N V T ∗ d Φ dx + dndx) е – Φ / V t знак равно q D ddx (ne – Φ / V t) { Displaystyle Je ^ {- Phi / V_ {т }} = qD left ({ frac {-n} {V_ {t}}} * { frac {d Phi} {dx}} + { frac {dn} {dx}} right) e ^ {- Phi / V_ {t}} = qD { frac {d} {dx}} (ne ^ {- Phi / V_ {t}})}

(2)

Интегрирующее уравнение (2) над областью обеднения дает

J = q D ne – Φ / V t | 0 xd ∫ 0 xde – Φ / V tdx { displaystyle J = { frac {qDne ^ {- Phi / V_ {t}} { big |} _ {0} ^ {x_ {d}}} { int _ {0} ^ {x_ {d}} e ^ {- Phi / V_ {t}} dx}}}

который можно записать как

J = q DN ce – Φ B / V t [е V a / V t – 1] ∫ 0 xde – Φ ∗ / V tdx { displaystyle J = { frac {qDN_ {c} e ^ {- Phi _ {B} / V_ {t}} left [e ^ {V_ {a} / V_ {t}} – 1 right]} { int _ {0} ^ {x_ {d}} e ^ {- Phi ^ {*} / V_ {t}} dx}}}

(3)

где

Φ ∗ = Φ B + Φ i – V a { displaystyle Phi ^ {*} = Phi _ {B} + Phi _ {i } -V_ {a}}

Знаменатель в уравнении (3) может быть решен с помощью следующего уравнения:

Φ = – q N d 2 E s (x – xd) 2 { displaystyle Phi = – { frac {qN_ {d}} {2E_ {s} (x-x_ {d}) ^ {2}}}}

Следовательно, Φ * можно записать как:

Φ ∗ = q N dx E s (xd – x 2) = (Φ i – V a) xxd { displaystyle Phi ^ {*} = { frac {qN_ {d} x} {E_ {s}}} left ( x_ {d} – { frac {x} {2}} right) = ( Phi _ {i} -V_ {a}) { frac {x} {x_ {d}}}}

( 4)

Поскольку x << xd, член (x d – x / 2) ≈ x d, с использованием этого уравнения аппроксимации (3) решается следующим образом минимумы:

∫ 0 xde – Φ ∗ / V tdx = xd Φ i – V a V t { displaystyle int _ {0} ^ {x_ {d}} e ^ {- Phi ^ {*} / V_ {t}} dx = x_ {d} { frac { Phi _ {i} -V_ {a}} {V_ {t}}}},

, поскольку (Φ i – V а)>V t. Получаем уравнение тока, вызванного диффузией:

J = q 2 DN c V t [2 q E s (Φ i – V a) N d] 1/2 e – Φ B / V t (e V a / V t – 1) { displaystyle J = { frac {q_ {2} DN_ {c}} {V_ {t}}} left [{ frac {2q} {E_ {s}}} ( Phi _ {i} -V_ {a}) N_ {d} right] ^ {1/2} e ^ {- Phi _ {B} / V_ {t}} (e ^ {V_ {a} / V_ {t}} – 1)}

(5)

Из уравнения (5) можно заметить, что ток экспоненциально зависит от входного напряжения V a, а также от высоты барьера Φ B. Из уравнения (5), V a можно записать как функцию напряженности электрического поля, которая выглядит следующим образом:

E max = [2 q E s (Φ i – V a) N d] 1/2 { displaystyle E _ { mathrm {max}} = left [{ frac {2q} {E_ {s}}} ( Phi _ {i} -V_ {a}) N_ {d } right] ^ {1/2}}

(6)

Подстановка уравнения (6) в уравнение (5) дает:

J = q μ E max N ce – Φ B / В T (е В a / V t – 1) { displaystyle J = q mu E _ { mathrm {max}} N_ {c} e ^ {- Phi _ {B} / V_ {t}} ( e ^ {V_ {a} / V_ {t}} – 1)}

(7)

Из уравнения (7) можно заметить, что при приложении нулевого напряжения к полупроводниковому диоду, дрейфовый ток полностью уравновешивает диффузионный ток. Следовательно, чистый ток в полупроводниковом диоде при нулевом потенциале всегда равен нулю.

Поскольку носители генерируются (зеленые: электроны и пурпурный: дырки) из-за света, сияющего в центре собственного полупроводника, они рассеиваются к двум концам. Электроны имеют более высокую константу диффузии, чем дырки, что приводит к меньшему количеству избыточных электронов в центре по сравнению с дырками.

Пример

Вышеприведенное уравнение можно применить для моделирования полупроводниковых устройств. Когда плотность электронов не находится в равновесии, происходит диффузия электронов. Например, когда смещение применяется к двум концам куска полупроводника или свет светит в одном месте (см. Рисунок справа), электрон будет рассеиваться из областей с высокой плотностью (центр) в области с низкой плотностью (два конца), образуя градиент электронной плотности. Этот процесс генерирует диффузионный ток.

См. Также

• Переменный ток
• Зона проводимости
• Уравнение конвекции-диффузии
• Постоянный ток
• Дрейфовый ток
• Модель свободных электронов
• Случайное блуждание
• Максимальное Entropy Random Walk – диффузия в соответствии с квантовыми предсказаниями

Ссылки

• Encyclopaedia of Physics (2nd Edition), RG Лернер, Г. Л. Тригг, издательство VHC, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
• Концепции современной физики (4-е издание), A. Beiser, Physics, McGraw-Hill (International), 1987, ISBN 0-07-100144-1
• Физика твердого тела (2-е издание), JR Hook, HE Холл, Manchester Physics Series, John Wiley Sons, 2010, ISBN 978 0 471 92804 1
• Бен Г. Стритман, Сантай Кумар Банерджи; Твердотельные электронные устройства (6-е издание), международное издание Pearson; С. 126–135.
• «Различия между диффузионными токами». Распространение. Архивировано из оригинала 13 августа 2017 года. Дата обращения 10 сентября 2011.
• «Действия несущей диффузионного тока». Распространение. Архивировано из оригинала 10 августа 2011 года. Дата обращения 11 октября 2011 года.
• «происхождение диффузионного тока». Архивировано из оригинала 14 декабря 2011 г. Получено 15 октября 2011 г.

В полупроводниковых приборах могут протекать дрейфовый и диффузионный токи. Дрейфовым называется ток, обусловленный электрическим полем. Если к полупроводнику приложить внешнее электрическое поле, то в нем наблюдается направленное движение дырок вдоль поля и направленное движение электронов в противоположном направлении. Суммарный дрейфовый ток электронов и дырок определяется выражением

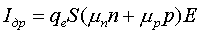, (1.2.)

где n и p — число электронов и дырок, пересекающих площадь в 1 см²/с; S — площадь поперечного сечения полупроводника.

Диффузионный ток обусловлен перемещением носителей заряда из области с высокой концентрацией в область с более низкой концентрацией, т. е. обусловлен наличием градиента концентрации (dn/dx — градиент концентрации электронов; dp/dx — градиент концентрации дырок). Суммарный диффузионный ток электронов и дырок определяется соотношением

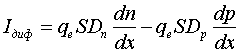, (1.3.)

где D_n и D_p — коэффициенты диффузии электронов и дырок соответственно.

Коэффициент диффузии равен числу носителей заряда, диффундирующих за одну секунду через единичную площадку при единичном градиенте концентрации. Знак «минус» в формуле означает, что диффузия происходит в направлении уменьшения концентрации, а так как дырки имеют положительный заряд, то диффузионный ток будет положительным при dp/dx<0.

Коэффициенты диффузии зависят от типа полупроводника, концентрации примесей, температуры и состояния кристаллической решетки. Например, при комнатной температуре для германия D_n » 100 см ²/с, D_р» 47 см²/с для кремния D_n » 30 см²/с, D_p »13cм²/c.

Коэффициент диффузии связан с подвижностью носителей заряда соотношением Эйнштейна:

Общий ток в полупроводнике может содержать четыре составляющие:

.

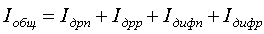Концентрация носителей заряда в электронном объеме полупроводника может изменяться за счет генерации и рекомбинации носителей, а также при возбуждении полупроводника (например, при освещении, действии внешнего электрического или магнитного поля). При возбуждении полупроводника концентрация подвижных носителей заряда — электронов (n) и дырок (p)- превышает равновесную концентрацию (n₀ и p₀). Это приводит к увеличению проводимости полупроводника. Электроны или дырки проводимости, не находящиеся в термодинамическом равновесии, называются неравновесными носителями заряда.

После прекращения действия возбуждающего фактора избыточные концентрации носителей заряда (например, электронов Dn = n – n₀) стремятся к нулю в результате процесса рекомбинации. При этом главную роль играют особые центры рекомбинации — ловушки, обладающие локальными энергетическими уровнями в запрещенной зоне. Они способны захватить электрон из зоны проводимости и дырку из валентной зоны, осуществляя их рекомбинацию. Такими ловушками являются дефекты кристаллической решетки внутри и на поверхности полупроводника.

Скорость уменьшения концентрации неравновесных носителей заряда 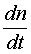вследствие рекомбинации характеризуется временем жизни неравновесных носителей заряда t_н:

,

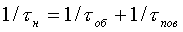где t_об — объемное время жизни неравновесных носителей заряда; t_пов — поверхностное время жизни неравновесных носителей заряда. Объемное время жизни уменьшается с ростом плотности дефектов решетки. Увеличение концентрации примесей в полупроводнике также уменьшает t_об. Максимальное значение t_об имеет собственный полупроводник.

На поверхности полупроводника имеется большое количество различных дефектов, которым соответствуют в запрещенной зоне незанятые энергетические уровни, играющие роль ловушек. Скорость поверхностной рекомбинации зависит от геометрии полупроводника, состояния поверхности и подвижности носителей заряда.

Спад начальной избыточной концентрации Dn(0) во времени подчиняется экспоненциальному закону

.

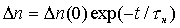Следовательно, время жизни неравновесных носителей можно определить интервалом времени, за которое избыточная концентрация уменьшается в е раз. Результирующая скорость спада избыточной концентрации в полупроводнике

.

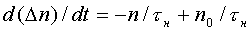Здесь n/t_н представляет собой скорость рекомбинации и зависит от мгновенного значения избыточной концентрации носителей заряда, а n₀/t_н — скорость генерации носителей заряда, которая зависит от равновесной концентрации носителей заряда. Величина t_н является временем жизни избыточных носителей, одинаковым для электронов и дырок и близким к времени жизни неосновных носи гелей. Зная время t_н, можно определить среднее расстояние, которое проходят носители заряда. Оно называется диффузионной длиной L. Так, для электронов

.

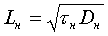Концентрация носителей заряда зависит от координаты X и времени t. Скорость изменения концентрации носителей заряда зависит от избыточной концентрации, ее градиента и пространственной производной градиента. Эту зависимость можно найти, решая уравнение непрерывности. Для потока дырок в полупроводнике n-типа оно имеет вид:

.

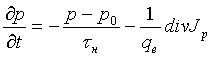Дивергенция вектора плотности потока характеризует скорость накопления (или рассасывания) носителей заряда в элементарном объеме полупроводника, обусловленную неравенством втекающих и вытекающих потоков носителей. В одномерном случае

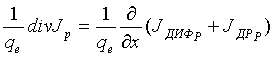, (1.4.)

где J_{ДИФ Р} – плотность диффузионного тока дырок; J_{ДР Р} – плотность дрейфового тока дырок. Учитывая, что

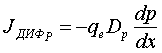, a ,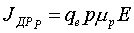

и подставляя эти выражения, получаем

.

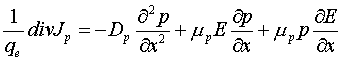С учетом последнего выражения уравнение непрерывности принимает вид:

.

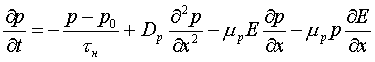Аналогично можно получить уравнение непрерывности для потока электронов в полупроводнике p-типа. Оно имеет вид:

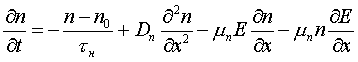. (1.5.)

Уравнение непрерывности позволяет проводить анализ процессов в полупроводниковых приборах.