Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —– | —– | 100.0 | 100.0 | —– | —– |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Показатели
динамики
– это показатели, характеризующие
изменение во времени уровней ряда. К
ним относятся: абсолютный прирост, темп
роста, темп прироста и абсолютное
значение одного процента прироста,
пункт роста.
1)
Абсолютный
прирост – определяется,
как разность между текущим и базисным
уровнями динамического ряда и показывает
на сколько текущий уровень превышает
базисный. Базисный абсолютный прирост
вычисляется по формуле: DYiб =Yi-Y0;
цепной абсолютный прирост: DYiц= Yi-Yi-1.
Цепные
и базисные абсолютные приросты связаны
между собой: сумма последовательных
цепных абсолютных приростов равна
базисному приросту последнего периода
(момента) времени.
2)
Темп роста
– определяется
как отношение текущего уровня к базисному
и показывает, во сколько раз текущий
уровень превышает базисный.
а)
базисный:
б)
цепной:
Между цепными
и базисным коэффициентами роста
существует взаимосвязь:
произведение последовательных цепных
коэффициентов роста равно базисному
коэффициенту роста за весь промежуток
времени; а частное от деления текущего
базисного коэффициента роста на
предыдущий базисный коэффициент роста
равно текущему цепному коэффициенту
роста.
3)
Темп прироста
– показывает,
на сколько процентов уровень текущего
периода (момента) времени больше (или
меньше) базисного уровня.
Базисный:
Цепной:
4)
Абсолютное значение 1% прироста –
рассчитывается
как отношение абсолютного цепного
прироста к цепному темпу прироста за
тот же период времени.
Используется для
правильной оценки значения полученного
темпа прироста. Аi показывает
какое абсолютное значение скрывается
за относительным показателем 1% прироста.
40. Средние показатели ряда динамики
Для
обобщающей характеристики динамики
исследуемого явления определяют
средние показатели динамики:
средний уровень ряда и средние показатели
изменения уровней ряда.
Средние
уровни ряда
определяются для интервальных
рядов с равноотстоящими
интервалами по формуле средней
арифметической простой
;
n
– число уровней ряда
Для
интервального
ряда с неравноотстоящими
интервалами средние уровни ряда
определяется по формуле средней
арифметической взвешенной
;
– длительность интервала времени между
уровнями
Для
моментных
рядов
с равноотстоящими
интервалами средние уровни ряда
определяются по формуле средней
хронологической простой
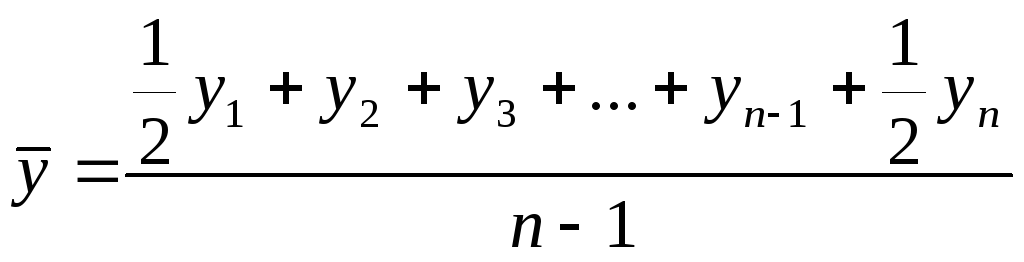
n
– количество дат
Для
моментных
рядов
с неравноотстоящими
датами средние уровни ряда определяются
по формуле средней хронологической
взвешенной
–
период времени между двумя смежными
датами
Средние
показатели изменения уровней
ряда рассчитываются
усреднением цепных показателей
динамики.
1)
Средний абсолютный прирост
определяется как простая средняя
арифметическая величина из цепных
абсолютных приростов и показывает, на
сколько в среднем изменялся показатель
в течение изучаемого периода времени:
2)
Средний
темп роста
определяется как средняя геометрическая
из цепных темпов роста и показывает,
сколько процентов в среднем составлял
рост показателя.
,
где
n – количество периодов времени.
4.
Средний
темп прироста показывает
на сколько процентов в среднем рос
показатель в течение изучаемого периода
времени.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы получить выраженные в числах изменения социальной и экономической среды, в статистике применяются разные методы. Среди них выделяется упорядочивание данных с использованием временной последовательности. Ряд динамики – это статистические значения в хронологическом порядке.
Ряд динамики может состоять из:
- значений, связанных с определенным моментом, – датой, днем, и др.;
- данных, связанных с периодом времени. Уровень ряда динамики это и есть полученный показатель.
Виды рядов динамики
Объединение радов происходит по:
- Времени. Это моментные и интервальные ряды.
- Форме представления. К ним относятся абсолютные, относительные и средние величины.
- Интервалам времени. Подразделяются на равномерные и неравномерные ряды.
- Числу смысловых статистических величин. Это изолированные и комплексные ряды.
Чтобы без ошибок построить динамические ряды, необходимо сопоставлять уровни рядов разных периодов. Для этого у них должны быть однородные величины. Также ряды предполагают охват явления с одинаковой полнотой.
Не допускать погрешностей в анализе динамики помогает смыкание рядов динамики. Суть понятия в проведении подготовительной работы до основных расчетов. Во время подготовки ряды объединяются в один. Уровни этих рядов рассчитаны по разным методологиям. Смыкание также включает преобразования, при которых абсолютные уровни рядов приводятся к общему основанию. Это действие помогает избежать несопоставимости уровней.
Анализ показателей в рядах динамики
Ряд динамики характеризует изменения данных внутри этого ряда. Статистические данные необходимо сравнивать также между рядами. По формулам можно определить основные показатели.
Разность уровней ряда динамики называется абсолютным приростом. Показатель демонстрирует, на сколько изменился каждый последующий уровень.
∆УЦ=Уi-Уi-1,
где Уi – уровень У1-УЦ,
Уi-1 – уровень предыдущего периода.
Отношение уровней ряда динамики называется темпом (коэффициентом) роста. По нему видно, во сколько раз изменились последовательные значения.
τp=УiУi-1,
где У1 – начальный уровень ряда.
Темп прироста. Показывает процентное отличие между последовательными уровнями.
Тпр=Тр-1
Если сравнивать между собой числа без всякой системы, не получится грамотно проанализировать ситуацию и выстроить новую стратегию. Например, продвижение продукта на основе маркетинговой стратегии. Использование формул поможет высчитать, какую прибыль принесло компании конкретное решение за анализируемый период.
Анализ показателей за длительный промежуток
Если есть задача оценить изменения, которые касаются длинного временного отрезка, эффективно применить средние показатели. В статистике для их определения используются следующие понятия.
Средний уровень ряда динамики. Применим для интервальных равноотстоящих рядов
→y=∑yn,
где n – число уровней ряда.
Если ряды неравноотстоящие, средний уровень интервального ряда динамики определяется как
→y=∑yt∑t,
где t – длина интервалов времени между уровнями.
Использование перечисленных методов позволяет применять полученные значения в экономике. Определять эффективность финансовых вложений, прогнозировать результаты. В управление предприятиями и бухгалтерию также можно внедрить данные методы для планирования и распределения бюджета.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание курса лекций «Статистика»
Статистическое изучение динамики социально-экономических явлений
Процессы и явления социально-экономической жизни общества, являющиеся предметом изучения статистики, находятся в постоянном движении и изменении. Для того, чтобы выявить тенденции и закономерности социально-экономического развития явлений, статистика строит особые ряды статистических показателей, которые называются рядами динамики (иногда их называют временными рядами), то есть ‑ это ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. В англоязычной литературе для временных рядов используется термин «time series». Ряды динамики получаются в результате сводки и обработки материалов периодического статистического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности. Значения показателя, составляющие ряд динамики, называются уровнями ряда.
Каждый ряд динамики характеризуется двумя параметрами: значениями времени и соответствующими им значениями уровней ряда. Уровни ряда обычно обозначаются «yt»: y1, y2 и т.д. В качестве показателя времени в рядах динамики могут указываться отдельные периоды (сутки, месяцы, кварталы, годы и т.д.) времени или определенные моменты (даты). Время в рядах динамики обозначается через «t».
Ряд динамики состоит из двух элементов:
1) уровня ряда (значения изучаемого показателя);
2) моментов (периодов) времени, когда фиксируется этот показатель.
Основные способы обработки рядов динамики:
1) укрупнение интервалов и расчет для них средних показателей;
2) сглаживание уровней способом скользящей средней;
3) выравнивание по аналитическим формулам.
Суть последнего способа заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени.
Ряды динамики, как правило, представляют в виде таблицы или графически.
Ряды динамики могут быть классифицированы по следующим признакам:
В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом ряды динамики абсолютных величин рассматриваются как исходные, а ряды относительных и средних величин ‑ как производные.
Ряды динамики абсолютных величин наиболее полно характеризуют развитие процесса или явления, например, грузооборота транспорта, инвестиций в основной капитал, добычи топлива, уставного капитала коммерческих банков и т.д.
Ряды относительных величин могут характеризовать во времени темпы роста (или снижения) определенного показателя; изменение удельного веса того или иного показателя в совокупности или изменение показателей интенсивности отдельных явлений, например, удельного веса приватизированных предприятий в той или иной отрасли; производства продукции на душу населения; структуры инвестиций в основной капитал по отраслям экономики, индекса потребительских цен и т.д.
Ряды динамики средних величин служат для характеристики изменения уровня явления, отнесенного к единице совокупности, например: данные о среднегодовой численности занятых в экономике; о средней урожайности отдельных сельскохозяйственных культур, о средней заработной плате в отдельных отраслях и т.д.
В зависимости от характера временного параметра ряды динамики делятся на моментные и интервальные.
Уровни моментных рядов динамики характеризуют явление по состоянию на определенный момент времени.
Пример. Моментный ряд динамики, характеризующий численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г., представлен в таблице 13.1.
Таблица 13.1 ‑ Численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г
| Дата | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 |
| Численность персонала, чел. | 780 | 810 | 880 | 930 | 940 | 970 |
Следует помнить, что моментные ряды абсолютных величин нельзя суммировать. Бессмысленно, например, складывать численность персонала по состоянию на 1 января, 1 февраля и т.д. Полученная сумма ничего не выражает, так как в ней многократно повторяются одни и те же единицы совокупности.
Ряд, в котором уровни характеризуют результат, накопленный или вновь произведенный за определенный интервал времени, называется интервальным.
Пример. Интервальный ряд динамики, представлен в таблице 13.2.
Таблица 13.2. ‑ Характеристика динамики объема розничного товарооборота
| Дата | 2004 | 2005 | 2006 | 2007 | 2008 |
| Товарооборот, млн. руб. | 28,3 | 31,9 | 38,3 | 42,3 | 45,2 |
Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда вполне реальный показатель, например, общий объем розничного товарооборота за 2004-2008 г.г.
В зависимости от расстояния между уровнями, ряды динамики подразделяются на ряды с равноотстоящими уровнями и не равноотстоящими уровнями во времени.
Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называются равноотстоящими, пример (табл. 13.1 и табл. 13.2).
Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются не равноотстоящими, пример(табл. 13.3).
Пример. Рядом динамики с не равноотстоящими уровнями во времени может служить объем экспорта продукции предприятия, представленный в таблице 13.3.
Таблица 13.3. – Динамика объема экспорта продукции предприятия
| Годы | 1993 | 1996 | 1998 | 2000 | 2004 |
| Объем экспорта, млн. долл. | 1110 | 1220 | 1320 | 1450 | 1640 |
По числу показателей можно выделить изолированные (одномерные) и комплексные (многомерные) ряды динамики.
Если ведется анализ во времени одного показателя ряда, то ряд динамики изолированный (например, данные о производстве газа по годам). В многомерном ряду представлена динамика нескольких показателей, характеризующих одно явление.
Сопоставимость уровней и смыкание рядов динамики
Важнейшим условием правильного построения рядов динамики является сопоставимость всех входящих в него уровней. Данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.
Рассмотрим основные причины несопоставимости уровней ряда динамики.
Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения и единиц счета.
Пример. Нельзя сравнивать и анализировать цифры о производстве тканей, если за одни годы оно дано в погонных метрах, а за другие ‑ в квадратных метрах.
На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей.
Например, если в одни годы среднюю урожайность считали с засеянной площади, а в другие ‑ с убранной, то такие уровни будут несопоставимы.
В процессе развития во времени, прежде всего, происходят количественные измерения явлений, а затем на определенных ступенях совершаются качественные скачки, приводящие к изменению закономерностей явления. Поэтому научный подход к изучению рядов динамики заключается в том, чтобы ряды, охватывающие большие периоды времени, разделять на такие, которые бы объединяли лишь однокачественные периоды развития совокупности, характеризующейся одной закономерностью развития.
Важно также, чтобы в ряду динамики интервалы или моменты, по которым определены уровни, имели одинаковый экономический смысл.
Например, при изучении роста поголовья скота бессмысленно сравнивать цифры поголовья по состоянию на 1 октября с данными 1 января, так как первая цифра включает не только скот, оставшийся на зимовку, но и предназначенный к убою, а вторая цифра включает только скот, оставленный на зимовку. Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое.
Несопоставимость уровней ряда может возникнуть вследствие изменений территориальных границ областей, районов и так далее.
Для того, чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который носит название смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых являются несопоставимыми. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).
Пример. Предположим, что в N-ом регионе имеются данные об общем объеме оборота розничной торговли за 2013-2015 гг. в фактически действующих ценах, и за 2015-2018 гг. ‑ в сопоставимых ценах (табл. 13.4.).
Таблица 13.4 ‑ Динамика общего объема оборота розничной торговли (млрд. руб.) цифры условные
|
Годы |
2013 | 2014 | 2015 | 2016 | 2017 |
2018 |
|
Оборот розничной торговли, млрд. руб. (в фактически действующих ценах) |
19,7 | 20 | 21,2 | |||
| Оборот розничной торговли, млрд. руб. (в сопоставимых ценах) | 22,8 | 24,6 | 25,2 |
26,1 |
||
| Сомкнутый ряд абсолютных величин (в сопоставимых ценах; млрд. руб.) |
21,3 |
21,5 | 22,8 | 24,6 | 25,2 |
26,1 |
| Сопоставимый ряд относительных величин (в % к 2005 г.) |
92,9 |
94,3 | 100 | 107,9 | 110,5 |
114,5 |
Решение. Чтобы проанализировать динамику общего объема розничной торговли за 2013-2018 гг., необходимо сомкнуть (объединить) приведенные выше два ряда в один. А чтобы уровни нового ряда были сопоставимы, необходимо пересчитать данные 2003-2005 гг. в сопоставимые цены. Для этого на основе данных об объеме розничной торговли за 2005 г. в фактических и сопоставимых ценах находим соотношение между ними: 22,8:21,2 = 1,08. Умножая на полученный коэффициент данные за 2003-2005 гг., приводим их, таким образом, к сопоставимому виду с последующими уровнями. Сомкнутый (сопоставимый) ряд динамики показан в предпоследней строке таблицы 13.4.
Другой способ смыкания рядов заключается в том, что уровни года, в котором произошли изменения (в нашем примере ‑ уровни 2005 г.), как до изменений, так и после изменений (для нашего примера ‑ в фактических и сопоставимых ценах, т.е. 21,2 и 22,8) принимаются за 100%, а остальные пересчитываются в процентах по отношению к этим уровням соответственно (в нашем примере в фактических ценах ‑ по отношению к 21,2, в сопоставимых ценах ‑ к 22,8). В результате получаем сомкнутый ряд динамики, который показан в последней строке таблицы 13.4.
Та же проблема приведения к сопоставимому виду возникает и при параллельном анализе развития во времени экономических показателей отдельных стран, административных и территориальных районов. Это, во-первых, вопрос о сопоставимости цен сравниваемых стран, во-вторых, вопрос о сопоставимости методики расчета сравниваемых показателей. В таких случаях ряды динамики приводятся к одному основанию, то есть к одному и тому же периоду или моменту времени, уровень которого принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.
Аналитические показатели ряда динамики
На практике для количественной оценки динамики явлений широко применяется ряд основных аналитических показателей. К таким показателям относятся, абсолютный прирост при этом принято сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение – базисным.
Абсолютный прирост (∆y ) характеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста.
∆y – абсолютный прирост – это разность между уровнями ряда динамики. Может быть цепным или базисным:
(13.1) – абсолютный прирост цепной
(13.2)- абсолютный прирост базисный
Показатель интенсивности изменения уровня ряда ‑ в зависимости от того, выражается ли он в виде коэффициента или в процентах, принято называть коэффициентом роста или темпом роста.
Коэффициент роста показывает, во сколько раз данный уровень ряда больше базисного уровня (если этот коэффициент больше единицы) или какую часть базисного уровня составляет уровень текущего периода за некоторый промежуток времени (если он меньше единицы).
Тр– темп роста – относительный показатель, получающийся в результате сопоставления двух уровней одного ряда динамики. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем:
(13.3) – темп роста цепной
либо как базисные, когда все уровни сопоставляются с одним и тем же уровнем, выбранным за базу сравнения (при умножении на 100 – в процентном выражении):
(13.4) – темп роста базисный
Между цепными и базисными темпами роста существует взаимосвязь: произведение всех цепных темпов роста равно последнему базисному.
Т пр – темп прироста – относительный показатель, показывающий, насколько один уровень ряда динамики больше или меньше другого, принимаемого за базу сравнения:
(13.5)
При делении абсолютного прироста (цепного) на темп прироста (цепной) получим показатель, называемый значением одного процента прироста – А:
(13.6)- значение одного процента прироста
Пример. Произведем расчет и анализ динамики заключения браков в Омской области за 2000–2003 гг., используя формулы вышеизложенных показателей и данные табл. 13.5. За базу сравнения примем уровень 2000 года.
Таблица 13.5 – Показатели изменения уровней ряда динамики
|
Показатели |
Год | |||
| 2000 | 2001 | 2002 |
2003 |
|
|
Заключение браков, единиц |
13277 | 15130 | 15880 |
16458 |
Абсолютные приросты, ∆y
Далее в табл. 13.6 приведем всю совокупность показателей ряда динамики, позволяющую посмотреть взаимосвязи между ними.
Таблица 13.6 – Показатели изменения уровней ряда динамики
| Показатели | Год | |||
| 2000 | 2001 | 2002 | 2003 | |
| 1. Заключение браков, единиц | 13277 | 15130 | 15880 | 16458 |
| 2. Темпы роста базисные: | − | 1,14 | 1,196 | 1,24 |
| 2.1. коэффициенты | ||||
| 2.2. проценты | − | 114 | 119,6 | 124 |
| 3. Темпы роста цепные: | − | 1,14 | 1,05 | 1,036 |
| 3.1. коэффициенты | ||||
| 3.2. проценты | − | 114 | 105 | 103,6 |
| 4. Абсолютные приросты, ед. | − | 1853 | 2603 | 3181 |
| 4.1. базисные (2000 г.) | ||||
| 4.2. цепные (по годам) | − | 1853 | 750 | 578 |
| 5. Темпы прироста базисные | − | 0,14 | 0,196 | 0,24 |
| 5.1. коэффициенты | ||||
| 5.2. проценты | − | 14 | 19,6 | 24 |
| 6. Темпы прироста цепные | − | 0,14 | 0,05 | 0,036 |
| 6.1. коэффициенты | ||||
| 6.2. проценты | − | 14 | 5 | 3,6 |
| 7. Абсолютное значение 1 % пр. | − | 132,36 | 150 | 160,6 |
При изучении ряда динамики важно проследить за направлением и размером изменений уровня ряда во времени. С этой целью для динамических рядов рассчитываются следующие показатели.
Среднегодовой темп роста, ориентированный на достижение конечного уровня (yn) в исследуемом периоде, можно рассчитать как среднюю геометрическую из годовых темпов роста по следующим формулам:
(13.7)
Если же ориентация берется на достижение суммарного значения (объема) исследуемого показателя за определенный период, то для расчета среднего коэффициента (темпа) роста используется так называемая средняя параболическая вида
(13.8)
где значение k определяется по специальной таблице для расчета средних коэффициентов роста (снижения) по средней параболической.
Пример. Таблица 13.7 – Данные о вводе в действие жилой площади в городе N
| Год | 2002 | 2003-2008 |
| Введено млн. кв. м общей площади, уi | 62,5 | 394,7 |
Определим среднегодовой темп роста ввода в действие жилой площади за 2003‑2008 гг. (т.е. за 6 лет), ориентированный на достижение общей суммы введенного жилья за указанный период (т.е. 394, 7 млн. кв.м).
Решение. Используем формулу (13.8) средней параболической:
далее по таблице для расчета средних коэффициентов роста (снижения) по средней параболической в графе n=6 находим значение, наиболее близкое к полученному отношению (6,315). Это число 6,323, которому соответствует =1,015. Это искомый среднегодовой коэффициент роста ввода жилья за 6 лет. Отсюда, среднегодовой темп роста ввода в действие жилой площади за указанный период составлял 101,5%, а среднегодовой темп прироста был равен 101,5% ‑ 100% =1,5%.
Пример. Таблица 13.8 – Данные о прибыли на предприятии за 2000‑2005 гг.
| Год | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| Валовая прибыль, млн руб. | 566 | 521 | 447 | 428 | 391 | 367 |
Рассчитаем среднегодовой темп роста(снижения) за 2000‑2005 гг., ориентированный:
- достижение фактического уровня в 2005 г. по формуле (13.7)
или 91,7%, т.е. ежегодно объем прибыли уменьшался в среднем на 8,3%;
- если при расчете ориентироваться на общий объем, за 5 лет, то применим для расчета формулу (13.8):
Пример. Имеются данные о численности мужской части населения Омской области за 5 лет на начало года (табл. 10.11):
далее по таблице =0,91, т.е. среднегодовое снижение прибыли при общем объеме за 5 лет составило 9%.
На практике, т.к конечный уровень ряда может быть случайным(нехарактерным), чаще применяется расчет по формуле (13.8), где учитывается сумма уровней за n лет.
Прогнозирование на основе рядов динамики
Суть нижеприведенного способа (выравнивание по аналитическим формулам) заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени, т.е.
Таблица 13.9 – Численность мужской части населения в 1999–2003 гг. (на 1.01.),
| Год | 1999 | 2000 | 2001 | 2002 | 2003 |
| Численность
тыс. чел. |
1028,8 | 1020,1 | 1010,7 | 999,6 | 989,8 |
Найдем линию тренда и, используя полученное уравнение, сделаем прогноз на будущее (определим численность мужской части населения в Омской области в 2006 году).
Предположим, что численность населения изменяется во времени по прямой:
(13.9)
Для нахождения параметров а0 и а1 решим систему нормальных уравнений, отвечающих требованию способа наименьших квадратов
(13.10)
Далее в табл. 10.12 рассчитаны необходимые для решения системы уравнения суммы: ∑, ∑t, ∑t2, ∑yt. Годы последовательно обозначим как 1, 2, 3, 4, 5 (n=5).
Таблица 13.10 – Расчетные данные для определения параметров уравнения тренда
| Год | Число мужчин, тыс. чел. yi | Условное обозначение времени, t | t2 | y·t | Уравнение тренда |
| 1999 | 1028,8 | 1 | 1 | 1028,8 | 1029,5 |
| 2000 | 1020,1 | 2 | 4 | 2040,2 | 1019,65 |
| 2001 | 1010,7 | 3 | 9 | 3032,1 | 1009,8 |
| 2002 | 999,6 | 4 | 16 | 3998,4 | 999,95 |
| 2003 | 989,8 | 5 | 25 | 4949 | 990,1 |
| ∑ | 5049 | 15 | 55 | 15048,5 | 5049 |
Из системы уравнений получим a1 = −9,85; а0 = 1039,35;
Отсюда искомое уравнение тренда
Для 2006 года t = 8; следовательно, То есть по прогнозу численность мужской части населения в Омской области в 2006 году составит 960,55 тыс. чел.
Для решения данной задачи можно использовать и второй способ, упрощенный. Если время t обозначить так, чтобы ∑t = 0, т.е. счет вести от середины ряда, то система упростится и примет вид
(13.11)
В этом случае каждое уравнение решается самостоятельно:
(13.12)
(13.13)
Необходимые для расчета параметров уравнения суммы приведем в табл. 10.13.
Таблица 13.11 – Расчетные данные для определения параметров уравнения тренда
| Год | Число мужчин, тыс. чел. yi | Условное обозначение времени, t | t2 | yt | Уравнение тренда |
| 1999 | 1028,8 | -2 | 4 | -2058 | 1029,5 |
| 2000 | 1020,1 | -1 | 1 | -1020 | 1019,65 |
| 2001 | 1010,7 | 0 | 0 | 0 | 1009,8 |
| 2002 | 999,6 | 1 | 1 | 999,6 | 999,95 |
| 2003 | 989,8 | 2 | 4 | 1979,6 | 990,1 |
| Итого | 5049 | 0 | 10 | -98,5 | 5049 |
Тогда и
Уравнение тренда в этом случае будет имеет вид
Для 2006 г. t = 5; следовательно,
Эта величина условная, рассчитанная при предположении, что линейная закономерность изменения численности мужской части населения, принятая для 1999–2003 гг., сохранится на последующий период до 2006 г.
Контрольные задания.
По данным статистических ежегодных изданий: «Российский статистический ежегодник», «Россия в цифрах» и т.п. выберите несколько показателей, постройте и проанализируйте ряды динамики, найдите линию тренда и, используя полученное уравнение, сделайте прогноз на 3 года вперед.
АНОНС…полный текст будет опубликован позднее… в соответствии с графиком занятий
Содержание курса лекций «Статистика»









