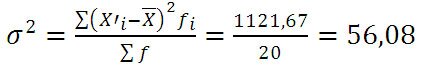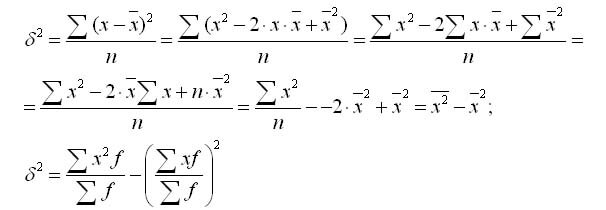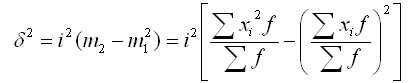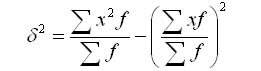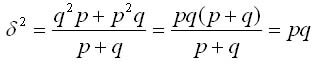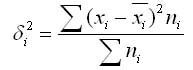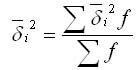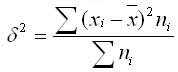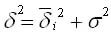Дисперсия как найти два способа

Как найти дисперсию?

Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).

Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.

Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).

Формула дисперсии случайной величины

Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$

Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.

Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$

Пример нахождения дисперсии

Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.

Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$

Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.

Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).

Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$

Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.

Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.

Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.

Другие задачи с решениями по ТВ

Вычисление дисперсии онлайн

Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.

• Введите число значений случайной величины К.
• Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
• Нажмите на кнопку “Вычислить”.
• Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.

Видео. Полезные ссылки

Видеоролики: что такое дисперсия и как найти дисперсию

Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Полезные ссылки

Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.

Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

В
большинстве случаев математическое
ожидание еще не достаточно характеризует
случайную величину. На практике
встречаются случайные величины, имеющие
одинаковые математические ожидания,
однако принимающие резко различающиеся
значения. У одних из этих величин
отклонения значений от математического
ожидания небольшие, а для других,
наоборот, значительны, т.е. для одних
рассеивание значений случайной величины
вокруг математического ожидания мало,
а для других оно велико.

Например,
пусть случайные величины X
и Y
заданы следующими законами распределения:

X	–0,1	–0,01	0	0,01	0,1		Y	–20	–10	0	10	20
P	0,1	0,2	0,4	0,2	0,1		P	0,3	0,1	0,2	0,1	0,3

Математические
ожидания этих случайных величин одинаковы
и равны нулю. Однако характер их
распределения их различный. Случайная
величина X
принимает значения, мало отличающиеся
от математического ожидания, а случайная
величина Y
– значения, значительно отличаются от
математического ожидания.

Приведенные
рассуждения и пример свидетельствую о
целесообразности введения такой
характеристики случайной величины,
которая оценивала бы меру рассеивания
значений случайной величины вокруг ее
математического ожидания, тем более
что на практике часто приходится
оценивать такое рассеивание. Например,
артиллеристам необходимо знать как
кучно лягут снаряды вблизи цели, по
которой ведется стрельба.

На
первый взгляд может показаться, что для
оценки рассеяния проще всего вычислить
все возможные значения отклонения
случайной величины и затем найти их
среднее значение. Однако такой путь
ничего не дает, т.к. среднее значение
отклонение для любой случайной величины
равно нулю. Это объясняется тем, что
возможные значения X–M[X]
могут иметь как положительные, так и
отрицательные знаки.

Избежать
изменения знаков отклонений x_i–
M[X]
можно, если заменить их абсолютными
значениями или возвести в квадрат.
Замена отклонений их абсолютными
величинами нецелесообразно, т.к. действия
с абсолютными величинами, как правило,
вызывают затруднения. Поэтому следует
использовать величину (X–M[X])²
(точнее, ее среднее значение) для
характеристики рассеивания значений
случайной величины.

Определение.
Дисперсией
(рассеянием) случайной величины называют
математическое ожидание квадрата
отклонения случайной величины от ее
математического ожидания:

.
(5.4)

Законы
распределения вероятностей случайной
величины X
и (X–M[X])²
одинаковы. Пусть M[X]m,
тогда дисперсия ДСВ будет иметь вид

,
(5.5)

дисперсия НСВ

дисперсия
.
(5.6)

Из
определения следует, что дисперсия
случайной величины есть величина не
случайная (постоянная). Тогда формулу
для дисперсии можно преобразовать
следующим образом

Таким образом,

.
(5.7)

Это есть основная
формула для вычисления дисперсии.

Случайная
величина и ее математическое ожидание
имеют одну и ту же размерность, но
дисперсия имеет размерность квадрата
случайной величины. недостатка можно
избежать если воспользоваться величиной,
равной квадратному корню из дисперсии:

.
(5.8)

Эта
случайная величина называется средним
квадратичным отклонением
случайной величиной.

Пример
5.4. ДСВ
X
задана следующим законом распределения:

X	2	3	4
P	0,3	0,4	0,3

Найти
дисперсию D[X]
двумя способами и среднее квадратичное
отклонение.

Решение.
Способ 1.

Способ 2.

Среднее квадратичное
отклонение

Пример
5.5. НСВ
X
задана следующей плотностью распределения:

Найти
дисперсию D[X]
двумя способами и среднее квадратичное
отклонение.

Решение.
Способ 1.

Способ 2.

,

Среднее квадратичное
отклонение

Отметим
некоторые свойства дисперсии.

Свойство
1.
Дисперсия
постоянной величины равно нулю:

D[C]
= 0.

Действительно,
т.к. M[С]=C,
то D[C]=M[С–M(С)]²=M[С–С]²=M[0]=0.
Это свойство очевидно, т.к. постоянная
величина принимает только одно значение,
следовательно, рассеяние рассеяния
вокруг математического ожидания нет.

Свойство
2.
Постоянный
множитель можно выносить за знак
дисперсии, возводя его в квадрат:

D[CX]
= C²
D[X].

Действительно,
т.к. постоянный множитель можно выносить
за знак математического ожидания, то

Свойство
3. Дисперсия
суммы двух независимых случайных величин
равно сумме дисперсий этих величин:

D[X+Y]
= D[X]+
D[Y].

Действительно,
учитывая свойства математического
ожидания, получим

Свойство
4.
Дисперсия
разности двух независимых случайных
величин равно сумме их дисперсий:

D[X–Y]
= D[X]
+ D[Y].

Действительно,
в силу свойства 3 D[X–Y]
= D[X]
+ D[–Y].
В соответствие со свойством 2, получим

Ранее было введено
понятие отклонения случайной величины
от ее математического ожидания. Эту
случайную величину

X–M[X]

Иногда
называют центрированной
случайной величиной.
Выше было показано (свойство 5), что
математическое ожидание случайной
величины равно нулю. Найдем дисперсию
центрированной случайной величины. На
основании свойств дисперсии, получим

Таким
образом, дисперсия
случайной величины X
и центрированной случайной величины
X–M[X]
равны
между собой.

Иногда
бывает удобно использовать безразмерные
центрированные случайные величины.
Разделим величину X–M[X]
на среднее квадратичное отклонениеsимеющее ту же размерность. Вновь
полученную случайную величину называютстандартной случайной
величиной:

.
(5.9)

Стандартная
случайная величина обладает следующими
свойствами: 1) M[Z]=0,
2) D[X]=1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

2.2.5. Формула для вычисления дисперсии

Данная формула выводится непосредственно из определения дисперсии, и мы незамедлительно пускаем её в оборот. Скопирую сверху табличку с нашей игрой:

и найденное матожидание .

Вычислим дисперсию вторым способом. Сначала найдём математическое ожидание – квадрата случайной величины . По определению математического ожидания, значения случайной величины следует перемножить на соответствующие вероятности и эти произведения сложить:

в данном случае:

Таким образом, по формуле:

Как говорится, почувствуйте разницу. И на практике, конечно, лучше применять формулу (если иного не требует условие).

Осваиваем технику решения и оформления:

Задача 87
Дискретная случайная величина задана своим законом распределения:

Найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.

Эта задача встречается повсеместно, и, как правило, идёт без содержательного смысла. Но желающие могут представить четыре лампочки с числами, которые загораются в дурдоме с определёнными вероятностями 🙂

Решение: Основные вычисления удобно свести в таблицу. Сначала в верхние две строки записываем исходные данные. Затем рассчитываем произведения , затем и, наконец, суммы в правом столбце:

Собственно, почти всё готово. В третьей строке нарисовалось готовенькое математическое ожидание: .

Дисперсию вычислим по формуле:

И, наконец, среднее квадратическое отклонение:
– лично я обычно округляю результат до 2 знаков после запятой.

Все вычисления можно провести на калькуляторе, а ещё лучше – в Экселе (ссылка на видеоролик на Ютубе). Вот здесь вот уже будет трудно ошибиться.

Ответ:

Пара заданий для самостоятельного решения:

Задача 88
Вычислить дисперсию случайной величины предыдущего примера по определению.

…встречается и такая задача, я ничего не придумываю. Почти J

И аналогичный пример:

Задача 89
Дискретная случайная величина задана своим законом распределения:

Найти

Да, значения случайной величины бывают достаточно большими, и здесь по возможности лучше использовать Эксель.

И в заключение параграфа разберём ещё одну типовую задачу, можно даже сказать, небольшой ребус:

Задача 90
Дискретная случайная величина может принимать только два значения: и , причём . Известна вероятность , математическое ожидание и дисперсия .

Найти .

Решение: начнём с неизвестной вероятности. Так как случайная величина может принять только два значения, то сумма вероятностей соответствующих событий:

и поскольку , то .

Осталось найти …, легко сказать 🙂 Но да ладно, понеслось. По определению математического ожидания:
– подставляем известные величины:

– и больше из этого уравнения ничего не выжать, разве что можно переписать его в привычном направлении:

ОК, едем дальше. По формуле вычисления дисперсии:
– подставляем известные данные:

и реверанс:
О дальнейших действиях, думаю, вы догадываетесь. Составим и решим систему:

Десятичные дроби – это, конечно, безобразие, умножаем оба уравнения на 5:

Вот так-то лучше. Из 1-го уравнения выражаем:
(это более простой путь) – подставляем во 2-е уравнение:

Возводим разность в квадрат и проводим упрощения:

В результате получено квадратное уравнение, находим его дискриминант:
и извлекаем из него корень:
– отлично, целое значение, значит, мы на верном пути.

Таким образом, у нас получаются два решения:

1) если , то ;

2) если , то .

Условию удовлетворяет первая пара корней. С высокой вероятностью всё правильно, но, тем не менее, запишем закон распределения:

и выполним проверку, а именно, найдём матожидание:

и дисперсию:

В результате получены исходные значения, что и требовалось проверить.

Ответ: …да, вроде бы такие простенькие числа, но вычисления…, и поэтому в этой задаче следует проявлять повышенное внимание.

Переходим к графическому представлению дискретной случайной величины:

Полную и свежую версию этой книги в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Дисперсия, виды и свойства дисперсии

Понятие дисперсии

Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:

2. Взвешенная дисперсия (для вариационного ряда):

где n — частота (повторяемость фактора Х)

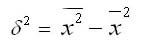
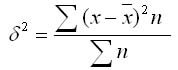
Пример нахождения дисперсии

На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение

Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию

Построим интервальную группировку. Определим размах интервала по формуле:

где X max– максимальное значение группировочного признака;
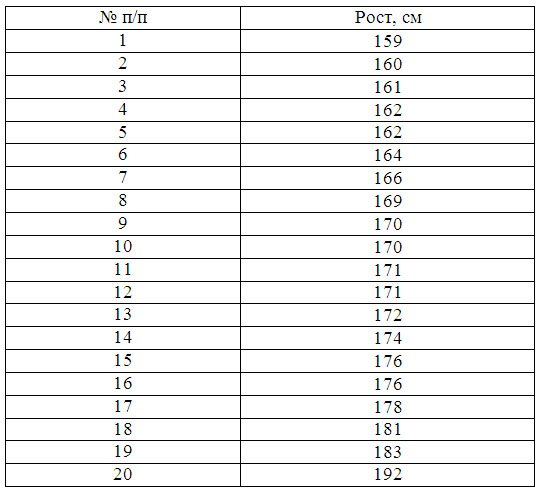
X min–минимальное значение группировочного признака;
n – количество интервалов:

Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6

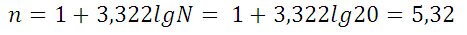
Составим интервальную группировку

Для дальнейших расчетов построим вспомогательную таблицу:

X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)

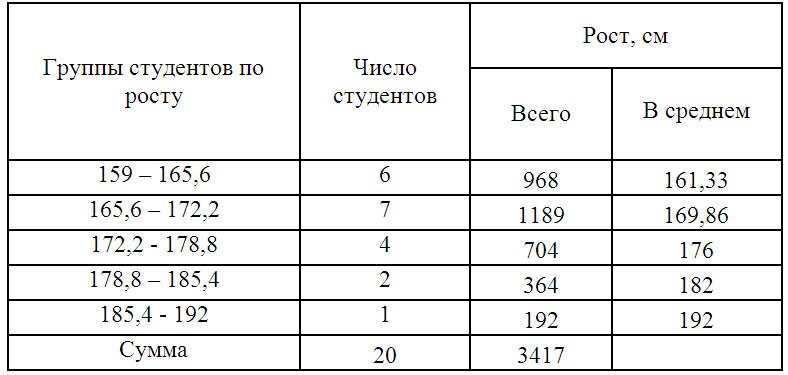
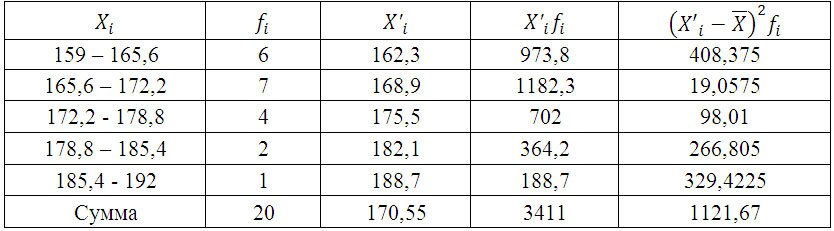
Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:

Определим дисперсию по формуле:

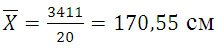
Формулу дисперсии можно преобразовать так:

Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.

Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:

где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка

Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:

Подставляя в данную формулу дисперсии q =1- р, получаем:

Виды дисперсии

Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.

Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.

Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:

где хi — групповая средняя;
ni — число единиц в группе.

Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).

Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:

Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:

Правило сложения дисперсии в статистике

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.

Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.

Свойства дисперсии

1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.

Источник

Была ли эта статья полезной?