Как найти дисперсию?
Спасибо за ваши закладки и рекомендации
Дисперсия – это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая – значения сравнительно близки друг к другу, если большая – далеки друг от друга (см. примеры нахождения дисперсии ниже).
Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии – среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.
Еще одно формальное определение дисперсии звучит так: “Дисперсия – это второй центральный момент случайной величины” (напомним, что первый начальный момент – это как раз математическое ожидание).
Нужна помощь? Решаем теорию вероятностей на отлично
Формула дисперсии случайной величины
Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$
Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.
Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Пример нахождения дисперсии
Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.
Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$
Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором – дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 – (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 – (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором – на 10 единиц от среднего 0.
Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).
Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.
Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.
Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx – left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.
Другие задачи с решениями по ТВ
Подробно решим ваши задачи на вычисление дисперсии
Вычисление дисперсии онлайн
Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.
Видео. Полезные ссылки
Видеоролики: что такое дисперсия и как найти дисперсию
Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Понравилось? Добавьте в закладки
Полезные ссылки
Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по ТВ. Для закрепления материала – еще примеры решений задач по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Дискретные распределения вероятностей и их параметры
- Общие свойства дискретного распределения
- Функция распределения дискретной случайной величины
- Числовые характеристики дискретного распределения
- Таблица дискретных распределений, их параметров и числовых характеристик
- Примеры
п.1. Общие свойства дискретного распределения
Величина, которая в результате испытания может принимать то или иное числовое значение, называется случайной величиной.
Случайная величина называется дискретной, если она принимает не более чем счетное количество значений.
Дискретная случайная величина называется конечной, если она принимает конечное число значений.
Согласно данному определению дискретная величина может быть определена либо на бесконечном счетном множестве, либо на конечном множестве (которое всегда счетное).
Напомним, что счетным называется множество, которое эквивалентно множеству натуральных чисел, т.е. элементы которого можно пронумеровать (см. §11 справочника для 8 класса).
Например:
1) При подбрасывании игрального кубика мы получаем всего 6 исходов. Случайная величина X – выпавшее число очков – принимает конечное число значений (Omega=left{1;2;3;4;5;6right}), т.е. является дискретной конечной случайной величиной.
2) Случайная величина X – количество поступивших вызовов на сервер за сутки – не ограничена сверху и может принимать значения (Omega=left{1;2;3;…right})
Правило, устанавливающее связь между значениями случайной величины и вероятностью получения каждого из этих значений в испытании, называется законом распределения.
Случайная величина полностью описывается своим законом распределения.
Закон распределения может быть задан аналитически (формулой), таблично или графически.
Закон распределения конечной дискретной случайной величины, заданный в виде таблицы, называют рядом распределения.
Например:
В результате измерения температуры учеников школы получен следующий ряд распределения:
| t, °C | 36,3 | 36,4 | 36,5 | 36,6 | 36,7 | 36,8 | 36,9 | 37,0 | 37,1 |
| p(t) | 0,05 | 0,07 | 0,15 | 0,33 | 0,31 | 0,11 | 0,04 | 0,01 | 0,01 |
Значения (left{x_1,x_2,…,x_kright}), которые может принимать конечная случайная величина X, являются несовместными и образуют полную группу событий. Сумма их вероятностей: $$ sum_{i=1}^k p_i=1, p_igeq 0 $$
Чтобы вспомнить о несовместных событиях и полной группе событий – см. §39 справочника для 9 класса.
Например:
Пусть в урне находится 2 белых и 3 черных шара. Мы достаем шар, смотрим на его цвет, возвращаем его обратно и все шары перемешиваем. Таким образом, событие A=«достали белый шар» каждый раз является независимым от предыдущих и имеет вероятность (p=frac25).
Пусть мы провели n=3 испытания. В 3 испытаниях можно получить от 0 до 3 белых шаров. Вероятность событий (kinleft{0;1;2;3right}) описывается биномиальным законом распределения (см. §40 справочника для 9 класса): $$ P_3(k)=C_3^k p^k q^{3-q}, k=overline{0;3} $$ Получаем закон распределения: begin{gather*} P_3(0)=C_3^0 p^0 q^{3-0}=q^3=left(frac35right)^3=frac{27}{125}\ P_3(1)=C_3^1 p^1 q^{3-1}=3pq^2=3cdot frac25cdot left(frac35right)^2=frac{54}{125}\ P_3(2)=C_3^2 p^2 q^{3-2}=3p^2q=3cdot left(frac25right)^2cdot frac35=frac{36}{125}\ P_3(3)=C_3^3 p^3 q^{3-3}=p^3=left(frac25right)^3=frac{8}{125} end{gather*}
| k | 0 | 1 | 2 | 3 |
| (P_3(k)) | (frac{27}{125}) | (frac{54}{125}) | (frac{36}{125}) | (frac{8}{125}) |
Сумма вероятностей: $$ sum_{k=0}^3 P(k)=frac{27+54+36+8}{125}=1 $$
п.2. Функция распределения дискретной случайной величины
Функцией распределения дискретной случайной величины называют функцию, которая определяет вероятность, что значение случайной величины X не превышает граничное значение x: $$ F(x)=P(Xleq x) $$
Для дискретной случайной величины функция распределения будет ступенчатой кусочно-непрерывной функцией, область значений которой: (F(x)in[0;1]).
Слева на графике функции распределения будет нулевая «ступенька», а справа – единичная «ступенька».
Например:
Найдем из закона распределения случайной величины k, полученного в предыдущем примере для урны с шарами, функцию распределения.
| k | 0 | 1 | 2 | 3 |
| (P_3(k)) | (frac{27}{125}) | (frac{54}{125}) | (frac{36}{125}) | (frac{8}{125}) |
| (F(k)) | (frac{27}{125}) | (frac{27+54}{125}=frac{81}{125}) | (frac{81+36}{125}=frac{117}{125}) | (frac{117+8}{125}=1) |
Изобразим графически закон распределения в виде гистограммы:
Построим график для функции распределения: begin{gather*} F(k)= begin{cases} 0, kleq 0\ frac{27}{125}, 0lt kleq 1\ frac{81}{125}, 1lt klt 2\ frac{117}{125}, 2lt kleq 3\ 1, kgt 3 end{cases} end{gather*} 
п.3. Числовые характеристики дискретного распределения
Числовыми характеристиками дискретного распределения являются математическое ожидание, дисперсия и среднее квадратичное отклонение (СКО).
Подробно о свойствах этих характеристик – см. §41 справочника для 9 класса.
Здесь мы приведем только основные определения.
Математическое ожидание дискретной случайной величины X = {xi} равно сумме произведений всех возможных значений xi на соответствующие вероятности pi: $$ M(X)=x_1p_1+x_2p_2+…+x_{n}p_{n}=sum_{i=1}^n x_{i}p_{i} $$ Математическое ожидание является средним значением величины X.
Дисперсия дискретной случайной величины X = {xi} – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания: $$ D(X)=M(X-M(X))^2 $$ На практике дисперсия рассчитывается по формуле: $$ D(X)=M(X)^2-M^2(X)=sum_{i=1}^n x_i^2p_i-M^2(X) $$
Среднее квадратичное отклонение (СКО) дискретной случайной величины X = {xi} – это корень квадратный от дисперсии: $$ sigma(X)=sqrt{D(X)} $$ СКО характеризует степень отклонения случайной величины от среднего значения.
Например:
Рассчитаем числовые характеристики для урны с шарами из предыдущего примера.
Составим расчетную таблицу:
| (x_i) | 0 | 1 | 2 | 3 | ∑ |
| (p_i) | (frac{27}{125}) | (frac{54}{125}) | (frac{36}{125}) | (frac{8}{125}) | (1) |
| (x_i p_i) | (0) | (frac{54}{125}) | (frac{72}{125}) | (frac{24}{125}) | (1,2) |
| (x_i^2) | 0 | 1 | 4 | 9 | – |
| (x_i^2 p_i) | (0) | (frac{54}{125}) | (frac{144}{125}) | (frac{72}{125}) | (2,16) |
Получаем begin{gather*} M(X)=sum_{i=0}^3 x_i p_i=1,2=frac65\ D(X)=sum_{i=0}^3 x_i^2 p_i-M^2(X)=2,16-1,2^2=0,72=frac{18}{25}\ sigma(X)=sqrt{D(X)}=sqrt{frac{18}{25}}=frac{3sqrt{2}}{5} end{gather*} В научных статьях и технической документации принято записывать случайные величины в виде (x=M(X)pmsigma (X)).
В данном случае для числа вынутых белых шаров в 3 испытаниях можем записать: $$ k=frac{6pm 3sqrt{2}}{5} $$
п.4. Таблица дискретных распределений и их параметров
| Название | Принятое обозначение |
Плотность распределения |
Мат. ожидание |
Дисперсия |
| Дискретное равномерное | (U(N)) | begin{gather*} P(left{kright})=frac1N\ Ninmathbb{N}, kinleft{1,…,Nright} end{gather*} | (frac{N+1}{2}) | (frac{N^2-1}{12}) |
| Бернулли | (B(1,p)) | begin{gather*} P(0)=1-p=q\ P(1)=p\ kinleft{0;1right} end{gather*} | (p) | (pq) |
| Биномиальное | (B(n,p)) | begin{gather*} P(left{kright})=C_n^k p^k q^{n-k}\ ninmathbb{N}, k=inleft{0,1,…,nright} end{gather*} | (np) | (npq) |
| Пуассона | (Pois(lambda)) | begin{gather*} P(left{kright})=frac{lambda^k}{k!}e^{-lambda}\ lambdagt 0, k=inleft{0,1,…,nright} end{gather*} | (lambda) | (lambda) |
| Геометрическое | (Geopm(p)) | begin{gather*} P(left{kright})=pq^{k-1}\ k=inleft{0,1,2,…right} end{gather*} | (frac1p) | (frac{q}{p^2}) |
| Гипер-геометрическое | (HG(D,N,n)) | begin{gather*} P(left{kright})=frac{C_D^k C_{N_D}^{n-k}}{C_N^n} end{gather*} | (frac{nD}{N}) | $$frac{frac{nD}{N}left(1-frac DNright)(N-n)}{N-1}$$ |
п.5. Примеры
Пример 1. Выведите формулы для мат.ожидания и дисперсии дискретного равномерного распределения
Случайная величина имеет дискретное равномерное распределение, если она принимает конечное число N значений с равными вероятностями. Значения исходов (k_iinleft{1,…,Nright}). Вероятность каждого из исходов (p_i=frac1N, i=overline{1,N}).
Предварительно заметим, что по формуле суммы арифметической прогрессии: $$ sum_{i=1}^N k_i=1+2+…+N=frac{N(N+1)}{2} $$ А сумму квадратов можно найти по формуле Архимеда (доказательство – см. пример 2 в §25 справочника для 9 класса): $$ sum_{i=1}^N k_i^2=1^2+2^2+…+N^2=frac{N(N+1)(2N+1)}{6} $$ Найдем математическое ожидание: $$ M(X)=sum_{i=1}^N k_ip_i=sum_{i=1}^N k_icdot frac1N=frac1N(1+2+…+N)=frac1Ncdotfrac{N(N+1)}{2}=frac{N+1}{2} $$ Найдем дисперсию: begin{gather*} D(X)=sum_{i=1}^N k_i^2 p_i-M^2(X)=sum_{i=1}^N k_i^2cdotfrac1N-M^2(X)=\ =frac1Ncdotfrac{N(N+1)(2N_1)}{6}-left(frac{N+1}{2}right)^2=frac{(N+1)(2N+1)}{6}-frac{(N+1)^2}{4}=\ =frac{N+1}{2}left(frac{2N+1}{3}-frac{N+1}{2}right)=frac{N+1}{2}cdotfrac{4N+2-3N-3}{6}=frac{N+1}{2}cdotfrac{N-1}{6}=frac{N^2-1}{12} end{gather*} В частности, для игрального кубика: $$ N=6; p_i=frac16; M(X)=frac{6+1}{2}=3,5; D(X)=frac{6^2-1}{12}=2frac{11}{12} $$
Ответ: (M(X)=frac{N+1}{2}; D(X)=frac{N^2-1}{12})
Пример 2. Выведите формулы для мат.ожидания и дисперсии распределения Бернулли.
Случайная величина k имеет распределение Бернулли, если k принимает значения 1 или 0 с вероятностями p и 1-p соответственно. $$ P(0)=1-p=1, P(1)=p, kinleft{0;1right} $$
Закон распределения:
| (k_i) | 0 | 1 |
| (p_i) | 1-p | p |
Найдем математическое ожидание: $$ M(X)=0cdot (1-p)+1cdot p=p $$ Найдем дисперсию: begin{gather*} D(X)=(0^2cdot(1-p)+1^2cdot p)-M^2(X)=p-p^2=p(1-p)=pq end{gather*}
Типичным примером является бросание монеты, где (M(X)=p=0,5) и (D(X)=0,5cdot 0,5=0,25). Дисперсия максимальна для нефальшивой монеты.
Рассмотрим другой пример – бросание фальшивой монеты, для которой вероятность выпадения орла (k=1) равна p=0,7. Тогда (M(k)=p=0,7), дисперсия (D(k)=0,7cdot 0,3=0,21). Как и ожидалось, для фальшивой монеты средняя величина возрастает (70% бросков заканчивается выпадением орла). При этом дисперсия уменьшается.
Ответ: (M(X)=p, D(X)=pq)
Пример 3. Выведите формулы для мат.ожидания и дисперсии биномиального распределения.
Схема Бернулли – это последовательность независимых испытаний, в каждом из которых возможны только два исхода – «успех» и «неудача».
При этом вероятность успеха в каждом испытании постоянна и равна (pin(0;1)).
Вероятность неудачи в каждом испытании (q=1-p).
Вероятность того, что событие A появится в n испытаниях Бернулли ровно k раз, выражается биномиальным распределением: $$ P_n(k)=C_n^k p^k q^{n-k} $$
Математическое ожидание и дисперсию для одного опыта Бернулли мы получили в примере 2: (M(X)=p, D(X)=pq).
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. (X=X_1+X_2+…+X_n). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий (см. §41 справочника для 9 класса): begin{gather*} M(X)=M(X_1+X_2+…+X_n)=M(X_1)+M(X_2)+…+M(X_n)=\ =underbrace{p+p+…+p}_{n раз}=np end{gather*} По свойству дисперсии суммы независимых событий (см. §41 справочника для 9 класса): begin{gather*} D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)=\ =underbrace{pq+pq+…+pq}_{n раз}=npq end{gather*} Например, пусть событие A=«уронить молоток на ногу» имеет вероятность p=0,1.
Тогда для n=100 забиваний гвоздей вы в среднем уроните молоток на ногу
(M(X)=np=100cdot 0,1=10) раз
Дисперсия этого события (D(X)=npq=100cdot 0,1cdot 0,9=9)
СКО (sigma(X)=sqrt{D(X)}=3)
По правилу «трех сигм» интервал оценки: begin{gather*} 10-3cdot 3lt Xlt 10+3cdot 3\ -17lt Xlt 37\ 0leq Xleq 36 end{gather*} Скорее всего (вероятность 99,72%), вы уроните молоток от 0 до 36 раз.
Ответ: (M(X)=np, D(X)=npq)
Пример 4. Выведите формулы для мат.ожидания и дисперсии распределения Пуассона.
Если проводится очень много испытаний Бернулли, для каждого из которых вероятность появления события A мала: (nrightarrowinfty, prightarrow 0, nprightarrowlambda), вероятность того, что событие A появится ровно k раз выражается распределением Пуассона: $$ p_k(lambda)=frac{lambda^k}{k!}e^{-lambda}, k=inleft{0,1,2,…right} $$
Распределение Пуассона получается из биномиального распределения предельным переходом (nrightarrowinfty, prightarrow 0, nprightarrowlambda).
Найдем математическое ожидание как предел мат. ожидания биномиального распределения: $$ M(X)=lim_{nprightarrowlambda}M_B(X)=lim_{nprightarrowlambda}(np)=lambda $$ Т.е. параметр (lambda) является средним числом удачных исходов.
Дисперсия, если учесть что (prightarrow 0), а значит (q=1-prightarrow 1) $$ D(X)=underset{qrightarrow 1}{lim_{nprightarrowlambda}} D_B(X)=underset{qrightarrow 1}{lim_{nprightarrowlambda}}(npq)=lambdacdot 1=lambda $$
Например, в городе размерами 10х10 км болеет гриппом 1000 человек.
С какой вероятностью в комнате размерами 10х10 м:
а) не окажется больных;
б) окажется 1 больной?
Площадь города в метрах (S=(10^4)^2=10^8) м2
Площадь комнаты в метрах (s_0=10^2) м2
Среднее количество больных в комнате: (lambda=Nfrac{s_0}{S}=10^3cdotfrac{10^2}{10^3}=10^{-3}=0,001)
а) вероятность того, что в комнате не окажется больных: $$ p_0=frac{0,001^0}{0!}e^{-0,001}=e^{-0,001}approx 1-0,001=0,999 $$ Здесь мы использовали формулу приближенных вычислений (e^xapprox 1+x, xrightarrow 0) (см. §52 данного справочника).
б) вероятность того, что в комнате окажется один больной: $$ p_1=frac{0,001^1}{1!}e^{-0,001}=0,000999approx 0,001 $$ Вероятность всех остальных случаев пренебрежимо мала.
Таким образом, при малых (lambda) вероятности (p_0approx 1-lambda, p_1approxlambda), т.е. фактически мы получаем распределение Бернулли.
Ответ: (M(X)=lambda , D(X)=lambda)
Зная,
что
![]() ,
,
имеем:![]() +
+![]() =1
=1
– (0,2+0,1+0,2)=0,5;
 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2. Дисперсию найдём по формуле:

Ответ:
1.
![]() ;
;![]() .
.
2.
![]()
Задача
7. Плотность
распределения непрерывной случайной
величины Х имеет вид:

Найти:
а)
параметр
![]() ;
;
б)
функцию распределения
![]() ;
;
в)
вероятность попадания случайной величины
Х в интервал (3,5;5);
г)
математическое ожидание M
(X)
и дисперсию D
(X);
д)
построить графики функций f(x)
и F(x).
Решение:
а)
Найдём параметр
![]() .
.
Из
условия, что
 и значения данной случайной величины
и значения данной случайной величины
заключены в промежутке![]() ,
,
то
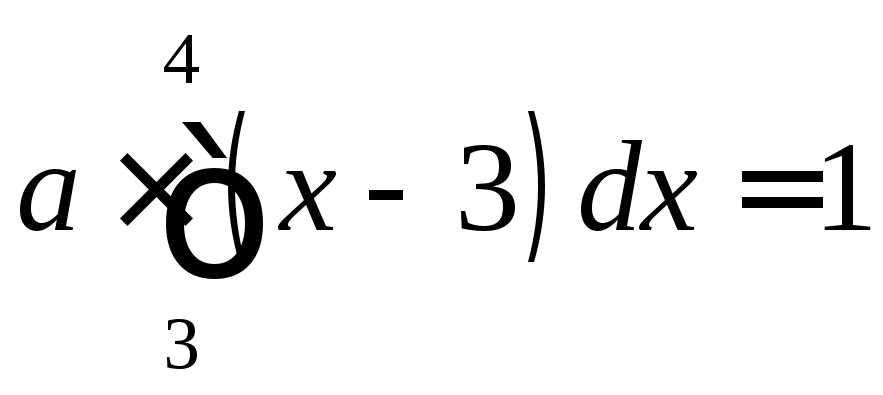 ,
,
откуда
 ;
;


б)
Найдём функцию распределения
![]() .
.
Из
свойства функции плотности
![]() имеем:
имеем:
![]() .
.
Рассмотрим три
интервала.

При
![]() .
.
 .
.
При
![]() .
.
 .
.
При
![]() .
.

Таким образом,

в)
Найдём вероятность
попадания случайной величины![]() в интервал
в интервал
(3,5; 5).

г) Найдём
математическое ожидание M
(X)
и дисперсию D
(X):


д)
построим графики функций f(x)
и F(x).
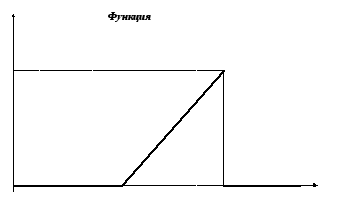
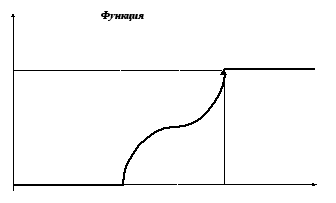
Ответ:
а)![]() .
.
б)

в)
![]()
г)![]()
Задача
8. Случайная
величина
![]() имеет биномиальное распределение. Найти
имеет биномиальное распределение. Найти
вероятность![]() ,
,
если математическое ожидание![]() ,
,
а дисперсия![]() .
.
Решение:
Для
биномиального закона распределения
имеем:
![]() ;
;![]() .
.
Зная
из условия, что математическое ожидание
![]() ,
,
а дисперсия
![]() .
.
Найдем
![]() из системы уравнений:
из системы уравнений:
Делим
одно уравнение на другое, получаем:
![]() ;
;
а
![]() ;
;
тогда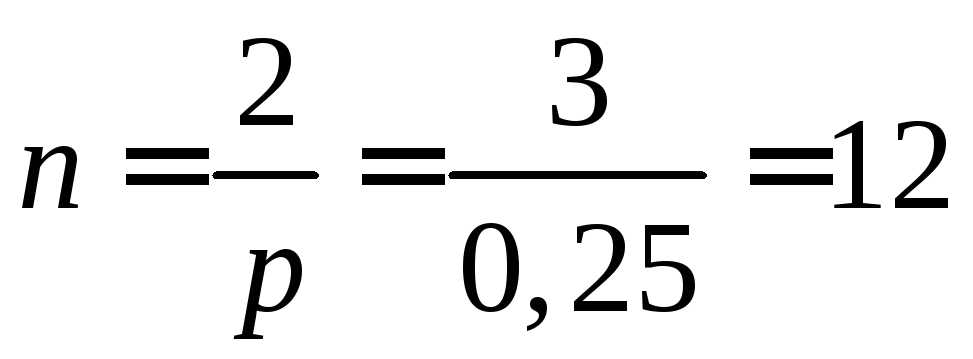 .
.
Вероятность:
![]() .
.
По
формуле Бернулли:
 .
.
Таким
образом, получим:

Окончательно
имеем:
![]()
Ответ:
![]()
Задача
9. Случайные
величины
![]() имеют равномерное, показательное и
имеют равномерное, показательное и
нормальное распределения соответственно.
Найти вероятности![]() ,
,
если у этих случайных величин математические
ожидания и средние квадратические
отклонения равны 2.
Решение:
1. Закон равномерного распределения имеет вид:

Найдём
параметры
![]() и
и![]() из условия:
из условия:
![]() ;
;
![]() .
.
Зная,
что математические ожидания и средние
квадратические отклонения равны 2,
найдем
![]() :
:
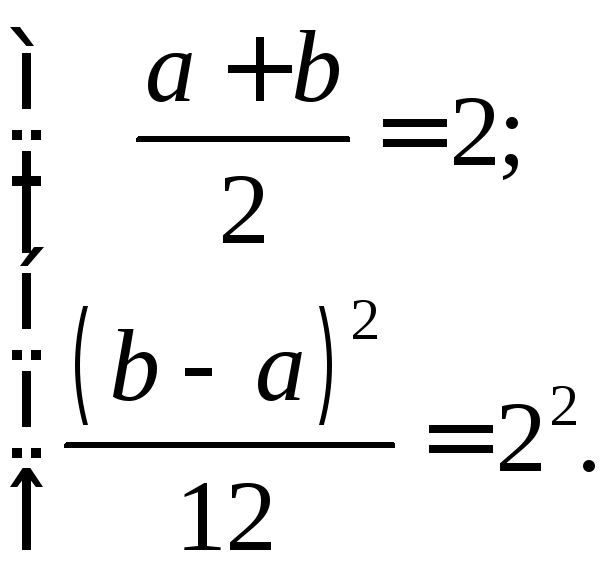
Решим
систему уравнений:
 ,
,
получим:

Так
как предполагается, что
![]() ,
,
то![]() .
.

Определяем
искомую вероятность:

2.
Показательное распределение имеет вид:

Для
показательного распределения:
![]() ;
;
![]() . Тогда
. Тогда![]() .
.

3.
Вероятность попадания в заданный
интервал нормального распределённой
случайной величины определяется как:
 .
.
Здесь
![]() .
.
Тогда

где
функция Лапласа
![]() определяется
определяется
по таблицам.
Ответ:
1.
![]()
2.
![]()
3.
![]()
Задача
10. Выборка
Х объемом
![]() измерений задана таблицей:
измерений задана таблицей:
-









5
13


19
10
3
![]() результаты
результаты
измерений;![]() частоты,
частоты,
с которыми встречаются значения![]() ;
;
![]() .
.
а)
Построить полигон относительных частот
 ;
;
б)
вычислить среднее выборочное
![]() ,
,
выборочную дисперсию![]() и среднее квадратическое отклонение
и среднее квадратическое отклонение![]() ;
;
в)
по критерию
![]() проверить гипотезу о нормальном
проверить гипотезу о нормальном
распределении генеральной совокупности
при уровне значимости![]() .
.
Решение:
а)
Построить
полигон относительных частот
 .
.
|
|
|
|
|
|
|
|
|
|
|
5 |
13 |
|
|
19 |
10 |
3 |
Вычисляя
относительные частоты:
 ,
,
получаем:
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
25 |
|
|
|
|
|
0,05 |
0,13 |
0,25 |
0,25 |
0,19 |
0,10 |
0,03 |
Построим
полигон относительных частот.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Дискретной называют двумерную величину, составляющие которой дискретны.
Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Закон
распределения дискретной двумерной случайной величины может быть задан:
а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;
б) аналитически, например в виде функции распределения.
Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность
, надо просуммировать
вероятности столбца
. Аналогично сложив
вероятности строки
получим вероятность
.
Пусть
составляющие
и
дискретны и имеют соответственно следующие
возможные значения:
;
.
Условным распределением составляющей
при
(j сохраняет одно и то же
значение при всех возможных значениях
) называют совокупность
условных вероятностей:
Аналогично
определяется условное распределение
.
Условные
вероятности составляющих
и
вычисляют соответственно по формулам:
Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ковариация (корреляционный момент)
Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки
.
Ковариацию
(корреляционный момент) можно найти по формуле:
Свойства ковариации
Свойство 1.
Ковариация двух независимых случайных величин равна нулю.
Свойство 2.
Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.
Свойство 3.
Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.
Коэффициент корреляции
Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.
Формула коэффициента корреляции:
Две
случайные величины
и
называют коррелированными, если их коэффициент
корреляции отличен от нуля.
и
называют некоррелированными величинами, если
их коэффициент корреляции равен нулю
Свойства коэффициента корреляции
Свойство 1.
Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.
Свойство 2.
Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.
Свойство 3.
Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Линейная регрессия
Рассмотрим
двумерную случайную величину
, где
и
– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины
в виде линейной функции величины
:
где
и
– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.
Линейная
средняя квадратическая регрессия
на
имеет вид:
Коэффициент
называют
коэффициентом регрессии
на
, а прямую
называют
прямой среднеквадратической регрессии
на
.
Аналогично
можно получить прямую среднеквадратической регрессии
на
:
Смежные темы решебника:
- Двумерная непрерывная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Задача 1
Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.
Требуется:
–
определить одномерные законы распределения случайных величин X и Y;
– найти
условные плотности распределения вероятностей величин;
–
вычислить математические ожидания mx и my;
–
вычислить дисперсии σx и σy;
–
вычислить ковариацию μxy;
–
вычислить коэффициент корреляции rxy.
| xy | 3 | 5 | 8 | 10 | 12 |
| -1 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 |
| 1 | 0.04 | 0.07 | 0.06 | 0.05 | 0.03 |
| 3 | 0.05 | 0.08 | 0.09 | 0.08 | 0.05 |
| 6 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Задана
дискретная двумерная случайная величина (X,Y).
а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.
| Y | X | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 30 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 |
| 40 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 |
| 50 | 0.05 | 0.03 | 0.02 | 0.02 | 0.01 |
| 70 | 0.1 | 0.03 | 0.04 | 0.03 | 0.01 |
| 90 | 0.1 | 0.04 | 0.01 | 0.07 | 0.2 |
Задача 3
Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.
|
x y |
1 | 2 | 3 |
| 1.5 | 0.03 | 0.02 | 0.02 |
| 2.9 | 0.06 | 0.13 | 0.03 |
| 4.1 | 0.4 | 0.07 | 0.02 |
| 5.6 | 0.15 | 0.06 | 0.01 |
Задача 4
Двумерная
случайная величина (X,Y) распределена по закону
| XY | 1 | 2 |
| -3 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| -3 | 0 | 0,2 |
Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.
Задача 5
Случайные
величины ξ и η имеют следующий совместный закон распределения:
P(ξ=1,η=1)=0.14
P(ξ=1,η=2)=0.18
P(ξ=1,η=3)=0.16
P(ξ=2,η=1)=0.11
P(ξ=2,η=2)=0.2
P(ξ=2,η=3)=0.21
1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.
2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).
3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}
4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.
Задача 6
Дан закон
распределения двумерной случайной величины (ξ,η):
| ξ=-1 | ξ=0 | ξ=2 | |
| η=1 | 0,1 | 0,1 | 0,1 |
| η=2 | 0,1 | 0,2 | 0,1 |
| η=3 | 0,1 | 0,1 | 0,1 |
1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания Mξ,
Mη и дисперсии Dξ, Dη
2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).
3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?
4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти Mγ и Dγ.
Задача 7
Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.
| XY | 1 | 2 | 4 |
| -2 | 0,25 | 0 | 0,25 |
| 1 | 0 | 0,25 | 0 |
| 3 | 0 | 0,25 | 0 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 8
Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.
| YX | -1 | 1 |
| -1 | 0,4 | 0,1 |
| 1 | 0,2 | 0,3 |
Задача 9
Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:
| X=-3 | X=0 | X=1 | |
| Y=-2 | 0,3 | ? | 0,1 |
| Y=1 | 0,1 | 0,1 | 0,2 |
Задача 10
Совместный
закон распределения пары
задан таблицей:
| xh | -1 | 0 | 1 |
| -1 | 1/12 | 1/4 | 1/6 |
| 1 | 1/4 | 1/12 | 1/6 |
Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.
Задача 11
Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции rxy?
| X | 20 | 25 | 30 | 35 |
| P | 0.1 | 0.1 | 0.4 | 0.4 |
и
Задача 12
Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):
| XY | 0 | 1 | 2 |
| -1 | ? | 0,1 | 0,2 |
| 1 | 0,1 | 0,2 | 0,3 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:
| ξη | -1 | 1 | 2 |
| 0 | 1/7 | 2/7 | 1/7 |
| 1 | 1/7 | 1/7 | 1/7 |
Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?
Задача 14
Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.
| XY | 2,3 | 2,9 | 3,1 | 3,4 |
| 0,2 | 0,15 | 0,15 | 0 | 0 |
| 2,8 | 0 | 0,25 | 0,05 | 0,01 |
| 3,3 | 0 | 0,09 | 0,2 | 0,1 |
Задача 15
Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.
| xy | 1 | 4 |
| -10 | 0,1 | 0,2 |
| 0 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 |
Задача 16
Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:
а) законы
распределения ее компонент и их числовые характеристики;
b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.
с)
ковариацию и коэффициент корреляции случайных величин X и Y;
d) составить матрицу ковариаций и матрицу корреляций;
e) вероятность попадания в область, ограниченную линиями y=16-x2 и y=0.
f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.
| XY | -1 | 0 | 1 | 2 |
| -1 | 0 | 1/6 | 0 | 1/12 |
| 0 | 1/18 | 1/9 | 1/12 | 1/9 |
| 2 | 1/6 | 0 | 1/9 | 1/9 |
Задача 17
Совместный
закон распределения случайных величин X и Y задан таблицей:
|
XY |
0 |
1 |
3 |
|
0 |
0,15 |
0,05 |
0,3 |
|
-1 |
0 |
0,15 |
0,1 |
|
-2 |
0,15 |
0 |
0,1 |
Найдите:
а) закон
распределения случайной величины X и закон распределения
случайной величины Y;
б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.
Задача 18
Известен
закон распределения двумерной случайной величины (X,Y).
а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);
б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;
в)
построить поле распределения и линию регрессии Y по X и X по Y;
г)
вычислить корреляционный момент (коэффициент ковариации) μxy и
коэффициент корреляции rxy.
|
|
5 | 20 | 35 |
| 100 | — | — | 0.05 |
| 115 | — | 0.2 | 0.15 |
| 130 | 0.15 | 0.35 | — |
| 145 | 0.1 | — | —- |
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
![]()
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
![]()
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
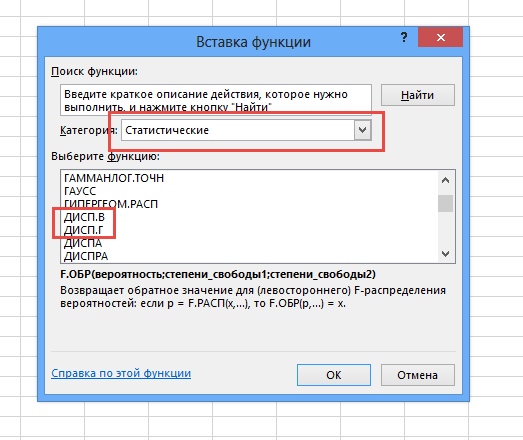
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
![]()
На практике формула стандартного отклонения следующая:
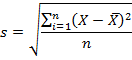
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
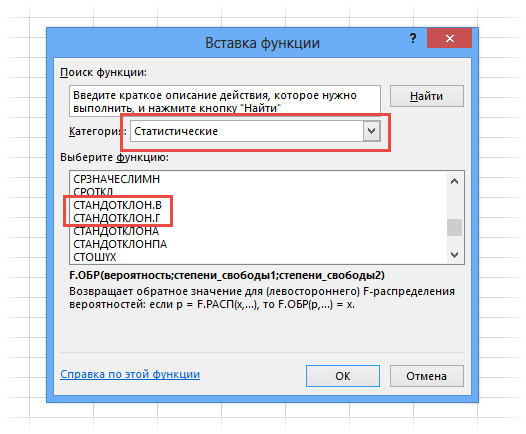
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
![]()
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
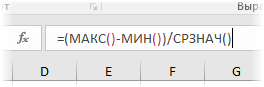
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
