Интервальное статистическое распределение
Если признак может
принимать любые значения из некоторого
промежутка, т.е. является непрерывной
случайной величиной, то необходимо
промежуток между наименьшим и наибольшим
значениями признака в выборке разбить
на несколько интервалов одинаковой
(или разной) длины. При
этом количество интервалов k
не должно
быть меньше 6 – 10 и больше 20 – 25 (выбор
числа интервалов зависит от объема
выборки n).
При подборе
количества интервалов можно пользоваться
приближенной формулой, которую предложил
американский статистик Sturgess
(Стерджесс):
![]()
– целая часть
числа х.
Затем определяем
длину частичного интервала группировки:
![]() ,
,
где R
=
![]() –
–
размах выборки.
Находим границы
каждого из непересекающихся частичных
интервалов
![]() :
:
a1
= xmin
–
![]() ;
;
b1
= a1
+ h;
a2
= b1;
b2
= a2
+ h
и т.д.
Далее
каждому интервалу требуется поставить
в соответствие число выборочных значений
признака, попавших в этот интервал. В
результате получим интервальное
статистическое распределение:
Таблица
3.3
|
Интервалы |
[a1; |
[a2; |
[a3; |
… |
[ak; |
|
Частоты |
m1 |
m2 |
m3 |
… |
mk |
Используя
интервальное статистическое распределение,
можно вычислить относительную частоту,
накопленную частоту, эмпирическую
функцию распределения, так же как и для
дискретного статистического распределения.
Если
в интервальном распределении каждый
интервал
![]()
заменить числом, лежащим в его середине
(ai
+
bi)/2,
то получим дискретное статистическое
распределение. Такая замена вполне
естественна, так как, например, при
измерении размера детали с точностью
до одного миллиметра, всем размерам из
промежутка [49,5 мм; 50,5 мм) будет
соответствовать одно число, равное 50.
Для графического
изображения интервального распределения
используется гистограмма.
Для ее построения в прямоугольной
системе координат по оси абсцисс
откладываем границы интервалов
группировки и на этих интервалах как
на основаниях строим прямоугольники,
высоты которых откладываются на оси
ординат. Различают:
а) гистограмму
абсолютных частот,
когда высота прямоугольника равна
![]() ;
;
б) гистограмму
относительных частот,
когда высота прямоугольника равна
![]() .
.
Гистограмма
является выборочным
аналогом графика плотности вероятности.
Площадь на интервале (aj;
am)
можно интерпретировать как приближенное
значение вероятности попадания случайной
величины Х
в этот интервал, т.е.
![]()
![]() .
.
Основное свойство
гистограммы:
ее площадь для абсолютных частот равна
n,
а для относительных частот равна
единице.
Отношение
относительной частоты к длине частичного
интервала h
называют плотностью
распределения частоты
на интервале
![]()
(рис. 3.5).

Рис. 3.5. Гистограмма
относительных частот
При построении
графика эмпирической функции распределения
для интервального ряда необходимо
учитывать, что функция определена только
на концах интервалов.
Таким образом,
статистическое распределение выборки
можно рассматривать как статистический
аналог для распределения генеральной
совокупности. Из-за случайных колебаний
эти два распределения, как правило, не
будут совпадать, но можно ожидать, что
при большом объеме выборки ее распределение
будет служить приближением для генеральной
совокупности, т.е.
![]()
![]() ,
,
если
![]() .
.
Пример
2.
Получены данные о выработке продукции
30-ю рабочими в отчетном месяце в процентах
к предыдущему месяцу
|
n |
Х |
|||||||||
|
1-10 |
125 |
91 |
82 |
93 |
101 |
111 |
109 |
103 |
121 |
90 |
|
11-20 |
79 |
105 |
115 |
95 |
84 |
130 |
104 |
117 |
127 |
107 |
|
21-30 |
85 |
76 |
98 |
104 |
126 |
113 |
98 |
84 |
113 |
123 |
Необходимо:
-
составить
интервальное статистическое распределение; -
построить
гистограмму относительных частот.
Решение
1. Определим величину
частичных интервалов:
![]()
Построим 6
непересекающихся интервалов:
[70,5; 81,5), [81,5; 92,5),
[92,5; 103,5),
[103,5; 114,5), [114,5;
125,5), [125,5; 136,5).
Первый интервал
[70,5; 81,5) содержит два значения (76 и 79),
поэтому m1
= 2. Второй
интервал [81,5; 92,5) содержит шесть значений
(82, 84, 84, 85, 90, 91), поэтому m2
= 6 и т.д.
Полученные данные внесем в таблицу
интервального статистического
распределения:
Таблица 3.4
|
Интервалы |
[70,5- 81,5) |
[81,5- 92,5) |
[92,5- 103,5) |
[103,5- 114,5) |
[114,5- 125,5) |
[125,5- 136,5) |
|
Частоты |
2 |
6 |
6 |
8 |
5 |
3 |
2. Для построения
гистограммы вычислим значения
относительных частот wi
и значения плотности распределения
частоты на интервале
![]() :
:
Таблица 3.5
|
Интервалы |
[70,5- 81,5) |
[81,5- 92,5) |
[92,5- 103,5) |
[103,5- 114,5) |
[114,5- 125,5) |
[125,5- 136,5) |
|
mi |
2 |
6 |
6 |
8 |
5 |
3 |
|
wi |
0,07 |
0,20 |
0,20 |
0,27 |
0,17 |
0,10 |
|
|
0,006 |
0,018 |
0,018 |
0,024 |
0,015 |
0,009 |
Изобразим
данные последней строки табл. 3.5 на
графике
(рис. 3.6).
Обведем гистограмму
плавной линией f*(x)
так, чтобы приблизительно были равны
площади, ограниченные гистограммой и
кривой f*(x),
которую называют эмпирической
плотностью распределения относительных
частот. В
генеральной совокупности ей соответствует
плотность вероятности f(x).
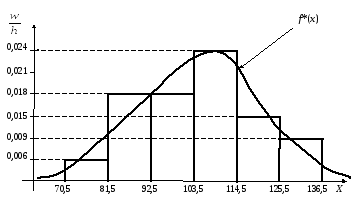 Рис.
Рис.
3.6. Гистограмма относительных частот
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.2. Интервальный вариационный ряд
Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина ![]() принимает слишком много различных значений
принимает слишком много различных значений ![]() . Зачастую ИВР появляется в результате
. Зачастую ИВР появляется в результате
изучения непрерывной характеристики объектов. Типично – это время, масса, размеры и другие физические величины.
Вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.
В таких ситуациях затруднительно либо невозможно применить тот же подход, что для дискретного ряда. Это связано с тем, что ВСЕ варианты ![]() различны (во многих случаях). И
различны (во многих случаях). И
даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, а фактически значения
всё равно отличаются хоть какими-то микрограммами.
Поэтому здесь используется другой подход, а именно определяется интервал,
в пределах которого варьируются значения ![]() , затем этот интервал делится на частичные интервалы (обычно равной длины
, затем этот интервал делится на частичные интервалы (обычно равной длины
![]() ) и по каждому частичному интервалу
) и по каждому частичному интервалу
подсчитываются частоты ![]() (либо
(либо ![]() ) – количество вариант, которые в него попали.
) – количество вариант, которые в него попали.
Если варианта попала на «стык» интервалов, то её относят к старшему интервалу.
Интервальный вариационный ряд (ИВР) статистической совокупности – это
упорядоченное множество смежных интервалов и соответствующие им частоты, в сумме равные
объёму совокупности. Дабы не плодить лишних букв и индексов, я никак не обозначил эти
интервалы. Придирчивый читатель, к слову, наверняка заметил, что через ![]() я обозначаю как исходные варианты, так и значения сгруппированного
я обозначаю как исходные варианты, так и значения сгруппированного
ряда.
Следует отметить, что исследуемая характеристика не обязана быть непрерывной, и мы как раз начнём с такой задачи:
Пример 6
По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в денежных
единицах):
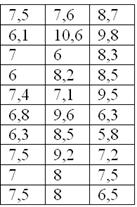
Составить вариационный ряд, построить гистограмму частот, гистограмму и полигон относительных частот + бонус:
эмпирическую функцию распределения.
Решение: очевидно, что перед нами выборочная совокупность
объема ![]() , и вопрос номер
, и вопрос номер
один: какой ряд составлять – дискретный или интервальный? Заметьте, что в
вопросе задачи ничего не сказано о характере ряда. Строго говоря, цены дискретны и среди них даже есть одинаковые. Однако они
могут быть округлены, да и разброс цен довольно велик. Поэтому здесь целесообразно провести интервальное разбиение.
Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только
ручка, карандаш, тетрадь и калькулятор.
Тактика действий похожа на работу с дискретным вариационным рядом. Сначала
окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все
значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае
напрашиваются промежутки единичной длины. Записываем их на черновик:
![]()
Теперь начинаем вычёркивать числа из исходного списка и записываем их в соответствующие колонки нашей импровизированной
таблицы:
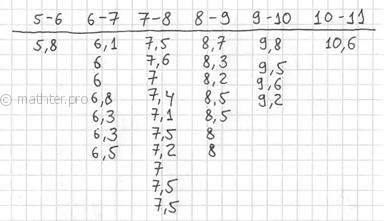
После этого находим самое маленькое число в левой колонке (минимальное значение) и самое большое число – в правой
(максимальное значение). Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
![]() ден. ед. – не забываем указывать
ден. ед. – не забываем указывать
размерность!
Вычислим размах вариации:
![]() ден. ед. – длина общего
ден. ед. – длина общего
интервала, в пределах которого варьируется цена.
Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт
существует формула Стерджеса:
![]() , где
, где ![]() – десятичный логарифм* от объёма выборки и
– десятичный логарифм* от объёма выборки и
![]() – оптимальное количество
– оптимальное количество
интервалов, при этом результат округляют до ближайшего левого целого значения.
* есть на любом более или менее приличном калькуляторе.
В нашем случае получаем: ![]() интервалов.
интервалов.
Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии
задачи прямо сказано, на какое количество интервалов следует проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует
придерживаться именно этого указания.
Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную
группировку:
![]() – длина частичного интервала. В
– длина частичного интервала. В
принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.
И коль скоро мы прибавили 0,04, то по пяти частичным интервалам получается «перебор»: ![]() . Посему от самой малой варианты
. Посему от самой малой варианты ![]() отмеряем влево 0,1 влево (половину «перебора») и к
отмеряем влево 0,1 влево (половину «перебора») и к
значению 5,7 начинаем прибавлять по ![]() ,
,
получая тем самым частичные интервалы. При этом сразу рассчитываем их середины ![]() (например,
(например, ![]() ) – они требуются почти во всех тематических задачах:
) – они требуются почти во всех тематических задачах:
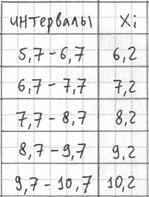
– убеждаемся в том, что самая большая варианта ![]() вписалась в последний частичный интервал и отстоит от его правого конца на
вписалась в последний частичный интервал и отстоит от его правого конца на
0,1.
Далее подсчитываем частоты по каждому интервалу. Для этого в черновой таблице обводим значения, попавшие в тот или
иной интервал, подсчитываем их количество и вычёркиваем:

Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11
штук) и вычеркнул и так далее. Варианта ![]() попала на «стык» интервалов и, согласно озвученному выше правилу, её следует
попала на «стык» интервалов и, согласно озвученному выше правилу, её следует
отнести к последующему интервалу ![]() .
.
В результате получаем интервальный вариационный ряд:
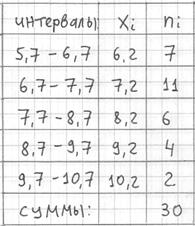
при этом обязательно убеждаемся в том, что ничего не потеряно:
![]() , ОК.
, ОК.
…Да, кстати, все ли представили свой любимый товар, чтобы было интереснее разбирать это длинное решение? J
Точно также как и в дискретном случае, интервальный вариационный ряд можно
(и нужно) изобразить графически. И здесь у нас весьма большое разнообразие. Но сначала добавим в таблицу дополнительные
столбцы и продолжим расчёты:
По каждому интервалу рассчитываем (не тушуемся): плотность частот ![]() , относительные частоты
, относительные частоты ![]() (округляем их до 2 знаков после запятой), а также плотность относительных
(округляем их до 2 знаков после запятой), а также плотность относительных
частот ![]() . Поскольку длина частичного
. Поскольку длина частичного
интервала ![]() , то вычисления заметно
, то вычисления заметно
упрощаются:
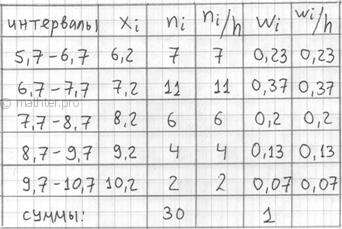
Если интервалы имеют разные длины ![]() , то
, то
при нахождении плотностей каждую частоту нужно разделить на длину своего интервала: ![]() . Но у нас группировка равноинтервальная, да не
. Но у нас группировка равноинтервальная, да не
абы какая, а с единичным частичным интервалом. Дело за чертежами. Один за другим:
 2.2.1. Гистограммы
2.2.1. Гистограммы
 2.1.2. Эмпирическая функция распределения
2.1.2. Эмпирическая функция распределения
| Оглавление |
Варианты для выполнения работы
I. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.
Почти все встречающиеся в жизни величины (урожайность сельскохозяйственных растений, продуктивности скота, производительность труда и заработная плата рабочих, объем производства продукции и т.д.) принимают неодинаковые значения у различных членов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствующих наблюдений, обследований.
В результате наблюдений получают сведения о численной величине изучаемого признака у каждого члена данной совокупности.
Пример. Имеются данные о размере прибыли 100 коммерческих банков. Прибыль, млн. рублей.
| 30,2 | 51,9 | 43,1 | 58,9 | 34,1 | 55,2 | 47,9 | 43,7 | 53,2 | 34,9 |
| 47,8 | 65,7 | 37,8 | 68,6 | 48,4 | 67,5 | 27,3 | 66,1 | 52,0 | 55,6 |
| 54,1 | 26,9 | 53,6 | 42,5 | 59,3 | 44,8 | 52,8 | 42,3 | 55,9 | 48,1 |
| 44,5 | 69,8 | 47,3 | 35,6 | 70,1 | 39,5 | 70,3 | 33,7 | 51,8 | 56,1 |
| 28,4 | 48,7 | 41,9 | 58,1 | 20,4 | 56,3 | 46,5 | 41,8 | 59,5 | 38,1 |
| 41,4 | 70,4 | 31,4 | 52,5 | 45,2 | 52,3 | 40,2 | 60,4 | 27,6 | 57,4 |
| 29,3 | 53,8 | 46,3 | 40,1 | 50,3 | 48,9 | 35,8 | 61,7 | 49,2 | 45,8 |
| 45,3 | 71,5 | 35,1 | 57,8 | 28,1 | 57,6 | 49,6 | 45,5 | 36,2 | 63,2 |
| 61,9 | 25,1 | 65,1 | 49,7 | 62,1 | 46,1 | 39,9 | 62,4 | 50,1 | 33,1 |
| 33,3 | 49,8 | 39,8 | 45,9 | 37,3 | 78,0 | 64,9 | 28,8 | 62,5 | 58,7 |
Из данной таблицы видно, что интересующий нас признак (прибыль банков) меняется от одного члена совокупности к другому, варьирует. Варьирование есть изменяемость признака у отдельных членов совокупности.
Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке и соответствующих им частот.
Число, показывающее, сколько раз повторяется в данной совокупности каждое значение признака, называется частотой.
Составим ранжированный вариационный ряд (выпишем варианты в порядке возрастания):
| 20,4 | 25,1 | 26,9 | 27,3 | 27,6 | 28,1 | 28,4 | 28,8 | 29,3 | 30,2 |
| 31,4 | 33,1 | 33,3 | 33,7 | 34,1 | 34,9 | 35,1 | 35,6 | 35,8 | 36,2 |
| 37,3 | 37,8 | 38,1 | 39,5 | 39,8 | 39,9 | 40,1 | 40,2 | 41,4 | 41,8 |
| 41,9 | 42,3 | 42,5 | 43,1 | 43,7 | 44,5 | 44,8 | 45,2 | 45,3 | 45,5 |
| 45,8 | 45,9 | 46,1 | 46,3 | 46,5 | 47,3 | 47,8 | 47,9 | 48,1 | 48,4 |
| 48,7 | 48,9 | 49,2 | 49,6 | 49,7 | 49,8 | 50,1 | 50,3 | 51,8 | 51,9 |
| 52,0 | 52,3 | 52,5 | 52,8 | 53,2 | 53,6 | 53,8 | 54,1 | 55,2 | 55,6 |
| 55,9 | 56,1 | 56,3 | 57,4 | 57,6 | 57,8 | 58,1 | 58,7 | 58,9 | 59,3 |
| 59,5 | 60,4 | 61,7 | 61,9 | 62,1 | 62,4 | 62,5 | 63,2 | 64,9 | 65,1 |
| 65,7 | 66,1 | 67,5 | 68,6 | 69,8 | 70,1 | 70,3 | 70,4 | 71,5 | 78,0 |
В нашем случае каждое значение признака (варианта вариационного ряда) повторилось только один раз, т.е. значение частоты для всех вариант равно единице. Перейдем к интервальному вариационному ряду, так как интересующий нас признак принимает дробные, практически не повторяющиеся значения.
Для этого необходимо определить число интервалов (классов) и длину интервала (классного промежутка), после чего произвести разноску, т.е. подсчитать для каждого интервала число вариант, попавших в него.
Количество классов устанавливают в зависимости от степени точности, с которой ведется обработка, и количества объектов в выборке. Считается удобным при объеме выборки (n) в пределах от 30 до 60 вариант распределять их на 6-7 классов, при n от 60 до 100 вариант — на 7-8 классов, при n от 100 и более вариант — на 9-17 классов.
Нужное количество групп также может быть ориентировочно вычислено по формуле Стерджесса:
![]()
где ![]() — число групп (классов, интервалов) ряда распределения; n — объем выборки.
— число групп (классов, интервалов) ряда распределения; n — объем выборки.
Можно также использовать выражение:
![]()
При ![]() они дают примерно одинаковые результаты.
они дают примерно одинаковые результаты.
В рассматриваемом примере о размере прибыли коммерческих банков, n=100. Применяя формулу Стерджесса, получим:
![]()
Однако ![]() Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.
Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.
Нахождение нужного количества групп и их размеров часто бывает взаимообусловлено. Для того, чтобы как-то определиться с числом интервалов, найдем размах вариации — разность между наибольшей и наименьшей вариантой:
![]()
где ![]() — размах вариации,
— размах вариации,
![]() — наибольшее значение варьирующего признака,
— наибольшее значение варьирующего признака,
![]() — наименьшее значение варьирующего признака.
— наименьшее значение варьирующего признака.
Найдем размах вариации для рассматриваемой задачи:
![]()
Для того, чтобы найти длину интервала (величину классового промежутка) необходимо разделить размах вариации на число классов и полученную величину округлить таким образом, чтобы было удобно производить сначала разноску, а затем и различные вычисления. Рекомендую округлять до единиц, до которых округлены варианты в исходной таблице, в нашем случае до десятых.
![]()
Согласно формуле получаем
![]()
Теперь необходимо определиться с началом первого интервала. Для этого можно использовать формулу:
![]()
![]()
Замечание. За начало первого интервала можно принять некоторое значение, несколько меньшее ![]() или само значение
или само значение ![]() . Далее в табличном виде я покажу оба варианта.
. Далее в табличном виде я покажу оба варианта.
Прибавив к началу первого интервала (нижней границе) шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, будем находить границы последующих интервалов до тех пор, пока не будет получено или перекрыто ![]() .
.
Таким образом, верхняя граница одного интервала одновременно является нижней границей другого интервала. Чтобы не возникало сомнений, в какой интервал отнести варианту, попавшую на границу, условимся относить ее к верхнему интервалу.
Составим теперь рабочую таблицу для построения интервального вариационного ряда и произведем подсчет частот вариант, попавших в тот или иной интервал.
Как и обещал покажу две таблицы построения ряда:
1. Отсчет ведем от ![]() , т.е. нижняя граница первого интервала совпадает с
, т.е. нижняя граница первого интервала совпадает с ![]() .
.
|
Группы банков по размеру прибыли (границы интервалов) |
Количество банков, принадлежащих данной группе (частоты, |
Накопленные частоты,
|
| 20,4 — 27,6 | 4 | 4 |
| 27,6 — 34,8 | 11 | 15 |
| 34,8 — 42 | 16 | 31 |
| 42 — 49,2 | 21 | 52 |
| 49,2 — 56,4 | 21 | 73 |
| 56,4 — 63,6 | 15 | 88 |
| 63,6 — 70,8 | 10 | 98 |
| 70,8 — 78 | 2 | 100 |
2. Начало первого интервала определяем с помощью формулы: ![]() .
.
|
Группы банков по размеру прибыли (границы интервалов) |
Количество банков, принадлежащих данной группе (частоты, |
Накопленные частоты,
|
| 16,8 — 24 | 1 | 1 |
| 24 — 31,2 | 9 | 10 |
| 31,2 — 38,4 | 13 | 23 |
| 38,4 — 45,6 | 17 | 40 |
| 45,6 — 52,8 | 23 | 63 |
| 52,8 — 60 | 18 | 81 |
| 60 — 67,2 | 11 | 92 |
| 67,2 — 74,4 | 7 | 99 |
| 74,4 — 81,6 | 1 | 100 |
Как мы видим в 1-м случае у нас получилось восемь интервалов, что полностью совпадает с результатом, который нам дала формула Стерджесса. Во втором случае у нас получилось девять интервалов, так как при поиске начала первого интервала пользовались специальной формулой.
Для дальнейшего исследования я буду пользоваться результатами второй таблицы, так как там ярко выражен модальный интервал (одна мода) и медиана практически точно попадает на середину вариационного ряда.
Мы получили интервальный вариационный ряд — упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.
II. Графическая интерпретация вариационных рядов.
| № п/п |
Границы интервалов,
|
Середины интервалов,
|
Частоты интервалов,
|
Относительные частоты
|
Плотность относит. частоты
|
Плотность частоты
|
| 1 | 16,8 — 24 | 20,4 | 1 | 0,01 | 0,001 | 0,139 |
| 2 | 24 — 31,2 | 27,6 | 9 | 0,09 | 0,013 | 1,250 |
| 3 | 31,2 — 38,4 | 34,8 | 13 | 0,13 | 0,018 | 1,806 |
| 4 | 38,4 — 45,6 | 42 | 17 | 0,17 | 0,024 | 2,361 |
| 5 | 45,6 — 52,8 | 49,2 | 23 | 0,23 | 0,032 | 3,194 |
| 6 | 52,8 — 60 | 56,4 | 18 | 0,18 | 0,025 | 2,500 |
| 7 | 60 — 67,2 | 63,6 | 11 | 0,11 | 0,015 | 1,528 |
| 8 | 67,2 — 74,4 | 70,8 | 7 | 0,07 | 0,010 | 0,972 |
| 9 | 74,4 — 81,6 | 78 | 1 | 0,01 | 0,001 | 0,139 |
Строим графики:





Далее найдем моду вариационного ряда:
![]()
где
![]() — начало модального интервала;
— начало модального интервала;
![]() — длина частичного интервала (шаг);
— длина частичного интервала (шаг);
 — частота предмодального интервала;
— частота предмодального интервала;
 — частота модального интервала;
— частота модального интервала;
![]() — частота послемодального интервала.
— частота послемодального интервала.
Определим модальный интервал — интервал, имеющий наибольшую частоту. Из таблицы видно, что модальным является интервал (45,6 — 52,8).
![]()
![]()
Медиана
Для интервального ряда медиана находится по формуле:
![]()
где
![]() — начало медианного интервала;
— начало медианного интервала;
![]() — длина частичного интервала (шаг);
— длина частичного интервала (шаг);
![]() — объем совокупности;
— объем совокупности;
![]() — накопленная частота интервала, предшествующая медианному;
— накопленная частота интервала, предшествующая медианному;
![]() — частота медианного интервала.
— частота медианного интервала.
Определим медианный интервал — интервал, в котором впервые накопленная частота превышает половину объема выборки.Так как объем выборки n=100, то n/2=50. По таблице найдем интервал, где впервые накопленные частоты превысят это значение. Таким является интервал (45,6 — 52,8).
Получаем,
![]()
III. Расчет сводных характеристик выборки.
Для определения ![]() составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).
составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).
Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. В нашем случае С=49,2.
Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.
Условными называют варианты, определяемые равенством:
![]()
Произведем расчет условных вариант согласно формуле:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| N п/п |
Середины интервалов,
|
Частоты интервалов,
|
Условные варианты,
|
Произведения частот и условных вариант,
|
Произведения частот и условных вариант,
|
Произведения частот и условных вариант,
|
Произведения частот и условных вариант,
|
Произведения частот и условных вариант,
|
Произведения частот и условных вариант,
|
| 1 | 20,4 | 1 | -4 | -4 | 16 | -64 | 256 | 9 | 81 |
| 2 | 27,6 | 9 | -3 | -27 | 81 | -243 | 729 | 36 | 144 |
| 3 | 34,8 | 13 | -2 | -26 | 52 | -104 | 208 | 13 | 13 |
| 4 | 42 | 17 | -1 | -17 | 17 | -17 | 17 | 0 | 0 |
| 5 | 49,2 | 23 | 0 | 0 | 0 | 0 | 0 | 23 | 23 |
| 6 | 56,4 | 18 | 1 | 18 | 18 | 18 | 18 | 72 | 288 |
| 7 | 63,6 | 11 | 2 | 22 | 44 | 88 | 176 | 99 | 891 |
| 8 | 70,8 | 7 | 3 | 21 | 63 | 189 | 567 | 112 | 1792 |
| 9 | 78 | 1 | 4 | 4 | 16 | 64 | 256 | 25 | 625 |
Контроль:
![]()
![]()
![]()
Контроль:
![]()
![]()
![]()
![]()
Равенство выполнено, следовательно вычисления произведены верно.
Вычислим условные моменты 1-го, 2-го, 3-го и 4-го порядков:
![]()
![]()
![]()
![]()
Найдем выборочные среднюю, дисперсию и среднее квадратическое отклонение :
![]()
![]()
![]()
Также для оценки отклонения эмпирического распределения от нормального используют такие характеристики, как асимметрия и эксцесс.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
![]()
Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева — отрицательна.
Эксцесс эмпирического распределения определяется равенством:
![]()
где ![]() — центральный эмпирический момент четвертого порядка.
— центральный эмпирический момент четвертого порядка.
Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.
Вычисляем центральные эмпирические моменты третьего и четвертого порядков:
![]()
![]()
Найдем асимметрию и эксцесс:
![]()
![]()
IV. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.
Проверим генеральную совокупность значений размера прибыли банков по критерию Пирсона ![]()
Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу ![]() : генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:
: генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:
![Rendered by QuickLaTeX.com [chi^2_{nabl}=sum frac{ {(n_i-n_i^{'})}^2}{n_i^{'}}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-43685ed67e69272b6c950828a97acd89_l3.png)
и по таблице критических точек распределения ![]() , по заданному уровню значимости
, по заданному уровню значимости ![]() и числу степеней свободы
и числу степеней свободы ![]() найти критическую точку
найти критическую точку ![]() , где s — количество интервалов.
, где s — количество интервалов.
Если ![]() — нет оснований отвергнуть нулевую гипотезу.
— нет оснований отвергнуть нулевую гипотезу.
Если ![]() — нулевую гипотезу отвергают.
— нулевую гипотезу отвергают.
Найдем теоретические частоты ![]() , для этого составим следующую таблицу.
, для этого составим следующую таблицу.
|
Середины интервалов,
|
Частоты интервалов,
|
Произведем расчет,
|
Произведем расчет,
|
Значения функции Гаусса,
|
Произведем расчет,
|
Теоретические частоты,
|
| 20,4 | 1 | -28,152 | -2,23 | 0,0332 | 57 | 2 |
| 27,6 | 9 | -20,952 | -1,66 | 0,1006 | 57 | 6 |
| 34,8 | 13 | -13,752 | -1,09 | 0,2203 | 57 | 13 |
| 42 | 17 | -6,552 | -0,52 | 0,3485 | 57 | 20 |
| 49,2 | 23 | 0,648 | 0,05 | 0,3984 | 57 | 23 |
| 56,4 | 18 | 7,848 | 0,62 | 0,3292 | 57 | 19 |
| 63,6 | 11 | 15,048 | 1,19 | 0,1965 | 57 | 11 |
| 70,8 | 7 | 22,248 | 1,77 | 0,0833 | 57 | 5 |
| 78 | 1 | 29,448 | 2,34 | 0,0258 | 57 | 1 |
Вычислим ![]() , для чего составим расчетную таблицу.
, для чего составим расчетную таблицу.
| 1 | 1 | 2 | -1 | 1 | 0,5 | 1 | 0,5 |
| 2 | 9 | 6 | 3 | 9 | 1,5 | 81 | 13,5 |
| 3 | 13 | 13 | 0 | 0 | 0 | 169 | 13 |
| 4 | 17 | 20 | -3 | 9 | 0,45 | 289 | 14,45 |
| 5 | 23 | 23 | 0 | 0 | 0 | 529 | 23 |
| 6 | 18 | 19 | -1 | 1 | 0,05 | 324 | 17,05 |
| 7 | 11 | 11 | 0 | 0 | 0 | 121 | 11 |
| 8 | 7 | 5 | 2 | 4 | 0,8 | 49 | 9,8 |
| 9 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 100 | 100 |
Наблюдаемое значение критерия,
|
103,30 |
Контроль:
![Rendered by QuickLaTeX.com [sumfrac{n_i^2}{n_i^{'}}-n=sum frac{{(n_i-n_i^{'})}^2}{n_i^'}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6c32fcc2a5c6b3b4b603ae3d99533b4a_l3.png)
![]()
![]()
Вычисления произведены правильно.
Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s=9;
![]()
По таблице критических точек распределения ![]() по уровню значимости
по уровню значимости ![]() и числу степеней свободы k=6 находим
и числу степеней свободы k=6 находим ![]()
Так как ![]() — нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
— нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
На рисунке построены нормальная (теоретическая) кривая по теоретическим частотам (зеленый график) и полигон наблюдаемых частот (коричневый график). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

V. Интервальные оценки.
Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью ![]() покрывает заданный параметр.
покрывает заданный параметр.
Интервальной оценкой (с надежностью ![]() ) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней
) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней ![]() при известном среднем квадратическом отклонении
при известном среднем квадратическом отклонении  генеральной совокупности служит доверительный интервал
генеральной совокупности служит доверительный интервал
![]()
где ![]() — точность оценки, n — объем выборки, t — значение аргумента функции Лапласа
— точность оценки, n — объем выборки, t — значение аргумента функции Лапласа ![]() (см. приложение 2), при котором
(см. приложение 2), при котором ![]() ;
;
при неизвестном среднем квадратическом отклонении  (и объеме выборки n<30)
(и объеме выборки n<30)
![]()
![]()
где S — исправленное выборочное среднее квадратическое отклонение, ![]() находят по таблице приложения по заданным n и
находят по таблице приложения по заданным n и ![]() .
.
В нашем примере среднее квадратическое отклонение известно, ![]() . А также
. А также ![]() ,
, ![]() ,
, ![]() . Поэтому для поиска доверительного интервала используем первую формулу:
. Поэтому для поиска доверительного интервала используем первую формулу:
![]()
Все величины, кроме t, известны. Найдем t из соотношения ![]() По таблице приложения находим t=1,96. Подставив t=1,96,
По таблице приложения находим t=1,96. Подставив t=1,96, ![]() ,
, ![]() ,
, ![]() в формулу, окончательно получим искомый доверительный интервал:
в формулу, окончательно получим искомый доверительный интервал:
![]()
![]()
![]()
Интервальной оценкой (с надежностью ![]() ) среднего квадратического отклонения
) среднего квадратического отклонения  нормально распределенного количественного признака Х по «исправленному» выборочному среднему квадратическому отклонению S служит доверительный интервал
нормально распределенного количественного признака Х по «исправленному» выборочному среднему квадратическому отклонению S служит доверительный интервал
![]() (при q<1), (*)
(при q<1), (*)
![]() (при q>1),
(при q>1),
где q — находят по таблице приложения по заданным n и ![]() .
.
По данным ![]() и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив
и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив ![]() в соотношение (*), получим доверительный интервал:
в соотношение (*), получим доверительный интервал:
![]()
![]()
Длина – частичный интервал
Cтраница 1
Длины частичных интервалов должны быть настолько малыми, чтобы внутри каждого из них плотность вероятностей f ( t) не слишком сильно менялась; с другой стороны, количество наблюдении в каждом частичном интервале не должно быть слишком малым. Затем проводят плавную кривую у f ( x) таким образом, чтобы площадь, расположенная между крииой и осью абсцисс, как можно меньше отличалась от суммы площадей прямоугольников.
[1]
Если число точек деления неограниченно возрастает, а длина наибольшего частичного интервала стремится к нулю для всего интервала [ а, Ь ], то то же самое, очевидно, будет выполняться и для интервалов [ а, с ] и [ с, Ь ]; при этом первая сумма стремится к интегралу в пределах от а до с, а вторая – к интегралу в пределах от с до Ь, и мы получаем требуемое равенство.
[2]
Если число точек деления неограниченно возрастает, а длина наибольшего частичного интервала стремится к нулю для всего интервала [ а, Ь, то то же самое, очевидно, будет выполняться и для интервалов [ а, с ] и [ с, Ь, при этом первая сумма стремится к интегралу в пределах от а но с, а вторая – к интегралу в пределах от с до Ь, и мы получаем требуемое равенство.
[3]
Это значит, что при построении интегральной суммы разность х – xi 1 уже не является длиной частичного интервала, а отличается от нее знаком.
[4]
Определенным интегралом называется предел, к которому стремится и-я интегральная сумма ( А) при стремлении к нулю длины наибольшего частичного интервала.
[5]
Определенным интегралом называется предел, к которому стремится – я интегральная сумма ( А) при стремлении к нулю длины наибольшего частичного интервала.
[6]
Сформулированная выше замечательная теорема показывает, что для непрерывных функций разница между этими суммами стирается по мере возрастания числа точек деления и убывания длины наибольшего частичного интервала, совсем исчезая в пределе.
[7]
При вычислении выборочной дисперсии для уменьшения ошибки, вызванной группировкой ( особенно при малом числе интервалов), делают поправку Шепиарда, а именно вычитают из вычисленной дисперсии 1 / 12 квадрата длины частичного интервала.
[8]
При вычислении выборочной дисперсии для уменьшения ошибки, вызванной группировкой ( особенно при малом числе интервалов), делают поправку Шеппарда, а именно вычитают из вычисленной дисперсии 1 / 12 квадрата длины частичного интервала.
[9]
Точно эти интервалы определяются в цикле по А. В строке 1020 вычисляется текущее значение верхней границы частичного интервала. После того как найдена длина частичного интервала Н, оператором GOSUB 5000 вызывается подпрограмма для решения системы дифференциальных уравнений.
[10]
Если этого не предусмотреть, то может так случиться, что ступенчатая фигура не будет неограниченно приближаться к криволинейной трапеции. Тогда ломаная может неограниченно приближаться к дуге А0Ап 1 заданной линии yf ( x), но вовсе не будет приближаться к дуге Ап гАп и постоянная часть трапеции х 1Ап 1АПЬ не будет при этом процессе покрываться нашими фигурами. Таким образом, по площадям этих фигур мы никак не сможем определить площадь трапеции. Если же указать, что длина наибольшего частичного интервала стремится к нулю, то из этого следует, что число л частичных интервалов неограниченно возрастает.
[11]
Если этого не предусмотреть, то может так случиться, что ступенчатая фигура не будет неограниченно приближаться к криволинейной трапеции. Тогда ломаная может неограниченно приближаться к дуге A0An i заданной линии yf ( x), но вовсе не будет приближаться к дуге Ап гАп и постоянная часть трапеции xn 1An 1Anb не будет при этом процессе покрываться нашими фигурами. Таким образом, по площадям этих фигур мы никак не сможем определить площадь трапеции. Если же указать, что длина наибольшего частичного интервала стремится к нулю, то из этого следует, что число л частичных интервалов неограниченно возрастает.
[12]
Страницы:
1
