Длина дуги арки как найти

Формула Пепина для расчёта длины дуги АРКИ

Формула Пепина для расчёта длины дуги АРКИ.

На днях исполнится мне 54 года. На очереди 54 статья по счётчику «Прозы». В свёртке число 54 даёт простое число 9 – точно такое же число получается при свёртке моего полного настоящего ФИО. Пришла идея «отметить» такое совпадение чисел интересной статьёй. Решил опубликовать мою формулу для расчета длины дуги арки. (Первую арку я изготовил, как ни странно, тоже 9 лет назад.)
Кому это нужно?
Это нужно таким же, как я людям, которые при изготовлении металлоизделий: арочных козырьков, беседок, теплиц и разного рода крыш – сталкиваются с необходимостью расчетов заготовок для гнутья дуг, скажем из профильной трубы разного размера.
Арки из металлопрофиля изготавливаются прокатыванием металла в трёхвалковых вальцах. За счёт многократного прокатывания «туда-обратно» прямая заготовка металла приобретает форму части дуги окружности. Дуга получается, конечно, неточной геометрической копией части окружности. Но вполне достаточным приближением к окружности. Точность зависит от нескольких факторов: от однородности трубы, от степени износа валов вальцов, от расстояния между валами вальцов и от количества проходов – количества раз прокатывания « туда-обратно». Ну, и конечно от искусства и навыков изготовителя.
Но моя идея состоит в том, что если знать длину заготовки металла для конкретной дуги, то при прокатывании заготовки нужно только замерять расстояние между концами заготовки. И когда при изготовлении дуги расстояние между концами заготовки совпадёт с размером основания дуги (прямой, ограничивающей сегмент дуги снизу), то дуга обретает заданные размеры, она готова.
Но как рассчитать длину дуги, когда обычно для козырька или беседки задаются величина основания сегмента дуги и высоте дуги? Хорошо, если уже есть готовый чертёж, который нарисован архитектором, дизайнером или рекламщиком. Там хотя бы есть радиус дуги. И тогда можно на подходящей поверхности начертить часть окружности с таким радиусом. При изготовлении первых дуг так приходилось делать: чертить дугу на земле или на полу. И замерять длину заготовки для дуги, прикладывая к нарисованной дуге рулетку. Потом отрезать заготовку такой длины и прокатывать до совпадения с размером основания сегмента дуги.
Глядя на то, как красиво вырисовываются дуги в графических редакторах на компьютере, мне всё время думалось, что должна быть такая формула, по которой можно высчитать длину дуги, зная только размеры основания и высоты дуги. Перекопав доступную литературу по математике и по строительству, я не смог найти такую формулу. НО думаю, что, наверное, она где-то есть. Поэтому решил попробовать самому вывести эту формулу. Благо дети учились в старших классах школы и были учебники по геометрии. И… Вот, с помощью учебника геометрии 10 или 11 класса, точно уже не помню, мне удалось вывести такую формулу. Само доказательство, даже уже приготовленное в виде статьи ещё году в 2005-ом, сгинуло вместе со всей информацией, когда «сдох» очередной жёсткий диск компьютера, но сам способ вычисления длины дуги сегмента остался в виде алгоритма записанного в рабочей тетради, благодаря тому, что я этим алгоритмом постоянно пользуюсь.
Вот этот метод вычисления длины дуги по основанию и высоте дуги и свою формулу я предлагаю всем заинтересованным людям.
Посмотрим на рисунок. Допустим нам нужно найти длину верхней дуги изображённой арки. Рисуем на этой арке прямоугольный треугольник. Одним катетом является высота арки – это катет b (катет противолежащий углу альфа). Он же является частью радиуса. Второй катет – a (катет прилежащий к углу альфа), является половиной основания сегмента арки.
Исходя из величин катетов этого треугольника, мы можем найти длину дуги арки (сегмента) по формуле (3) , которую я нескромно назвал формулой Пепина. (3)
Как видим, для получения величины длины дуги нам нужно знать угол альфа. Величину этого угла мы можем найти через отношение известных нам размеров катетов, то есть через тангенс угла альфа. Для этого мы согласно формуле (1) поделим величину катета b на величину катета a.
Сократив (округлив) полученное значения тангенса до тысячной мы по сокращённой таблице тангенсов Брадиса, приведённой на рисунке, находим значение угла альфа. В колонках tg ; приведена только дробная часть тангенса (для простоты отброшено 0 целых). Как показывает мой опыт, что для удовлетворительной точности изготовления дуги достаточно знать величину градуса с десятой частью угла. Но у нас таблица только с целыми значениями градусов. Если привести с десятыми, то величина таблицы увеличиться тоже в 10 раз. Мне показалось, что тогда долго искать придётся. Желающие, конечно, могут взять полную таблицу тангенсов Брадиса и пользоваться ей. Я поступаю, так нахожу десятую часть градуса с помощью прикидки «в уме». Между целыми градусами разница от 18 до 34 тысячных градуса. Разделив эту разницу на 10, я получаю значение тангенса для десятой доли угла альфа. И уже, прикинув, сколько не хватает или лишку до ближайшего целого градуса, я нахожу десятичное значение градуса угла альфа. Кто-то, может быть, построит себе таблицу с точностью до десятой доли градуса.

Далее нам нужно рассчитать величину радиуса дуги R. Для этого выведена формула (2)

Далее, значения угла альфа и радиуса подставляем в формулу Пепина (3) и получаем длину дуги. Потом, режем заготовку металла такой длины и прокатываем до тех пор, пока расстояние между концами заготовке не станет равным величине основания дуги.
Прежде чем рассмотреть конкретный пример, напомню, что если у вас дуга равна точно полуокружности, то вы можете воспользоваться классической формулой длины окружности которая равна Пи R (полуокружность).
Рассмотрим пример. Пусть у нас высота арки 87 сантиметров , а ширина (величина основания сегмента 256 сантиметров ( 2 метра 56 сантиметров)

Шаг 1. Формула (1)
Ищем тангенс угла альфа. Для этого поделим 87 сантиметров на половину основания, то есть на 128 сантиметров. Получаем 0,6796875. Округляя до тысячной – получаем 0, 680. Это значение попадает между 34 и 35 градусами. Между ними разница в 25 «единиц». Значит одной десятой градуса соответствует 2, 5 «единицы». Между значением 34 градуса = 0, 675 и полученными 0, 680 всего пять «единиц». 5 «единиц» поделим на 2, 5 и получаем, что к 34 градусам нужно добавить 2 десятых градуса. Значит, искомая величина угла альфа равна 34, 2 градуса.

Шаг 2. (Формула (2)
Вычисляем значение радиуса. Катет b = 0.87 метра, В квадрате это будет 0,7569. Катет a = 1.28 метра, следовательно, в квадрате это будет =1, 6384. Сумма квадратов катетов = 2,3953. Теперь это число поделим на удвоенный катет b , что соответствует 1.74 метра. Получаем в результате значения радиуса равное 1.3766.. метра. Нас устроит такое значение, и даже значение 1,38 метра.
Шаг 3 Формула (3)
Подставляем полученные значения в формулу Пепина.
Угол 34,2 градуса помножаем на радиус 1.38 метра и помножаем на коэффициент 0.07 (семь сотых) и получаем величину длины дуги = 3, 30372… Для практических целей берём заготовку длиной 3 метра 30 сантиметров.
Практически у каждых вальцов дуга не прокатывает самые концы дуги из-за того, что между валами вальцов есть расстояние. У меня на небольших вальцах это непрокатываемое расстояние всего по семь сантиметров с каждого конца. На качество изделия эти прямые части не влияют. Поэтому я беру заготовки по рассчитанной по формуле (3) величине. Тем, кто хочет иметь более полное соответствие дуги геометрии окружности, или у кого большие не прокатываемые концы, то для этого следует к рассчитанной длине дуги прибавить удвоенное расстояние не прокатываемого конца, и замерять величину основания с учетом (вычетом) этого удлинения заготовки.
Всем успехов в работе и построение арок, которые находят всё большее и большее применение в нашей жизни!
Жжуков Иван. 20 октября 2012 года. г. Орёл.

Дня через два опубликую эту статью на сайте Гайдпарк, там она будет иметь более удобный для чтения вид.

Что такое хорда окружности в геометрии, её определение и свойства

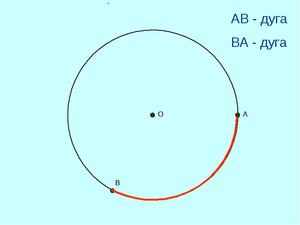Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.

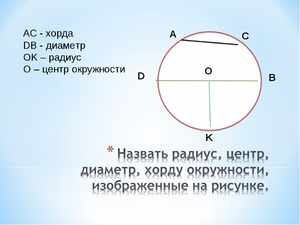
В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.

Как построить геометрическую хорду

Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.

Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.

Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.

Свойства

Существует ряд закономерностей, связывающих между собой хорды и центр круга:

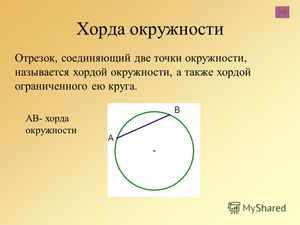1. Если расстояния от хорд до центра равны между собой, то такие хорды тоже равны между собой.
2. Существует также обратная зависимость — если длины отрезков равны между собой, то расстояния от них до центра тоже будут равными.
3. Чем большую длину имеет стягивающий отрезок прямой, тем меньше расстояние от него до центра окружности. И наоборот, чем она меньше, чем расстояние от указанного отрезка до центра описываемого круга больше.
4. Чем больше расстояние от «струны» до центра, тем меньше длина этой оси. Справедливой будет также и обратная взаимосвязь — чем меньше расстояние от центра до хорды, тем больше длина.
5. Хорда в геометрии, которая имеет максимально возможную для этой окружности длину, называется диаметром круга. Такая ось проходит через центр и делит её на две равные части.
6. Отрезок с наименьшей длиной представляет собой точку.
7. Если ось представляет собой точку, то расстояние от неё до центра круга будет равняться радиусу.

Взаимосвязь с радиусом и диаметром

Вышеуказанные математические понятия связаны между собой следующими закономерностями:

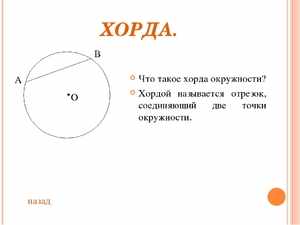1. Если описываемый отрезок не является диаметром этого круга, и этот диаметр делит его пополам, то эта ось и диаметр перпендикулярны между собой.
2. С другой стороны, диаметр, который перпендикулярен любой произвольной стягивающей, делит её на две равные части.
3. Если ось не является диаметром, и последний делит её на две равные части, то он делит пополам и обе дуги, которые стянуты этим отрезком.
4. Если диаметр делит на две одинаковые части дугу, то этот же диаметр делит пополам отрезок, который эту дугу стягивает.
5. Если диаметр строго перпендикулярен описываемой величине, то он делит на две половины каждую дугу, которую ограничивает эта линия.
6. Если диаметр круга делит пополам отрезок кривой, то он располагается перпендикулярно оси, которая этот отрезок стягивает.

Хорда и радиус

Между этими понятиями существуют следующие связи:

1. Если стягивающий отрезок не служит диаметром круга, и радиус разделяет её пополам, то такой радиус является перпендикулярным ей.
2. Существует также обратная зависимость — радиус, который перпендикулярен оси, делит её на две одинаковые составные части.
3. Если ось не выступает диаметром этого круга, и радиус делит её пополам, то этот же радиус делит пополам и дугу, которая стягивается.
4. Радиус, который делит пополам дугу, также делит и отрезок, который эту дугу стягивает.
5. Если радиус является перпендикулярным стягивающей линии, то он делит пополам часть кривой, которую она ограничивает.
6. Если радиус окружности разделяет на две идентичные части дугу, то он является перпендикулярным линии, которая эту дугу стягивает.

Отношения со вписанными углами

Углы, вписанные в окружность, подчиняются следующим правилам:

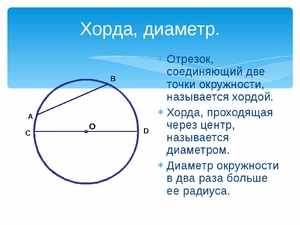1. Если углы, вписанные в окружность, опираются на одну и ту же линию, и их вершины расположены по одну сторону, то такие углы равны между собой.
2. Если два вписанных в круг угла опираются на одну и ту же линию, но их вершины расположены по разные стороны этой прямой, то сумма таких углов будет равняться 180 градусам.
3. Если два угла — центральный и вписанный — опираются на единую линию, и их вершины располагаются по одну сторону от неё, то величина вписанного угла будет равняться половине центрального.
4. Вписанный угол, который опирается на диаметр круга, является прямым.
5. Равные между собой по размеру отрезки стягивают равные центральные углы.
6. Чем больше величина стягивающего отрезка, тем больше величина центрального угла, который она стягивает. И наоборот, меньшая по размеру линия стягивает меньший центральный угол.
7. Чем больше центральный угол, тем больше величина отрезка прямой, который его стягивает.

Взаимодействия с дугой

Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:

1. Две равные между собой хорды стягивают равные дуги.
2. Если рассматривать две дуги, размер которых меньше половины окружности, то чем больше дуга, тем больше хорда, которая будет её стягивать. Напротив, меньшая дуга будет стягиваться меньшей по величине хордой.
3. Если же дуга превышает половину окружности, то здесь присутствует обратная закономерность: чем меньше дуга, тем больше хорда, которая её стягивает. И чем больше дуга, тем меньше ограничивающая её хорда.

Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.

АРОЧНЫЕ КОНСТРУКЦИИ

АРОЧНЫЕ КОНСТРУКЦИИ

Происхождение, история, физические свойства и виды арок.

Арка – одна из древнейших архитектурных форм, на заре цивилизации она не была просто перекрытием, она несла в себе ритуально-символический смысл. Слово «арка» происходит от латинского «arcus» – дуга, но существует версия, что слово происходит от ивритского «арука», что означает «длинная, тянущаяся». С развитием каменного зодчества, арки приобрели повсеместный характер и стали частью многих типов сооружений. Сегодня арка является популярным декоративным элементом, подчеркивающим изящность и одновременно монументальность объекта, наряду с этим они заняли нишу в промышленном строительстве и стали неотъемлемым элементом многих хозяйственных построек.

Так как же появился столь прекрасный и незаменимый элемент? Откуда человек смог его почерпнуть? Какие схожие конструкции присутствуют в архитектуре и природе? Как развивалась и трансформировалась арка в ходе истории, и какие приобретала значения для человечества? Люди часто забывают о значимости обыденных вещей и редко задумываются о происхождении, на первый взгляд привычного и естественного. Потому-то и стоит периодически освещать простые, знакомые каждому и давно забытые как проблема, вещи и явления.

Изучение арок, как основного элемента храмовой и соборной архитектуры, а так же, и как отдельно стоящего произведения монументальной архитектуры – триумфальной арки, занимает в истории искусств огромное место. Применение арок как пролетов или несущих конструкций имело повсеместный характер уже в начале нашей эры, а оформление арочной конструкцией входа и окон – с 10 по 15 века являлось каноническим и предопределяло становление архитектурных стилей. Возможность распределять нагрузку всего здания на одни лишь арки сыграла роль в становлении и развитии искусства постройки готических соборов, и способствовала появлению в них витража. Особое место арочный пролет занимает в мостострое, ведь именно благодаря этому элементу было создано огромное количество переправ. Сейчас же при помощи арочного принципа можно с легкостью создать покрытия промышленных, сельскохозяйственных и общественных зданий пролетом от 12 до 100м. Это могут быть ангары и складские помещения, спортивные и торговые комплексы, различные кровельные системы. Виды и формы арок, их назначение, а так же сооружение, в которых они применяются, достигли необыкновенного разнообразия и, скорее всего, пришли к кульминационному моменту развития, продолжая свой длинный исторический путь.

Происхождение и природа арок

Как же человек пришел к такой несокрушимой и долговечной конструкции, которую легко соорудить из природных материалов, создав прочную опору для всего сооружения?

Скорее всего, люди заметили эту форму в природе, окружающей человека испокон веков. Арки были всегда на виду у человека – это и вход в пещеру, и грот, и склоненные друг к другу деревья, и радуга, и полукруг заходящего солнца. В мире встречаются необычные и причудливые природные арки. Они разбросаны по свету и присутствуют на каждом материке. Эти гигантские естественные шедевры вырезаны из твердых скал, под влиянием воды, ветра и солнца.

Некоторые из них возвышаются на десятки метров над землей, в то время как другие едва сформированы и почти незаметны, но в любом случае их объединяет одно – все эти красивые естественные формирования обладают уникальной формой арки. Примеров таких явлений бесконечное множество, так что придется привести лишь наиболее монументальные и известные арки. Это Лондонская арка на побережье южной Австралии, гора Слоновий хобот, расположенная на побережье реки в южном Китае, утес Персе в Квебеке в восточной Канаде, Дердл-Дор – выступ на северном побережье Великобритании, Лазурное Око на западном побережье мальтийских островов. Радужный мост и Изящная арка находятся в США в штате Юта, где располагается целый национальный парк арок. В парке находится более 2000 природных арок из песчаника, а так же множество других ландшафтных образований. Он имеет площадь 309 кв. км и находится неподалеку от города Моаб. А самой большой на данный момент считается арка, расположенная в Китае, – мост Фей, пролет которой около 120 метров. Подобные, сформированные природой, арки можно встретить и в России: гора Кольцо в окрестностях Кисловодска, грот Дианы в мысе Лермонтова, Арка Стеллера на дальневосточном побережье, скала Золотые ворота близ массива Кара-Даг и др.

У людей первобытного мира арка принимала участие в ритуалах и, скорее, служила символом, в который вложен особый смысл, ведь через нее можно пройти. Например, у некоторых племен центральной Африки существует обряд, согласно которому, что бы мальчик стал мужчиной, он должен на несколько дней отправиться в лес и выжить там. Племя строит из веток арку на окраине леса, юноши, которые должны доказать, что уже готовы повзрослеть, уходят через арку в чащу, а оставшееся в деревне племя, начинает их оплакивать. Когда же те вернуться, то считаются уже зрелыми и готовыми к жизни мужчинами. Так же, пигмеи верят в существование бога радуги и, когда она, наконец, появляется, они, выражая желание общаться с ним, берут лук и стреляют в радугу. У римлян, где богом ворот и дверей был двуликий Янус, проход через ворота, по сторонам которых находились алтари Януса и Юноны, символизировал переход из одного возраста в другой. Значение ворот в религии Древнего Рима не ограничивалось обрядом юношеской инициации, но также было своеобразным способом очищения от зла. Арка была символом небосвода, у греков она обозначала Зевса, у римлян – Юпитера, а 35 арок символизировали дорогу жизни. Арки участвовали и в ритуале чествования и освящения победы. Триумфальные арки в конце концов наводнили всю Италию. Они были символом, увековечивающим победы. Однопролетные, глубокие, массивные арки на Руси были городскими воротами, защищающими от врагов, но в мирное время служили точкой отправления ритуальных шествий, так например, у главных ворот встречали масленицу и поедали блины. Дуга была и обтекаемым, динамичным элементом, присутствуя в конской упряжке. Важным является присутствие арки в обряде кумования на троицу. По обычаю, нужно сплести верхушки двух молодых, стоящих рядом берез, и, пройдя через получившуюся арку, обняться и поцеловаться – покумоваться. После этого девушки становились неразлучными подругами, и их не должны были посещать ссоры. Таким образом, арка, как символ, элемент быта, инструмент обрядов присутствует у различных народов и цивилизаций и играет важную роль в их жизни и культуре.

Физические свойства

Распределение сил

Суть работы арки можно представить на следующем простом примере: любая прямолинейная балка под воздействием нагрузки будет прогибаться. Происходит это потому, что под действием нагрузки в поперечных сечениях балки возникают продольные сжимающие и растягивающие напряжения. При этом в верхней части сечения действуют сжимающие напряжения, а в нижней части – растягивающие напряжения. Под действием этих напряжений верхняя часть балки сжимается, а нижняя – растягивается. В итоге, после прогиба балки, получается как бы перевернутая арка. Но если взять балку, уже имеющую некоторую кривизну оси, относительно большую по сравнению с пролетом, и перевернуть ее, то мы получим нечто, напоминающее арку. Такая теория касается арок, выполненных из цельного пласта материала. Совершенно другая идея лежит в основе арок, собранных из отдельных элементов, чаще всего, каменных. Сегменты выточены в виде усеченных клиньев, так что, опираясь друг на друга, они последовательно предают нагрузку, идущую сверху, соседнему сегменту, пока та вся не перейдет в опоры. Так что, если материал арки и опор имеет соответствующую прочность, то при повышении нагрузки арка лишь становится плотнее и крепче, это увеличивает срок ее службы и улучшает устойчивость.

Расчет арок

Расчет арок производится по правилам строительной механики. Начинают с замера и учета всех нагрузок, таких как масса самой арки, снеговая и ветровая нагрузки, а также прочие нагрузки, связанные с использованием помещения. После чего можно переходить к расчетам, которые выполняются в следующем порядке:

геометрический расчет арки;
статический расчет;
подбор сечений и проверка напряжений;
расчет узлов арки.

Нагрузки

Приходится учитывать, что нагрузки, действующие на арку, могут распространяться равномерно, на всю площадь поверхности, а могут быть сосредоточенны в отдельных местах. Например, точно постоянной и равномерной нагрузкой можно считать давление от массы покрытия и самой арки. К ним чаще всего добавляют условно полученный запас прочности, равномерно распределенной по длине пролета. Для определения массы арки используют коэффициенты собственной массы kсв = 2…4, который зависит от массы покрытия gn, снега p, других нагрузок и присутствует в выражении

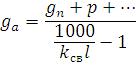
Снеговую нагрузку р так же условно считают равномерно распределенной по длине пролета покрытия и определяют по нормам нагрузок и воздействий. Стрельчатые арки в этом случае принимают за треугольные, а для сегментных арок вводят определенные коэффициенты. Ветровую нагрузку q и считают приложенной нормально к поверхности покрытия и определяют так же по нормам нагрузок и воздействий. При этом для упрощения расчета криволинейные эпюры этой нагрузки можно заменять прямолинейными, а стрельчатые так же заменяют треугольными. Сосредоточенные, временные нагрузки Р включают в себя массу подвесного оборудования, или оборудования, находящегося на покровах пролета, и временных нагрузок на нем.

Геометрический расчет арки

Он заключается в определении всех размеров, углов и их тригонометрических функций полуарки, необходимых для дальнейших расчетов. Исходными данными при этом являются пролет l, высота f, а в стрельчатых арках также радиус полуарки r или ее высота f.

Статический расчет

Если рассматривать трехшарнирную арку, то опорные реакции состоят из вертикальных и горизонтальных составляющих. Причем вертикальные реакции определяют так же, как в свободно опертой балке, из условия равенства нулю моментов в опорных шарнирах. Горизонтальные реакции, которые называют распором, определяют из условия равенства моментов нулю в коньковом шарнире. Продольные и поперечные силы можно определять только в сечениях у шарниров, где они достигают максимальных величин, что необходимо для расчетов узлов. Полученные результаты сводят в таблицу усилий, по которой затем определяют максимальные расчетные усилия при основных наиболее не выгодных сочетаниях нагрузок.

Подбор сечений и проверка напряжений производятся по максимальным значениям расчетных усилий. При этом ветровые нагрузки учитываются только в тех случаях, если ветер более чем на 20% увеличивает расчетные усилия. Так же производится ряд проверок, на прочность, устойчивость к деформациям.

После глобальных расчетов выполняется анализ узлов арки, как опорных, так и замковых, если они есть. Производится проверка узла на смятие и устойчивость к горизонтальным нагрузкам.

[spoiler title=”источники:”]

http://tarologiay.ru/nauka/chto-takoe-horda-okruzhnosti-v-geometrii-eyo-opredelenie-i-svoystva.html

http://www.krugosvet.ru/enc/arkhitektura/arochnye-konstruktsii

[/spoiler]

CHELZabor.ru

ЧелЗабор | Металлоконструкции для дома и дачи

+7 (951) 81-888-77

E-mail: info@chelzabor.ru

Собираемся сделать арку между гостиной и детской комнатами – муж хочет сам произвести расчеты, посоветуйте, как это сделать? Рассчет арки, а точнее ее изгиба, вопрос вкуса, главное рассчитать центральную точку и отталкиваясь от нее ровно вырезать полукруг. Для этого потребуется измерить ширину и высоту арки, а также определиться с высотой закругления. Стоит учитывать, что закругление не должно сильно возвышаться над дверями (если таковые имеются в одном помещении с аркой), так как арка будет казаться слишком высокой. Если Вам необходим идеальный полукруг, то можно в центральную точку закрутить саморез, а далее при помощи веревочки/ниточки и карандаша,очертить полукруг. Иначе, понадобится какая-нибудь гибкая планка, например, порожек или что-то подобное, главное, чтобы он легко гнулся, но при этом сохранял форму за счет своей упругости. Прикладываем, изгибаем и прочерчиваем. Вырезаем при помощи ножа или электролобзика. Вот и все, шаблон готов. система выбрала этот ответ лучшим домов­ой [31.4K] 7 лет назад Что вы имели ввиду под расчётом арки непонятно, но скорее всего имели ввиду рассчитать какой сделать изгиб, это дело лично каждого и его удобства, но изгиб не должен мешать удобному и беспрепятсвенному проходу людей, если вы занизите края арки то, проход будет возможен только в средней части проёма, а это уже решать вам устраивает вас это или нет – возможно устраивает. Поэтому вначале нужно определится на какой высоте проёма будут находится края арки и отметить их на стенах или проёме, допустим это высота 1.70 метра, вот вам и первый расчёт. Далее нужно определить центр проёма на высоте и уже от него делать изгиб самой арки, в каждом случае он получится разный в зависимости от самой высоты и ширины проёма, в любом случае вы можете только регулировать высоту краёв изменяя угол окружности, больше ничего. Пусть возьмут пластиковую панель, она достаточно легко гнётся и просто методом подбора, найдут оптимальный вариант, ничего сложного в расчёте арки нет, тем более декоративной, это не свод моста, тут учёным быть не нужно! Вот некоторые размеры и расчёты арок. Ким Чен Ын [489K] 6 лет назад Арки сами по себе разные, не только по типу конструкции, но и по материалу изготовления. Методы расчётов так же не одинаковые, можно пойти математическим путём и рассчитать арку с использованием математических формул, можно всё сделать гораздо проще, то есть абсолютно практические расчёты. Измеряем дверной проём где будет арка (длина, ширина, высота). Переносим все размеры на лист бумаги, но сразу же определяемся с точным масштабом, то есть на бумаге должен быть выдержанный в определённом масштабе чертеж. Чертим проём (см. выше о масштабе). Делим его строго пополам, линией, по ширине и длине. В этой точке ставим ножку циркуля и чертим дугу, если дуга не понравилась (другой радиус интересует) можно начертить несколько дуг и остановиться на понравившейся, остальные стереть ластиком. Всё, арка готова, осталось перенести размеры в реальном масштабе, сделать шаблон и так далее. Можно воспользоваться и специальными программами расчёта арок. Вам в помощь будет простейшая геометрическая формула, в которой вы исходя из высоты предполагаемой дуги (на картинке под обозначением h) и длины хорды, а по сути ширины пролёта без отделки (на картинке под обозначением a), высчитываете радиус (на картинке под обозначением R) и если нужно, то длину хорды (на картинке под обозначением b). Можно пойти от обратного, если у вас есть готовая арка и вам нужно рассчитать какой проём нужно вырезать, то получается от радиуса арки и высоты дуги вы можете высчитать ширину проёма и гипотенузу. Для этой цели можно воспользоваться программой “PowerArch”, она хоть и платная, но есть ознакомительная версия, которой вам хватит для расчёта одной арки. очУме­лый Флами­нго [8.3K] 8 лет назад При расчете каждой детали для арки, делайте их немного больше, чем по чертежу, так как детали будут накладываться друг на друга, стыковаться. Среднестатистическая ориентировка на высоту арки – 10 процентов ширины двери над ее проемом. Радиус арки удобнее рассчитать при помощи школьной формулы: R = (L+H) / 2H. Н – высота арки от точки L. L – центр ширины, расстояние до центра ширины арки от края к середине, точка L делит всю ширину ровно пополам. R – радиус арки. Сначала измеряется ширина будущей арки, этот показатель делят пополам, центр будет точкой отсчета, обозначенный буквой L. Высота арки и радиус не всегда совпадают, поэтому их определяют по отдельности, высоту можно сразу вычислить, если соединить центр ширины и максимально высокую точку, а радиус находят по заданной формуле. Прежде, чем делать арку из дерева и досок, следует изготовить шаблон из картона или бумаги, чтобы быть уверенным в правильности проведенных расчетов. Можно делать арку без расчетов, подбирать высоту на свое усмотрение, но тогда следует добавить 5 сантиметров для проема арки, который будет накладывать поверх дверного проема для фиксации. Знаете ответ?

---